多项式小记
基本介绍
多项式,听起来非常抽象的东西,的确,这个东西是一个省选的知识点,所以它确实不简单。但是随着算法学习的深入,它也显得非常重要。其主要功能,或者说其中包含算法的主要功能主要是更高效率的进行一些多项式的计算,其中的一些思想可以说是极为优美。
FFT
前置芝士
- \(F(x)\)表示多项式\(F\),例如\(A(x)\)可以为\(x^2+3x+2\)
- 系数表示法:一般来说,我们表示多项式用的都是系数表示法。比如对于上面的\(A(x)\),我们可以用数组\([1,3,2]\)来表示它每一项的系数,简单明了
- 系数表示法计算乘积:在系数表示发的情况下,如何计算多项式的乘积?非常简单,若\(C(x)=A(x)\times B(x)\)则\(C[k]=\sum_{i=0}^{k}A[i]\times B[k-i]\),假设\(A\)有\(n\)项,\(B\)有\(m\)项,则计算的时间复杂度就是\(O(nm)\)的
DFT(IDFT)思想
为了加速计算过程,我们首先从表示方法考虑。有没有其他可以表示多项式的方法?
是有的。考虑一个一次函数,我们知道其图像一定是一个直线,我们知道两点确定一个直线,因此我们可以用两个点来表示一个一次函数。
把这个结论推广(可以去思考更详细的证明),我们可以知道\((d+1)\)个不同点可以确定一个\(d\)次的多项式。
所以对于\(F(x)\)我们可以用\((x_0,F(x_0)),...,(x_n,F(x_n))\)来表示
这样子我们会发现,我们再次计算\(A(x)\times B(x)\)的时候,我们知道\(C\)至多有\(mn\)项,因此我们在\(A,B\)中用\(mn+1\)个不同的值计算出其对应的函数值,相乘,就可以得到\(C\)里面所有这些值对应的函数值,之后可以反推出来\(C\)的表达式。
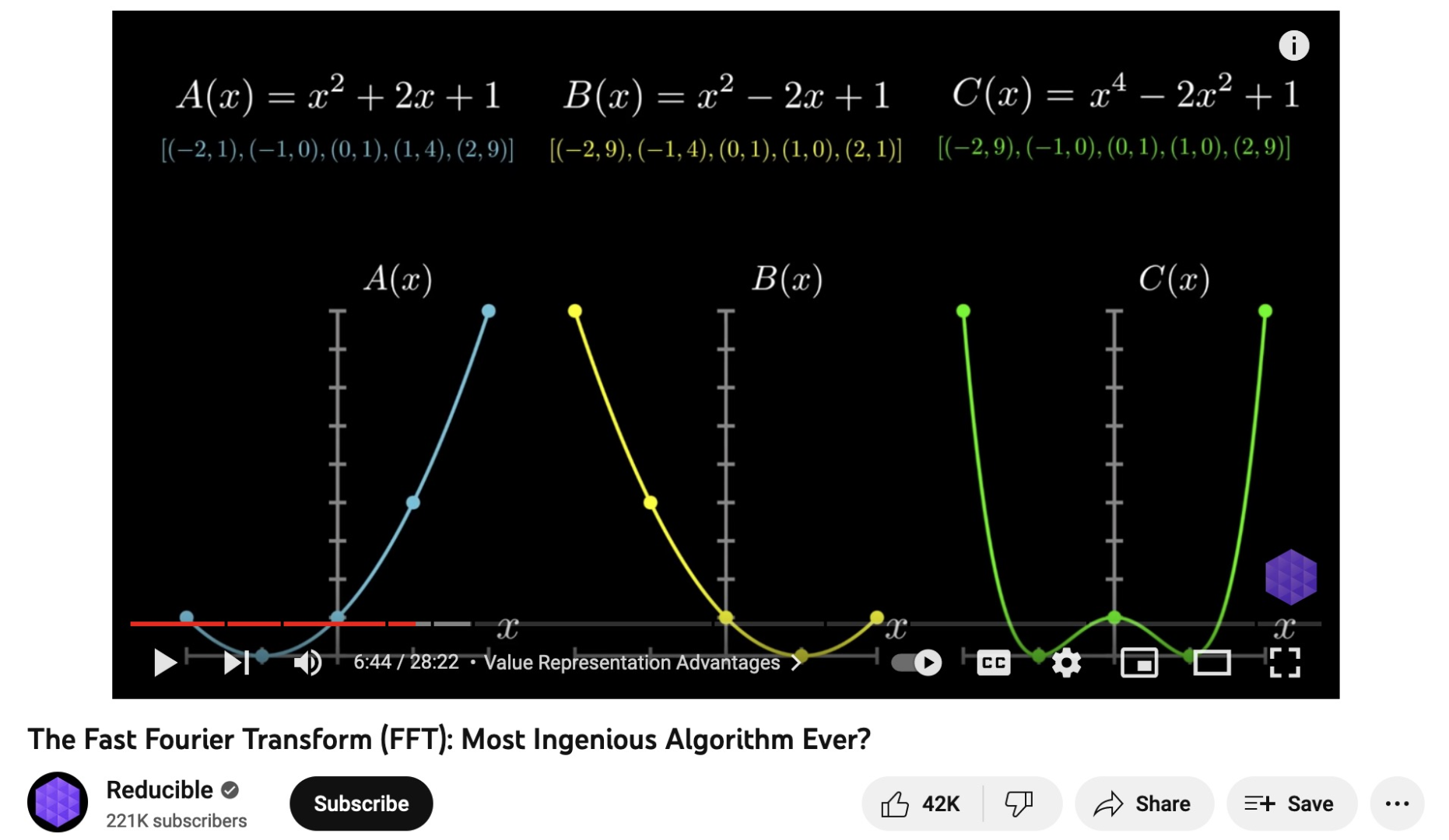
这样我们就会发现,时间复杂度就会变成了\(O(max(m,n))\)
但是问题是,如何把系数表达式,化为点表达式?
如果随机取点,我们需要取\(\ge n+1\)个点,会发现复杂度是\(O(nd)\)回到原点。
系数\(\to\)点,FFT
思考\(F(x)=x^2\),我们发现其一个性质\(F(-x)=F(x)\),这样我们我们是不是只需要取\(\dfrac{n}{2}\)个点?
思考\(F(x)=x^3\),有\(F(-x)=-F(x)\),是不是也是只需要\(\dfrac{n}{2}\)个点?
浅浅推广一些,我们假设\(F_e(x),F_o(x)\)分别表示一个函数当中所以偶数和奇数项之和,他们的系数依赖于\(F(x)\),比如说\(F_e(x)=F[0]+F[2]x+...+F[n-2]x^{n/2-1}\)
我们会有以下两个式子:\(F(x)=F_e(x^2)+xF_o(x^2)\)和\(F(-x)=F_e(x^2)-xF_o(x^2)\)
有这样一个公式,我们发现我们通过一个递归,但是一个小问题仍然存在
就是我们开始的\([\pm x_1,...,\pm x_{n/2}]\)是正负匹配的,
这里的愿意就是只要我们知道\(x_1\),我们就知道了\(-x_1\),两个值
但是我们分成一半之后,会发现\([x_1^2,...,x_{n/2}^{2}]\)不是正负匹配的了,我们就会去计算全部正数的一些值,无法一次求两个,如何解决?
那么如何做到可以继续正负匹配?
这里我们就考虑到虚数了!
假设我们现在有\([x_1,-x_1,x_2,-x_2]\),那么平方之后就会有\([x_1^2,x_2^2]\),我们希望这两个是正负相反的,因此我们希望得到的是\([x_1^2,-x_1^2]\),再进一步,最后我们到到的是\(x_1^4\)。
我们假设\(x_1=1\),我们解一下会发现最后\(x_1^4=1\),且原始的四个数字分别是\([1,-1,i,-i]\),这四个数字被称为4的单位根。即满足\(x^4=1\)的所有解。
我们思考并推广一下。对于一个\(m\)次的多项式,我们找到满足$n\ge m,n=x^k,k\in \mathbb{Z} $,之后求其单位根,代入九个得到合适的答案。
单位根有个小性质,其所有点在复平面中单位圆上,且刚好把这个单位圆分成\(n\)等分。
继续推理完善,我们假设\(\omega_{i}^{j}\)表示\(i\)的\(j+1\)个单位根,从\((1,0)\)逆时针标号。
对于它,有几个点:
- \(\omega_{n}^{k}\)可以理解为把(1,0)绕原点旋转\(\dfrac{k}{n}\)个圆周得到的点
- \(\omega_{n}^{k}=\omega_{pn}^{pk}\),也就是把这个圆分成一定份数去某一份,将这个过程翻个倍,不会影响
- \(\omega_{n}^{j}\times \omega_{n}^{k}=\omega_{n}^{jk}\)
- 若\(n\)是2的倍数,\(\omega_{n}^{k+n/2}=-\omega_{n}^{k}\)
我们代入一下分析:
Case 1:
\(F(x)=F_e(x^2)+xF_o(x^2)\)
经过一些化简可以得到:
\(F(\omega_{n}^{k})=F_e(\omega_{n}^{2k})+\omega_{n}^{k}F_o(\omega_{n}^{2k})\)
Case 2:
\(F(-x)=F_e(x^2)-xF_o(x^2)\)
经过一些化简可以得到:
\(F(-\omega_{n}^{k})=F_e(\omega_{n}^{2k})+\omega_{n}^{k}F_o({\omega_{n}^{2k}})\)
更好的操作
我们把上面的式子转换一下,变成这样子会好做一点(因为上面的\(2k\)可能会超过\(n\),代码做不到极简,当上面的写法也是完全没有问题的)
\(F(ω^{k+n/2}_n)=FL(ω^{k}_{n/2})-ω^k_nFR(ω^{k}_{n/2})\)
\(F(ω^k_n)=FL(ω^k_{n/2})+ω^k_nFR(ω^k_{n/2})\)
这意味着什么?这意味着知道后面两个值的情况我们可以\(O(n)\)求出来\(F\)的值了!
最后,我们再考虑\(\omega\)怎么求。这里运用一点非常非常基础的三角函数的值就知道\(\omega_n^1=(\cos \dfrac{2\pi}{n},\sin \dfrac{2\pi}{n})\)
于是乎,经过我们这样简单的操作,我们就做到了能够\(O(nlogn)\)做到系数\(\to\)点
系数\(\gets\)点
最后反推的过程,这里有一个结论就是把上面的\(\sin \dfrac{2\pi}{n}\)换成\(-\sin \dfrac{2\pi}{n}\)就可以啦!这里也可以通过推理\(\omega\)得出来,这里不太多赘述,只要理解上面的部分,下面也就基本可以理解了。
总结
到此为止,FFT的基本流程就掌握啦!非常值得回味,这确实是一个极为精妙的算法。
标签:系数,dfrac,可以,多项式,omega,我们,小记 From: https://www.cnblogs.com/Jryno1-blog/p/16966982.html