\({\color{Red}{欢迎到学科网下载资料学习 }}\)
[ 【基础过关系列】高二数学同步精品讲义与分层练习(人教A版2019)]
( https://www.zxxk.com/docpack/2875423.html)
\({\color{Red}{ 跟贵哥学数学,so \quad easy!}}\)
选择性第二册同步巩固,难度2颗星!
基础知识
数列的概念
(1)定义:数列是按照一定次序排列的一列数;
(2)数列的项:数列中的每一个数叫做这个数列的项,第一项常称为首项;
(3)数列的表示:数列的一般形式可以写成\(a_1\),\(a_2\),… ,\(a_n\),…,简记\(\{a_n\}\).
解释
与集合中元素的性质相比较,数列中的项也有三个性质:
①确定性:一个数在不在数列中,即一个数是不是数列中的项是确定的.(与集合相同)
②可重复性:数列中的数可以重复.(与集合不同)如数列\(1\),\(1\),\(1\),而由\(1\),\(1\),\(1\)组成的集合是\(\{1\}\).
③有序性:一个数列不仅与构成数列的“数”有关,而且与这些数的排列次序有关.(与集合不同)如\(1\),\(3\),\(4\)与\(1\),\(4\),\(3\)代表不同的数列,而集合\(\{1,3,4\}\)与\(\{1,4,3\}\)却是相同的.
【例】下列说法错误的是( )
A.数列\(4,7,3,4\)的首项是\(4\)
B.数列\(\{a_n \}\)中,若\(a_1=3\),则从第\(2\)项起,各项均不等于\(3\)
C.数列\(-1,0,1,2\)与数列\(0,1,2,-1\)不相同
D.数列\(\{2n-1\}\)的第\(k\)项\(a_k=2k-1\)
答案 \(B\)width:1000px;
数列的分类
| 分类标准 | 名称 | 含义 | 例子 |
| 按项的个数 | 有穷数列 | 项数有限的数列 | $1 ,2 ,3 ,4 ,….,n$ |
| 无穷数列 | 项数无限的数列 | $1 ,2 ,3 ,4 ,… ,n ,….$ | |
| 按项的大小 | 递增数列 | $a_n>a_{n-1} (n≥2)$ | $2 ,4 ,8 ,… ,2n ,…$ |
| 递减数列 | $a_n < a_{n-1} (n≥2)$ | $1, \dfrac{1}{2}, \dfrac{1}{3}, \ldots, \dfrac{1}{n}, \ldots$ | |
| 常数列 | 每项都相等的数列 | $1 ,1 ,1 ,…$ | |
| 摆动数列 | 每项的大小忽大忽小的数列 | $1 ,-2 ,3 ,-4 ,5 ,…$ |
【例】判断以下数列的类型
(1) \(2,4,8,16,…,2^n\); \(\qquad \qquad\) (2) \(\dfrac{1}{2}, \dfrac{1}{4}, \dfrac{1}{8}, \dfrac{1}{16}, \ldots, \dfrac{1}{2^n},\);\(\qquad \qquad\) (3)\(a,a,a,a,…\)
答案 (1)递增数列,有穷数列;(2)递减数列,无穷数列;(3)常数列,无穷数列
通项公式
如果数列\(\{a_n\}\)的第\(n\)项与序号\(n\)之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式.
解释
(1)\(a_n\)与\(\{a_n\}\)是不同的概念,\(\{a_n\}\)表示数列\(a_1\) ,\(a_2\),⋯,而\(a_n\)表示的是数列的第\(n\)项;
(2)数列的项与它的项数是不同的概念,数列的项是指这个数列中的某一个确定的数,它是一个函数值;而项数是指这个数在数列中的位置序号,它是自变量的值.
(3)一个数列的通项公式可以有不同的形式,比如数列\(1 ,0 ,1 ,0,…\),其通项公式可以是 \(\dfrac{1+(-1)^{n+1}}{2}\) , \(a_n=\sin ^2 \dfrac{n \pi}{2}\)等.
【例1】已知数列\(1,2,3,4,…\),则这个数列的一个通项公式是( )
A.\(a_n=1\) \(\qquad \qquad \qquad \qquad\) B.\(a_n=n^2\) \(\qquad \qquad \qquad \qquad\) C.\(a_n=n\) \(\qquad \qquad \qquad \qquad\) D. \(a_n=\sqrt{n}\)
答案 \(C\)
【例2】数列\(\{a_n\}\)中,\(a_n=3^n+n-1\),则\(a_2\)等于 .
答案 \(10\)
数列与函数的关系
数列就是定义在正整数集\(N^*\)(或它的有限子集\(\{1 ,2 ,3....n\})\)上的函数\(f(n)\),其图象是一系列有限或无限孤立的点.
如
数列\(a_n=n^2\)与函数\(y=x^2\)的比较
| \(a_n=n^2\) | \(y=x^2\) | |
|---|---|---|
| 定义域 | \(N^*\) | \(R\) |
| 图象 | 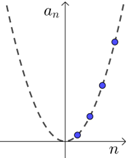 |
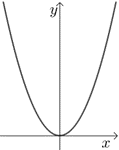 |
| 增减性 | 递增数列 | 在\((-∞,0)\)递减 |
| 在\((0,+∞)\)递增 | ||
| 最值 | 最小项\(1\),无最大项 | 最小值\(0\),无最大值 |
日后研究数列性质可以从函数角度出发,比如单调性,最值等.
基本方法
【题型1】数列的概念
【典题1】 下列叙述正确的是( )
A.数列\(1,3,5,7\)与\(7,5,3,1\)是同一数列 \(\qquad \qquad \qquad \qquad\) B.数列\(0,1,2,3,…\)的通项公式是\(a_n=n\)
C.\(-1,1,-1,1,…\)是常数列 \(\qquad \qquad \qquad \qquad\) D.\(1,2,2^2,2^3,…\)是递增数列,也是无穷数列
解析 根据题意,依次分析选项:
对于\(A\)、数列\(1,3,5,7\)与数列\(7,5,3,1\)中顺序不同,不是同一数列,故\(A\)错误;
对于\(B\)、数列\(0,1,2,3,…\)的通项公式是\(a_n=n-1\),故\(B\)错误;
对于\(C\)、常数列的通项为\(a_n=a\),则\(-1,1,-1,1,…\)不是常数列,故\(C\)错误;
对于\(D\)、\(1,2,2^2,2^3,…\)是递增数列,也是无穷数列,故\(D\)正确.
故选:\(D\).
【巩固练习】
1.下列说法不正确的是( )
A.数列不一定有通项公式 \(\qquad \qquad \qquad \qquad\) B.数列的通项公式不一定唯一
C.数列可以用一群孤立的点表示 \(\qquad \qquad \qquad \qquad\) D.数列的项不能相等
2.下列说法正确的是( )
A.数列\(1,-2,3,-4,…\)是一个摆动数列 \(\qquad \qquad \qquad \qquad\) B.数列\(-2,3,6,8\)可以表示为\(\{-2,3,6,8\}\)
C.\(\{a_n\}\)和\(a_n\)是相同的概念 \(\qquad \qquad \qquad \qquad\) D.每一个数列的通项公式都是唯一确定的
参考答案
-
答案 \(D\)
解析 根据题意,依次分析选项:
对于\(A\),数列不一定有通项公式,如某班级每天消耗的文具数量,\(A\)正确;
对于\(B\),数列的通项公式可以有多个,不一定唯一,\(B\)正确;
对于\(C\),数列中n为正整数,可以用一群孤立的点表示,\(C\)正确;
对于\(D\),数列的项的可以相等,\(D\)错误;
故选:\(D\). -
答案 \(A\)
解析 根据摆动数列的概念,\(A\)正确;
数列\(-2,3,6,8\) 不能表示为集合\(\{-2,3,6,8\}\),
数列和元素顺序有关,集合和元素顺序无关,故\(B\)错误.
\(\{a_n\}\)表示数列的全部的项,而\(a_n\)表示数列的第\(n\)项,不是同一概念,故\(C\)错;
数列的通项公式可以有多个,\(D\)错误.
故选:\(A\).
【题型2】 根据数列的前几项写出数列的一个通项公式
【典题1】 写出下列数列\(\{a_n\}\)的一个通项公式:
(1)\(-7 ,14 ,-21 ,28,…\); \(\qquad \qquad\) (2) \(\dfrac{1}{4}, \dfrac{3}{8}, \dfrac{5}{16}, \dfrac{7}{32} \ldots\);
(3)\(2 ,5 ,10 ,17 ,26 ,…\); \(\qquad \qquad\) (4)\(2 ,32 ,332 ,3332 ,33332 ,….\)
解析 分解结构法
(1) 数列\(-7 ,14 ,-21 ,28,…\)每项可分解成符号和项的绝对值相乘得到,
| 序号 | \(1\) | \(2\) | \(3\) | \(4\) | \(……\) | \(n\) |
|---|---|---|---|---|---|---|
| 符号 | \(-\) | \(+\) | \(-\) | \(+\) | \((-1)^n\) | |
| 绝对值 | \(7\) | \(14\) | \(21\) | \(28\) | \(7n\) | |
| 项 | \((-1)^n 7n\) |
故\(a_n=(-1)^n 7n\);(奇偶性的符号变换规律可考虑\((-1)^n\)或\((-1)^{n-1}\)).
(2) 数列 \(\dfrac{1}{4}, \dfrac{3}{8}, \dfrac{5}{16}, \dfrac{7}{32} \ldots\)每项可分解成分子和分母相除得到,
| 序号 | \(1\) | \(2\) | \(3\) | \(4\) | \(……\) | \(n\) |
|---|---|---|---|---|---|---|
| 分子 | \(1\) | \(3\) | \(5\) | \(7\) | \(2n-1\) | |
| 绝对值 | \(4\) | \(8\) | \(61\) | \(32\) | \(2^{n+1}\) | |
| 项 | \((2n-1)2^{n+1}\) |
(分子相邻数之间的差是\(2\),是等差数列;分母相邻数之间是\(2\)倍的关系,是等比数列)
故\(a_n=(2n-1)2^{n+1}\).
变形法
(3)数列\(2 ,5 ,10 ,17 ,26 ,…\)中若每项减去\(1\),则变成\(1 ,4 ,9 ,16 ,25 ,…\),
这些数都是完全平方数,易想到数列的通项是\(n^2\),
则原数列只需要在这基础上加回\(1\)便可,即\(a_n=n^2+1\).
(4)数列\(2 ,32 ,332 ,3332 ,33332 ,….\)中若每项加上\(1\),
则变成\(3 ,33 ,333 ,3333 ,33333 ,…\),
再每项乘以\(3\),变成\(9 ,99 ,999 ,9999 ,99999 ,…\)
其中\(9=10-1\),\(99=10^2-1\),\(999=10^3-1\),\(9999=10^4-1\),\(99999=10^5-1\),
则其通项\(b_n=10^{n+1}-1\),
要求原数列的通项公式,
则“逆回去”,除以\(3\)再减\(1\)可得 \(a_n=\dfrac{b_n}{3}-1=\dfrac{10^{n+1}-1}{3}-1=\dfrac{10^{n+1}-4}{3}\).
【巩固练习】
1.下列可作为数列\(1,2,1,2,1,2,…\)的通项公式的是( )
A. \(a_n=\dfrac{1+(-1)^{n-1}}{2}\) \(\qquad \qquad \qquad \qquad\) B. \(a_n=\dfrac{3+(-1)^n}{2}\) \(\qquad \qquad \qquad \qquad\) C. \(a_n=2-\sin \dfrac{n \pi}{2}\) \(\qquad \qquad \qquad \qquad\) D. \(a_n=2-\cos [(n-1) \pi]\)
2.写出下面各数列的一个通项公式,使它的前4项分别是下列各数:
(1) \(7,14,21,28\); \(\qquad \qquad\) (2) \(\dfrac{1}{4}, \dfrac{3}{8}, \dfrac{5}{16}, \dfrac{7}{32}\);
(3) \(\dfrac{5}{2}, \dfrac{8}{3}, \dfrac{11}{4}, \dfrac{14}{5}\); \(\qquad \qquad\) (4) \(1 \dfrac{1}{2},-3 \dfrac{1}{4}, 5 \dfrac{1}{8},-7 \dfrac{1}{16}\);
参考答案
-
答案 \(B\)
解析 根据题意,数列\(1,2,1,2,1,2,…\)
其奇数项为\(1\),可以看作 \(\dfrac{3+(-1)}{2}\),偶数项为\(2\),可以看作 \(\dfrac{3-(-1)}{2}\);
其通项公式可以为: \(a_n=\dfrac{3+(-1)^n}{2}\);
故选:\(B\). -
答案 (1)\(a_n=7n\);(2) \(a_n=\dfrac{2 n-1}{2^{n+1}}\) ;(3) \(a_n=\dfrac{3 n+2}{n+1}\);(4) \(a_n=(-1)^{n+1}\left(2 n-1+\dfrac{1}{2^n}\right)\).
解析 (1)数列\(7,7×2,7×3,7×4\),所以通项公式为\(a_n=7n\).
(2)数列 \(\dfrac{2 \times 1-1}{2^2}, \dfrac{2 \times 2-1}{2^3}, \dfrac{2 \times 3-1}{2^4}, \dfrac{2 \times 4-1}{2^5}\),所以数列通项公式为 \(a_n=\dfrac{2 n-1}{2^{n+1}}\).
(3)数列 \(1 \dfrac{3 \times 1+2}{1+1}, \dfrac{3 \times 2+2}{2+1}, \dfrac{3 \times 3+2}{3+1}, \dfrac{3 \times 4+2}{4+1}\),所以数列通项公式 \(a_n=\dfrac{3 n+2}{n+1}\).
(4)数列 \((-1)^{1+1}\left[2 \times 1-1+\dfrac{1}{2}\right]\), \((-1)^{2+1}\left[2 \times 2-1+\dfrac{1}{2^2}\right]\), \((-1)^{3+1}\left[2 \times 3-1+\dfrac{1}{2^3}\right]\), \((-1)^{4+1}\left[2 \times 4-1+\dfrac{1}{2^4}\right]\),所以数列通项公式 \(a_n=(-1)^{n+1}\left(2 n-1+\dfrac{1}{2^n}\right)\).
【题型3】 通项公式的应用
【典题1】 已知数列\(\{a_n \}\)的通项公式为\(a_n=3n^2-28n\).
(1)写出数列的第\(4\)项和第\(6\)项;
(2)\(-49\)是否是该数列的一项?如果是,是哪一项?68是否是该数列的一项呢?
解析 (1)\(a_4=3×16-28×4=-64\),\(a_6=3×36-28×6=-60\).
(2)设\(3n^2-28n=-49\),解得\(n=7\)或 \(n=\dfrac{7}{3}\)(舍去),
\(\therefore n=7\),即\(-49\)是该数列的第\(7\)项.
设\(3n^2-28n=68\),解得 \(n=\dfrac{34}{3}\)或\(n=-2\).
\(\because \dfrac{34}{3}∉N^*\),\(-2∉N^*\),\(\therefore 68\)不是该数列的项.
【巩固练习】
1.设数列 \(\sqrt{2}, \sqrt{5}, 2 \sqrt{2}, \sqrt{11}\),则 \(2\sqrt{5}\)是这个数列的( )
A.第\(6\)项 \(\qquad \qquad \qquad \qquad\) B.第\(7\)项 \(\qquad \qquad \qquad \qquad\) C.第\(8\)项 \(\qquad \qquad \qquad \qquad\) D.第\(9\)项
2.下列数列中,\(156\)是其中一项的是( )
A.\(\{n^2+1\}\) \(\qquad \qquad \qquad \qquad\) B.\(\{n^2-1\}\) \(\qquad \qquad \qquad \qquad\) C.\(\{n^2+n\}\) \(\qquad \qquad \qquad \qquad\) D.\(\{n^2+n-1\}\)
3.已知数列\(\{a_n\}\)中,\(a_n=5n-3\).
(1)求\(a_5\);(2)判断\(27\)是否为数列\(\{a_n\}\)的一项.
4.已知数列\(\{a_n\}\)的通项公式为\(a_n=\dfrac{3 n-2}{3 n+1}\).
(1)求\(a_{10}\).
(2)判断\(\dfrac{7}{10}\)是否为该数列中的项.若是,它为第几项?若不是,请说明理由.
(3)求证:\(0<a_n<1\).
参考答案
-
答案 \(B\)
-
答案 \(C\)
解析 根据题意,依次分析选项:
对于\(A\),若数列为\(\{n^2+1\}\),则有\(n^2+1=156\),无正整数解,不符合题意;
对于\(B\),若数列为\(\{n^2-1\}\),则有\(n^2-1=156\),无正整数解,不符合题意;
对于\(C\),若数列为\(\{n^2+n\}\),则有\(n^2+n=156\),解可得\(n=12\)或\(-13\)(舍),有正整数解\(n=12\),符合题意,
对于\(D\),若数列为\(\{n^2+n-1\}\),则有\(n^2+n-1=156\),无正整数解,不符合题意;
故选:\(C\). -
答案 (1) \(22\);(2) \(27\)是数列\(\{a_n\}\)的第\(6\)项.
解析 (1)\(a_5=5×5-3=22\)
(2)令\(5n-3=27\),解得\(n=6\),即\(27\)是数列\(\{a_n\}\)的第\(6\)项. -
答案 (1) \(\dfrac{28}{31}\).(2) \(\dfrac{7}{10}\)为数列\(\{a_n\}\)中的项,为第\(3\)项.(3)略.
解析 (1)解:根据题意可得 \(a_{10}=\dfrac{3 \times 10-2}{3 \times 10+1}=\dfrac{28}{31}\).
(2)解:令 \(a_n=\dfrac{7}{10}\),即 \(\dfrac{3 n-2}{3 n+1}=\dfrac{7}{10}\),解得\(n=3\),
\(\therefore \dfrac{7}{10}\)为数列\(\{a_n\}\)中的项,为第\(3\)项.
(3)证明:由题知 \(a_n=\dfrac{3 n-2}{3 n+1}=1-\dfrac{3}{3 n+1}\),
\(\because n∈N^*\), \(\therefore 0<\dfrac{3}{3 n+1}<1\),
\(\therefore 3n+1>3\),即\(0<a_n<1\).
【题型4】 数列与函数的关系
【典题1】 数列 \(\left\{\dfrac{n}{n+2}\right\}\)是增数列还是减数列?
解析 方法1 作差法
\(a_{n+1}-a_n=\dfrac{n+1}{n+3}-\dfrac{n}{n+2}=\dfrac{2}{(n+3)(n+2)}>0\),所以 \(a_{n+1}>a_n\),
故数列 \(\left\{\dfrac{n}{n+2}\right\}\)是增数列.
方法2 作商法
\(\dfrac{a_{n+1}}{a_n}=\dfrac{n+1}{n+3} \cdot \dfrac{n+2}{n}=\dfrac{n^2+3 n+2}{n^2+3 n}>1\),
又\(\because a_n>0\),所以 \(a_{n+1}>a_n\),故数列 \(\left\{\dfrac{n}{n+2}\right\}\)是增数列.
方法3 函数法
\(a_n=\dfrac{n}{n+2}=\dfrac{1}{1+\dfrac{2}{n}}\),
\(\because f(x)=\dfrac{1}{1+\dfrac{2}{x}}\)在\((0,+∞)\)递增, \(\therefore a_n=\dfrac{1}{1+\dfrac{2}{n}}\)也是随着\(n\)的增大而增大,
故数列\(\left\{\dfrac{n}{n+2}\right\}\)是增数列.
点拨 求证数列单调性,常用方法有三:
① 作差法,比较\(a_{n+1}-a_n\)与\(0\)的大小;
② 作商法,比较\(\dfrac{a_{n+1}}{a_n}\)与\(1\)的大小,此时要注意\(a_n\)的正负性;
③ 视通项公式为函数解析 式,用讨论函数单调性的方法处理.
【典题2】 已知数列\(\{a_n\}\)的通项公式为\(a_n=-2n^2+λn(n∈N^*,λ∈R)\),若\(\{a_n\}\)是递减数列,则\(λ\)的取值范围为\(\underline{\quad \quad}\) .
解析 \(\because\)数列\(\{a_n\}\)是递减数列, \(\therefore a_n>a_{n+1}\),
\(\therefore -2n^2+λn>-2(n+1)^2+λ(n+1)\),解得\(λ<4n+2\),
\(\because\) 数列\(\{4n+2\}\)单调递增,\(\therefore n=1\)时取得最小值\(6\),
\(\therefore λ<6\).
【典题3】 已知数列\(\{a_n\}\)的通项公式是 \(a_n=(2 n+1)\left(\dfrac{9}{10}\right)^n\),\(n∈N^*\),则\(\{a_n\}\)中的最大项的序号是\(\underline{\quad \quad}\).
解析 方法1
\(a_{n+1}-a_n=(2 n+3)\left(\dfrac{9}{10}\right)^{n+1}-(2 n+1)\left(\dfrac{9}{10}\right)^n\)\(=\left(\dfrac{9}{10}\right)^n\left[\dfrac{9(2 n+3)}{10}-(2 n+1)\right]=\left(\dfrac{9}{10}\right)^n \dfrac{17-2 n}{10}\),
令\(a_{n+1}-a_n≥0\),即 \(\left(\dfrac{9}{10}\right)^n \dfrac{17-2 n}{10} \geq 0\),可得\(n≤8.5\).
令\(a_{n+1}-a_n≤0\),即 \(\left(\dfrac{9}{10}\right)^n \dfrac{17-2 n}{10} \leq 0\),可得\(n≥8.5\).
即当\(n<9\)时,\(\{a_n\}\)递增;\(n≥9\)时,\(\{a_n\}\)递减.
\(\therefore \{a_n\}\)中的最大项的序号是\(9\).
方法2 由 \(\left\{\begin{array}{l}
a_n \geq a_{n+1} \\
a_n \geq a_{n-1}
\end{array}\right.\)得 \(\left\{\begin{array}{l}
(2 n+1)\left(\dfrac{9}{10}\right)^n \geq(2 n+3)\left(\dfrac{9}{10}\right)^{n+1} \\
(2 n+1)\left(\dfrac{9}{10}\right)^n \geq(2 n-1)\left(\dfrac{9}{10}\right)^{n-1}
\end{array}\right.\),
解得 \(\dfrac{17}{2} \leq n \leq \dfrac{19}{2}\),
又\(\because n∈N^*\),\(\therefore n=9\),
即\(\{a_n\}\)中的最大项的序号是\(9\).
点拨 方法1利用函数的思路,求最大值先判断其单调性.
【巩固练习】
1.下列数列中,为递减数列的是( )
A.\(\{1+5^n \}\) \(\qquad \qquad \qquad \qquad\) B.\(\{-n^2+6n\}\) \(\qquad \qquad \qquad \qquad\) C.\(\{3n+6\}\) \(\qquad \qquad \qquad \qquad\) D.\(\{1-\log_2 n\}\)
2.数列\(\{a_n\}\)的通项 \(a_n=\dfrac{n}{n^2+90}\),则数列\(\{a_n\}\)中的最大值是( )
A. \(3 \sqrt{10}\) \(\qquad \qquad \qquad \qquad\) B.\(19\) \(\qquad \qquad \qquad \qquad\) C. \(\dfrac{1}{19}\) \(\qquad \qquad \qquad \qquad\) D. \(\dfrac{\sqrt{10}}{60}\)
3.求数列\(\{-2n^2+29n+3\}\)中的最大项是\(\underline{\quad \quad}\).
4.已知\(\{a_n\}\)满足\(a_n=(n-λ) 2^n (n∈N^*)\),若\(\{a_n\}\)是递增数列,则实数\(λ\)的取值范围是\(\underline{\quad \quad}\).
5.设\(a_n=n^2-2kn+6(n∈N^*,k∈R)\)
(1)证明:\(k≤1\)是\(\{a_n\}\)为递增数列的充分不必要条件;
(2)若\(∀n∈N^*\), \(\dfrac{a_n}{n} \geq 1\),求\(k\)的取值范围.
参考答案
-
答案 \(D\)
解析 根据题意,依次分析选项:
对于\(A\),对于数列\(\{1+5^n \}\),有\(a_1=1+5=6\),\(a_2=1+25=16\),
不是递减数列,不符合题意;(或由函数\(f(x)=1+5^x\)是增函数排除)
对于\(B\),对于数列\(\{-n^2+6n\}\),有\(a_1=-1+6=5\),\(a_2=-4+12=8\),
不是递减数列,不符合题意;(或由函数\(f(x)=-x^2+6x\)在\((0,3)\)上递增排除)
对于\(C\),对于数列\(\{3n+6\}\),有\(a_1=3+6=9\),\(a_2=6+6=12\),
不是递减数列,不符合题意;(或由函数\(f(x)=3x+6\)是增函数排除)
对于\(D\),对于数列\(\{1-\log_2 n\}\),有\(a_{n+1}-a_n=1-\log_2(n+1)-(1-\log_2n)=\log _2 \dfrac{n}{n+1}\),
当\(n≥1\)时,有\(a_{n+1}-a_n<0\),数列\(\{1-\log_2n\}\)是递减数列,符合题意,
(或由函数\(f(x)=1-\log_2 x\)是减函数可知)
故选:\(D\). -
答案 \(C\)
解析 \(a_n=\dfrac{n}{n^2+90}=\dfrac{1}{n+\dfrac{90}{n}}\),
\(\because f(n)=n+\dfrac{90}{n}\)在\((0,3\sqrt{10})\)上单调递减,在\((3\sqrt{10},+∞)\)上单调递增,
\(\therefore\)当\(n=9\)时,\(f(9)=9+10=19\),当\(n=10\)时,\(f(10)=9+10=19\),
即\(f(9)=f(10)\)为最小值,
此时\(a_n=\dfrac{n}{n^2+90}\)取得最大值为\(a_9=a_{10}=\dfrac{1}{19}\),
故选:\(C\). -
答案 \(108\)
解析 由已知,得\(a_n=-2 n^2+29 n+3=-2\left(n-\dfrac{29}{4}\right)^2+108 \dfrac{1}{8}\)
由于\(n∈N^*\),故当\(n\)取距离\(\dfrac{29}{4}\)最近的正整数7时,\(a_n\)取得最大值\(108\).
故数列\(\{-2n^2+29n+3\}\)中的最大项为\(a_7=108\). -
答案 \((-∞,3)\)
解析 \(\because \{a_n\}\)是递增数列,\(\therefore a_{n+1}>a_n\),
\(\therefore (n+1-λ) 2^{n+1}>(n-λ) 2^n\),化为:\(λ<n+2\),对\(∀n∈N^*\)都成立.
\(\therefore λ<3\).
故答案为:\((-∞,3)\). -
答案 (1) 略;(2) \(k≤2\).
解析 (1)证明:若\(\{a_n\}\)为递增数列,
则\(a_{n+1}-a_n=(n+1)^2-2k(n+1)+6-[n^2-2kn+6]=2n+1-2k>0\),
解得 \(k<\dfrac{2 n+1}{2}\), \(\therefore k<\dfrac{3}{2}\).
\(\therefore k≤1\)是\(\{a_n\}\)为递增数列的充分不必要条件;
(2)解:\(∀n∈N^*\),\(\dfrac{a_n}{n} \geq 1\),
\(\therefore n+\dfrac{6}{n}-2 k \geq 1\),即 \(n+\dfrac{6}{n} \geq 2 k+1\),
\(\because n+\dfrac{6}{n}≥5\),\(\therefore 2k+1≤5\),
\(\therefore k≤2\).
\(\therefore k\)的取值范围是\(k≤2\).
分层练习
【A组---基础题】
1.下列有关数列的说法正确的是( )
①数列\(1,2,3\)可以表示成\(\{1,2,3\}\);②数列\(-1,0,1\)与数列\(1,0,-1\)是同一数列;
③数列 \(\left\{\dfrac{1}{n}\right\}\)的第\(k-1\)项是 \(\dfrac{1}{k-1}\); ④数列中的每一项都与它的序号有关.
A.①② \(\qquad \qquad \qquad \qquad\) B.③④ \(\qquad \qquad \qquad \qquad\) C.①③ \(\qquad \qquad \qquad \qquad\) D.②④
2.在数列\(\{a_n\}\)中,已知\(a_n=\dfrac{n^2+n-1}{3}\),\(n∈N^*\),则\(\dfrac{19}{3}\)是数列中的第( )项,
A.\(3\) \(\qquad \qquad \qquad \qquad\) B.\(4\) \(\qquad \qquad \qquad \qquad\) C.\(5\) \(\qquad \qquad \qquad \qquad\) D.\(6\)
3.已知数列\(\{a_n\}\)中, \(a_n=\dfrac{n}{n+1}\),则\(\{a_n\}\)是( )
A.常数列 \(\qquad \qquad \qquad \qquad\) B.递减数列 \(\qquad \qquad \qquad \qquad\) C.递增数列 \(\qquad \qquad \qquad \qquad\) D.摆动数列
4.数列\(\{a_n\}\)是递增数列,则\(\{a_n\}\)的通项公式可以是下面的( )
A. \(a_n=-\dfrac{1}{n}\) \(\qquad \qquad \qquad \qquad\) B.\(a_n=n^2-3n\) \(\qquad \qquad \qquad \qquad\) C.\(a_n=2^{-n}\) \(\qquad \qquad \qquad \qquad\) D.\(a_n=(-n)^n\)
5.数列\(\left\{\dfrac{1}{2^n-2022}\right\}\)( )
A.既无最大项,又无最小项 \(\qquad \qquad \qquad \qquad\) B.有最大项,无最小项
C.无最大项,有最小项 \(\qquad \qquad \qquad \qquad\) D.既有最大项,又有最小项
6.数列\(\{a_n\}\)的通项公式是\(a_n=(n+2)\left(\dfrac{9}{10}\right)^n\),那么在此数列中( )
A.\(a_7=a_8\)最大 \(\qquad \qquad \qquad \qquad\) B .\(a_8=a_9\)最大 \(\qquad \qquad \qquad \qquad\) C.有唯一项\(a_8\)最大 \(\qquad \qquad \qquad \qquad\) D.有唯一项\(a_7\)最大
7.数列\(1,3,7,15,31,…\)的一个通项公式为\(\underline{\quad \quad}\) .
8.数列\(\sqrt{3}, \sqrt{8}, \sqrt{13}, \sqrt{18}, \cdots, 7 \sqrt{2}\)是其第\(\underline{\quad \quad}\)项.
9.数列\(\{a_n\}\)的通项\(a_n=-3n^2+2020n+1\),当\(a_n\)取最大值时,\(n=\)\(\underline{\quad \quad}\).
10.已知数列\(\{a_n\}\)是递增数列,且对于任意\(n∈N^*\),\(a_n=n^2+2λn+1\),则实数\(λ\)的取值范围是\(\underline{\quad \quad}\).
11.已知数列\(\{a_n\}\),\(a_n=n^2-pn+q\),且\(a_1=0\),\(a_2=-4\).
(1)求\(a_5\).
(2)判断\(150\)是不是该数列中的项?若是,是第几项?
12.在数列\(\{a_n\}\)中,已知 \(a_n=\dfrac{a n}{b n+1}\),且 \(a_2=\dfrac{6}{5}\),\(a_3=\dfrac{9}{7}\).
(1)求通项公式\(a_n\);(2)求证:\(\{a_n\}\)是递增数列;(3)求证: \(1 \leq a_n<\dfrac{3}{2}\).
参考答案
-
答案 \(B\)
解析 对于①,\(\{1,2,3\}\)是集合,不是数列,故选项①错误;
对于②,数列是有序的,故数列\(-1,0,1\)与数列\(1,0,-1\)是不同的数列,故选项②错误;
对于③,数列\(\left\{\dfrac{1}{n}\right\}\)的第\(k-1\)项是 \(\dfrac{1}{k-1}\),故选项③正确;
对于④,由数列的定义可知,数列中的每一项都与它的序号有关,故选项④正确.
故选:\(B\). -
答案 \(B\)
解析 根据题意,数列\(\{a_n\}\)中,已知 \(a_n=\dfrac{n^2+n-1}{3}\),
若 \(\dfrac{n^2+n-1}{3}=\dfrac{19}{3}\),即\(n^2+n-1=19\),解可得:\(n=4\)或\(-5\)(舍);
故选:\(B\). -
答案 \(C\)
-
答案 \(A\)
解析 根据题意,依次分析选项:
对于\(A\), \(a_n=-\dfrac{1}{n}\),有 \(a_n-a_{n-1}=\dfrac{1}{n-1}-\dfrac{1}{n}=\dfrac{1}{n(n-1)}\),
又由\(n≥2\),则\(a_n-a_(n-1)>0\),数列\(\{a_n\}\)是递增数列,符合题意;
对于\(B\),\(a_n=n^2-3n\),则\(a_1=1-3=-2\),\(a_2=4-6=-2\),
数列\(\{a_n\}\)不是递增数列,不符合题意;
对于\(C\),\(a_n=2^{-n}\),有 \(a_1=2^{-1}=\dfrac{1}{2}\), \(a_2=2^{-2}=\dfrac{1}{4}\),
数列\(\{a_n\}\)不是递增数列,不符合题意;
对于\(D\),\(a_n=(-n)^n\),有\(a_2=(-2)^2=4\),\(a_3=(-3)^3=-27\) ,
数列\(\{a_n\}\)不是递增数列,不符合题意;
故选:\(A\). -
答案 \(D\)
解析 \(\because 2^{10}=1024\),\(2^{11}=2048\),
\(\therefore\)根据指数函数的单调性知,\(\left\{\dfrac{1}{2^n-2022}\right\}\)在\(1≤n≤10\)时为减数列且为负,
在\(n≥11\)时为减数列且为正,
\(\therefore\)数列\(\left\{\dfrac{1}{2^n-2022}\right\}\)的最小项为第\(10\)项,最大项为\(11\)项.
故选:\(D\). -
答案 \(A\)
解析 \(a_n=(n+2)\left(\dfrac{9}{10}\right)^n\), \(a_{n+1}=(n+3)\left(\dfrac{9}{10}\right)^{n+1}\),
所以 \(\dfrac{a_{n+1}}{a_n}=\dfrac{n+3}{n+2} \cdot \dfrac{9}{10}\),
令 \(\dfrac{a_{n+1}}{a_n} \geq 1\)即 \(\dfrac{n+3}{n+2} \cdot \dfrac{9}{10} \geq 1\),解得\(n≤7\),
即\(n≤7\)时递增,\(n>7\)递减,
所以\(a_1<a_2<a_3<⋯<a_7=a_8>a_9>⋯\)
所以\(a_7=a_8\)最大.
故选:\(A\). -
答案 \(a_n=2^n-1\)
-
答案 \(20\)
解析 根据题意,数列\(\sqrt{3}, \sqrt{8}, \sqrt{13}, \sqrt{18}, \cdots, 7 \sqrt{2}\),
可写成 \(\sqrt{5-2}, \sqrt{5 \times 2-2}, \sqrt{5 \times 3-2}, \ldots \ldots, \sqrt{5 n-2}\),
对于 \(7 \sqrt{2}\),即 \(\sqrt{98}=\sqrt{5 \times 20-2}\),为该数列的第\(20\)项. -
答案 \(337\)
解析 依题意,\(a_n=-3n^2+2020n+1\),
表示抛物线\(f(n)=3n^2+2020n+1\)当\(n\)为正整数时对应的函数值,
又\(y=3n^2+2020n+1\)为开口向下的抛物线,
故到对称轴\(n=-\dfrac{2020}{2 \times(-3)}=\dfrac{1010}{3}\)距离越近的点,函数值越大,
故当\(n=337\)时,\(a_n=f(n)\)有最大值,
方法二 根据题意,\(a_{n-1}=-3(n-1)^2+2020(n-1)+1\),
则\(a_n-a_{n-1}=-6n+2023\),
当\(1≤n≤336\)时,\(a_n-a_{n-1}>0\),即\(a_n>a_{n-1}\),
当\(n≥337\)时,\(a_n-a_{n-1}<0\),即\(a_n<a_{n-1}\),
而\(a_{337}>a_{336}\),
故数列\(\{a_n\}\)各项中最大项是第\(337\)项. -
答案 \(\left(-\dfrac{3}{2},+\infty\right)\)
解析 \(\because\)数列\(\{a_n\}\)是递增数列,\(\therefore\)对于任意\(n∈N^*\),\(a_{n+1}>a_n\),
\(\therefore (n+1)^2+2λ(n+1)+1>n^2+2λn+1\),化为: \(\lambda>-\dfrac{2 n+1}{2}\),
\(\because\)数列\(\left\{-\dfrac{2 n+1}{2}\right\}\)单调递减, \(\therefore \lambda>-\dfrac{3}{2}\). -
答案 (1) \(-4\);(2) \(150\)是该数列的第\(16\)项.
解析 (1)根据题意,数列\(\{a_n\}\),\(a_n=n^2-pn+q\),且\(a_1=0\),\(a_2=-4\).
则有\(\left\{\begin{array}{l} 1-p+q=0 \\ 4-2 p+q=-4 \end{array}\right.\),解可得\(\left\{\begin{array}{l} p=7 \\ q=6 \end{array}\right.\),
则\(a_n=n^2-7n+6\),
故\(a_5=25-35+6=-4\),
(2)由(1)的结论,\(a_n=n^2-7n+6\),
若\(a_n=n^2-7n+6=150\),解可得:\(n=16\)或\(-9\)(舍),
故\(n=16\),
\(150\)是该数列的第\(16\)项. -
答案 (1) \(a_n=\dfrac{3 n}{2 n+1}\);(2)略;(3)略.
解析 (1)解:由题意,可知 \(a_2=\dfrac{2 a}{2 b+1}=\dfrac{6}{5}\), \(a_3=\dfrac{3 a}{3 b+1}=\dfrac{9}{7}\),
整理联立方程组,得 \(\left\{\begin{array}{l} 5 a-6 b=3 \\ 7 a-9 b=3 \end{array}\right.\),解得 \(\left\{\begin{array}{l} a=3 \\ b=2 \end{array}\right.\),
\(\therefore a_n=\dfrac{3 n}{2 n+1}\).
(2)证明:由(1),知 \(a_{n+1}=\dfrac{3(n+1)}{2(n+1)+1}=\dfrac{3(n+1)}{2 n+3}\),
则 \(a_{n+1}-a_n=\dfrac{3(n+1)}{2 n+3}-\dfrac{3 n}{2 n+1}=\dfrac{3(n+1)(2 n+1)-3 n(2 n+3)}{(2 n+1)(2 n+3)}\)\(=\dfrac{3}{(2 n+1)(2 n+3)}>0\),
\(\therefore\)数列\(\{a_n\}\)是递增数列.
(3)证明:由(2),可知
当\(n=1\)时,数列\(\{a_n\}\)取得最小值\(a_1=1\),
当\(n→+∞\)时, \(a_n=\dfrac{3 n}{2 n+1}=\dfrac{3}{2+\dfrac{1}{n}} \rightarrow \dfrac{3}{2}\),
\(\therefore 1 \leq a_n<\dfrac{3}{2}\),故得证.
【B组---提高题】
1.对于项数都为\(m\)的数列\(\{a_n\}\)和\(\{b_n\}\),记\(b_k\)为\(a_1,a_2,…,a_k\)\((k=1,2,…,m)\)中的最小值,给出下列命题:
①若数列\(\{b_n\}\)的前\(5\)项依次为\(5,5,3,3,1\),则\(a_4=3\);
②若数列\(\{b_n\}\)是递减数列,则数列\(\{a_n\}\)也是递减数列;
③数列\(\{b_n\}\)可能是先递减后递增的数列;
④若数列\(\{a_n\}\)是递增数列,则数列\(\{b_n\}\)是常数列.
其中,是真命题的为( )
A.①④ \(\qquad \qquad \qquad \qquad\) B.①③ \(\qquad \qquad \qquad \qquad\) C.②③ \(\qquad \qquad \qquad \qquad\) D.②④
2.数列\(\{a_n\}\)的通项公式为\(a_n=\left(\dfrac{4}{5}\right)^{2 n-4}-\left(\dfrac{4}{5}\right)^{n-2}\),则数列\(\{a_n\}\) ( )
A.有最大项,无最小项 \(\qquad \qquad \qquad \qquad\) B.有最小项,无最大项
C.既有最大项又有最小项 \(\qquad \qquad \qquad \qquad\) D.既无最大项又无最小项
3.已知数列\(\{a_n\}\)满足\(a_n=\dfrac{1}{n+1}+\dfrac{1}{n+2}+\dfrac{1}{n+3}+\cdots+\dfrac{1}{2 n}\).
(1)数列\(\{a_n\}\)是递增数列还是递减数列?为什么?
(2)证明:\(a_n \geq \dfrac{1}{2}\)对一切正整数恒成立.
参考答案
-
答案 \(D\)
解析 ①由数列\(\{b_n\}\)的前\(5\)项依次为\(5,5,3,3,1\),
可知\(a_1=5\),\(a_2≥5\),\(a_3=3\),\(a_4≥3\),\(\therefore\)①错误;
②若数列\(\{b_n\}\)是递减数列,则数列\(\{a_n\}\)也是递减数列是正确的;
若数列\(\{a_n\}\)是递增数列或常数列时,则\(\{b_n\}\)是常数列,
若数列\(\{a_n\}\)是递减数列时,则\(\{b_n\}\)是递减的,
\(\therefore\)③是错误的;④是正确的.
故选:\(D\). -
答案 \(C\)
解析 由已知,设 \(t=\left(\dfrac{4}{5}\right)^{n-2}\),
则 \(a_n=t^2-t=\left(t-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\),\((0<t \leq \dfrac{5}{4}\)且随着\(n\)的增大,\(t\)的值一直在减小\()\),
画出其图象如下:

图象开口向上,且对称轴为 \(t=\dfrac{1}{2}\),据图可知,
当\(n=1\),即\(t=\dfrac{5}{4}\)时,\(a_n\)取得最大值\(a_1\),又当\(n=5\)时 \(t=\left(\dfrac{4}{5}\right)^3>\dfrac{1}{2}\),
当\(n=6\)时 \(t=\left(\dfrac{4}{5}\right)^4<\dfrac{1}{2}\),且\(n=5\)时,\(t\)的值更接近\(\dfrac{1}{2}\),
所以当\(n=5\)时,\(a_n\)的值最小.
故选:\(C\). -
答案 (1)略;(2)略.
解析 (1) \(\because a_n=\dfrac{1}{n+1}+\dfrac{1}{n+2}+\dfrac{1}{n+3}+\cdots+\dfrac{1}{2 n}\),
\(\therefore a_{n+1}=\dfrac{1}{(n+1)+1}+\dfrac{1}{(n+1)+2}+\dfrac{1}{(n+1)+3}+\cdots+\dfrac{1}{2(n+1)}\)
\(=\dfrac{1}{n+2}+\dfrac{1}{n+3}+\dfrac{1}{n+4}+\cdots+\dfrac{1}{2 n}+\dfrac{1}{2 n+1}+\dfrac{1}{2 n+2}\),
\(\therefore a_{n+1}-a_n=\dfrac{1}{2 n+1}+\dfrac{1}{2 n+2}-\dfrac{1}{n+1}=\dfrac{1}{2 n+1}-\dfrac{1}{2(n+1)}\),
又\(n∈N^*\),\(\therefore 2n+1<2(n+1)\),\(\therefore a_{n+1}-a_n>0\),
\(\therefore\)数列\(\{a_n\}\)是递增数列.
(2)由(1)知数列\(\{a_n\}\)为递增数列,
所以数列\(\{a_n\}\)的最小项是 \(a_1=\dfrac{1}{2}\),
所以即 \(a_n \geq \dfrac{1}{2}\)对一切正整数恒成立.
【C组---拓展题】
1.数列\(\{a_n\}\)为从\(a_0\)开始的非负整数有限数列,\(a_i\)表示在这个数列中\(i\)出现的次数.那么数列的项数不可能是( )
A.\(4\) \(\qquad \qquad \qquad \qquad\) B.\(5\) \(\qquad \qquad \qquad \qquad\) C.\(6\) \(\qquad \qquad \qquad \qquad\) D.\(7\)
2.(多选)对于数列\(\{a_n\}\),定义: \(b_n=a_n-\dfrac{1}{a_n}\left(n \in N^*\right)\),称数列\(\{b_n\}\)是\(\{a_n\}\)的“倒差数列”.下列叙述正确的有( )
A.若数列\(\{a_n\}\)单调递增,则数列\(\{b_n\}\)单调递增
B.若数列\(\{b_n\}\)是常数列,数列\(\{a_n\}\)不是常数列,则数列\(\{a_n\}\)是周期数列
C.若 \(a_n=1-\left(-\dfrac{1}{2}\right)^n\),则数列\(\{b_n\}\)没有最小值
D.若 \(a_n=1-\left(-\dfrac{1}{2}\right)^n\),则数列\(\{b_n\}\)有最大值
参考答案
-
答案 \(C\)
解析 \(\because a_i\)表示在这个数列中\(i\)出现的次数.
\(\therefore a_0≠0\),且\(a_0≠n\),且\(a_0≠n+1\),
若\(a_1=1\),则当\(i≠1\)时,\(a_i≠1\),\(a_n=0\),
用排除法解答此题;
当\(a_0=2\),\(a_1=0\),\(a_2=2\),\(a_3=0\)时,满足条件,此时数列有\(4\)项,故排除\(A\)答案;
当\(a_0=2\),\(a_1=1\),\(a_2=2\),\(a_3=0\),\(a_4=0\)时,满足条件,此时数列有\(5\)项,故排除\(B\)答案;
当\(a_0=3\),\(a_1=2\),\(a_2=1\),\(a_3=1\),\(a_4 =0\),\(a_5=0\),\(a_6=0\)时,满足条件,此时数列有\(7\)项,故排除\(D\)答案;
故选:\(C\). -
答案 \(BD\)
解析 对于\(A\):函数 \(f(x)=x-\dfrac{1}{x}\)在\((-∞,0)\)和\((0,+∞)\)上单调递增,但在整个定义域上不是单调递增,
可知数列\(\{a_n\}\)单调递增,则数列\(\{b_n\}\)不是单调递增,
例如: \(a_n=n-\dfrac{5}{2}\),则 \(b_2=-\dfrac{1}{2}+2=\dfrac{3}{2}\), \(b_3=\dfrac{1}{2}-2=-\dfrac{3}{2}\),故\(A\)错误;
对于\(B\):数列\(\{b_n\}\)是常数列,可设\(b_n=a_n-\dfrac{1}{a_n}=t\),则 \(a_{n+1}-\dfrac{1}{a_{n+1}}=t\),
\(\therefore a_{n+1}-\dfrac{1}{a_{n+1}}-a_n-\dfrac{1}{a_n}=\left(a_{n+1}-a_n\right)\left(1+\dfrac{1}{a_n a_{n+1}}\right)=0\),
\(\because\) 数列\(\{a_n\}\)不是常数列,
\(\therefore a_{n+1}-a_n≠0\),
\(\therefore 1+\dfrac{1}{a_n a_{n+1}}=0\),整理可得 \(a_{n+1}=-\dfrac{1}{a_n}\),
\(\therefore a_{n+2}=-\dfrac{1}{a_{n+1}}=a_n\),
\(\therefore\) 数列\(\{a_n\}\)是以\(2\)为周期的周期数列,故\(B\)正确;
对于\(CD\),若 \(a_n=1-\left(-\dfrac{1}{2}\right)^n\),则\(b_n=1-\left(-\dfrac{1}{2}\right)^n-\dfrac{1}{1-\left(-\dfrac{1}{2}\right)^n}\),
①当\(n\)为偶数时, \(a_n=1-\dfrac{1}{2^n} \in(0,1)\)且\(\{a_n\}\)单调递增,
\(\therefore \dfrac{1}{a_n}>1>a_n\),
\(\therefore b_n<0\),且数列\(\{b_n\}\)单调递增,
此时\(\left(b_n\right)_{\min }=b_2=1-\dfrac{1}{4}-\dfrac{1}{1-\dfrac{1}{4}}=\dfrac{3}{4}-\dfrac{4}{3}=-\dfrac{7}{12}\),
①当\(n\)为奇数时, \(a_n=1+\dfrac{1}{2^n}>1\)且\(\{a_n\}\)单调递减,
\(\therefore a_n>1>\dfrac{1}{a_n}\) ,
\(\therefore b_n>0\),且数列\(\{b_n\}\)单调递减,
此时\(\left(b_n\right)_{\max }=b_1=1+\dfrac{1}{2}-\dfrac{1}{1+\dfrac{1}{2}}=\dfrac{3}{2}-\dfrac{2}{3}=\dfrac{5}{6}\),
综上所述列\(\{b_n\}\)既有最大值\(\dfrac{5}{6}\),也有最小值\(-\dfrac{7}{12}\),
故\(C\)错误,\(D\)正确.
故选:\(BD\).