树链剖分
定理
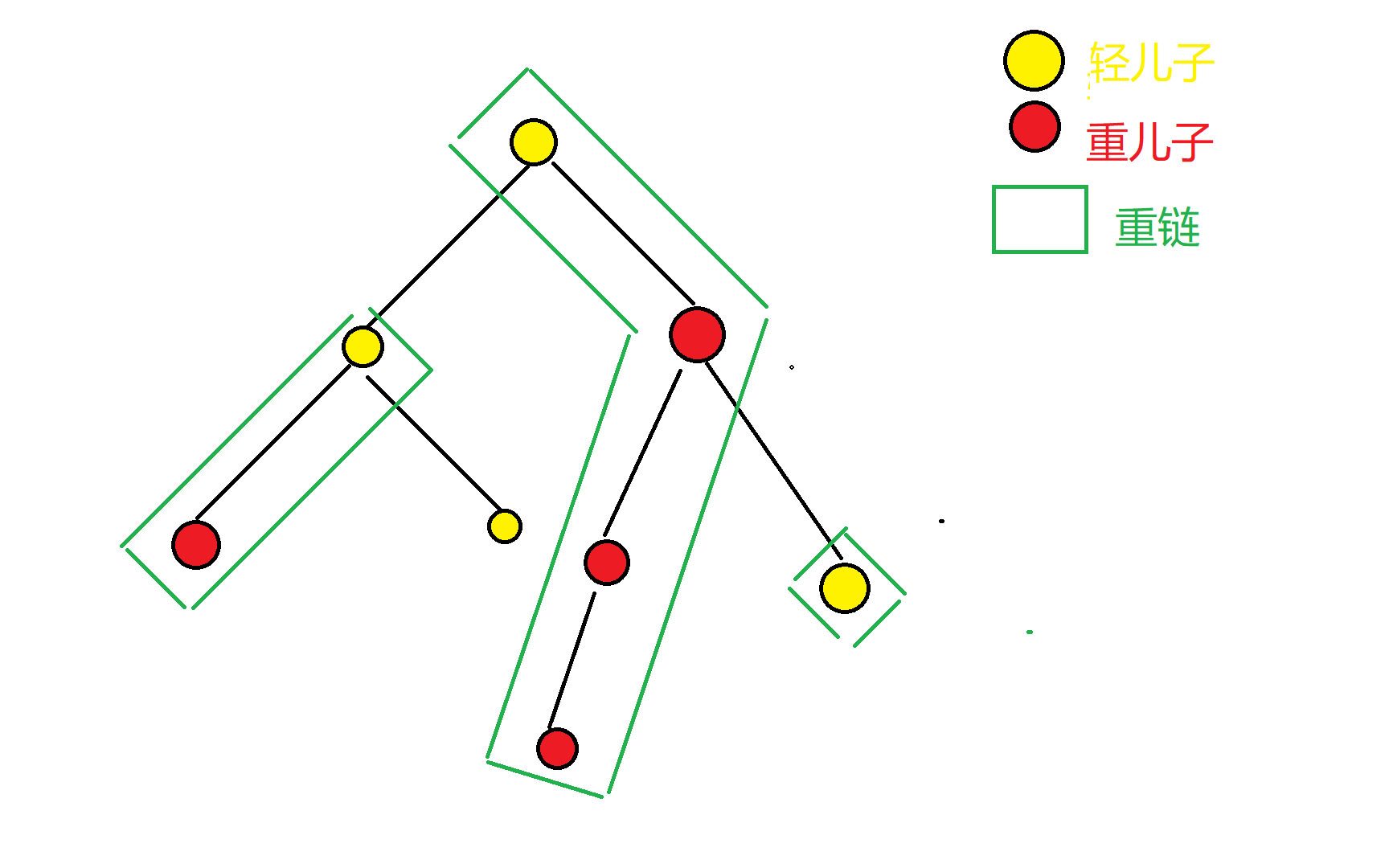
- 重儿子:一个节点所有儿子中,子树大小最大的儿子即为重儿子,如有多个,任取一个即可。
- 轻儿子:除了重儿子外的所有儿子。
- 重边:父节点 \(\to\) 重儿子的边。
- 重链:由重边构成的极大链。
如以下图。
过程
\(dfs\) 序:优先遍历重儿子,这样就可以保证重链上所有点的编号连续。
如下图,蓝色数字即为求完 \(dfs\) 序后所有点的编号。
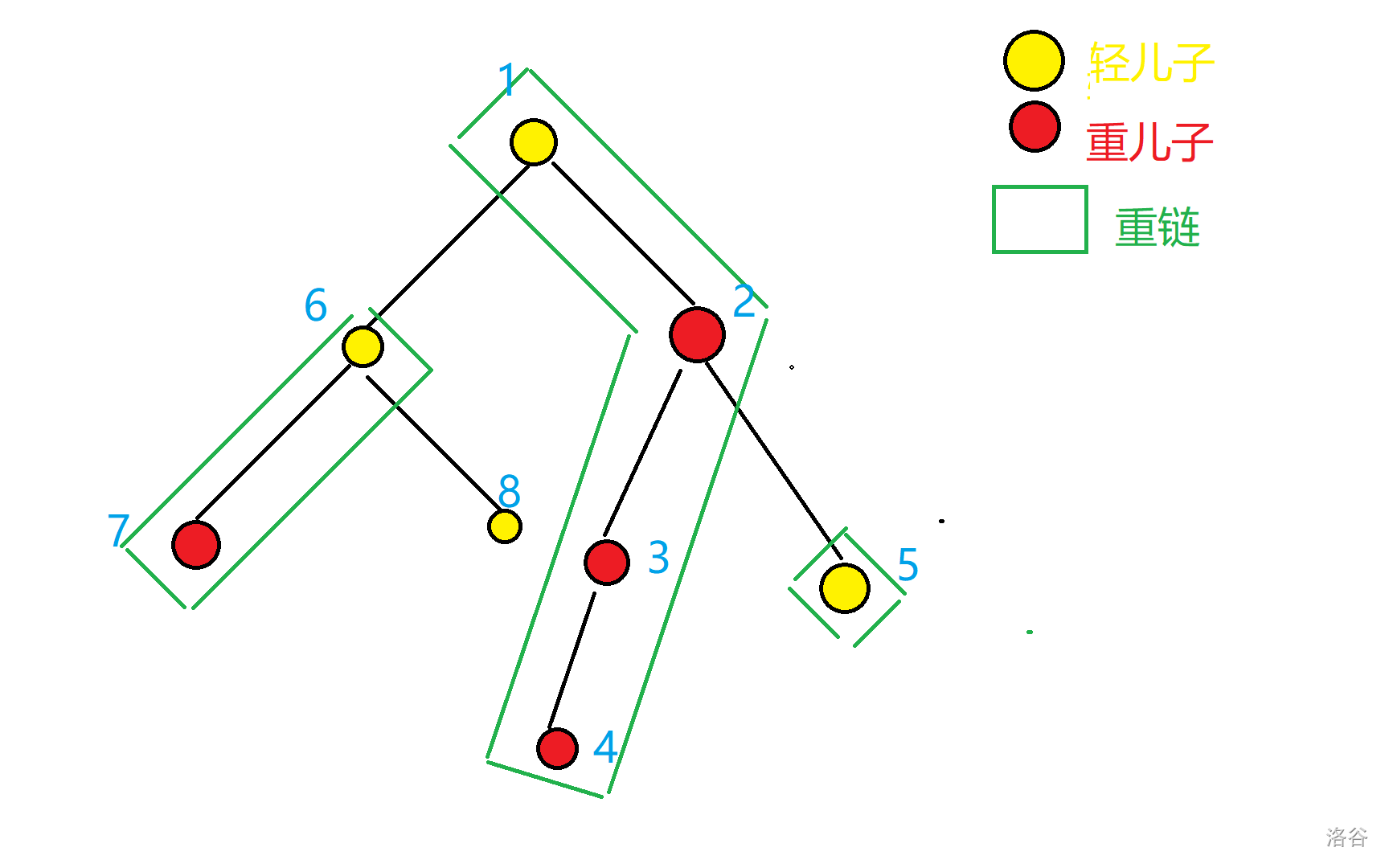
求完 \(dfs\) 序即将树转化成序列。
定理:树中任意一条路径均可拆分成小于等于 \(\log n\) 条重链,即可拆分成小于等于 \(\log n\) 连续区间。
将一条路径拆分成若干条条重链
这个过程类似于倍增求 \(lca\)。
假设求 \(x, y\) 的若干条重链。
如果 \(f_x > f_y\) 则先将 \(x\) 跳到该节点所在重链的顶部再走到他的父节点上。
如果 \(f_y > f_x\) 则先将 \(y\) 跳到该节点所在重链的顶部在走到他的父节点上。
其中 \(f\) 表示该节点的深度,即该节点在树的第几层。
最后一定会走到同一条重链上。
以上操作可以用线段树/分块/Splay 来维护。
例题
\(\mathcal Preface\)
\(\mathcal Solution\)
- 操作 \(\mathit{1 \sim 2}\):即用前述的树链剖分的思想。
- 操作 \(\mathit{3 \sim 4}\):即把 \(dfs\) 序的一段连续区间求和或修改。
维护就与此题类似。
标签:浅谈,剖分,dfs,儿子,树链,重链,节点 From: https://www.cnblogs.com/hcywoi/p/16948187.html