矩阵乘法
首先给出矩阵乘法的代数意义:
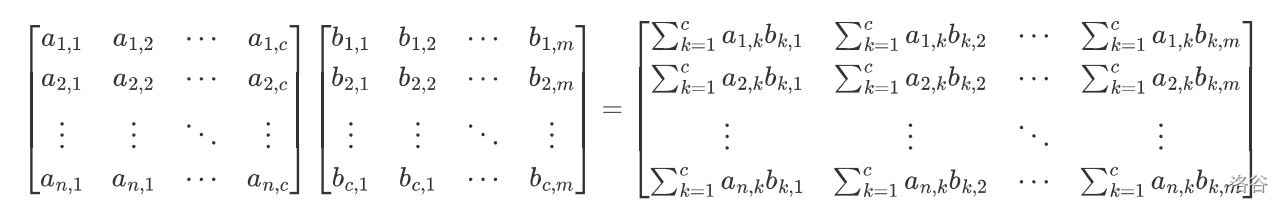
结合一个具体的例子来理解:
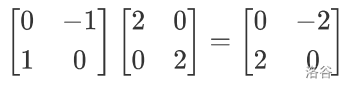
设答案矩阵为 \(ans\) 。根据公式:
\(ans_{1,1}\) 是由 \(a\) 矩阵的第一行与 \(b\) 矩阵的第一列逐位相乘并求和得到的。
\(ans_{1,2}\) 是由 \(a\) 矩阵的第一行与 \(b\) 矩阵的第二列逐位相乘并求和得到的。
\(ans_{2,1}\) 是由 \(a\) 矩阵的第二行与 \(b\) 矩阵的第一列逐位相乘并求和得到的。
\(ans_{2,2}\) 是由 \(a\) 矩阵的第二行与 \(b\) 矩阵的第二列逐位相乘并求和得到的。
由此,可以简单理解,矩阵乘法得出的结果,\(ans_{i,j}\) 是由 \(a\) 矩阵的第 \(i\) 行与 \(b\) 矩阵的第 \(j\) 列逐位相乘并求和得到的。同时,也可以得知,一般情况下,要做矩阵乘法,\(a\) 矩阵的列数应该和 \(b\) 矩阵的行数相同。
根据这一结论,我们就可以写出矩阵乘法的代码:
struct node{
ll p[105][105];
};
node X(node a,node b){
node t;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
t.p[i][j]=0;
for(int k=1;k<=n;k++){
t.p[i][j]+=a.p[i][k]*b.p[k][j];
t.p[i][j]%=mod;
}
}
}
return t;
}
矩阵快速幂
了解了矩阵乘法,就可以做矩阵快速幂了。
对于矩阵 \(A\) ,\(A^k\) 就表示 \(k\) 个 \(A\) 矩阵相乘。
先回顾一下快速幂。快速幂的做法是将指数每次折半。这样可以把效率提到 \(log n\)。
例如求 \(a^{2n+1}\) 时,就可以转成 \(a^{n}\times a^{n}\times a\)。求\(a^{2n}\) 时,就可以转成 \(a^{n}\times a^{n}\)。
根据这个思路,就有了快速幂板子:
P1226 【模板】快速幂||取余运算
ll fpow(ll a,ll p){
ll ans=1;
while(p){
if(p&1) ans=ans*a%mod;
a=a*a%mod;
p>>=1;
}
return ans;
}
至于光速幂,咱也不懂qwq
光速幂
回归正题,那么矩阵快速幂也同理。只要把普通快速幂中的乘法换成矩阵乘法就可以了。写成代码就是这样:
node fpow(node a,ll k){
node ans=a,b=a;
while(k){
if(k&1) ans=X(b,ans);
b=X(b,b);
k>>=1;
}
return ans;
}
需要注意的是,\(k\) 的值在传入时,需要 \(-1\) ,因为矩阵的一次幂就是本身,相当于已经乘过一次了。
结合矩阵乘法,我们就可以得到矩阵快速幂的完整板子:
P3390 【模板】矩阵快速幂
#include<bits/stdc++.h>
#define ll long long
#define mod 1000000007
using namespace std;
ll n,k;
struct node{
ll p[105][105];
}a;
node X(node a,node b){
node t;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
t.p[i][j]=0;
for(int k=1;k<=n;k++){
t.p[i][j]+=a.p[i][k]*b.p[k][j];
t.p[i][j]%=mod;
}
}
}
return t;
}
node fpow(node a,ll k){
node ans=a,b=a;
while(k){
if(k&1) ans=X(b,ans);
b=X(b,b);
k>>=1;
}
return ans;
}
int main(){
scanf("%lld%lld",&n,&k);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) scanf("%lld",&a.p[i][j]);
}
a=fpow(a,k-1);
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++) printf("%lld ",a.p[i][j]);
printf("\n");
}
return 0;
}
一道用到矩阵快速幂的例题:
P1962 斐波那契数列
十分巧妙地用了矩阵快速幂加速递推过程。具体可以看题解,这里不多赘述。
#include<bits/stdc++.h>
#define ll long long
#define mod 1000000007
using namespace std;
ll n;
struct node{
ll p[15][15];
}a,ans;
node X(node a,node b){
node t;
for(int i=1;i<=2;i++){
for(int j=1;j<=2;j++){
t.p[i][j]=0;
for(int k=1;k<=2;k++){
t.p[i][j]+=a.p[i][k]*b.p[k][j];
t.p[i][j]%=mod;
}
}
}
return t;
}
void fpow(ll k){
while(k){
if(k&1) ans=X(a,ans);
a=X(a,a);
k>>=1;
}
}
int main(){
scanf("%lld",&n);
if(n<=2){
printf("1");
return 0;
}
a.p[1][1]=a.p[1][2]=a.p[2][1]=1;
ans.p[1][1]=ans.p[1][2]=1;
fpow(n-1);
printf("%lld",ans.p[1][1]);
return 0;
}
高斯消元
高斯消元法用于解线性方程组。
那么什么是线性方程组呢?
线性方程组就是有多个未知数,并且每个未知数的次数均为一次,这样多个未知数组成的方程组为线性方程组。或者我们也可以叫它多元一次方程组。
比如以下这个方程组:
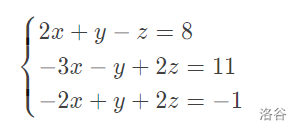
数学老师教我们,多元一次方程组可以用加减消元法和代入消元法求解。
高斯消元法其实就是这样求解的。先进行加减消元,我们可以先求得一个未知数的值,然后可以逐层往回代(代入消元法),依次可以得到第 \(2\) 个、第 \(3\) 个未知数的值,最终解出方程组中各个未知数的值,结束算法。
那如何具体实现?
首先,提出各项系数并转化成一个矩阵。比如上面的方程就可以转化为:
\(\begin{bmatrix} 2&1&-1&|&8\\-3&-1&2&|&11\\-2&1&2&|&-1\end{bmatrix}\)
然后考虑我们做数学时一般解方程思路。我们往往是将系数绝对值最大的方程转移到被减的这一行,方便计算,也可以减小误差。
所以接下来要做的是将 \(x\) 项系数绝对值最大的放到第一行。变化之后矩阵变成这样:
\(\begin{bmatrix} -3&-1&2&|&11\\2&1&-1&|&8\\-2&1&2&|&-1\end{bmatrix}\)
这一步代码实现非常简单,若当前解的是第 \(i\) 个未知数,只要找出 $\max ${ \(fabs(A_{j,i})\) } 即可。其中 \(fabs\) 就是对浮点数取绝对值。设 \(j=r\) 时取到最大,就将第 \(r\) 行与第 \(i\) 行逐项互换就可以了。代码:
r=i;
for(int j=i+1;j<n;j++){
if(fabs(a[j][i])>fabs(a[r][i])) r=j;
}
if(r!=i) for(int j=0;j<=n;j++) swap(a[i][j],a[r][j]);
之后,对于下面的每一行(记为 \(L_{k}\)),我们可以求出一个比值 \(f=A_{k,i}/A_{i,i}\) 。我们要将 \(L_k\) 的每一项 \(A_{k,j}\) 都减去 $ A_{i,j}\times f $,达到加减消元的目的(可以手算理解)。比如上面这个经处理的矩阵,经过第一次加减消元后会变成:
\(\begin{bmatrix} -3&-1&2&|&11\\0&\frac{1}{3}&\frac{1}{3}&|&\frac{2}{3}\\0&\frac{5}{3}&\frac{2}{3}&|&\frac{13}{3}\end{bmatrix}\)
相当于:
\(L_2\) 变成了 \(L_2-L_1\times(-\frac{2}{3})\)
\(L_3\) 变成了 \(L_3-L_1\times\frac{2}{3}\)
重复上面的步骤:
交换第 \(2,3\) 行(因为\(\frac{5}{3}>\frac{1}{3}\)),得到:
\(\begin{bmatrix} -3&-1&2&|&11\\0&\frac{5}{3}&\frac{2}{3}&|&\frac{13}{3}\\0&\frac{1}{3}&\frac{1}{3}&|&\frac{2}{3}\end{bmatrix}\)
第二次加减消元,得到:
\(\begin{bmatrix} -3&-1&2&|&11\\0&\frac{5}{3}&\frac{2}{3}&|&\frac{13}{3}\\0&0&\frac{1}{5}&|&-\frac{1}{5}\end{bmatrix}\)
相当于:
\(L_3\) 变成了 \(L_3-L_2\times\frac{1}{5}\)
贴上加减消元这整一部分的代码:
for(int i=0;i<n;i++){
r=i;
for(int j=i+1;j<n;j++){
if(fabs(a[j][i])>fabs(a[r][i])) r=j;
}
if(r!=i) for(int j=0;j<=n;j++) swap(a[i][j],a[r][j]);
for(int k=i+1;k<n;k++){
double f=a[k][i]/a[i][i];
for(int j=i;j<=n;j++) a[k][j]-=f*a[i][j];
}
}
下一步就是进行回带了。
先手算:当前矩阵的第三行重新转回数学式子就是 \(\frac{1}{5}z=-\frac{1}{5}\),所以易得 \(z=A_{2,3}/A_{2,2}=-1\)。然后把 \(z=-1\) 带入第二行,可以得到 \(\frac{5}{3}y+\frac{2}{3}\times(-1)=\frac{13}{3}\) 这时我们只要把 \(\frac{13}{3}\) 减掉 \(\frac{2}{3}\times(-1)\),也就是移项,再除以 \(\frac{5}{3}\) 就能得到 \(y\)。以此类推。
所以我们就得到方法:先将等式右边减掉所有等式左边的已知项,再除以未知项系数就好了。具体可以根据代码理解:
for(int i=n-1;i>=0;i--){
for(int j=i+1;j<=n;j++) a[i][n]-=a[j][n]*a[i][j];
a[i][n]/=a[i][i];
}
最后,我们需要判断无解或不唯一解的情况。
仍然从数学上理解,我们知道,对于一次方程,当方程的所有未知数系数都为 \(0\),但常数项不为 \(0\) 时,方程无解。例如 \(0x+0y+0z=114\) ,显然无解。
同样,对于一次方程,当方程的所有未知数系数都为 \(0\),而常数项也为 \(0\) 时,方程有无数解。例如 \(0x+0y+0z=0\) 。
所以,转化到矩阵中,当存在一行 \(L_x\) ,其 \(A_{x,0}\) 到 \(A_{x,n-1}\) 都为 \(0\) 但 \(A_{x,n} \ne 0\) 时,方程组无解。同样,当存在一行 \(L_x\) ,其 \(A_{x,0}\) 到 \(A_{x,n-1}\) 都为 \(0\) 且 \(A_{x,n} = 0\) 时,方程组有无数解。(洛谷 P3389 只问是否有唯一解,所以两种情况可以合并讨论)。
下面是完整代码:
P3389 【模板】高斯消元法
#include<bits/stdc++.h>
using namespace std;
int n,r,fl;
double a[105][105];
void gauss(){
for(int i=0;i<n;i++){
r=i;
for(int j=i+1;j<n;j++){
if(fabs(a[j][i])>fabs(a[r][i])) r=j;
}
if(r!=i) for(int j=0;j<=n;j++) swap(a[i][j],a[r][j]);
for(int k=i+1;k<n;k++){
double f=a[k][i]/a[i][i];
for(int j=i;j<=n;j++) a[k][j]-=f*a[i][j];
}
}
for(int i=0;i<n;i++){
int kk=0;
for(int j=0;j<n;j++) if(a[i][j]!=0) kk=1;
if(!kk){
fl=1;
return ;
}
}
for(int i=n-1;i>=0;i--){
for(int j=i+1;j<=n;j++) a[i][n]-=a[j][n]*a[i][j];
a[i][n]/=a[i][i];
}
}
int main() {
scanf("%d",&n);
for(int i=0;i<n;i++){
for(int j=0;j<=n;j++) scanf("%lf",&a[i][j]);
}
gauss();
if(fl){
printf("No Solution");
return 0;
}
for(int i=0;i<n;i++) printf("%.2lf\n",a[i][n]);
return 0;
}
线性基
对于一组数 \(A_1\) ~ \(A_n\) ,它们的线性基为 \(P_1\) ~ \(P_n\)。其中 \(P_i\) 表示二进制下出现 \(1\) 的最高位在第 \(i\) 位的数。
所以,线性基可以方便地求最大异或和。
先看线性基的构造方法。
比如说给定这样一组数构造线性基:\(5,11,17,24\)。
首先将每一个数转化为二进制:
\(5->101\)
\(11->1011\)
\(17->10001\)
\(24->11000\)
然后我们从依次最高位开始找。
如果最高位的 \(1\) 在第 \(i\) 位,并且当前的 \(P_i=0\) 我们就把 \(P_i\) 赋值为这个数。例如处理 \(5\),就把 \(P_2\) 赋值为 \(5\)。
如果当前的 \(P_i \ne 0\) ,那就让当前的数 \(\oplus=P_i\) ,也就是把所有与 \(P_i\) 重复的 \(1\) 抹掉并继续往后搜。
例如处理 \(24\) ,此时 \(P_4\) 已经是 \(17\) 了,就把 \(24 \oplus=17\) 得到 \(9(1001)\)。
又发现此时 \(P_3\) 已经是 \(11\) 了,就把 \(9 \oplus=11\) 得到 \(2(10)\) 。
此时 \(P_1=0\),就把 \(P_1\) 赋值为 \(2\)。
按照手算的过程,我们可以写出代码:
void make(ll a){
for(int i=52;i>=0;i--){
if(a>>(ll)i){
if(!p[i]){
p[i]=a;
break;
}
else a^=p[i];
}
}
return ;
}
再来看如何寻找答案:
简单手算一下,可以发现,求最大异或和是满足贪心的,且对顺序没有要求。
这里可以简单证明:因为异或是不进位运算,所以高位不受低位影响。举几个例子:
- \(10001 \oplus 1000 = 11001\) ,显然更优。
- \(10111 \oplus 1111 = 11000\) ,虽然低位变小,但高位更大了,所以结果还是更优。
- \(11000 \oplus 1111 = 10111\) ,虽然低位变大,但高位更小了,所以结果更劣。
所以,得出:只要将 \(ans\) 对所有 \(P_i\) 从高位到低位异或一遍,就可以得到最优答案。
下面是完整代码:
P3812 【模板】线性基
#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,a[60],p[60],ans;
void make(ll a){
for(int i=52;i>=0;i--){
if(a>>(ll)i){
if(!p[i]){
p[i]=a;
break;
}
else a^=p[i];
}
}
return ;
}
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lld",&a[i]);
make(a[i]);
}
for(int i=52;i>=0;i--) ans=max(ans,ans^p[i]);
printf("%lld",ans);
return 0;
}