我们称一个长度为 2n 的数列是有趣的,当且仅当该数列满足以下三个条件:
- 它是从 1 到 2n 共 2n 个整数的一个排列 {ai};
- 所有的奇数项满足 a1<a3<⋯<a2n−1 ,所有的偶数项满足 a2<a4<⋯<a2n;
- 任意相邻的两项 a2i−1 与 a2i (1≤i≤n) 满足奇数项小于偶数项,即:a2i−1<a2i。
任务是:对于给定的 n,请求出有多少个不同的长度为 2n 的有趣的数列。
因为最后的答案可能很大,所以只要求输出答案 modP 的值。
输入格式
只包含用空格隔开的两个整数 n 和 P。
输出格式
仅含一个整数,表示不同的长度为 2n 的有趣的数列个数 modP 的值。
数据范围
1≤n≤106,2≤P≤109
输入样例:
3 10
输出样例:
5
样例解释
对应的 5 个有趣的数列分别为 {1,2,3,4,5,6},{1,2,3,5,4,6},{1,3,2,4,5,6},{1,3,2,5,4,6},{1,4,2,5,3,6}。
| 难度:中等 |
|---|
| 时/空限制:1s / 64MB |
| 总通过数:1138 |
| 总尝试数:1814 |
| 来源:《信息学奥赛一本通》,HNOI2009 |
| 算法标签 |
核心思路:看到组合数学无非就那么些方法,隔板法,还有就是卡特兰数。但是我们很难发现哪些是需要用到卡特兰数的。所以我们必须对它的性质进一步推导
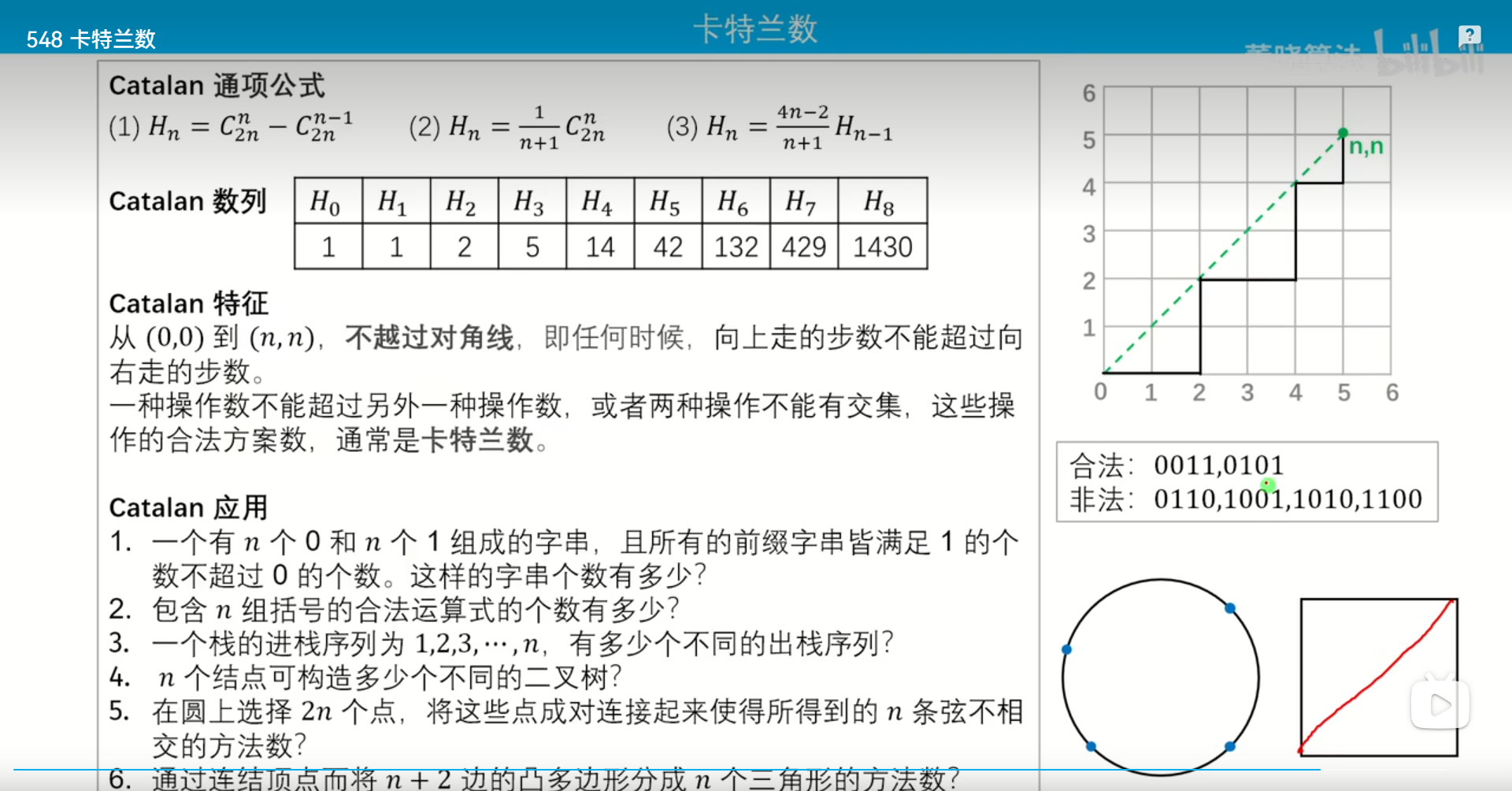
卡特兰数的定义:以走网格为例,从格点(0,0)走到(n,n),只能向右和向上走,并且不可以越过y=x这条直线的条数,这就是卡特兰数记为\(H_n\).我们把0记为向上走,1记为向右走,所以也就是前缀0的次数不可以大于1的次数。
也就是这个题目:[01序列](找不到页面 - AcWing)
通项公式:(1)\(H_n=C_{2n}^{n}-C_{2n}^{n-1}\) (2)\(H_n=C_{2n}^{n}/(n+1)\) (3)\(H_n=\frac{4n-2}{n+1}H_{n-2}\).
通俗点讲就是一种操作数不可以超过另外一种,或者两种操作数不可以有交集,这些操作就是合法的方案数,也就是卡特兰数
接下来知道这个背景后我们该怎么做题呢,我们随意构造一项会发现\(H_3=5\),注意我们是有\(H_0\)的,所以这是我们的第四项。然后我们就初步猜想这是卡特兰数。进一步通过性质验证。
我们先把前\(1\sim5个数\)放入我们要构造的数列。如果前缀奇数项个数大于偶数项个数就无法构造。
比如:1 3 2 4 _ 5
此时奇数项cnt(1,2,5)=3>偶数项cnt(2,4).就会出现中间那个数无法构造了。注意我们这里的奇数项和偶数项是指每一项的下标,而不是下标对应的数。其实我们也可以把这个奇数和偶数出现的次序看成01序列的操作。
这个是题目背景:董晓算法
#include <bits/stdc++.h>
#define LL long long
using namespace std;
const int N = 2e6 + 10;
int n, mod;
int primes[N], cnt;
bool st[N];
int get(int n, int p)//求n中p的质因数的个数
{
int s = 0;
while (n)
{
s += n / p;
n /= p;
}
return s;
}
void Inite(int n)
{
for (int i = 2;i <= n;i++)
{
if (!st[i])
primes[cnt++] = i;
for (int j = 0;primes[j] * i <= n;j++)
{
st[primes[j] * i] = 1;
if (i % primes[j] == 0)
break;
}
}
}
int qmi(int a, int b)
{
int res = 1;
while (b)
{
if (b & 1)
res = (LL)res * a % mod;
b >>= 1;
a = (LL)a * a % mod;
}
return res;
}
int C(int a,int b)
{
int res = 1;
for (int i = 0;i < cnt;i++)
{
int p = primes[i];
int s = get(a, p) - get(a - b, p) - get(b, p);
res=(LL)res*qmi(p,s)%mod;
}
return res;
}
int main()
{
cin >> n >> mod;
Inite(n*2);
cout << (C(2 * n, n) - C(2 * n, n - 1) + mod) % mod;
}