### T1
题目:P1469
思路:
输出所有数异或的结果就好了。
因为异或有如下两个性质:
-
\(x \oplus x = 0\)
-
\(x \oplus 0 = x\)
所以全部数的异或和,等同于两两消去相同的数后的异或和。
按照题目要求,这个就是答案啦。
整体评价:
好简单,有点思维挑战。
代码这么简单,不贴了。
T2
题目:P3918
思路1(正解):
这里需要用到异或的另一个性质:
如果 \(x\) 是偶数,则 \(x \oplus (x+1) = 1\)。
列个竖式就容易理解了:
\[\space \space \space \space \space ABCDE\cdots Z0 \]\[\space \underline{\oplus \space ABCDE\cdots Z1} \]\[\space \space \space \space \space 0\space0\space0\space0\space0\space\cdots \space0\space1 \]然后,分类讨论即可。
若 \(n\equiv0\pmod{4}\),例如 \(1\boxed{23}\boxed{45}\boxed{67}8\),即可转换成:
\(1\boxed{1}\boxed{1}\boxed{1}8\),再将所有 \(1\) 两两抵消,最后只剩 \(8\)。
所以这种情况的结果是 \(n\)。
若 \(n\equiv1\pmod{4}\),例如 \(1\boxed{23}\boxed{45}\),即可转换成:
\(1\boxed{1}\boxed{1}\),再将两个 \(1\) 抵消,最后只剩 \(1\)。
所以这种情况的结果是 \(1\)。
若 \(n\equiv2\pmod{4}\),例如 \(1\boxed{23}\boxed{45}6\),即可转换成:
\(1\boxed{1}\boxed{1}6\),再将两个 \(1\) 抵消,最后只剩 \(1\) 与 \(6\)。
引入一个新性质: \(n\) 为偶数时 \(1 \oplus n = n+1\)。
所以这种情况的结果是 \((n+1)\)。
若 \(n\equiv3\pmod{4}\),例如 \(1\boxed{23}\boxed{45}\boxed{67}\),即可转换成:
\(1\boxed{1}\boxed{1}\boxed{1}\),再将所有 \(1\) 抵消,最后只剩 \(0\)。
所以这种情况的结果是 \(0\)。
思路2(打表):
快速打一个暴力,代码如下。
LL n, ans = 0;
scanf("%lld", &n);
for (LL i = 1; i <= n; i++) ans ^= i;
printf("%lld", ans);
return 0;
可以获得 \(40\) 分的暴力分。
然后,给它加一个嵌套,观察 \(1\) 至 \(20\) 的答案有什么规律。
代码如下。
#include <iostream>
#include <cstdio>
using namespace std;
int main()
{
for (int n = 1; n <= 20; n++)
{
int ans = 0;
for (int i = 1; i <= n; i++) ans ^= i;
printf("n = %d, ans = %d;\n", n, ans);
}
return 0;
}
显示结果如下:
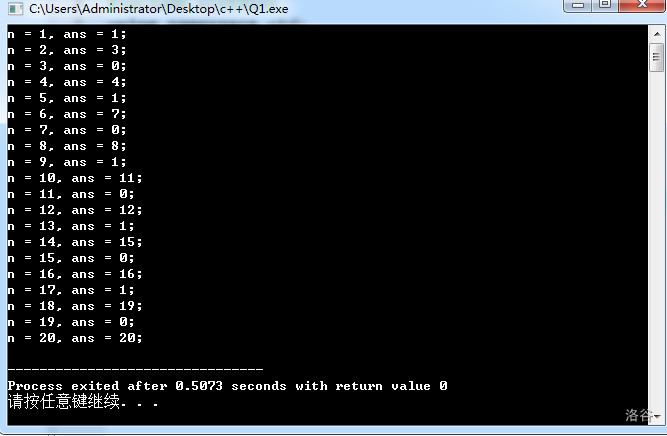
每四个数分一段,非常容易找到规律。
所以,这种策略在考试时是非常可靠的。
整体评价:
比 T1 更难想,但有思路后推起来是很顺的。
代码很简单,同样不贴了。
注意开 long long 哦。
T3
题目:P3951
思路:
题目的意思是:
若 \(n\) 与 \(m\) 互质,求 \(k\) 的最大值使得 \(n \cdot x + m \cdot y = k\) 无解。
列一个表。
举例来说,若 \(m = 7\),\(n = 4\):
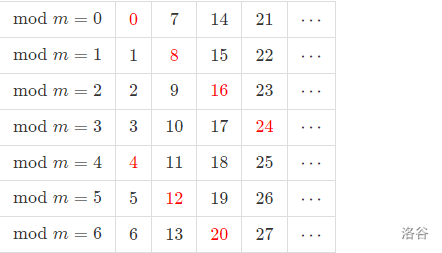
(前台表格炸了,只能在后台截图)
标红的数字都是 \(n\) 的倍数。
你会发现前 \(m\) 个 \(n\) 的倍数恰好占据了每一行。
为什么呢?
两个 \(n\) 的倍数差必为 \(x\cdot n\),在 \(0 \le x \le m-1\) 的前提下:
-
\(n\) 与 \(m\) 互质。
-
\(x\) 与 \(m\) 也互质。
则,这个跨度一定不会是 \(m\) 的倍数。
进一步讲,在范围内,不会有两个 \(n\) 的倍数在同一行。
这些红色的数可以用 \(n \cdot x + 0\) 得到。
在红色数字之后的数(这里指同一行后面的数)也可以凑,因为后面的数可以等同于:红色数字加上 \(m \cdot y\)。
所以,只有红色数字前面(这里指同一行前面的数)的数不能凑成。
最大的红色数字是: \(n\cdot (m-1)\)。
它同一行前一个数是: \(n\cdot (m-1) - m\),化简得 \(n\cdot m - n - m\)。
这个就是答案了,至此本题结束。
拓展:
事实上,你还可以计算不能凑成的数的个数。
式子其实很好列,\(cnt = \left\lfloor\dfrac{n}{m}\right\rfloor + \left\lfloor\dfrac{2n}{m}\right\rfloor + \cdots + \left\lfloor\dfrac{(m-1)n}{m}\right\rfloor\)。
其中,\(n\)、\(2n\cdots(m-1)n\) 是红色的数。
显然,\(n\)、\(2n\cdots(m-1)n\) 都不能整除 \(m\),故此算式直接代表红色数同一行前面的数的个数。
接下来,我们对这个式子化简。
先引入一个简单且容易理解的公式:
若 \(\left\lfloor a\right\rfloor + \left\lfloor b\right\rfloor = k\),且 \(a\) 与 \(b\) 都不是整数,
则 \(a + b = k-1\)。
考虑首尾配对。
\(\begin{aligned}\left\lfloor\dfrac{x\cdot n}{m}\right\rfloor + \left\lfloor\dfrac{(m-x)\cdot n}{m}\right\rfloor & = \dfrac{x\cdot n}{m} + \dfrac{(m-x)\cdot n}{m} - 1\\ & = \dfrac{(x+m-x)\cdot n}{m}-1\\ & = \dfrac{m\cdot n}{m}-1\\ & = n-1\end{aligned}\)
接下来需要分类讨论。
-
若 \(m\) 为奇数,即:有偶数项形如 \(\left\lfloor\dfrac{x\cdot n}{m}\right\rfloor\) 的东西。
首尾配对,共有 \(\dfrac{m-1}{2}\) 组。
因此易得,原式等于:
\(\dfrac{m-1}{2} \times (n-1) = \dfrac{(m-1)(n-1)}{2}\)。
这个 \(\dfrac{(m-1)(n-1)}{2}\) 即答案。
-
若 \(m\) 为偶数,即:有奇数项形如 \(\left\lfloor\dfrac{x\cdot n}{m}\right\rfloor\) 的东西。
此时首尾配对,中项会配不到。
中项是第 \(\dfrac{1+(m-1)}{2} = \dfrac{m}{2}\) 项。
所以,中项的值为 \(\left\lfloor\dfrac{\frac{m}{2} \times n}{m}\right\rfloor = \left\lfloor\dfrac{n}{2}\right\rfloor\)。
由于 \(n\) 与 \(m\) 互质,则 \(n\) 只能是奇数。
所以 \(\left\lfloor\dfrac{n}{2}\right\rfloor = \dfrac{n-1}{2}\)。
除去中项外其他数首尾配对,共有 \(\dfrac{m-2}{2}\) 组。
因此易得,原式等于 \(\dfrac{m-2}{2} \times (n-1)\)。
答案为两者相加,即:
\(\begin{aligned}\dfrac{n-1}{2} + \dfrac{m-2}{2} \times (n-1)&=\dfrac{n-1 + (m-1)(n-1)}{2}\\ & = \dfrac{(m-1)(n-1)}{2}\end{aligned}\)
两种情况答案均为 \(\dfrac{(m-1)(n-1)}{2}\),所以最终答案就是 \(\dfrac{(m-1)(n-1)}{2}\)。
是不是很好玩呢?!
整体评价:
思维难度挺高的。
代码同样不贴了,但是记得开 long long。
首发:2022-04-30 10:20:44