决策树原理
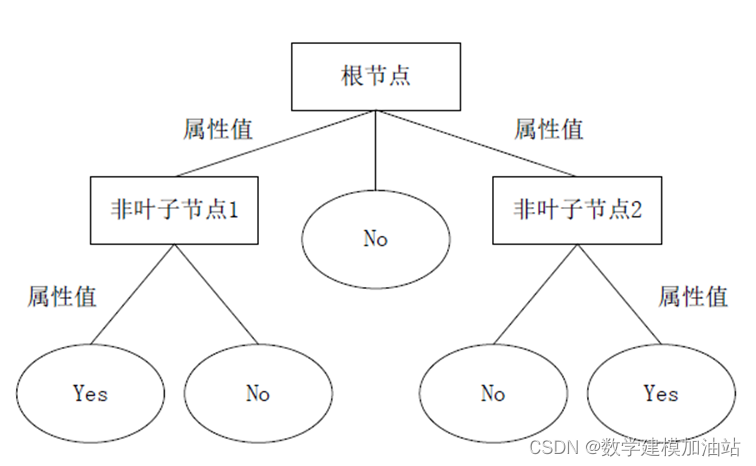
决策树通过把样本实例从根节点排列到某个叶子节点来对其进行分类。树上的每个非叶子节点代表对一个属性取值的测试,其分支就代表测试的每个结果;而树上的每个叶子节点均代表一个分类的类别,树的最高层节点是根节点。
编辑
由上图可知,决策树采用自顶向下的递归方式,从树的根节点开始,在它的内部节点上进行属性值的测试比较。然后按照给定实例的属性值确定对应的分支,最后在决策树的叶子节点得到结论。这个过程在以新的节点为根的子树上重复。
决策树的优点与缺点
优点:
决策树容易理解和实现。
对于决策树,数据的准备往往是比较简单或者是不必要的。其它技术往往要求先把数据归一化,比如去掉多余的或者空白的属性。
能够同时处理数据型和常规型属性。其它的技术往往要求数据属性的单一。
是一个白盒模型。如果给定一个观察的模型,那么根据所产生的决策树很容易推出相应的逻辑表达式。
缺点
对于各类别样本数量不一致的数据,在决策树当中信息增益的结果偏向于那些具有更多数值的特征。
决策树内部节点的判别具有明确性,这种明确性可能会带来误导。
随机森林
随机森林算法基于Bootstrap方法重采样,产生多个训练集。不同的是,随机森林算法在构建决策树的时候,采用了随机选取分裂属性集的方法。
代码实战
1、决策树分类代码
%% I. 清空环境变量
clear all
clc
warning off
%% II. 导入数据 第一列是序号 第二列是良性还是恶性(乳腺癌) 后面是特征属性30个
load data.mat
%%
% 1. 随机产生训练集/测试集
a = randperm(569);
Train = data(a(1:500),:); %产生500个训练集
Test = data(a(501:end),:); %剩下的是测试集 69个
%%
% 2. 训练数据
P_train = Train(:,3:end);
T_train = Train(:,2);
%%
% 3. 测试数据
P_test = Test(:,3:end);
T_test = Test(:,2);
%% III. 创建决策树分类器
ctree = ClassificationTree.fit(P_train,T_train);
%%
% 1. 查看决策树视图
view(ctree);
view(ctree,'mode','graph');
%% IV. 仿真测试
T_sim = predict(ctree,P_test);
%% V. 结果分析
count_B = length(find(T_train == 1));
count_M = length(find(T_train == 2));
rate_B = count_B / 500;
rate_M = count_M / 500;
total_B = length(find(data(:,2) == 1));
total_M = length(find(data(:,2) == 2));
number_B = length(find(T_test == 1));
number_M = length(find(T_test == 2));
number_B_sim = length(find(T_sim == 1 & T_test == 1));
number_M_sim = length(find(T_sim == 2 & T_test == 2));
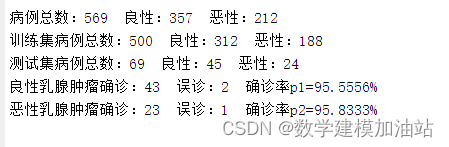
disp(['病例总数:' num2str(569)...
' 良性:' num2str(total_B)...
' 恶性:' num2str(total_M)]);
disp(['训练集病例总数:' num2str(500)...
' 良性:' num2str(count_B)...
' 恶性:' num2str(count_M)]);
disp(['测试集病例总数:' num2str(69)...
' 良性:' num2str(number_B)...
' 恶性:' num2str(number_M)]);
disp(['良性乳腺肿瘤确诊:' num2str(number_B_sim)...
' 误诊:' num2str(number_B - number_B_sim)...
' 确诊率p1=' num2str(number_B_sim/number_B*100) '%']);
disp(['恶性乳腺肿瘤确诊:' num2str(number_M_sim)...
' 误诊:' num2str(number_M - number_M_sim)...
' 确诊率p2=' num2str(number_M_sim/number_M*100) '%']);
%% VI. 叶子节点含有的最小样本数对决策树性能的影响
leafs = logspace(1,2,10);
N = numel(leafs);
err = zeros(N,1);
for n = 1:N
t = ClassificationTree.fit(P_train,T_train,'crossval','on','minleaf',leafs(n));
err(n) = kfoldLoss(t);
end
plot(leafs,err);
xlabel('叶子节点含有的最小样本数');
ylabel('交叉验证误差');
title('叶子节点含有的最小样本数对决策树性能的影响')
%% VII. 设置minleaf为13,产生优化决策树
OptimalTree = ClassificationTree.fit(P_train,T_train,'minleaf',13);
view(OptimalTree,'mode','graph')
%%
% 1. 计算优化后决策树的重采样误差和交叉验证误差
resubOpt = resubLoss(OptimalTree)
lossOpt = kfoldLoss(crossval(OptimalTree))
%%
% 2. 计算优化前决策树的重采样误差和交叉验证误差
resubDefault = resubLoss(ctree)
lossDefault = kfoldLoss(crossval(ctree))
%% VIII. 剪枝
[~,~,~,bestlevel] = cvLoss(ctree,'subtrees','all','treesize','min')
cptree = prune(ctree,'Level',bestlevel);
view(cptree,'mode','graph')
%%
% 1. 计算剪枝后决策树的重采样误差和交叉验证误差
resubPrune = resubLoss(cptree)
lossPrune = kfoldLoss(crossval(cptree))
2、随机森林代码
%% I. 清空环境变量
clear all
clc
warning off
%% II. 导入数据
load data.mat
%%
% 1. 随机产生训练集/测试集
a = randperm(569);
Train = data(a(1:500),:);
Test = data(a(501:end),:);
%%
% 2. 训练数据
P_train = Train(:,3:end);
T_train = Train(:,2);
%%
% 3. 测试数据
P_test = Test(:,3:end);
T_test = Test(:,2);
%% III. 创建随机森林分类器
model = classRF_train(P_train,T_train);
%% IV. 仿真测试
[T_sim,votes] = classRF_predict(P_test,model);
%% V. 结果分析
count_B = length(find(T_train == 1));
count_M = length(find(T_train == 2));
total_B = length(find(data(:,2) == 1));
total_M = length(find(data(:,2) == 2));
number_B = length(find(T_test == 1));
number_M = length(find(T_test == 2));
number_B_sim = length(find(T_sim == 1 & T_test == 1));
number_M_sim = length(find(T_sim == 2 & T_test == 2));
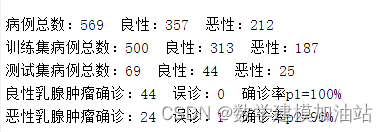
disp(['病例总数:' num2str(569)...
' 良性:' num2str(total_B)...
' 恶性:' num2str(total_M)]);
disp(['训练集病例总数:' num2str(500)...
' 良性:' num2str(count_B)...
' 恶性:' num2str(count_M)]);
disp(['测试集病例总数:' num2str(69)...
' 良性:' num2str(number_B)...
' 恶性:' num2str(number_M)]);
disp(['良性乳腺肿瘤确诊:' num2str(number_B_sim)...
' 误诊:' num2str(number_B - number_B_sim)...
' 确诊率p1=' num2str(number_B_sim/number_B*100) '%']);
disp(['恶性乳腺肿瘤确诊:' num2str(number_M_sim)...
' 误诊:' num2str(number_M - number_M_sim)...
' 确诊率p2=' num2str(number_M_sim/number_M*100) '%']);
%% VI. 绘图
figure
index = find(T_sim ~= T_test);
plot(votes(index,1),votes(index,2),'r*')
hold on
index = find(T_sim == T_test);
plot(votes(index,1),votes(index,2),'bo')
hold on
legend('错误分类样本','正确分类样本')
plot(0:500,500:-1:0,'r-.')
hold on
plot(0:500,0:500,'r-.')
hold on
line([100 400 400 100 100],[100 100 400 400 100])
xlabel('输出为类别1的决策树棵数')
ylabel('输出为类别2的决策树棵数')
title('随机森林分类器性能分析')
%% VII. 随机森林中决策树棵数对性能的影响
Accuracy = zeros(1,20);
for i = 50:50:1000 %模拟从50棵树到1000棵树的一个结果,每次增加50棵 i
%每种情况,运行100次,取平均值
accuracy = zeros(1,100);
for k = 1:100
% 创建随机森林
model = classRF_train(P_train,T_train,i);
% 仿真测试
T_sim = classRF_predict(P_test,model);
accuracy(k) = length(find(T_sim == T_test)) / length(T_test);
end
Accuracy(i/50) = mean(accuracy);
end
% 1. 绘图
figure
plot(50:50:1000,Accuracy)
xlabel('随机森林中决策树棵数')
ylabel('分类正确率')
title('随机森林中决策树棵数对性能的影响')
结果展示
1、决策树
编辑
编辑
编辑
2、随机森林
标签:...,粒子,%%,置信,number,num2str,深度,sim,决策树 From: https://www.cnblogs.com/lovematlab/p/16892976.html