标签：SVM frac matrix geqslant 超平面 mathcal 例题 partial lambda

SVM Summary

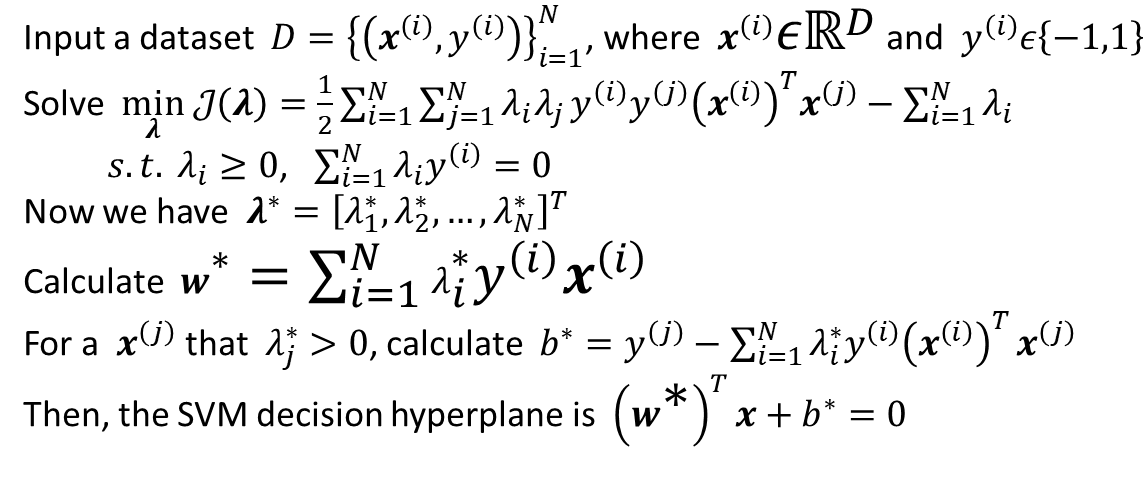
Example

Suppose the dataset contains two positive samples \(x^{(1)}=[1,1]^T\) and\(x^{(2)}=[2,2]^T\), and two negative samples \(x^{(3)}=[0,0]^T\) and \(x^{(4)}=[-1,0]^T\). Please calculate the SVM decision hyperplane.

Calculate

\[\min_\lambda\ {\mathcal{J}(\lambda)} = \frac{1}{2}\sum_{i=1}^N\sum_{j=1}^N \lambda_i\lambda_jy^{(i)}y^{(j)}(x^{(i)})^Tx^{(j)} - \sum_{i=1}^N\lambda_i \]

\[s.t. \ \ \ \ \ \ \ \ \lambda_i \geqslant 0,\ \ \ \ \ \ \sum_{i=1}^N\lambda_iy^{(i)}=0 \]

由\(Dataset\ D:\{x:\{[1,1],[2,2],[0,0],[-1,0]\},y:\{1,1,-1,-1\}\}\)可得下式：

\[\min_\lambda\ {\mathcal{J}(\lambda)} = \frac{1}{2}(2\lambda_1^2+8\lambda_2^2+\lambda_4^2+8\lambda_1\lambda_2+2\lambda_1\lambda_4+4\lambda_2\lambda_4) \\- \lambda_1-\lambda_2-\lambda_3-\lambda_4\\ s.t \ \ \ \ \ \ \ \lambda_1 \geqslant 0,\lambda_2\geqslant 0,\lambda_3\geqslant 0,\lambda_4\geqslant 0\\ \lambda_1+\lambda_2-\lambda_3-\lambda_4 = 0 \]

since \(\lambda_1+\lambda_2 = \lambda_3+\lambda_4 \to \lambda_3 = \lambda_1+\lambda_2 - \lambda_4\):

\[\min_\lambda\ {\mathcal{J}(\lambda)} = \lambda_1^2+4\lambda_2^2+\frac{1}{2}\lambda_4^2+4\lambda_1\lambda_2+\lambda_1\lambda_4+2\lambda_2\lambda_4 - 2\lambda_1-2\lambda_2\\ s.t \ \ \ \ \ \ \ \lambda_1 \geqslant 0,\lambda_2\geqslant 0 \\ \\ \Longrightarrow ^{求偏导}\\ \left\{\begin{matrix} \frac{\partial \mathcal{J}}{\partial \lambda_1} = 2\lambda_1 +4\lambda_2+\lambda_4-2=0 \\ \frac{\partial \mathcal{J}}{\partial \lambda_2} = 4\lambda_1 +8\lambda_2+2\lambda_4-2=0 \\ \frac{\partial \mathcal{J}}{\partial \lambda_4} = \lambda_1 +2\lambda_2+\lambda_4=0 \end{matrix}\right. \]

Lagrange无解，所以极小值在边界上：

• 令\(\lambda_1 = 0， \lambda_3 = \lambda_1+\lambda_2 - \lambda_4\)带入\(\mathcal{J}(\lambda)\)中，得：

\[\mathcal{J}(\lambda) = 4\lambda_2^2+\frac{1}{2}\lambda_4^2++2\lambda_2\lambda_4 -2\lambda_2 \\ \\ \Longrightarrow ^{求偏导}\\ \left\{\begin{matrix} \frac{\partial \mathcal{J}}{\partial \lambda_2} = 8\lambda_2+2\lambda_4-2=0 \\ \frac{\partial \mathcal{J}}{\partial \lambda_4} = 2\lambda_2+\lambda_4=0 \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} \lambda_2=\frac{1}{2} \\ \lambda_4=-1(\le0 \ \ \ \ 不满足s.t.) \end{matrix}\right.\\ 再令：\\ \lambda_2 = 0,则\lambda_4=0， \mathcal{J}(\lambda) = 0；\\ 或\lambda_4 = 0,则\lambda_2=\frac{1}{4}， \mathcal{J}(\lambda) = -\frac{1}{4}； \]

同理可得：

• \(\lambda_2 = 0\)

\[\lambda_1 = 0,则\lambda_4=0， \mathcal{J}(\lambda) = 0；\\ 或\lambda_4 = 0,则\lambda_1=1， \mathcal{J}(\lambda) =-1； \]

• \(\lambda_3 = 0\)

\[\lambda_1 = 0,则\lambda_2=\frac{2}{13}， \mathcal{J}(\lambda) = -\frac{2}{13}；\\ 或\lambda_2 = 0,则\lambda_1=\frac{2}{5}， \mathcal{J}(\lambda) =-\frac{2}{5}； \]

• \(\lambda_4 = 0\)

\[\lambda_1 = 0,则\lambda_2=\frac{1}{4}， \mathcal{J}(\lambda) = -\frac{1}{4}；\\ 或\lambda_2 = 0,则\lambda_1=1， \mathcal{J}(\lambda) =-1； \]

综上：\(\lambda_{1,2,3,4} =\{1,0,1,0\}\)

\[ \left\{\begin{matrix} W=\sum_{i=1}^{N} \lambda_{i} y^{(i)} \boldsymbol{x}^{(i)}\\ b=y^{(j)}-\sum_{i=1}^{N} \lambda_{i} y^{(i)}\left(x^{(i)}\right)^{T} x^{(j)} \end{matrix}\right. \Longrightarrow \left\{\begin{matrix} W = [1,1]^T\\ b=-1 \end{matrix}\right. \\\Longrightarrow x^{(1)}+x^{(2)} -1 =0 \]

标签：SVM,frac,matrix,geqslant,超平面,mathcal,例题,partial,lambda
From： https://www.cnblogs.com/ACxz/p/16886343.html