概率论
1.条件概率
-
\(P (A \cup B) = P(A)+P(B)-P(A \cap B) \le P(A) +P(B)\)
-
条件概率公式 \(P(A|B)=\frac{P(A \cap B)}{P(B)}\)
条件概率:在 \(B\) 事件基础上 \(A\) 发生的概率。公式中相当于把 \(B\) 当做单位 \(1\),在 \(B\) 的空间中看待 \(A\) 的概率。(如下图)
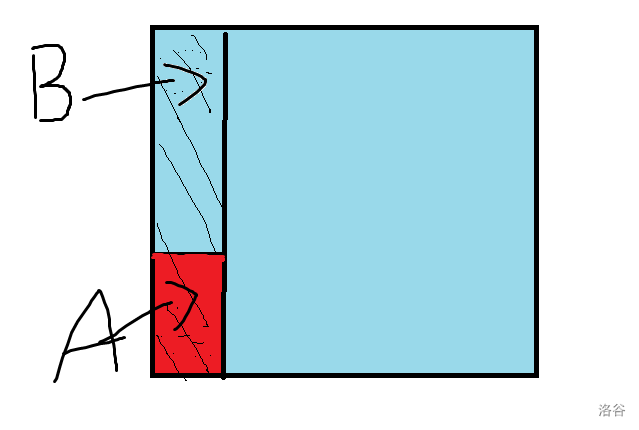
- 对于独立事件 \(A\) 和 \(B\) , \(P(A \cap B) = P(A) \times P(B)\)
- 交换律 \(A \cup B = B \cup A\)
贝叶斯定理
\[\begin{equation}\ P(A|B)=\frac{P(B|A)\times P(A)}{P(B)}\end{equation} \]证明过程:\(P(A \cap B) = P(A|B) \times P(B) = P(B \cap A)=P(B|A)\times P(A)\)
而 \(P(B)=P(B\cap A)+P(B\cap\lnot A)\)
所以此公式的终极形态就是:
\[\begin{equation}P(A|B)=\frac{P(A)\times P(B|A)}{P(A)\times P(B|A)+P(\lnot A)\times P(B|\lnot A)}\end{equation} \]如何从几何意义上理解这个公式?
\(B\) 条件下 \(A\) 发生的概率,相当于在整个概率空间中发生了 \(B\), 且同时发生了 \(A\) 的概率。
公式相当于 \(\frac{部分X}{部分X+部分Y}\) ,其中 \(部分X\) 就是 \(A\cap B\) 。
小例题
已知新冠在人群中发病率 \(0.1\%\) , 核酸检测误判概率为 \(1\%\) ,求证一个人在核酸阳性时真正患病的概率。
解:
可以套用贝叶斯定理,令 \(A\) 为患病, \(B\) 为阳性,则题目所需为 \(P(A|B)\)
由题意知:\(P(A)=0.1\%\) , \(P(\lnot A)=99.9\%\) , \(P(B|A)=99\%\) , \(P(B|\lnot A)=1\%\)
由贝叶斯定理得结果为 \(11/122 \approx 9.6\%\) 。
离散随机变量
随机变量定义
离散随机变量 \(X\) 是一个样本空间到实数的映射,实数作为事件的价值,它就像随机数生成器随机生成的结果。
对于 \(X\) 和 实数 \(x\) ,定义 \(X=x\) 为 \(\{s\in S:X(s)=x\}\) ,即所有标号为 \(x\) 的事件的集合。
譬如,骰子抛出3这个事件就是 \(X=3\)。
\(f(x)=Pr\{X=x\}\) 是 \(X\) 的概率密度函数,满足 \(\sum\limits_xPr\{X=x\}=1\)。
若定义 \(X\) 和 \(Y\) 两个随机变量,则:
\(Pr(x,y)=Pr\{X=x \cap Y=y\}\)
\(Pr(x)=\sum\limits_yPr\{X=x \cap Y=y\}\)
随机变量期望
定义
期望实际就是所有随机变量在样本空间中的平均值,\(X\) 的期望值是:
\[\begin{equation} E[x]=\sum\limits_{x}x\cdot Pr\{X=x\} \end{equation} \]一般用 \(\mu _x\) 表示 \(E[x]\)。
期望的线性性质
\(E[x+y]=E[x]+E[y]\)
即使 \(X,Y\) 不独立,该公式仍然成立
期望与函数
- 若 \(X\) 是随机变量 ,给出任意函数 \(g(x)\) ,定义一个新的随机变量 \(g(X)\) ;若 \(g(X)\) 的期望有定义,则:
- 令 \(g(x)=ax\),则对于任意常数 \(a\),
-
当两个随机变量 \(X,Y\) 独立时:
\[E[XY]=\sum_xPr\{X=x\}\sum_yPr\{Y=y\}=E[x]E[y] \] -
当随机变量 \(X\) 在自然数\(N\) 上取值时,期望计算公式:
\[E[x]=\sum\limits_{i=0}^\infty i\cdot Pr\{X=i\}=\sum\limits_{i=0}^\infty i\cdot (Pr\{X\ge i\}-Pr\{X\ge i+1\})\\=\sum\limits_{i=1}^\infty Pr\{X\ge i\} \]除 \(Pr\{X=0\}\) 外的每个 \(Pr\{X\ge i\}\) 都被加了 \(i\) 次,减了 \(i-1\) 次。
-
凸函数与期望
(下)凸函数定义:
对于任意 \(x,y,\lambda\in[0,1]\), 有 \(f(\lambda x+(1-\lambda y))\le \lambda f(x)+(1-\lambda)f(y)\),则 \(f(x)\) 是凸函数。
假定期望存在且有限,由詹姆斯不等式得:
\[E[f(x)]\ge f(E[x]) \]
方差与标准差
-
方差在数学上表达了一个随机变量可能离均值有多远。均值为 \(E[X]\) 的随机变量的方差为:
\[\begin{align*} Var[X]&=E[(X-E[X])^2]=E[X^2-2E[X]X+E^2[X]]\\&=E[X^2]-2E[E[X]X]+E[E^2[X]] \\&=E[X^2]-2E^2[X]+E^2[X] \\&=E[X^2]-E^2[X] \end{align*} \]注意,由于 \(E^2[X]\) 是实数,所以 \(E[E^2[X]]=E^2[X]\) 。重写上式得到随机变量平方的期望表达式:
\[E[X^2]=Var[X]+E^2[X] \] -
\(X\) 的方差与 \(aX\) 的方差关系为:
- 当 \(X\) 与 \(Y\) 互相独立时:
- 随机变量 \(X\) 的方差是 \(\sqrt{Var[x]}\)
概率期望练习
\(C3-1\)
抛出两枚骰子,其中较大值的期望为多少?
solution: 设最大值为 \(i\) , 则两个值都在 \(1\to i\) 的概率为 \((\frac{i}{6})^2\) ,两个都在 \(1\to i-1\) 的概率为 \((\frac{i-1}{6})^2\) ,则其中至少有一个是 \(i\) 的概率就是 \((\frac{i^2-(i-1)^2}{36})=\frac{i*2-1}{36}\) ,故期望为 \(\sum\limits_{i=1}^6\frac{i*(2*i-1)}{36}\)。
\(C3-3\)
有 \(3\) 枚骰子,选择一个点数并抵押 \(1\) RMB,三个骰子中有 \(k\) 个与所选点数相同,则奖励 \(k\) 人民币,若 \(k=0\) ,则输掉自己的 \(1\) RMB,问期望收入。
solution: 假设有 \(i\) 个骰子猜中,则一共有 \(3\choose{i}\) 种情况,概率为 \((\frac{1}{6})^i(\frac{5}{6})^{3-i}\) ,结果就是 \({\sum\limits_{i=1}^{3}}i{{3}\choose{i}}(\frac{1}{6})^i(\frac{5}{6})^{3-i}\)
\(C3-6\)
\(X\) 是非负随机变量,且 \(E[X]\) 有定义,对于任何 \(t\in(0,+\infty]\) 证明马尔可夫(Markov)不等式 :
\[Pr\{X\ge t\} \le E[X]/t \]solution:
\[\begin{align*} E[X]&=\sum\limits_{i=0}^\infty i\cdot Pr\{X=i\}\\ &\ge \sum\limits_{i=t}^\infty i \cdot Pr\{X=i\}\\ &\ge \sum\limits_{i=t}^\infty t \cdot Pr\{X=i\}\\ &=t\cdot Pr\{X\ge t\} \end{align*} \]Markov 不等式可以松散地确定尾部事件的概率上界,一个直观的例子是:假如一公司的平均工资是 \(\mu\) ,则工资高于 \(n\cdot \mu\) 的人数不超过 \(\frac{1}{n}\) 。
切比雪夫(chebyshev)不等式,对于任意 \(d>0\) ,有两种形式:
\[Pr\{|X-\mu_x|\ge d\} \le \frac{Var[X]}{d^2} \\ Pr\{|X-\mu_x|\ge \sigma d\} \le \frac{1}{d^2} \]可用Markov 不等式证明它的各种形式:
\[Pr\{|X-\mu_x|\ge d\} = Pr\{|X-\mu_x|^2\ge d^2\} \le \frac{E[(X-E[X])^2]}{d^2} =\frac{Var[X]}{d^2}\\ Pr\{|X-\mu_x|\ge \sigma d\} =Pr\{|X-\mu_x|^2\ge \sigma^2d^2\} \le \frac{E[(X-\mu_x)^2]}{\sigma^2d^2}=\frac1{d^2} \]第二种形式表明,随机变量距离期望值有至少 \(d\) 个标准差的概率不超过 \(\frac1{d}\),这表明随机变量多分布于期望值附近。
\(C3-8\)
比较 \(E[X]^2\) 和 \(E[X^2]\) 大小。
solution:
\(E[X^2]-E[X]^2=Var[X]\ge 0\)
\(C3-9\)
若 \(X\) 取值仅为 \(0\) 或者 \(1\),证明: \(Var[X]=E[X]\cdot E[1-X]\)
solution:
\[f(0)=E[1-X],f(1)=E[X],f(0)+f(1)=1\\ \begin{align*} \sigma^2(X)&=f(0)(0-E[X])^2+f(1)(1-E[X])^2\\ &=f(0)E^2[X]+f(1)E^2[X]-2f(1)E[X]+f(1)\\ &=E^2[X]-2E^2[X]+E[X]\\ &=E[X]- E^2[X]=E[X](1-E[X])\\ &=E[X]\cdot E[1-X] \end{align*} \]通过方差与期望平方的关系,还有更优雅的方法: \(X^2=X\)
\[\begin{align*} Var[X]&=E[X^2]-E^2[X]\\ &=E[X]-E^2[X]\\ &=\dots \end{align*} \]$ C3-10$
证明:\(Var[aX]=a^2Var[X]\)
solution:
\[Var[aX]=E[a^2X^2]-E^2[ax]=a^2E[X^2]-a^2E^2[X]=a^2Var[X] \]几何分布与二项分布
几何分布
定义:
相同条件下互相独立进行多次实验,\(k\) 次才获得成功,则 \(k\) 与其概率满足几何分布;
\(p\) 为成功概率, \(q=1-p\) 为失败概率。
期望:
\(E[X]=\sum\limits_{k=1}^\infty kq^{k-1}p =\frac{p}{q}\sum\limits_{k=0}^\infty kq^k = \frac pq \cdot \frac{q}{(1-q)^2}=\frac pq \cdot \frac q{p^2}=\frac 1p\)
方差:
未完待续
标签:Pr,frac,sum,教学,ge,保姆,Var,概率论,随机变量 From: https://www.cnblogs.com/subtlemaple/p/16618339.html