研究生考试中图论中求解最短路径的算法主要有两种,Dijkstra算法及Floyd算法,其中Dijkstra算法用于求解单源最短路径问题,而Floyd算法则用于解决多源最短路径问题。本文对这两种算法做一总结。
Dijkstra算法
Dijkstra算法是最经典的最短路径算法,这是一种典型的贪心算法,不过可以证明,这种贪心策略得到的就是全局最优解。Dijkstra算法的详细描述可以参考数据结构的基础书籍,以下文章也可供参考:
Dijkstra 算法的主要思想可以简要总结为:
- 将所有顶点分为两类,即
Known和Unknown两个集合,初始时所有顶点均位于Unknown集合中,算法的目标就是将Unknown集合中的所有顶点移至Known集合中; - 每一个顶点均有一个表示当前状态的属性表,其中一定要有一个变量记录此时距离源点的最短路径长度(不妨将其记为
dr),除此之外根据需要还可以有一些附加信息,如最短路径来源顶点、经过的顶点数、所属的集合(Known还是Unknown)等; - 初始时,源点的
dr为0,其余所有顶点的dr均为无穷大,这里的无穷大只是数学上的说法,实际编程中会用一个合适的值替代; - 从
Unknown集合中选出dr最小的一个顶点,将其移至Known集合中,并更新Unknown集合中剩余顶点的dr; - 重复第4步,直至
Unknown为空。
算法的核心就是上述步骤中的第4步,这里所谓的更新是指:遍历与选出的顶点邻接的所有顶点,若其位于Unknown集合中,比较当前dr与经由选出顶点至其的距离,若新的距离小于dr,则使用新的距离替代dr*。需要注意的是,*这里只更新比较位于Unknown集合中的邻接顶点,不需要去更新Known集合中的顶点,否则这就不是贪心法了。
用一张图可以很好的说明以上步骤:
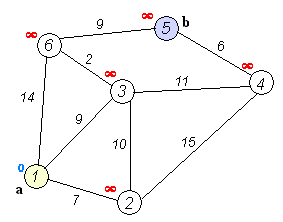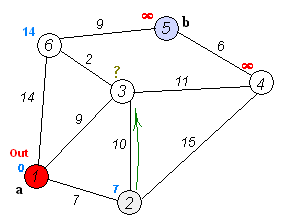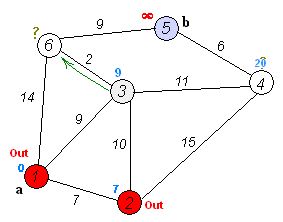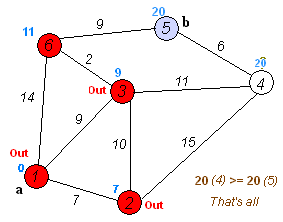
下面给出Dijkstra算法的核心伪代码:
void Dijkstra() {
while (!Unknown.empty()) {
V = Unknown.FindMinDr();
Unknown.remove(V);
Known.add(V);
foreach (W adjacent to V) {
if (Known.contain(W))
continue;
if (V.dr + D[v][w] < W.dr) {
W.dr = V.dr + D[v][w];
}
}
}
}
Dijkstra算法的结果一般使用一个一维表(即数组)来记录,每一项即是一个顶点对应的当前状态属性表。算法的复杂度取决于具体实现方式,一个较好的选择是使用斐波那契堆来实现,不过粗略的看,其复杂度大概是 \(O(n^2)\) 级别的。如果使用优先队列则可压缩到 \(O((m+n)log_2n)\)
Floyd算法
Floyd算法的实质是一种动态规划算法,最初不允许经由任何中间点,之后逐步添加允许的中间点,可以证明,最终允许的中间点为全部顶点时,算法得出的就是最优解。算法详细描述可见:
Floyd算法的核心伪代码如下:
// N : 顶点数
// D[N][N] : 两点间最短距离记录
void Floyd() {
for (k = 0; k < N; k++) {
for (i = 0; i < N; i++) {
for (j = 0; j < N; j++) {
if (D[i][j] > D[i][k] + D[k][j]) {
D[i][j] = D[i][k] + D[k][j];
}
}
}
}
}
最外层的for循环逐渐添加允许途径的中间点,内层的两个循环遍历所有点之间的距离。Floyd算法的结果一般使用一个二维表(即二维数组)来记录,即上述代码中的D[N][N],初始值即为当前图的邻接矩阵(Adjacency Matrix)表示。算法的复杂度是 \(O(n^3)\)的。