考研排序复习笔记
-
插入排序
#include<stdio.h>
#include<stdlib.h>
#define MaxSize 9
//折半插入排序
void ZBInsertSort(int A[],int n){
int i,j,high,low,mid;
for(i=2;i<=n;i++){
A[0] = A[i];
low = 1;high = i-1;
while(low<=high){
mid=(low+high)/2;
if(A[mid]>A[0]){
high=mid-1;
}
else{
low = mid+1;
}
}
for(j = i-1;j>=high+1;--j){
A[j+1] = A[j];
}
A[high+1] = A[0];
}
}
//直接插入排序(带哨兵)
void InsertSort(int A[],int n){
int i,j;
for(i=2;i<=n;i++){
if(A[i]<A[i-1]){
A[0] = A[i];
for(j =i-1;A[0]<A[j];j--){
A[j+1] = A[j];
}
A[j+1] = A[0];
}
}
}
//插入排序的复杂度都是O(n^2)
int main(){
int A[] = {0,49,38,65,97,76,13,27,49};
for(int i = 1;i<MaxSize;i++){
printf("%d ",A[i]);
}
ZBInsertSort(A,8);
printf("\n");
for(int i = 1;i<MaxSize;i++){
printf("%d ",A[i]);
}
return 0;
}
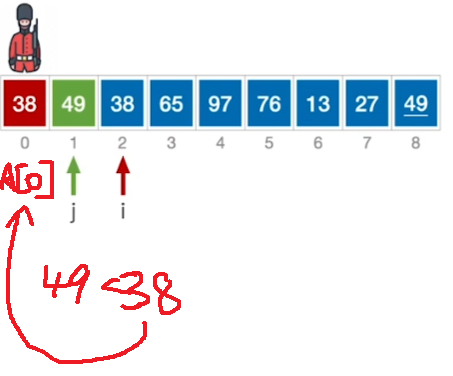

空间复杂度:\(O(1)\)
平均时间复杂度\(:O(n^2)\)
相当于从A[2]一路顺序查找下去,是A[1]往后逐渐有序。
开始后A[1]----A[2]----是有序的
这部分可以使用折半查找
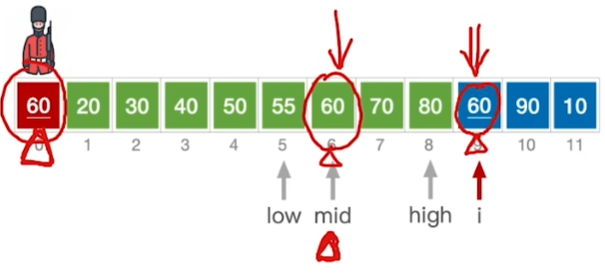
复习折半查找的停止条件:low>high
-
A[0]>mid
- 数在mid后面,low = mid + 1
-
A[0]<mid
- 说明数在mid前面部分,high = mid - 1
-
希尔排序(Shell Sort)
灵感来源:插入排序在基本有序的情况下表现很好
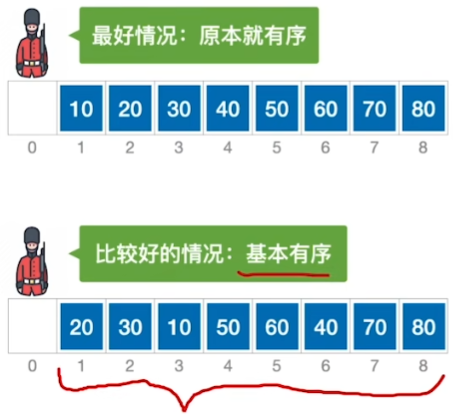
所以希尔排序的思想是基于这种基本有序
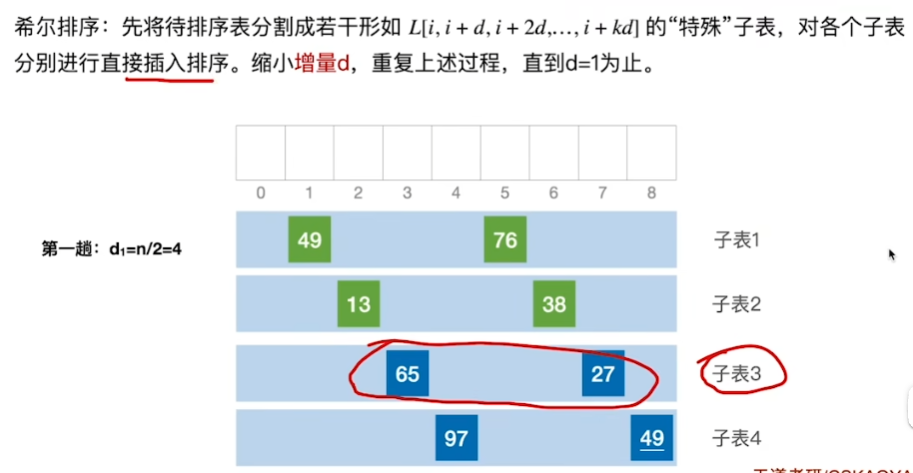


希尔排序代码实现
#include<stdio.h>
#include<stdlib.h>
#define MaxSize 9
//希尔排序
//往后逐个对比
void ShellSort(int A[],int n){
int d,i,j;
for(d = n/2;d>=1;d = d/2){
for(i=d+1;i<=n;++i){
if(A[i]<A[i-d]){
A[0] = A[i];
for(j=i-d;j>0 && A[0]<A[j];j-=d)
A[j+d] = A[j];
A[j+d] = A[0];
}
}
}
}
//希尔排序
//一串捋直了再下一串
void testShellSort(int A[],int n){
int d,i,j;
for(d = n/2;d>=1;d=d/2){ //步长变化
for(i=1;i<=d;i++){ //多少组
for(i=d+1;i<=n;i+=d){ //遍历每一组的所有数字
if(A[i] < A[i-d]){
A[0] = A[i]; //小的放在A[0]
for(j=i-d;j>0 && A[0]<A[j];j-=d){
A[j+d] = A[j];
}
A[j+d] = A[0];
}
}
}
}
}
//插入排序的复杂度都是O(n^2)
int main(){
int A[] = {NULL,49,38,65,97,76,13,27,49};
for(int i = 1;i<MaxSize;i++){
printf("%d ",A[i]);
}
testShellSort(A,8);
printf("\n");
for(int i = 1;i<MaxSize;i++){
printf("%d ",A[i]);
}
return 0;
}
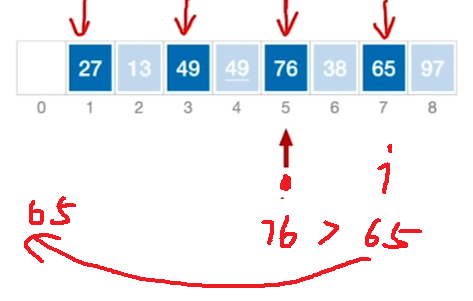
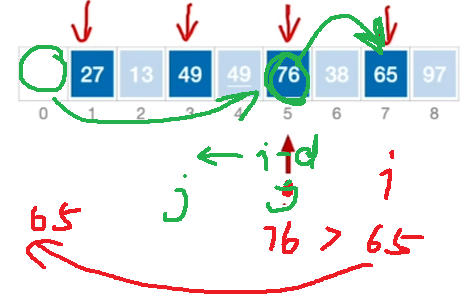
以上第一种是:i++,逐个逐个比较各自的串
第二种是 只扫描A[0] -> A[1] ->A[2]->>>一个d,在每次扫描到一个串的时候完成这个串的排序
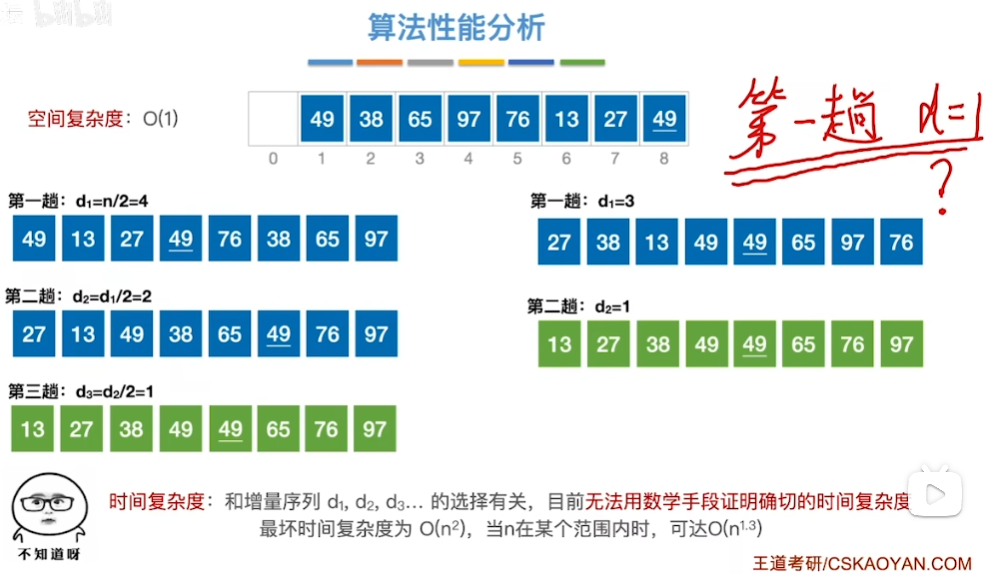
\(空间复杂度为O(1)\)
\(时间复杂度与选取的d挂钩\)
当第一次选取d=1时,希尔排序 退化为 插入排序
稳定性分析: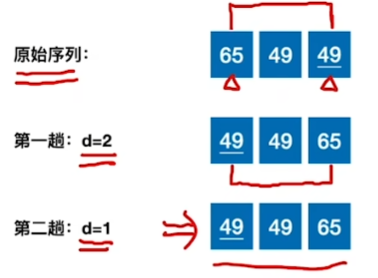
稳定性:不稳定
且只使用于顺序表,不使用于链表
-
冒泡排序(Bubble Sort)
基于交换的排序:根据序列中两个元素的关键字的比较结果来对换两个记录在序列中的位置
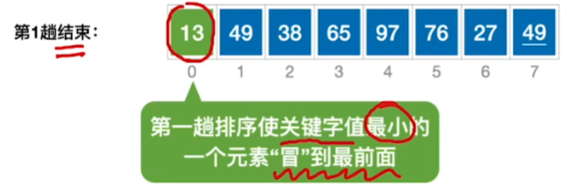
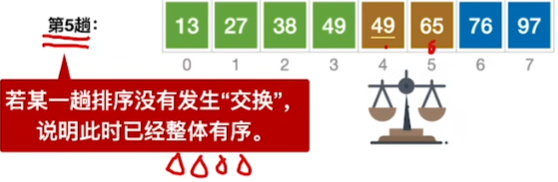
当最后一趟没有任何交换时,说明已经有序了
#include<stdio.h>
#include<stdlib.h>
void swap(int &a,int &b){
int temp;
temp = a;
a = b;
b = temp;
}
//MM手写版 version.1
void BubbleSort(int A[],int n){
for(int i=1;i<=n-1;i++){
bool flag = false;
for(int j=n-1;j>=i;j--){ //犯错1:int j=n-1;j=i;j-- 每次判断的时候都会重新定义j导致永远退不出循环!
if(A[j]<A[j-1]){
swap(A[j],A[j-1]);
flag = true;
}
}
if(flag == false){ //犯错2:if flag == false 太粗心!
break;
}
}
}
// mm手写版与王道给的基本一致
//王道版
void WD_BubbleSort(int A[],int n){
for(int i=0;i<n-1;i++){ //交换的趟数 = n-1
bool flag = false; //表示本趟冒泡是否发生交换的标志
for(int j=n-1;j>i;j--){ //一趟冒泡
if(A[j-1] > A[j]){ //若为逆,则交换
swap(A[j-1],A[j]);
flag = true;
}
}
if(flag == false){ //本趟遍历之后如果没有发生交换,则已经有序
break;
}
}
}
int main(){
int list[] = {49,38,65,97,76,13,27,49};
for(int i = 0;i<=7;i++){
printf("%d ",list[i]);
}
printf("\n");
BubbleSort(list,8);
for(int i = 0;i<=7;i++){
printf("%d ",list[i]);
}
printf("\n");
return 0;
}
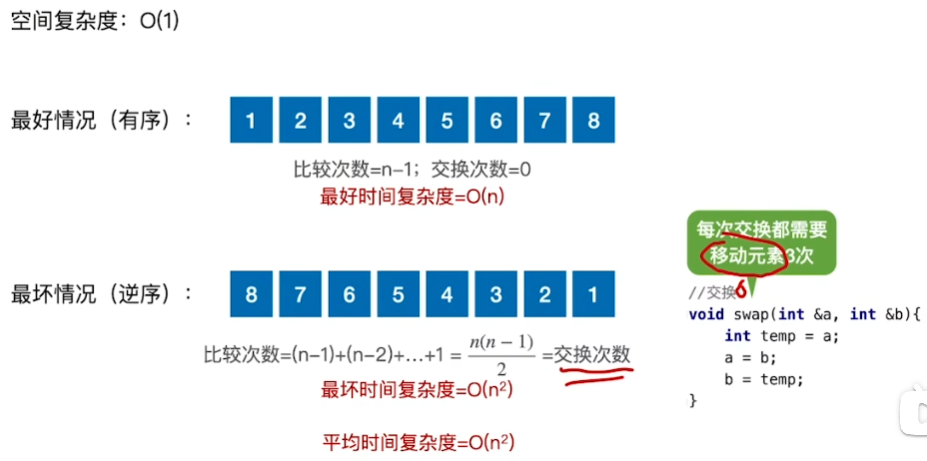
冒泡排序显然是稳定的
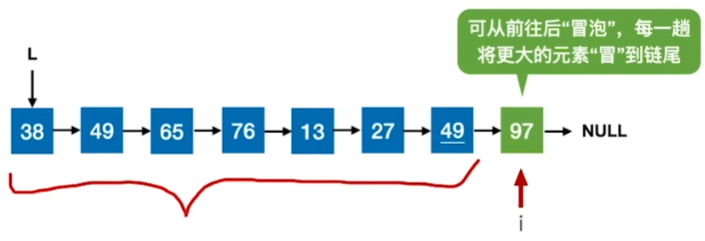
且适用于链表
代码给的是从后往前冒,其实从前往后也是可以的所以要注意题目给的条件
易忘点:如果一趟排序过程未发生“交换”,则可以提前结束
-
快速排序
如名字所言:确实是最厉害的
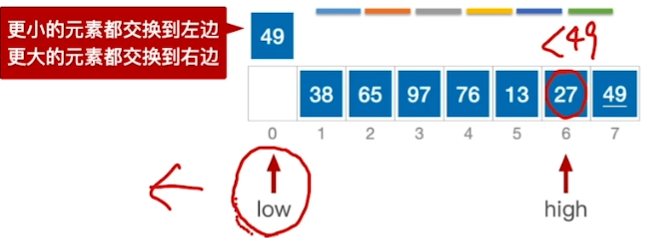
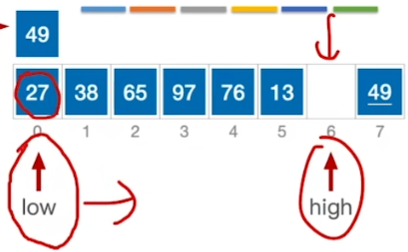
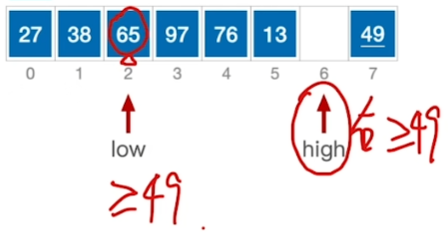
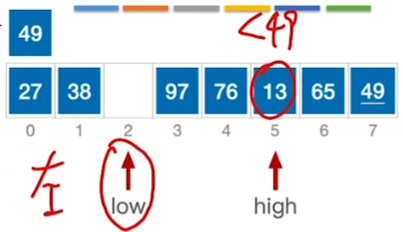
核心思想:
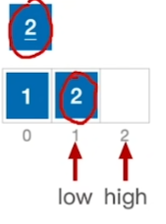
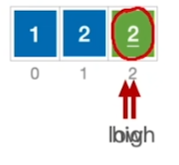
\(high所指的>基准:high--\)
\(high所指 < 基准:放到low那里\)
\(low所指 < 基准:low++\)
\(low所指 > 基准:放到high那里\)
终止条件: \(low == high\)
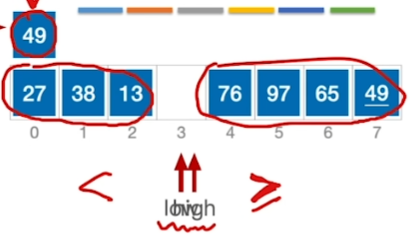
于是划分为$$【<A】 | 【A】 | 【>A】$$
再分别在两边重复以上过程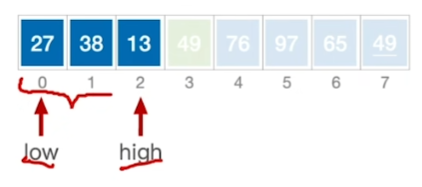
#include<stdio.h>
#include<stdlib.h>
//Partition (分割)
int Partition(int A[],int low,int high){
int pivot = A[low]; //pivot:枢轴
while(low < high){
while(low<high && A[high] >=pivot) --high; //high前推找比pivot小的
A[low] = A[high];
while(low<high && A[low] <=pivot) ++low; //low后推找比pivot大的
A[high] = A[low];
}
A[low] = pivot;
return low;
}
void QuickSort(int A[],int low,int high){
if(low<high){ //递归跳出的条件
int pivotpos = Partition(A,low,high); //划分
QuickSort(A,low,pivotpos-1); //划分左子表
QuickSort(A,pivotpos+1,high); //划分右子表
}
}
int main(){
int list[] = {49,38,65,97,76,13,27,49};
for(int i = 0;i<=7;i++){
printf("%d ",list[i]);
}
printf("\n");
QuickSort(list,0,7);
for(int i = 0;i<=7;i++){
printf("%d ",list[i]);
}
printf("\n");
return 0;
}

空间复杂度:

其实分析起来
本质上就像一个二叉树
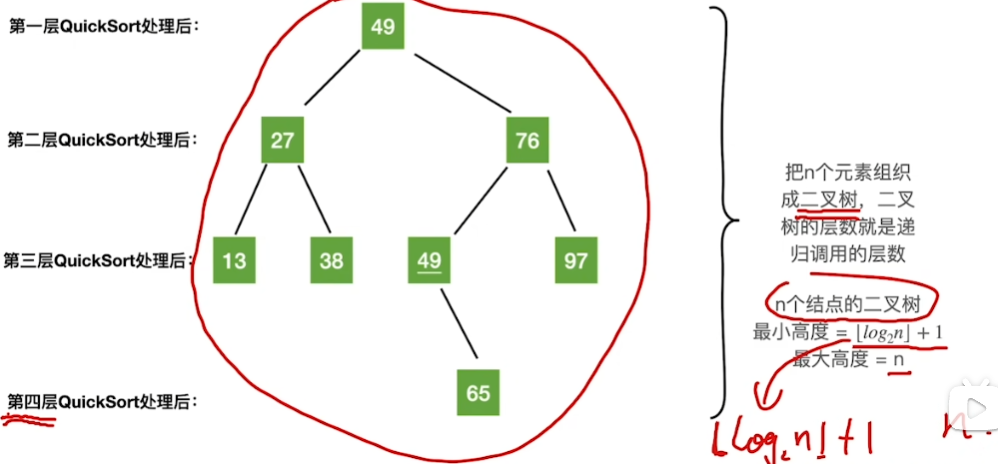
最好/最坏情况分析:
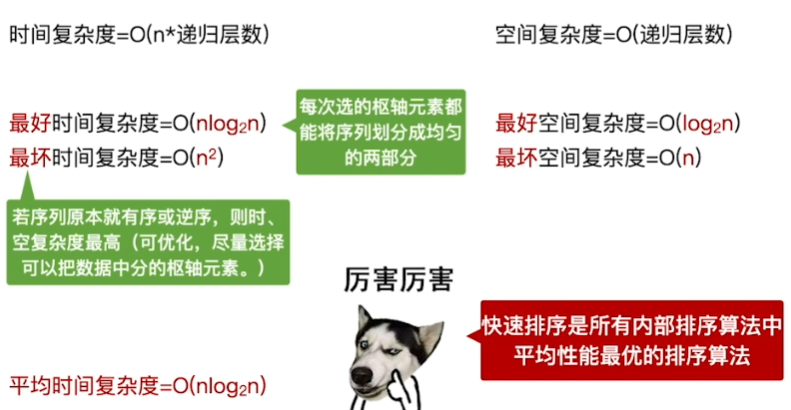
快速排序的稳定性:不稳定!
-
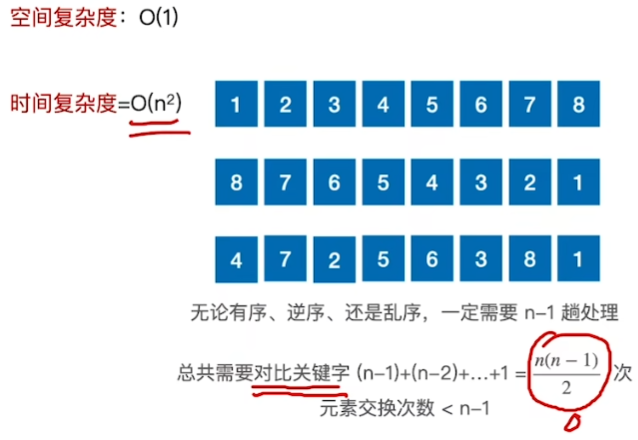
简单选择排序
从头到尾扫描 1 次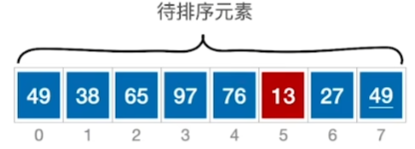 然后交换位置
然后交换位置
从头到尾扫描 2 次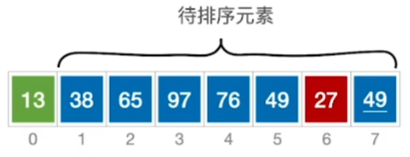 然后交换位置
然后交换位置
从头到尾扫描 3 次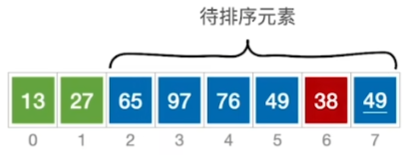 然后交换位置
然后交换位置
\(n个元素的简单排序需要处理n-1趟\)
代码实现:
#include<stdio.h>
#include<stdlib.h>
void swap(int &a,int &b){
int temp;
temp = a;
a = b;
b = temp;
}
//MM手写版 version.1
//王道版交换的是index,我交换的是数据
void SelectSort(int A[],int n){
for(int i=0;i<n;i++){ //需要排n-1次 *error:i<n-1就行了 因为n=8,最后一个元素实际下标是7
int min = A[i];
for(int j=i;j<n;j++){ //逐行扫描
if(A[j]<min){
swap(min,A[j]);
}
}
A[i] = min;
}
}
//王道版 简单选择排序
void WD_SelectSort(int A[],int n){
for(int i=0;i<n-1;i++){ //一共排n-1趟
int min = i; //记录最小元素位置
for(int j=i+1;j<n;j++)
if(A[j]<A[min]) min=j; //更新最小元素位置
if(min != i) swap(A[i],A[min]);
}
}
int main(){
int list[] = {49,38,65,97,76,13,27,49};
for(int i = 0;i<=7;i++){
printf("%d ",list[i]);
}
printf("\n");
WD_SelectSort(list,8);
for(int i = 0;i<=7;i++){
printf("%d ",list[i]);
}
printf("\n");
return 0;
}
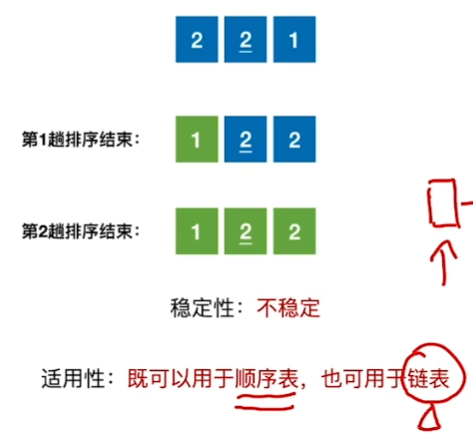
可以使用链表来练练手!
-
堆排序(Heap Sort)
定义:
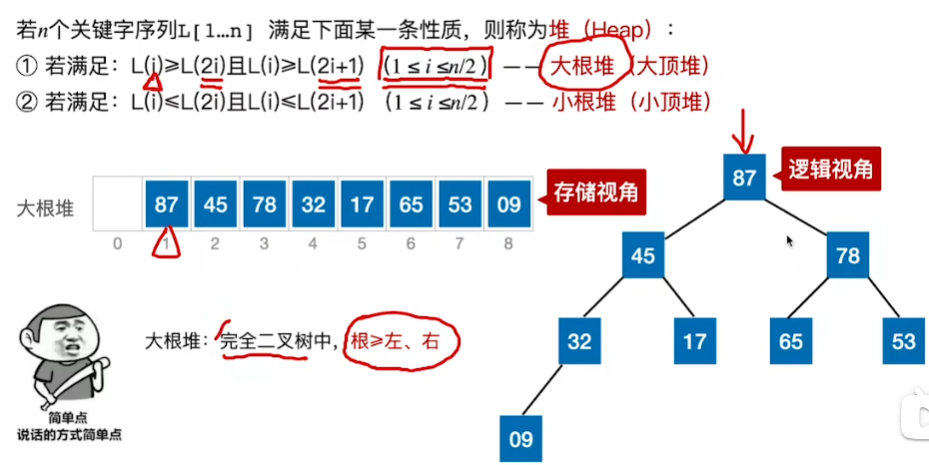
在顺序存储的完全二叉树中,非终端节点编号 i<=[n/2]
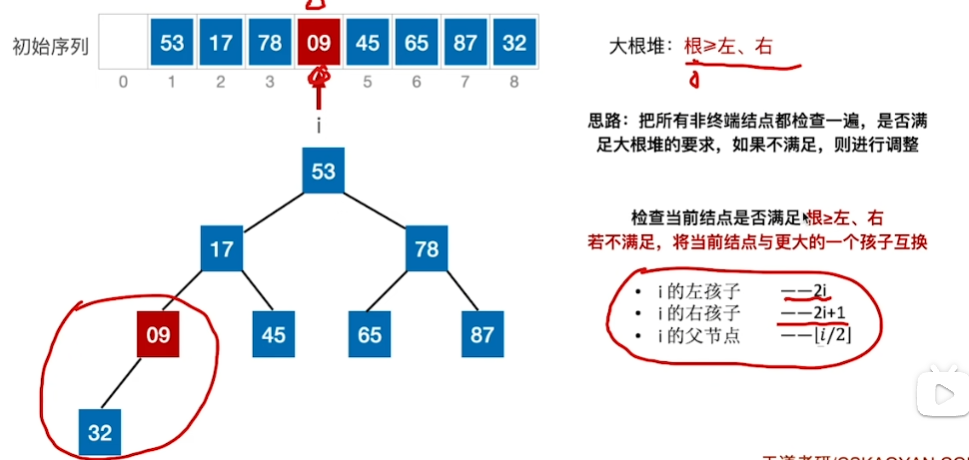
先找到 [8/2] == 4 也就是为A[4]这个结点,查看是否满足根<=左右
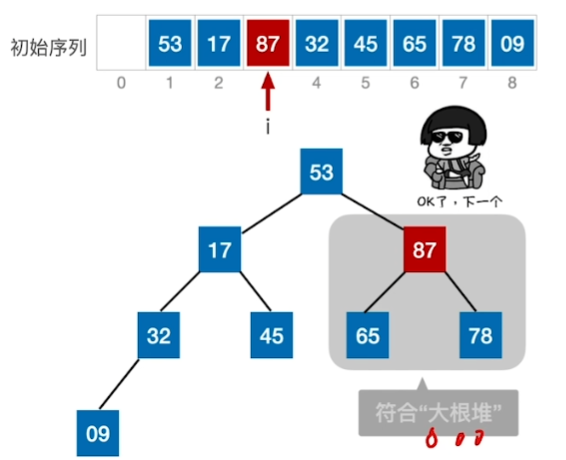
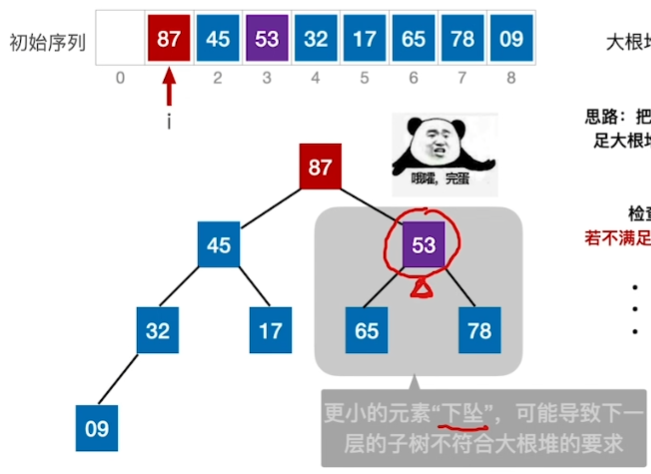
53这个结点下坠后,导致下一层子树不符合大根堆,还需再调整(即小元素不断“下坠”)
得到这样一个完整的大根堆之后
踢出最大的87,即将A[0]与最后一个互换
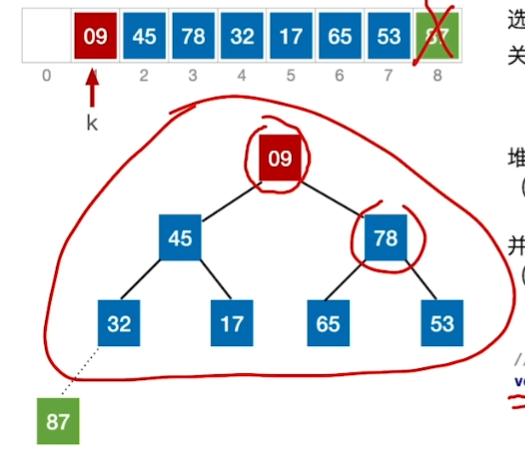
蓝色部分失去大根堆特性,继续重复步骤,变成大根堆,再交换一次
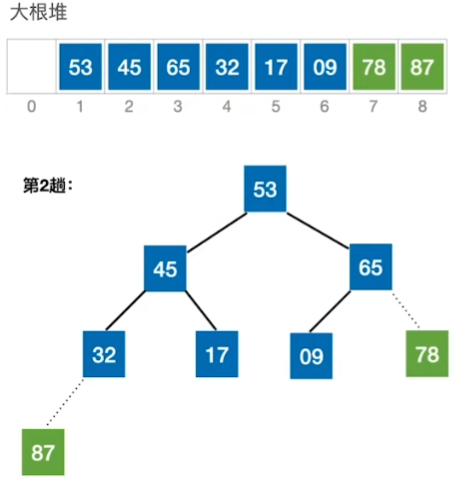
重复以此步骤: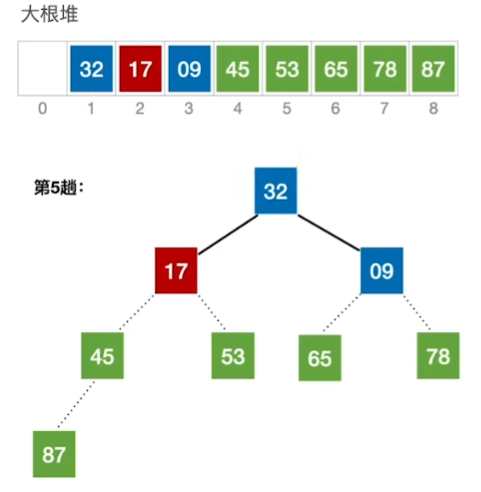
代码实现:
#include<stdio.h>
#include<stdlib.h>
void swap(int &a,int &b){
int temp;
temp = a;
a = b;
b = temp;
}
//将以k为根的子树调整为大根堆
void HeadAdjust(int A[],int k,int len){
A[0] = A[k]; //A[0]暂存子树的根结点
for(int i=2*k;i<=len;i*=2){ //沿key较大的子节点向下筛选
if(i<len && A[i]<A[i+1])
i++;
if(A[0]>=A[i]){
break;
}
else{
A[k] = A[i];
k=i;
}
}
A[k] = A[0];
}
//建立大根堆
void BuildMaxHeap(int A[],int len){
for(int i=len/2;i>0;i--){ //从后往前调整非终端结点
HeadAdjust(A,i,len);
}
}
void HeapSort(int A[],int len){
BuildMaxHeap(A,len);
for(int i=len;i>1;i--){ //i=len 指向待排序元素序列的最后一个(堆底元素)
swap(A[i],A[1]);
HeadAdjust(A,1,i-1);
}
}
int main(){
int list[] = {NULL,53,17,78,9,45,65,87,32};
for(int i = 1;i<=8;i++){
printf("%d ",list[i]);
}
printf("\n");
HeapSort(list,8);
for(int i = 1;i<=8;i++){
printf("%d ",list[i]);
}
printf("\n");
return 0;
}

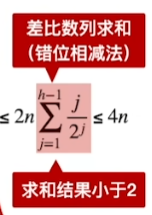 建堆的过程,关键字对比次数不超过4n,建堆时间复杂度=O(n)
建堆的过程,关键字对比次数不超过4n,建堆时间复杂度=O(n)
堆排序的稳定性:
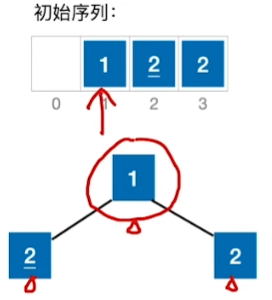
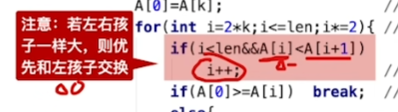
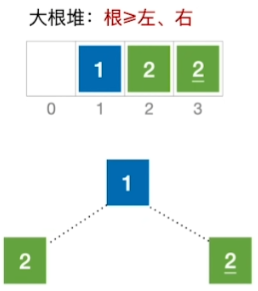
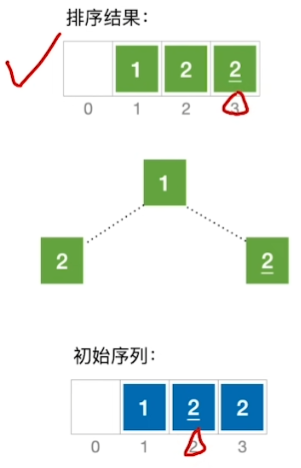
结论:堆排序是不稳定的
-
归并排序(Merge Sort)
Merge:归并、合并
把两个或多个已经有序的序列合并成一个
一般采用2路归并

A[]是原本需要排序的数组
先定义空数组B[],然后第一个for循环把A数组复制到B数组
用 i,j 分别放在两个low--mid,mid+1--high两个有序数组上
依次对比
更新A[]
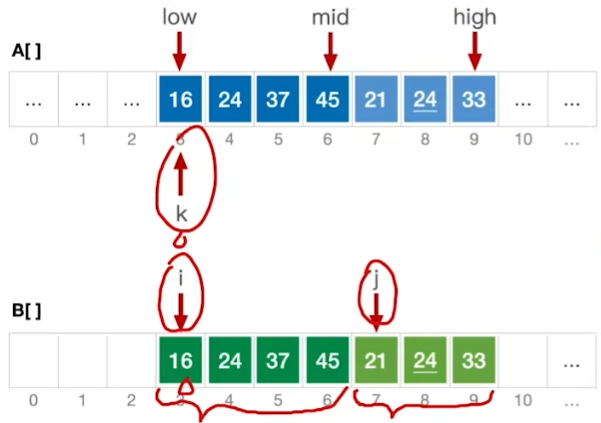
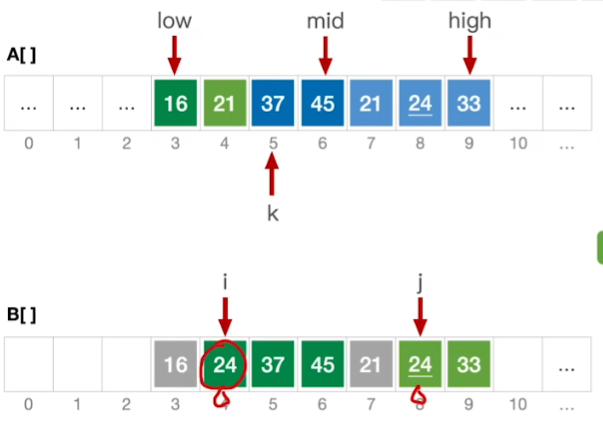
如上图: 在复制完数组后
for 后面 写的是 i=low,j=mid+1,k=low
for的结束条件是i,j越界 即:i<=mid和j<=high
实现思路:
用MergeSort递归调用,将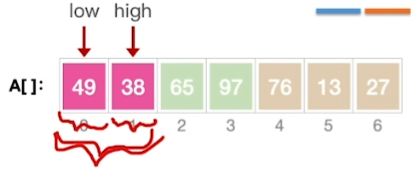
递归到最底层将两个个数为1的子序列看成两路
做排序
再一步一步往大了的去排序
#include<stdio.h>
#include<stdlib.h>
int *B = (int *)malloc(7*sizeof(int)); //定义辅助数组B
//A[low..mid]和A[mid+1...high]各自有序,将这两个部分归并
void Merge(int A[],int low,int mid,int high){
int i,j,k;
for(k = low;k<=high;k++)
B[k] = A[k];
for(i = low,j = mid+1,k=i;i<=mid && j<=high;k++){
if(B[i]<=B[j])
A[k] = B[i++]; //将较小的值复制到A中
else
A[k] = B[j++];
}
while(i<=mid) A[k++] = B[i++];
while(j<=high) A[k++] = B[j++];
}
void MergeSort(int A[],int low,int high){
if(low<high){
int mid=(low+high)/2; //从中间划分
MergeSort(A,low,mid); //左半部分归并
MergeSort(A,mid+1,high); //右半
Merge(A,low,mid,high); //归并
}
}
int main(){
int A[] = {49,38,65,97,76,13,27};
for(int i = 0;i<=6;i++){
printf("%d ",A[i]);
}
printf("\n");
MergeSort(A,0,6);
for(int i = 0;i<=6;i++){
printf("%d ",A[i]);
}
printf("\n");
free(B);
return 0;
}
归并树 类似于 倒立的二叉树
-
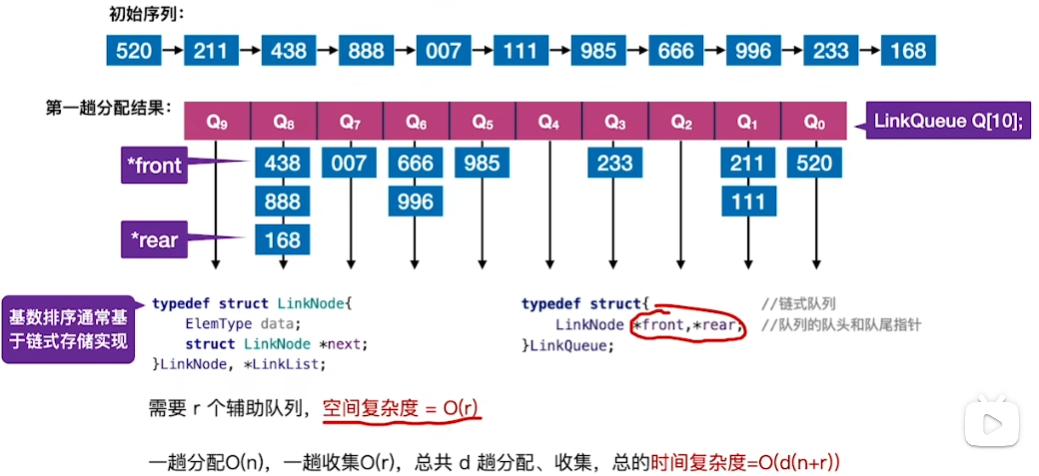
基数排序(Radix Sort)

关键字位 权重递增的次序

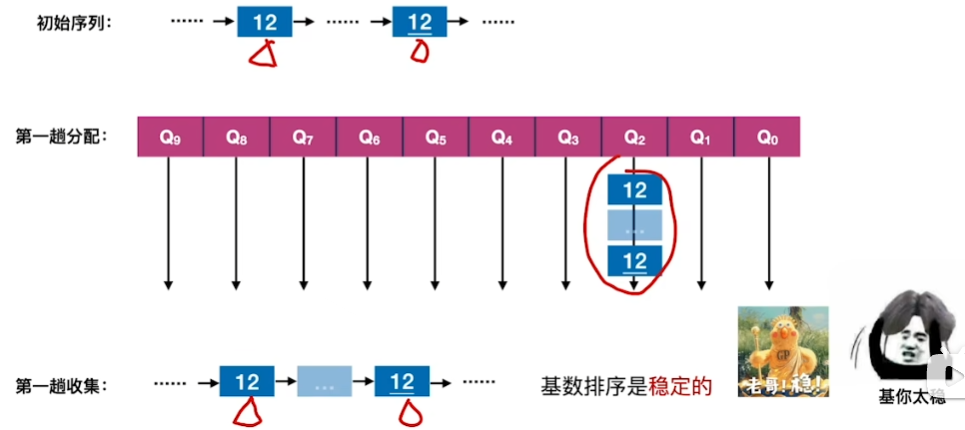 基你太稳!
基你太稳!
基你太稳
基数排序的适用场景:

以上就是所有的内部排序:
- 插入排序
- 直接插入排序
- 希尔排序
- 选择排序
- 简单选择排序
- 堆排序
- 交换排序
- 冒泡排序
- 快速排序
- 归并排序
- 基数排序