已知一个长度为 \(n\) 的序列 \(a\),共有 \(m\) 次操作,每次操作如下:
- 将某区间每一个数加上 \(k\)。
- 求出某区间每一个数的和。
之前学过一个算法叫做树状数组,它的本质就是将一个 \([1,x]\) 的区间二进制拆分装化成若干个区间,数组里的每一个元素都代表每一个区间。若需要将 \(x\) 修改只需要将 \(x\) 的父亲节点的元素修改即可,查询就是将区间拆分即可。这样可以在 \(O(\log_2n)\) 的时间复杂度来实现“单点修改,区间查询”或“区间修改,单点查询”的操作。
这一题的类型属于“区间修改,区间查询”,对于这种类型的题,我们很快就会想到一种 \(O(mn\log_2n)\) 的做法对于每一次修改,暴力枚举区间的所有值,将其一一修改,变成“单点修改,区间查询”。或者对于每一次查询暴力查询每一个元素,累加总和,变成“区间修改,单点查询”,但是这些时间复杂度都不够优秀,接下来引入一个更优秀的数据结构叫做——线段树。
线段树顾名思义就是有一堆线段的树,它的根节点的编号为 \(1\) 区间为 \([1,n]\)。线段树里每一个元素的子节点(除叶子节点外)都是将这个区间分成两半。
比如区间 \([l,r]\) 的子节点如下计算:
令 \(mid=\lfloor\frac{l+r}{2}\rfloor\),则区间 \([l,r]\) 的两个子节点分别为 \([l,mid]\) 和 \([mid+1,r]\)。
由此我们可以得出 \(n=6,a=\{1,2,3,4,5,6\}\) 的线段树的样子。
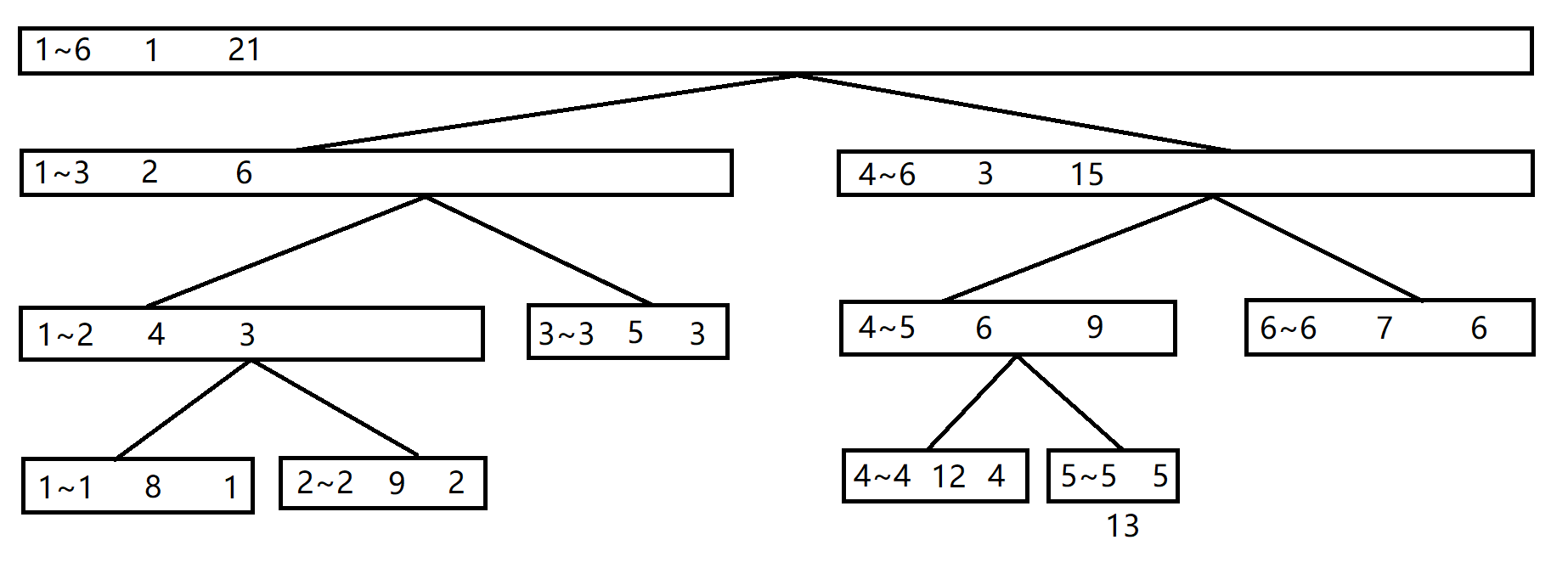
(元素里前两个数表示区间,第三个数表示编号,第四个数表示总和)
从此图我们可以想出构造线段树的方法:
- 从根节点开始递归,每次递归到叶子节点(即 \(l=r\) 时)将叶子节点的元素值设为原数组的值。
- 回溯时,将遍历到的节点的儿子节点的元素值合并到这个节点即可。
在这里我们定义一个无返回值的函数 \(\text{push_up}(x)\) 表示将节点 \(x\) 的儿子节点的值合并传入节点 \(x\)。
构造线段树代码如下:
void push_up(int u) {
sum[u] = sum[u << 1] + sum[u << 1 | 1];
} // 将叶子节点的和传入此节点
void build(int u, int l, int r) {
if (l == r) {
sum[u] = a[l];
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
push_up(u);
}
注意由于线段树的存储方式是用树来存的,所以我们用来存线段树的数组需要开 \(4\) 倍空间。
如果我要查询区间和怎么办呢?
举个栗子,若我们要查询 \([3,5]\) 的区间和我们会从区间 \([1,6]\) 开始遍历。
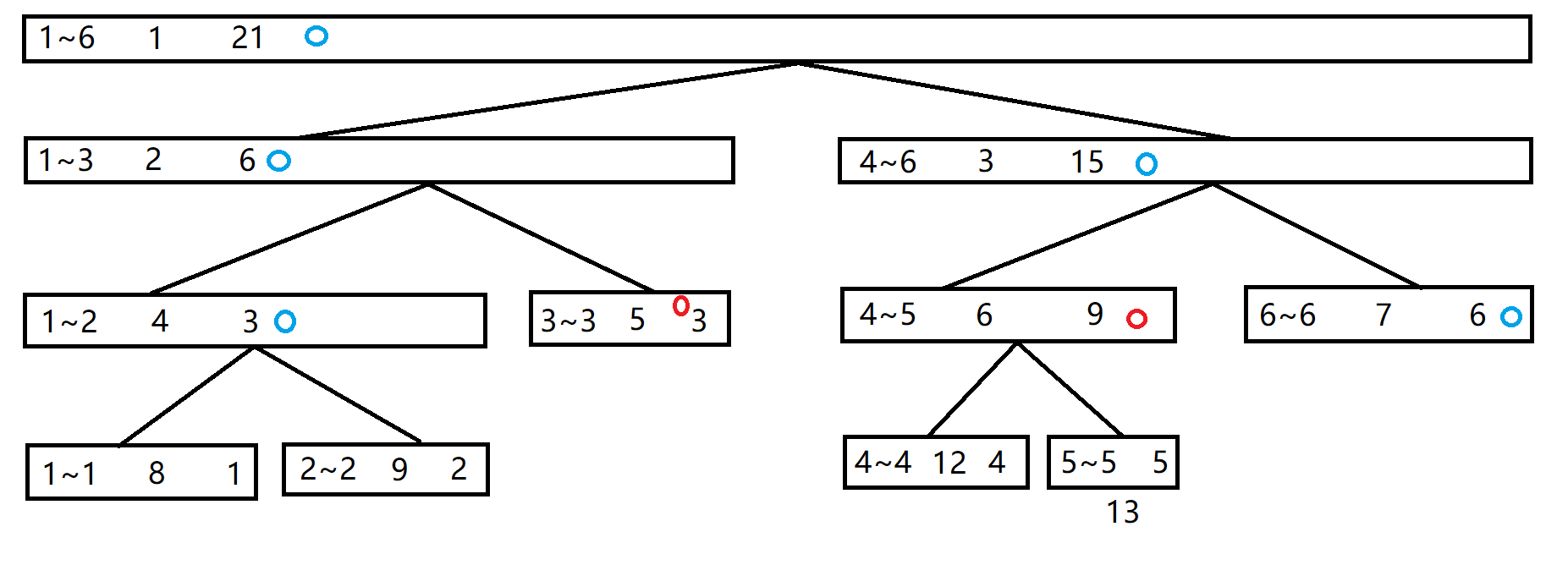
(图中标有蓝色的标记的点为在遍历过程中会遍历到的元素,标有红色标记的点为在区间 \([3,5]\) 的子区间。)
在每一次遍历中:
- 若这个区间被区间 \([3,5]\) 完全包含,则回溯此区间的元素值。
- 若这个区间和区间 \([3,5]\) 的交集不为空,则往下考虑往左右子树遍历。
- 若都不满足直接回溯。
现在考虑修改,我们很容易就可以想到一种 \(O(n\log_2n)\) 的修改操作,对于修改区间 \([l,r]\) 则让 \(l,l+1,\dots,r-1,r\) 这几个叶子节点区间加上对应值,然后回溯时 \(\text{push_up}\) 即可。
还有一种办法,我们先将每一个线段也就是线段树里的元素加一个属性——“懒标记”,再来看一下上一个图片:

每一个标有红色标记的点我们将他的给他加上当前值的懒标记,注意听然后就是最关键的一步。
我们再查询的过程中遇到有懒标记的点将他的懒标记下传,然后自己的懒标记清零,回溯的时候再 \(\text{push_up}\) 一遍就可以了。
修改加查询的代码如下:
void addtag(int u, int l, int r, LL k) { // 添加懒标记
ltag[u] += k, sum[u] += (r - l + 1) * k;
// 注意这里需要写成 += 否则就会将上一个懒标记清零,会挂。
}
void push_down(int u, int l, int r) { // 下传标记
if (ltag[u]) {
int mid = l + r >> 1;
addtag(u << 1, l, mid, ltag[u]);
addtag(u << 1 | 1, mid + 1, r, ltag[u]);
ltag[u] = 0;
}
}
void update(int L, int R, int u, int l, int r, LL k) { // 更新
if (L <= l && r <= R) {
addtag(u, l, r, k);
return;
}
push_down(u, l, r);
int mid = l + r >> 1;
if (L <= mid) {
update(L, R, u << 1, l, mid, k);
}
if (R > mid) {
update(L, R, u << 1 | 1, mid + 1, r, k);
}
push_up(u);
}
LL query(int L, int R, int u, int l, int r) { // 查询
if (L <= l & r <= R) {
return sum[u];
}
push_down(u, l, r);
int mid = l + r >> 1;
LL ret = 0;
if (L <= mid) {
ret += query(L, R, u << 1, l, mid);
}
if (R > mid) {
ret += query(L, R, u << 1 | 1, mid + 1, r);
}
return ret;
}