标签：right cdot times Pollard 算法 Rho mod left equiv

Pollard-Rho 分解算法

Pollard-Rho 算法是一种用于快速找到\(n\)的一个非平凡约数的方法。

生日悖论

在不少于\(23\)个人中至少有两人生日相同的概率已经大于\(50\%\)。

更一般的形式，随机选取在\(\left[ 1,N \right]\)范围内的整数，期望到第\(O(\sqrt{N})\)个出现重复。

用下面的方法可以简单估计一下。

\[\begin{aligned} &P\left( A \right) =1-\frac{n}{n}\times \frac{n-1}{n}\times \cdots\times \frac{n-k+1}{n}\ge \frac{1}{2} \\ &\Leftrightarrow\left( 1-\frac{1}{n} \right) \times \left( 1-\frac{2}{n} \right) \times \cdots\times \left( 1-\frac{k-1}{n} \right) \le \frac{1}{2} \\ &\text{根据不等式} 1+x\le e^x \\ &\Leftrightarrow\left( 1-\frac{1}{n} \right) \times \left( 1-\frac{2}{n} \right) \times \cdots\times \left( 1-\frac{k-1}{n} \right) \le e^{-\frac{k\cdot (k-1)}{2\cdot n}} \le \frac{1}{2} \\ &\Leftrightarrow k\ge \sqrt{2\cdot n\cdot \ln 2} \end{aligned} \]

Miller-Robin 素性测试

由于Pollard-Rho是用来寻找非平凡因子的，我们需要提前判断待分解数是否为素数。

费马小定理

若正整数\(a,p\)满足\(\left( a,p \right) =1\)，则有\(a^{p-1}\equiv 1 \left(\mod p\right)\)

• proof：
  显然\(\left\{ 0,1,2, \ldots ,p-1\right\}\)是\(p\)的一个完全剩余系。
  \(\left\{ 0\cdot a,1\cdot a,2\cdot a, \ldots ,(p-1)\cdot a\right\}\)也是\(p\)的一个完全剩余系。
  否则假设\(\exists i,j \subseteq \left\{ 0,1,2, \ldots ,p-1 \right\},i> j,i\cdot a\equiv j\cdot a (\mod p )\)那么\((i-j)\cdot a\equiv 0 (\mod p)\)而\(\left( a,p \right) =1\)所以\(i\equiv j (\mod p)\)出现矛盾。
  因此有$1\times 2\times \cdots \times (p-1)\equiv 1\cdot a\times 2\cdot a\times \cdots\times (p-1)\cdot a\equiv 1\times 2\times \cdots\times (p-1)\times a^{p-1}\left( \mod p \right) \Rightarrow a^{p-1}\equiv 1\left( \mod p \right) $

但遗憾的是，费马小定理的逆命题并不成立，例如$2^{340}\equiv 1\left( \mod 341 \right) $但\(341=11\times 31\)是个合数。

我们只能用费马小定理来判断一个数\(n\)是合数，若存在一个正整数\(a\)满足\(a^{n-1}\neq 1 \left( \mod n \right)\)则我们可以知道\(n\)一定是一个合数。这也是费马素性测试的内容，每次选取一个正整数\(a\)验证\(n\)的素性。

我们不总能通过增加参与测试的\(a\)的数量来提高正确率。因为存在一种数对$\forall b\subseteq \mathbb{N}^* ,(b,n)=1,b^{n-1}\equiv q\left( \mod n \right) $这种数被称为卡迈克尔数，例如\(561=3\cdot 11\cdot 17\)就是一个卡迈克尔数。\((b,561)=1\Rightarrow (b,3)=(b,11)=(b,17)=1\Rightarrow b^2\equiv 1\left( \mod 3 \right)\quad b^{10}\equiv 1\left( \mod 11 \right)\quad b^{16}\equiv 1\left( \mod 17 \right) \quad\Rightarrow\quad b^{560}\equiv (b^2)^{280}\equiv 1\left( \mod 3 \right) \quad b^{560}\equiv (b^10)^{56}\equiv 1\left( \mod 11 \right) \quad b^{560}\equiv (b^16)^{35}\equiv 1\left( \mod 17 \right) \quad \Rightarrow b^{560}\equiv 1\left( \mod 561 \right)\)

二次探测定理

若\(p\)是一个素数，则\(x^2\equiv 1\left( \mod p \right)\)的解只能是\(x\equiv1\left( \mod p \right) \quad x\equiv-1\left( \mod p \right)\)。

• proof:
  \(x^2\equiv1\left( \mod p \right)\Rightarrow (x+1)\cdot (x-1)\equiv 0 \left( \mod p \right) \Rightarrow p| (x+1)\cdot (x-1)\Rightarrow p|x+1 \quad || \quad p|x-1\)

米勒检验

我们可以在费马素性测试的基础上利用二次探测定理进行进一步测试，如果\(b^{n-1}\equiv 1(\mod n)\)且\(n\)为奇数，则检验\(b^{\frac{n-1}{2}}\equiv -1\)是否成立，若成立则认为\(n\)通过以\(b\)为基的米勒检验，若成立\(b^{\frac{n-1}{2}}\equiv 1\)则继续检验\(b^{\frac{n-1}{4}}\)。

令\(n\)是一个正整数，满足\(n>2,n-1=2^s\cdot t\)，其中\(s\)是一个非负整数，\(t\)是一个奇正整数。称\(n\)通过以\(b\)为基的米勒检验，如果有\(b^t\equiv 1(\mod n)\)或者\(b^{2^j\cdot t}\equiv -1(\mod n)\)对某个\(j\)成立，其中\(1\leq j\leq s-1\)。

数学家们已经证明，若\(n\)是一个奇正整数，那么最多有\(\frac{n-1}{4}\)个\(b\)，其中\(1\leq b \leq n-1\)，使得\(n\)能够通过以\(b\)为基的米勒检验。这说明如果随机选取\(k\)个正整数作为基，若\(n\)是一个合数，他通过所有\(k\)次米勒检验的概率仅为\(\left(\frac{1}{4}\right)^k\)。

可以验证，在\(2^{64}\)范围内，选取\(2,3,5,7,11,13,17,19,23,29, 31,37\)作为基，可以确定性的验证一个正整数是否为素数。

Pollard-Rho分解

根据生日悖论，我们随机的选取\(\left[ 1,N \right]\)之间的正整数，对于\(N\)的最小素因子\(p\)，大约在\(\sqrt{p}\)个数之后会出现两个数在模\(p\)意义下相等。

经验表明，在Pollard-Rho算法中选取，\(x_{k+1}\equiv x_k^2+c(\mod n)\)作为随机数生成器有非常好的表现。

下面的图可以直观的感受到Rho是什么意思

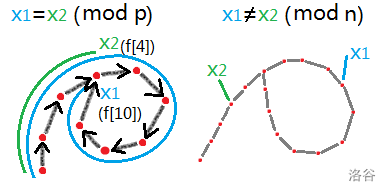
这说明如果\(x_i\equiv x_j(\mod p)\)则利用\(\operatorname{gcd}\left( \left\vert x_i-x_j \right\vert ,n \right)\)即可求出\(n\)的一个非平凡约数，如果不幸\(x_i=x_j\)那么会导致分解失败，然而事实上，由于\(p\leq\sqrt{n}\)模\(p\)的环远小于模\(n\)的环，分解失败的概率极小，失败之后只需要更换随机数生成器的种子再次尝试分解。

那么如何找到这个环呢，记录出现过的数，并在里面查找是不够优秀的，因为还要算上查找的时间复杂度。我们可以引入两个变量\(x,y\)，\(x\)每次走一步，\(y\)每次走两步，即\(x_{new}=x^2+c\quad y_{new}=(y^2+c)^2+c\)每次检验\(\operatorname{gcd}(\left\vert x-y \right\vert ,n)\)，经过环长步之后\(x,y\)总能相遇。

但是每次都求\(\operatorname{gcd}\)有点浪费时间，总的时间复杂度是\(O(n^{0.25}\cdot \log_2n)\)这边有一个小技巧就是把连续\(lim\)步的\(\left\vert x-y \right\vert\)相乘再做一次\(\operatorname{gcd}\)，取\(lim=O(\log_2n)\)就可以优化掉一个\(log\)。

另外Pollard-Rho往往在分解拥有大质因数的正整数时比较有效，在实际应用中可以先用试除法分解掉较小的质因子再用Pollard-Rho分解。

code：【模板】Pollard rho 算法

#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <ctime>
#include <iostream>
#define int long long

using namespace std;

const int d[12] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37};

int prime[200005], a[1000005], n, cnt = 0, div1[1005][2];

int gcd(int o, int p) { return (!p) ? o : gcd(p, o % p); }

int mi(__int128 o, int p, int mo) {
    __int128 yu = 1;
    while (p) {
        if (p & 1) yu = yu * o % mo;
        o = o * o % mo;
        p >>= 1;
    }
    return yu;
}

bool test(int o, int p) {
    int yu = p - 1;
    if (mi(o, yu, p) != 1) return 0;
    while (!(yu & 1)) {
        yu >>= 1;
        if (mi(o, yu, p) == (p - 1)) return 1;
    }
    return mi(o, yu, p) == 1;
}

bool Miller_Rabin(int o) {
    if (o <= 2) return 1;
    for (int i = 1; i < 12; i++)
        if (o == d[i]) return 1;
    for (int i = 0; i < 12; i++)
        if (!test(d[i], o)) return 0;
    return 1;
}

int Pollard_Rho(int n) {
    int x1 = 1ll * rand() * rand() * rand() * rand() % n + 1, y = x1,
        c = rand() + 1;
    for (int lim = 1;; lim = min(lim << 1, 128ll)) {
        int cnt = 1;
        for (int i = 1; i <= lim; i++) {
            x1 = (__int128)x1 * x1 % n + c;
            y = (__int128)y * y % n + c;
            y = (__int128)y * y % n + c;
            cnt = (__int128)cnt * (x1 - y) % n;
        }
        int yu = gcd(cnt, n);
        if (yu > 1) return yu;
    }
    return n;
}

signed main() {
    srand((unsigned)time(NULL));
    for (int i = 1; i <= 100000; i++) a[i] = 0;
    for (int i = 2; i <= 100000; i++) {
        if (!a[i]) prime[++cnt] = i;
        for (int j = 1; (j <= cnt) && (prime[j] * i <= 100000); j++) {
            a[prime[j] * i] = 1;
            if (i % prime[j] == 0) break;
        }
    }
    int T;
    cin >> T;
    while (T--) {
        int n, s0 = 0;
        scanf("%lld", &n);
        if (Miller_Rabin(n)) {
            printf("Prime\n");
            continue;
        }
        for (int i = 1; i <= cnt; i++) {
            if (n % prime[i] == 0) {
                s0++;
                div1[s0][0] = prime[i];
                div1[s0][1] = 0;
                while (n % prime[i] == 0) {
                    n /= prime[i];
                    div1[s0][1]++;
                }
            }
        }
        while (!Miller_Rabin(n)) {
            int yu = Pollard_Rho(n);
            n /= yu;
            if (yu > n) swap(n, yu);
            if (yu > 1) {
                div1[++s0][0] = yu;
                div1[s0][1] = 1;
                while (n % yu == 0) div1[s0][1]++, n /= yu;
            }
        }
        if (n > 1) div1[++s0][0] = n, div1[s0][1] = 1;
        int ans = 0;
        for (int i = 1; i <= s0; i++) ans = max(ans, div1[i][0]);
        printf("%lld\n", ans);
    }
    return 0;
}

标签：right,cdot,times,Pollard,算法,Rho,mod,left,equiv
From： https://www.cnblogs.com/clapp/p/17537670.html