原文:Hands-On Meta Learning with Python
译者:飞龙
本文来自【ApacheCN 深度学习 译文集】,采用译后编辑(MTPE)流程来尽可能提升效率。
不要担心自己的形象,只关心如何实现目标。——《原则》,生活原则 2.3.c
六、MAML 及其变体
在上一章中,我们了解了神经图灵机(NTM)以及它如何存储和从内存中检索信息。 我们还了解了称为记忆增强神经网络的 NTM 变体,该变体广泛用于单样本学习中。 在本章中,我们将学习一种有趣的,最流行的元学习算法,称为模型不可知元学习(MAML)。 我们将了解什么是不可知论元学习模型,以及如何在监督和强化学习设置中使用它。 我们还将学习如何从头开始构建 MAML,然后我们将学习对抗性元学习(ADML)。 我们将看到如何使用 ADML 查找健壮的模型参数。 接下来,我们将学习如何为分类任务实现 ADML。 最后,我们将学习用于元学习的上下文适应元学习(CAML)。
在本章中,您将了解以下内容:
- MAML
- MAML 算法
- 监督学习和强化学习设置中的 MAML
- 从头开始构建 MAML
- ADML
- 从头开始构建 ADML
- CAML
MAML
MAML 是最近推出且使用最广泛的元学习算法之一,它在元学习研究中创造了重大突破。 元学习是元学习的重点,我们知道,在元学习中,我们从仅包含少量数据点的各种相关任务中学习,并且元学习器会产生一个可以很好地概括新的相关任务的快速学习器,即使训练样本数量较少。
MAML 的基本思想是找到一个更好的初始参数,以便具有良好的初始参数,该模型可以以较少的梯度步骤快速学习新任务。
那么,那是什么意思呢? 假设我们正在使用神经网络执行分类任务。 我们如何训练网络? 我们将从初始化随机权重开始,并通过最小化损失来训练网络。 如何使损失最小化? 我们使用梯度下降。 好的,但是我们如何使用梯度下降来使损失最小化呢? 我们使用梯度下降法来找到最佳的权重,这将使我们损失最小。 我们采取多个梯度步骤来找到最佳权重,以便可以达到收敛。
在 MAML 中,我们尝试通过学习类似任务的分布来找到这些最佳权重。 因此,对于新任务,我们不必从随机初始化的权重开始,而是可以从最佳权重开始,这将花费较少的梯度步骤来达到收敛,并且不需要更多的数据点来进行训练。
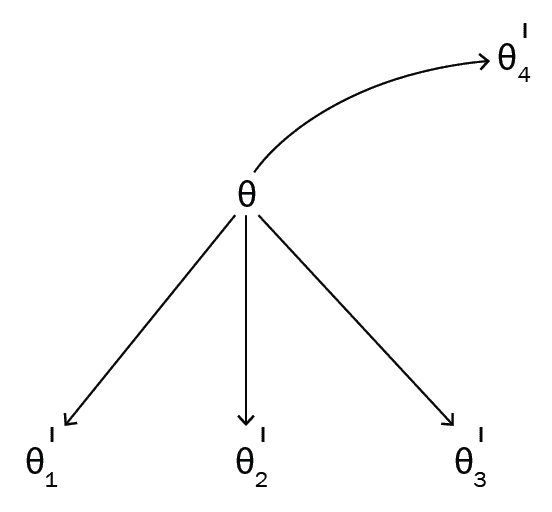
让我们简单地了解一下 MAML; 假设我们有三个相关任务: T1, T2, T3。 首先,我们随机初始化模型参数θ。 我们针对任务T1训练我们的网络。 然后,我们尝试通过梯度下降使损失L最小化。 通过找到最佳参数θ'[1],我们将损失降至最低。 同样,对于任务T2和T3,我们将以随机初始化的模型参数θ开始,并通过梯度下降找到正确的参数集来最小化损失。 假设θ'[2]和θ'[3]是任务的最佳参数,分别是T2和T3。
如下图所示,我们以随机初始化的参数θ开始每个任务,并通过为每个任务T查找最佳参数θ'[1],θ'[2]和θ'[3]来使损失最小化。 T1, T2, T3分别为:
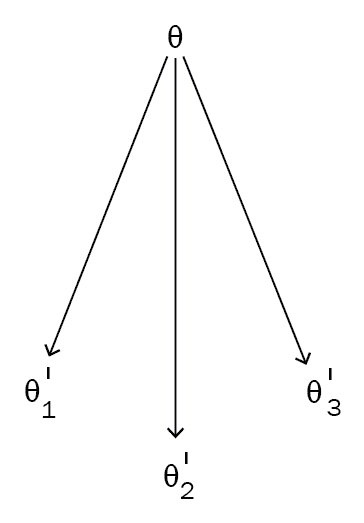
但是,如果不将θ初始化为随机位置(即使用随机值),则如果将θ初始化为所有三个任务都通用的位置,则无需采取更多的梯度步骤,也将花费更少的时间。 为了训练。 MAML 试图做到这一点。 MAML 试图找到许多相关任务共有的最佳参数θ,因此我们可以用较少的数据点相对较快地训练新任务,而不必执行许多梯度步骤。
如下图所示,我们将θ移至所有不同的最佳θ'值共有的位置:

因此,对于一个新的相关任务,例如T4,我们不必从随机初始化的参数θ开始。 相反,我们可以从最佳θ值开始,这样它将花费更少的梯度步骤来达到收敛。
因此,在 MAML 中,我们尝试找到相关任务共有的最佳θ值,以帮助我们从更少的数据点中学习并最大程度地减少训练时间。 MAML 与模型无关,这意味着我们可以将 MAML 应用于可通过梯度下降训练的任何模型。 但是 MAML 到底如何工作? 我们如何将模型参数移至最佳位置? 我们将在下一节中详细探讨。
MAML 算法
现在,我们对 MAML 有了基本的了解,我们将详细探讨它。 假设我们有一个由θ参数化的模型f,即f[θ](),我们在任务上有一个分布p(T)。 首先,我们用一些随机值初始化参数θ。 接下来,我们从任务分布中抽样一些任务Ti,即Ti ~ p(T)。 假设我们采样了五个任务, T = {T1, T2, ..., T5},然后,对于每个任务Ti,我们对k数据点进行采样并训练模型。 我们通过计算损失L[T[i]](f[θ])来做到这一点,并使用梯度下降来使损失最小化,并找到使损失最小的最佳参数集:

在前面的公式中,适用以下条件:
θ'[i]是任务Ti的最佳参数θ是初始参数α是超参数ᐁ[θ]L[T[i]]f(θ)是任务Ti的梯度
因此,在前面的梯度更新之后,我们将为采样的所有五个任务提供最佳参数:
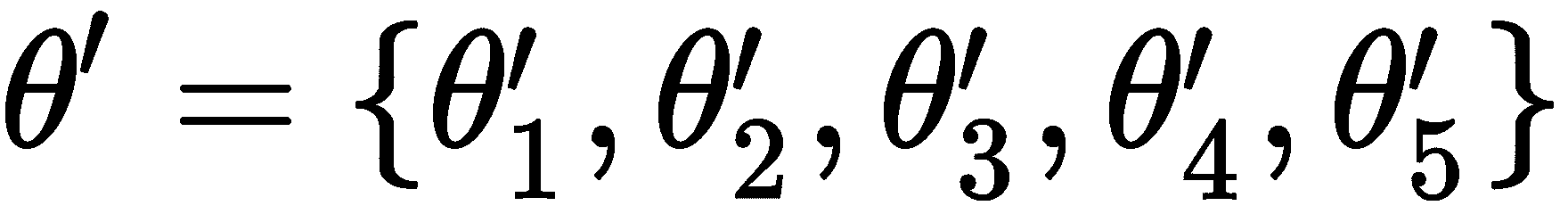
现在,在采样下一批任务之前,我们执行元更新或元优化。 也就是说,在上一步中,我们通过训练每个任务Ti找到了最佳参数θ'[i]。 现在,我们针对这些最佳参数θ'[i]计算梯度,并通过训练一组新任务Ti来更新随机初始化的参数θ。 这使我们随机初始化的参数θ移至最佳位置,在训练下一批任务时,我们无需采取许多梯度步骤。 此步骤称为元步骤,元更新,元优化或元训练。 可以表示为:

在前面的公式中,适用以下条件:
-
θ是我们的初始参数 -
β是超参数 -

是每个新任务
Ti相对于参数θ'[i]的梯度
如果您仔细看一下以前的元更新方程,我们会注意到我们正在更新模型参数θ,方法是仅取每个新任务Ti的参数θ'[i]最佳梯度平均值。
下图显示了 MAML 的总体算法; 我们的算法由两个循环组成:一个内部循环,我们在其中找到每个任务Ti的最佳参数θ'[i],一个外部循环,在其中我们通过计算相对于一组新任务Ti中最佳参数θ'[i]的梯度来确定θ,并更新随机初始化的模型参数:

我们应始终牢记,在更新外循环中的模型参数θ时,不应使用找到最佳参数θ'[i]的同一组任务Ti。
因此,简而言之,在 MAML 中,我们对一批任务进行了采样,对于批量中的每个任务Ti,我们使用梯度下降使损失最小化并获得最佳参数θ'[i]。 然后,在采样另一批任务之前,我们通过计算一组新任务Ti中最佳参数θ'[i]的梯度来更新随机初始化的模型参数θ。
监督学习中的 MAML
MAML 非常擅长寻找最佳初始参数,对吗? 现在,我们将看到如何在监督学习设置中使用 MAML。 在继续之前,让我们快速定义损失函数。 损失函数可以是根据我们正在执行的任务的任何函数。
如果执行回归,则可以将损失函数用作均方误差:

如果这是分类任务,那么我们可以使用损失函数,例如交叉熵损失:

现在,让我们一步一步地了解 MAML 如何在监督学习中使用:
-
假设我们有一个由参数θ参数化的模型
f,并且在任务p(T)上有分布。 首先,我们随机初始化模型参数θ。 -
我们从任务分布中抽取一些任务
Ti,即Ti ~ p(T)。 假设我们采样了三个任务,然后T = {T1, T2, T3}。 -
内循环:对于任务(
T)中的每个任务(Ti),我们对k个数据点进行采样,并准备我们的训练和测试数据集:
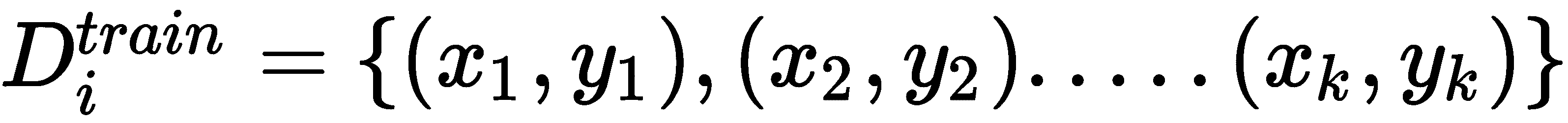

等待! 什么是训练集和测试集? 我们使用内循环中的训练集来找到最佳参数θ'[i],并使用外循环中的测试集来寻找最佳参数θ。 测试集并不意味着我们正在检查模型的表现。 它基本上充当外循环中的训练。 我们也可以将测试集称为元训练集。
现在,我们在D_train[i]上应用任何监督学习算法,使用梯度下降法计算损失并最小化损失,并获得最佳参数θ'[i],因此:

因此,对于每个任务,我们对k个数据点进行采样,并最小化训练集D_train[i]上的损失,并获得最佳参数θ'[i]。 当我们采样三个任务时,我们将拥有三个最佳参数θ'[i]。
- 外循环:我们在测试集(元训练集)中执行元优化-也就是说,在这里,我们尝试使测试集
D_test[i]中的损失最小化。 我们通过计算相对于上一步中计算出的最佳参数θ'[i]的梯度来最小化损失,并使用我们的测试集(元训练集)更新随机初始化的参数θ:
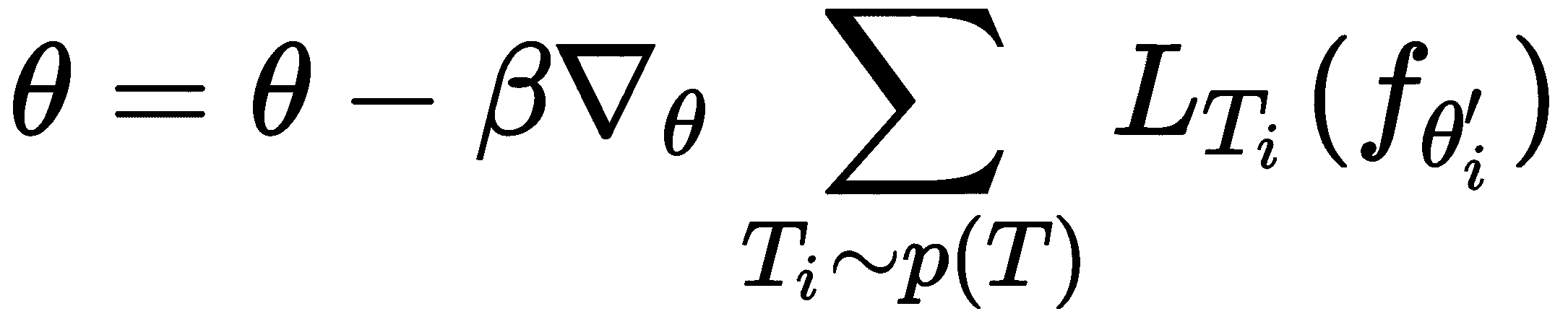
- 对于
n次迭代,我们重复步骤 2 到步骤 5。 下图为您提供了监督学习中的 MAML 概述:

从头开始构建 MAML
在上一节中,我们了解了 MAML 的工作原理。 我们看到了 MAML 如何获得更好,更健壮的模型参数θ,该参数可以在各个任务之间推广。 现在,我们将通过从头开始编码来更好地了解 MAML。 为了更好地理解,我们将考虑一个简单的二分类任务。 我们随机生成输入数据,并使用简单的单层神经网络对其进行训练,然后尝试找到最佳参数θ。 现在,我们将逐步逐步了解如何执行此操作:
您还可以在此处查看 Jupyter 笔记本中提供的代码,并附带说明。
首先,我们导入numpy库:
import numpy as np
生成数据点
现在,我们定义了一个称为sample_points的函数,用于生成我们的输入(x,y)对。 它以k参数作为输入,这意味着我们要采样的(x,y)对的数量:
def sample_points(k):
x = np.random.rand(k,50)
y = np.random.choice([0, 1], size=k, p=[.5, .5]).reshape([-1,1])
return x,y
前面的函数返回以下输出:
x, y = sample_points(10)
print x[0]
print y[0]
[0.537339 0.113621 0.62983308 0.3016117 0.91174146 0.95787598
0.20520229 0.123301 0.64143809 0.68485511 0.29509309 0.65719205
0.60906626 0.56890899 0.82614517 0.4408421 0.48018921 0.82674918
0.37076319 0.56239926 0.47655734 0.16489053 0.79742579 0.57731408
0.62065454 0.70110719 0.61330581 0.84084355 0.7967645 0.84148374
0.04915798 0.31650656 0.64326928 0.20878387 0.29682973 0.34488916
0.54626642 0.35608015 0.37950982 0.42281464 0.62984657 0.46538511
0.84092615 0.38056331 0.21669412 0.44118415 0.65537459 0.2136067
0.72679706 0.22969462]
[1]
单层神经网络
为了简单起见和更好地理解,我们使用只有一层的神经网络来预测输出:
a = np.matmul(X, theta)
YHat = sigmoid(a)
因此,我们使用 MAML 来找到可在各个任务之间推广的最佳参数值θ。 因此,对于一项新任务,我们可以通过采取较少的梯度步骤,在较短的时间内从几个数据点中学习。
将 MAML 用于训练
现在,我们定义一个名为MAML的类,在其中实现 MAML 算法。 在__init__方法中,我们将初始化所有必需的变量。 然后,我们定义我们的sigmoid激活函数。 在此之后,我们定义了train函数。
我们定义用于实现 MAML 的类:
class MAML(object):
我们定义__init__方法并初始化所有必需的变量:
def __init__(self):
我们初始化许多任务,即每批任务中需要的任务数:
self.num_tasks = 10
以下是每个任务中需要的样本数量(即镜头数量)和数据点数量[k):
self.num_samples = 10
以下是周期数,即训练迭代:
self.epochs = 1000
以下是内部循环(内部梯度更新)的超参数:
self.alpha = 0.0001
以下是外部循环(外部梯度更新)的超参数,即元优化:
self.beta = 0.0001
然后,我们随机初始化模型参数θ:
self.theta = np.random.normal(size=50).reshape(50, 1)
我们定义了sigmoid激活函数:
def sigmoid(self,a):
return 1.0 / (1 + np.exp(-a))
现在,让我们开始训练:
def train(self):
对于周期数:
for e in range(self.epochs):
self.theta_ = []
对于批量任务中的任务i:
for i in range(self.num_tasks):
对num_samples个数据点进行采样,并准备我们的训练集D_train[i]:
XTrain, YTrain = sample_points(self.num_samples)
我们通过单层神经网络预测YHat的值:
a = np.matmul(XTrain, self.theta)
YHat = self.sigmoid(a)
由于我们正在执行分类,因此我们将交叉熵损失用作损失函数:
loss = ((np.matmul(-YTrain.T, np.log(YHat)) - np.matmul((1 -YTrain.T), np.log(1 - YHat)))/self.num_samples)[0][0]
我们通过计算梯度将损失降至最低:
gradient = np.matmul(XTrain.T, (YHat - YTrain)) / self.num_samples
我们更新梯度并找到每个任务Ti的最佳参数θ',其中:

self.theta_.append(self.theta - self.alpha*gradient)
我们初始化元梯度:
meta_gradient = np.zeros(self.theta.shape)
然后,我们对k个数据点进行采样,并准备用于元训练的测试集(元训练集),即D_test[i]:
for i in range(self.num_tasks):
XTest, YTest = sample_points(10)
我们通过单层神经网络预测YPred的值:
a = np.matmul(XTest, self.theta_[i])
YPred = self.sigmoid(a)
我们计算元梯度:
meta_gradient += np.matmul(XTest.T, (YPred - YTest)) / self.num_samples
我们使用元梯度更新随机初始化的模型参数θ:

self.theta = self.theta-self.beta*meta_gradient/self.num_tasks
我们每隔 1000 个周期打印一次损失:
if e%1000==0:
print "Epoch {}: Loss {}\n".format(e,loss)
print 'Updated Model Parameter Theta\n'
print 'Sampling Next Batch of Tasks \n'
print '---------------------------------\n'
MAML类的完整代码如下:
class MAML(object):
def __init__(self):
#initialize number of tasks i.e number of tasks we need in each batch of tasks
self.num_tasks = 10
#number of samples i.e number of shots -number of data points (k) we need to have in each task
self.num_samples = 10
#number of epochs i.e training iterations
self.epochs = 10000
#hyperparameter for the inner loop (inner gradient update)
self.alpha = 0.0001
#hyperparameter for the outer loop (outer gradient update) i.e meta optimization
self.beta = 0.0001
#randomly initialize our model parameter theta
self.theta = np.random.normal(size=50).reshape(50, 1)
#define our sigmoid activation function
def sigmoid(self,a):
return 1.0 / (1 + np.exp(-a))
#now let's get to the interesting part i.e training
def train(self):
#for the number of epochs,
for e in range(self.epochs):
self.theta_ = []
#for task i in batch of tasks
for i in range(self.num_tasks):
#sample k data points and prepare our train set
XTrain, YTrain = sample_points(self.num_samples)
a = np.matmul(XTrain, self.theta)
YHat = self.sigmoid(a)
#since we are performing classification, we use cross entropy loss as our loss function
loss = ((np.matmul(-YTrain.T, np.log(YHat)) - np.matmul((1 -YTrain.T), np.log(1 - YHat)))/self.num_samples)[0][0]
#minimize the loss by calculating gradients
gradient = np.matmul(XTrain.T, (YHat - YTrain)) / self.num_samples
#update the gradients and find the optimal parameter theta' for each of tasks
self.theta_.append(self.theta - self.alpha*gradient)
#initialize meta gradients
meta_gradient = np.zeros(self.theta.shape)
for i in range(self.num_tasks):
#sample k data points and prepare our test set for meta training
XTest, YTest = sample_points(10)
#predict the value of y
a = np.matmul(XTest, self.theta_[i])
YPred = self.sigmoid(a)
#compute meta gradients
meta_gradient += np.matmul(XTest.T, (YPred - YTest)) / self.num_samples
#update our randomly initialized model parameter theta with the meta gradients
self.theta = self.theta-self.beta*meta_gradient/self.num_tasks
if e%1000==0:
print "Epoch {}: Loss {}\n".format(e,loss)
print 'Updated Model Parameter Theta\n'
print 'Sampling Next Batch of Tasks \n'
print '---------------------------------\n'
现在,让我们为MAML类创建一个实例:
model = MAML()
我们开始训练模型:
model.train()
我们可以看到如下输出: 我们可以注意到,损失从周期 0 的 2.71 急剧减少到周期 3,000 的 0.5:
Epoch 0: Loss 2.71883405043
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 1000: Loss 1.7829716017
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 2000: Loss 1.29532754055
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 3000: Loss 0.599713728648
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
MAML 强化学习
如何在强化学习(RL)设置中应用 MAML? 在 RL 中,我们的目标是找到正确的策略函数,该函数将告诉我们在每种状态下要执行哪些操作。 但是我们如何在 RL 中应用元学习呢? 假设我们训练了智能体以解决两臂老丨虎丨机问题。 但是,我们不能使用相同的智能体来解决四臂老丨虎丨机问题。 我们必须再次从头开始训练智能体,以解决这个新的四臂老丨虎丨机问题。 当另一名n臂老丨虎丨机进来时,情况也是如此。我们一直在从头训练智能体以解决新问题,即使它与智能体已经学会解决的问题密切相关。 因此,代替执行此操作,我们可以应用元学习并在一组相关任务上对智能体进行训练,以便智能体可以利用其先前的知识在最短的时间内学习新的相关任务,而无需从头开始进行训练。
在 RL 中,我们可以将轨迹称为包含一系列观察和动作的元组。 因此,我们在这些轨迹上训练模型以学习最佳策略。 但是,同样,我们应该使用哪种算法来训练我们的模型? 对于 MAML,我们可以使用可以通过梯度下降训练的任何 RL 算法。 我们使用策略梯度来训练我们的模型。 策略梯度通过直接将带有某些参数θ的策略π参数化为π[θ]来找到最佳策略。 因此,使用 MAML,我们尝试找到可在各个任务之间推广的最佳参数θ。
但是我们的损失函数应该是什么? 在 RL 中,我们的目标是通过最大化正向奖励和最小化负向奖励来找到最优策略,因此我们的损失函数变为最小化负向奖励,它可以表示为:

但是上一个方程式中发生了什么? R(x[y, t])表示时间t的状态x和动作a的奖励,t = 1至H表示我们的时间步长,其中H是地平线-我们的最终时间步长。
假设我们有一个由θ参数化的模型f,也就是f[θ]()和任务的分布p(T)。 首先,我们用一些随机值初始化参数θ。 接下来,我们从任务分布中抽样一些任务Ti: Ti ~ p(T)。
然后,对于每个任务,我们对k轨迹进行采样,并构建训练和测试集:D_train[i], D_test[i] ~ T[i]。 我们的数据集基本上包含诸如观察和动作之类的轨迹信息。 通过执行梯度下降,我们将训练集D_train[i]上的损失降至最低,并找到最佳参数θ':

现在,在采样下一批任务之前,我们执行元更新-也就是说,我们尝试通过计算相对于最佳参数θ'[i]的损失梯度来最大程度地减少测试集D_test[i]上的损失,并更新随机初始化的参数θ:

对抗式元学习
我们已经看到了如何使用 MAML 查找可跨任务通用的最佳参数θ。 现在,我们将看到一个称为 ADML 的 MAML 变体,该变体同时使用干净样本和对抗样本来查找更好且更健壮的初始模型参数θ。 在继续之前,让我们了解什么是对抗性样本。 通过对抗攻击获得对抗样本。 假设我们有一张图片; 对抗性攻击包括以无法被我们的眼睛察觉的方式稍微修改此图像,并将此修改后的图像称为对抗图像。 当我们将该对抗图像提供给模型时,它无法正确分类。 有几种不同的对抗攻击可用于获取对抗样本。 我们将看到一种常用的方法,称为快速梯度符号方法(FGSM)。
FGSM
假设我们正在执行图像分类; 通常,我们通过计算损失并通过相对于模型参数(例如权重)计算损失的梯度并更新模型参数来尝试使损失最小化来训练模型。 为了获得图像的对抗样本,我们计算损失相对于图像输入像素的梯度,而不是模型参数。 因此,图像的对抗样本基本上是相对于图像的损失梯度。 我们只采取一个梯度步骤,因此它在计算上是有效的。 计算完梯度后,我们取其符号。
对抗图像可以如下计算:

在前面的公式中,适用以下条件:
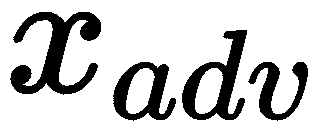 是对抗图片
是对抗图片 是输入图像
是输入图像 是相对于我们输入图像的损失梯度
是相对于我们输入图像的损失梯度
如您在下图中所看到的,我们有一个输入图像x,并且通过将损失相对于我们的图像的梯度符号添加到实际图像中,我们得到了对抗图像。
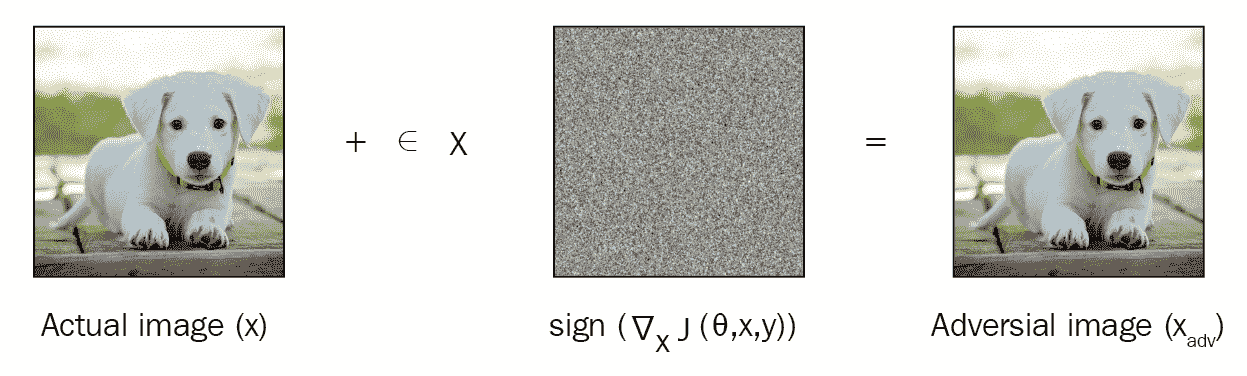
ADML
现在,我们已经了解了什么是对抗性样本以及如何生成对抗性样本,我们将看到如何在元学习中使用这些对抗性样本。 我们使用干净样本和对抗样本训练元学习模型。 但是,需要使用对抗样本训练模型吗? 它有助于我们找到鲁棒的模型参数θ。 干净样本和对抗样本均在算法的内部和外部循环中使用,并且同样有助于更新模型参数。 ADML 使用干净样本和对抗样本之间的这种变化的相关性来获得更好,更健壮的模型参数初始化,从而使我们的参数对对抗样本变得健壮,并且可以很好地推广到新任务。
因此,当我们有任务分布p(T),时,我们从任务分布中采样了一批任务Ti,对于每个任务,我们采样k个数据点,并准备我们的训练和测试集。
在 ADML 中,我们将训练集和测试集的干净样本和对抗样本采样为D_train[clean_i],D_train[adv_i],D_test[clean_i],D_test[adv_i]。
现在,我们在训练上计算损失,通过梯度下降使损失最小,并找到最佳参数θ'。 由于我们拥有干净的和对抗的训练集,因此我们对这两个集合都执行梯度下降,并分别为干净的和对抗集找到最佳参数θ'[i]和θ'[adv_i]:


现在,我们进入元训练阶段,通过计算损失相对于上一步获得的最佳参数θ'的梯度,通过使测试集上的损失最小来找到最佳参数θ。
因此,我们通过计算相对于最佳参数θ'[i]和θ'[adv_i]的损失梯度,通过最小化纯净D_test[clean_i]和对抗性D_test[adv_i]测试集的损失来更新模型参数θ:
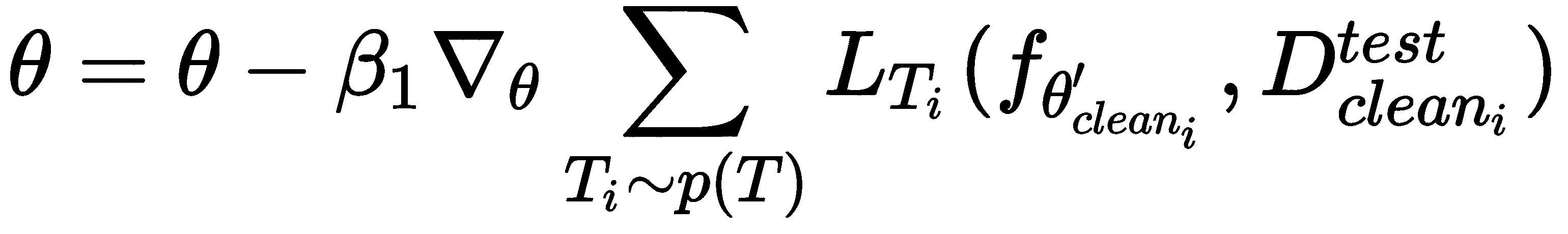
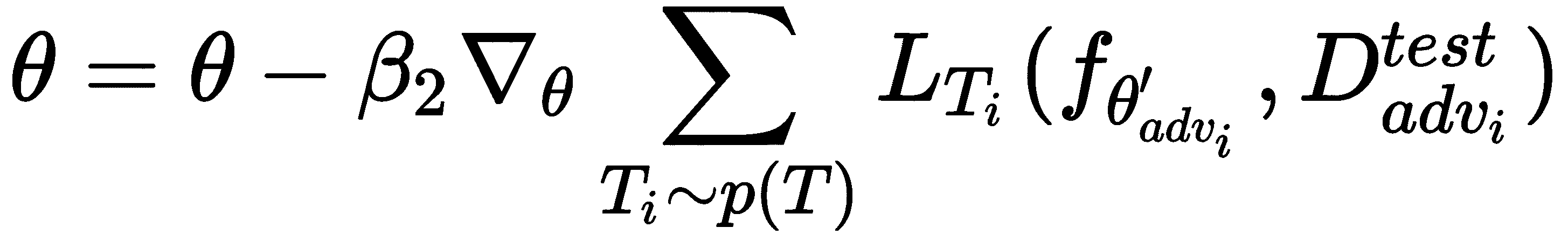
从头开始构建 ADML
在上一节中,我们了解了 ADML 的工作原理。 我们看到了如何使用干净样本和对抗样本训练我们的模型,以获得更好,更健壮的模型参数θ,该参数可在各个任务之间推广。 现在,我们将通过从头开始编码来更好地理解 ADML。 为了更好地理解,我们将考虑一个简单的二分类任务。 我们随机生成输入数据,并使用单层神经网络对其进行训练,然后尝试找到最佳参数theta。 现在,我们将逐步了解 ADML 的工作原理。
您还可以在此处查看 Jupyter 笔记本中提供的代码,并附带说明。
首先,我们导入所有必需的库:
import tensorflow as tf
import numpy as np
生成数据点
现在,我们定义了一个称为sample_points的函数,用于生成纯净输入(x和y)对。 它以k参数作为输入,这意味着我们要采样许多(x,y)对:
def sample_points(k):
x = np.random.rand(k,50)
y = np.random.choice([0, 1], size=k, p=[.5, .5]).reshape([-1,1])
return x,y
前面的函数返回以下输出:
x, y = sample_points(10)
print x[0]
print y[0]
[0.69922136 0.77305793 0.72227583 0.45291578 0.52828294 0.65308614
0.77281836 0.59878078 0.71554901 0.51660327 0.65538137 0.25267594
0.13763862 0.12522582 0.16336571 0.87987815 0.64465771 0.86281232
0.24503599 0.85324859 0.62247917 0.58166159 0.47871545 0.75025566
0.87919612 0.49545388 0.31058753 0.66306459 0.34621453 0.56970739
0.84310111 0.08747573 0.48944231 0.50061581 0.86215915 0.3248433
0.01350084 0.23846395 0.91015074 0.04968178 0.59098773 0.74692099
0.92763503 0.16319537 0.69655162 0.20419323 0.58241944 0.15703596
0.76047838 0.93452557]
[0]
FGSM
现在,我们定义了另一个称为FGSM的函数,用于生成对抗性输入。 我们使用 FGSM 生成对抗性样本。 我们已经看到了 FGSM 如何通过计算相对于输入而不是模型参数的梯度来生成对抗对。 因此,我们将干净(x,y)对作为输入,并生成对抗(x_adv,y)对:
def FGSM(x,y):
#placeholder for the inputs x and y
X = tf.placeholder(tf.float32)
Y = tf.placeholder(tf.float32)
#initialize theta with random values
theta = tf.Variable(tf.zeros([50,1]))
#predict the value of y
YHat = tf.nn.softmax(tf.matmul(X, theta))
#calculate the loss
loss = tf.reduce_mean(-tf.reduce_sum(Y*tf.log(YHat), reduction_indices=1))
#now calculate gradient of our loss function with respect to our input X instead of model parameter theta
gradient = ((tf.gradients(loss,X)[0]))
#calculate the adversarial input
#i.e x_adv = x + epsilon * sign ( nabla_x J(X, Y))
X_adv = X + 0.2*tf.sign(gradient)
X_adv = tf.clip_by_value(X_adv,-1.0,1.0)
#start the tensoflow session
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
X_adv = sess.run(X_adv, feed_dict={X: x, Y: y})
return X_adv, y
单层神经网络
我们使用具有单层的神经网络来预测输出:
a = np.matmul(X, theta)
YHat = sigmoid(a)
因此,我们使用 ADML 查找可在各个任务之间推广的最佳参数值θ。 因此,对于一项新任务,我们可以通过采取较少的梯度步骤,在较短的时间内从几个数据点中学习。
对抗式元学习
现在,我们定义一个名为ADML的类,在其中实现 ADML 算法。 在__init__方法中,我们将初始化所有必需的变量。 然后,我们定义sigmoid函数,并定义train函数。
我们将逐步介绍此步骤,稍后再看完整的最终代码:
class ADML(object):
我们定义__init__方法并初始化必要的变量:
def __init__(self):
我们初始化许多任务,即每批任务中需要的任务数:
self.num_tasks = 2
我们初始化每个任务中需要的多个样本(即多个镜头)和多个数据点(k):
self.num_samples = 10
我们初始化多个周期,即训练迭代:
self.epochs = 100
内循环(内部梯度更新)的超参数如下:
#for clean sample
self.alpha1 = 0.0001
#for adversarial sample
self.alpha2 = 0.0001
外循环(外梯度更新)的超参数(是元优化)如下:
#for clean sample
self.beta1 = 0.0001
#for adversarial sample
self.beta2 = 0.0001
我们随机初始化模型参数theta:
self.theta = np.random.normal(size=50).reshape(50, 1)
我们定义了sigmoid激活函数:
def sigmoid(self,a):
return 1.0 / (1 + np.exp(-a))
现在,让我们看看如何训练网络:
def train(self):
对于周期数:
for e in range(self.epochs):
#theta' of clean samples
self.theta_clean = []
#theta' of adversarial samples
self.theta_adv = []
对于批量任务中的任务i:
for i in range(self.num_tasks):
我们对k个数据点进行采样,并准备我们的训练数据。 首先,我们采样干净的数据点,即D_train[clean_i]:
XTrain_clean, YTrain_clean = sample_points(self.num_samples)
将干净的样本送入 FGSM 并获得对抗性样本D_train[adv_i]:
XTrain_adv, YTrain_adv = FGSM(XTrain_clean,YTrain_clean)
现在,我们计算θ'[clean_i]并将其存储在theta_clean中。 使用单层网络预测输出:
a = np.matmul(XTrain_clean, self.theta)
YHat = self.sigmoid(a)
由于我们正在执行分类,因此我们将交叉熵损失用作损失函数:
loss = ((np.matmul(-YTrain_clean.T, np.log(YHat)) - np.matmul((1 -YTrain_clean.T), np.log(1 - YHat)))/self.num_samples)[0][0]
我们通过计算梯度将损失降至最低:
gradient = np.matmul(XTrain_clean.T, (YHat - YTrain_clean)) / self.num_samples
我们更新梯度并找到干净样本的最佳参数θ'[i]:

self.theta_clean.append(self.theta - self.alpha1*gradient)
现在,我们计算对抗样本的θ'[adv_i]并将其存储在theta_adv中:
#predict the output y
a = (np.matmul(XTrain_adv, self.theta))
YHat = self.sigmoid(a)
#calculate cross entropy loss
loss = ((np.matmul(-YTrain_adv.T, np.log(YHat)) - np.matmul((1 -YTrain_adv.T), np.log(1 - YHat)))/self.num_samples)[0][0]
#minimize the loss by calculating gradients
gradient = np.matmul(XTrain_adv.T, (YHat - YTrain_adv)) / self.num_samples
我们更新梯度并找到对抗样本的最佳参数θ'[i],
 :
:
self.theta_adv.append(self.theta - self.alpha2*gradient)
我们为干净样本和对抗样本初始化元梯度:
meta_gradient_clean = np.zeros(self.theta.shape)
#initialize meta gradients for adversarial samples
meta_gradient_adv = np.zeros(self.theta.shape)
对于i个任务:
for i in range(self.num_tasks):
我们对k个数据点进行了采样,并准备了干净的和对抗的测试集(元训练集)进行元训练-即D_test[clean_i]和D_test[adv_i]:
#first, we sample clean data points
XTest_clean, YTest_clean = sample_points(self.num_samples)
#feed the clean samples to FGSM and get adversarial samples
XTest_adv, YTest_adv = sample_points(self.num_samples)
首先,我们计算干净样本的元梯度:
#predict the value of y
a = np.matmul(XTest_clean, self.theta_clean[i])
YPred = self.sigmoid(a)
#compute meta gradients
meta_gradient_clean += np.matmul(XTest_clean.T, (YPred - YTest_clean)) / self.num_samples
现在,我们计算对抗样本的元梯度:
#predict the value of y
a = (np.matmul(XTest_adv, self.theta_adv[i]))
YPred = self.sigmoid(a)
#compute meta gradients
meta_gradient_adv += np.matmul(XTest_adv.T, (YPred - YTest_adv)) / self.num_samples
我们使用干净样本和对抗样本的元梯度更新随机初始化的模型参数θ:


self.theta = self.theta-self.beta1*meta_gradient_clean/self.num_tasks
self.theta = self.theta-self.beta2*meta_gradient_adv/self.num_tasks
我们每 10 个周期打印一次损失:
if e%10==0:
print "Epoch {}: Loss {}\n".format(e,loss)
print 'Updated Model Parameter Theta\n'
print 'Sampling Next Batch of Tasks \n'
print '---------------------------------\n'
ADML类的完整代码如下:
class ADML(object):
def __init__(self):
#initialize number of tasks i.e number of tasks we need in each batch of tasks
self.num_tasks = 2
#number of samples i.e number of shots -number of data points (k) we need to have in each task
self.num_samples = 10
#number of epochs i.e training iterations
self.epochs = 100
#hyperparameter for the inner loop (inner gradient update)
#for clean sample
self.alpha1 = 0.0001
#for adversarial sample
self.alpha2 = 0.0001
#hyperparameter for the outer loop (outer gradient update) i.e meta optimization
#for clean sample
self.beta1 = 0.0001
#for adversarial sample
self.beta2 = 0.0001
#randomly initialize our model parameter theta
self.theta = np.random.normal(size=50).reshape(50, 1)
#define our sigmoid activation function
def sigmoid(self,a):
return 1.0 / (1 + np.exp(-a))
#now let's get to the interesting part i.e training
def train(self):
#for the number of epochs,
for e in range(self.epochs):
#theta' of clean samples
self.theta_clean = []
#theta' of adversarial samples
self.theta_adv = []
#for task i in batch of tasks
for i in range(self.num_tasks):
#sample k data points and prepare our training data
#first, we sample clean data points
XTrain_clean, YTrain_clean = sample_points(self.num_samples)
#feed the clean samples to FGSM and get adversarial samples
XTrain_adv, YTrain_adv = FGSM(XTrain_clean,YTrain_clean)
#1\. First, we computer theta' for clean samples and store it in theta_clean
#predict the output y
a = np.matmul(XTrain_clean, self.theta)
YHat = self.sigmoid(a)
#since we are performing classification, we use cross entropy loss as our loss function
loss = ((np.matmul(-YTrain_clean.T, np.log(YHat)) - np.matmul((1 -YTrain_clean.T), np.log(1 - YHat)))/self.num_samples)[0][0]
#minimize the loss by calculating gradients
gradient = np.matmul(XTrain_clean.T, (YHat - YTrain_clean)) / self.num_samples
#update the gradients and find the optimal parameter theta' for clean samples
self.theta_clean.append(self.theta - self.alpha1*gradient)
#2\. Now, we compute theta' for adversarial samples and store it in theta_clean
#predict the output y
a = (np.matmul(XTrain_adv, self.theta))
YHat = self.sigmoid(a)
#calculate cross entropy loss
loss = ((np.matmul(-YTrain_adv.T, np.log(YHat)) - np.matmul((1 -YTrain_adv.T), np.log(1 - YHat)))/self.num_samples)[0][0]
#minimize the loss by calculating gradients
gradient = np.matmul(XTrain_adv.T, (YHat - YTrain_adv)) / self.num_samples
#update the gradients and find the optimal parameter theta' for adversarial samples
self.theta_adv.append(self.theta - self.alpha2*gradient)
#initialize meta gradients for clean samples
meta_gradient_clean = np.zeros(self.theta.shape)
#initialize meta gradients for adversarial samples
meta_gradient_adv = np.zeros(self.theta.shape)
for i in range(self.num_tasks):
#sample k data points and prepare our test set for meta training
#first, we sample clean data points
XTest_clean, YTest_clean = sample_points(self.num_samples)
#feed the clean samples to FGSM and get adversarial samples
XTest_adv, YTest_adv = sample_points(self.num_samples)
#1\. First, we computer meta gradients for clean samples
#predict the value of y
a = np.matmul(XTest_clean, self.theta_clean[i])
YPred = self.sigmoid(a)
#compute meta gradients
meta_gradient_clean += np.matmul(XTest_clean.T, (YPred - YTest_clean)) / self.num_samples
#2\. Now, we compute meta gradients for adversarial samples
#predict the value of y
a = (np.matmul(XTest_adv, self.theta_adv[i]))
YPred = self.sigmoid(a)
#compute meta gradients
meta_gradient_adv += np.matmul(XTest_adv.T, (YPred - YTest_adv)) / self.num_samples
#update our randomly initialized model parameter theta
#with the meta gradients of both clean and adversarial samples
self.theta = self.theta-self.beta1*meta_gradient_clean/self.num_tasks
self.theta = self.theta-self.beta2*meta_gradient_adv/self.num_tasks
if e%10==0:
print "Epoch {}: Loss {}\n".format(e,loss)
print 'Updated Model Parameter Theta\n'
print 'Sampling Next Batch of Tasks \n'
print '---------------------------------\n'
我们为ADML类创建一个实例:
model = ADML()
然后,我们开始训练模型:
model.train()
您会注意到损失如何随着时间的推移而减少:
Epoch 0: Loss 100.25943711532
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 10: Loss 2.13533264312
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 20: Loss 0.426824910313
Updated Model Parameter Theta
Sampling Next Batch of Tasks
CAML
我们已经看到了 MAML 如何找到模型的最佳初始参数,从而可以轻松地以较少的梯度步骤将其适应于新任务。 现在,我们将看到一个有趣的 MAML 变体,称为 CAML。 CAML 的概念非常简单,与 MAML 相同。 它还尝试找到更好的初始参数。 我们了解了 MAML 如何使用两个循环。 在内部循环中,MAML 学习特定于任务的参数,并尝试使用梯度下降来最大程度地减少损失,在外部循环中,它更新模型参数以减少跨多个任务的预期损失,以便我们可以使用更新的模型参数作为相关任务的更好的初始化。
在 CAML 中,我们对 MAML 算法进行了非常小的调整。 在这里,我们不使用单个模型参数,而是将模型参数分成两个部分:
- 上下文参数:它是在内部循环上更新的特定于任务的参数。 用 denoted 表示,它特定于每个任务,代表单个任务的嵌入。
- 共享参数:跨任务共享,并在外循环中更新以找到最佳模型参数。 用
θ表示。
因此,上下文参数在内部循环中针对每个任务进行调整,并且共享参数在各个任务之间共享,并用于外部循环中的元训练。 在每个适应步骤之前,我们将上下文参数初始化为零。
好的; 但是在将我们的参数分为两个不同的参数时真正有用的是什么? 它用于避免针对特定任务的过拟合,促进更快的学习,并且具有高效的内存。
CAML 算法
现在,让我们逐步了解 CAML 的工作原理:
-
假设我们有一个由参数θ参数化的模型
f,并且在任务p(T)上有分布。 首先,我们随机初始化模型参数θ。 我们还初始化了上下文参数∅[0] = 0。 -
现在,我们从任务分布中抽样一些任务
Ti,即Ti ~ p(T)。 -
内循环:对于任务(
T)中的每个任务(Ti),我们采样k个数据点并准备我们的训练和测试数据集:
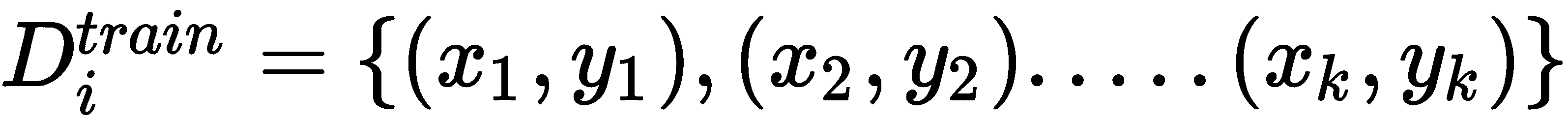
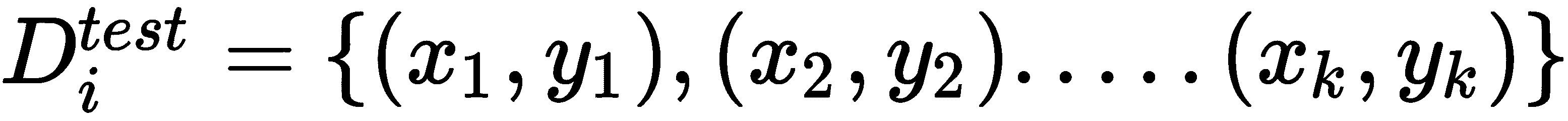
现在,我们将上下文参数设置为0:
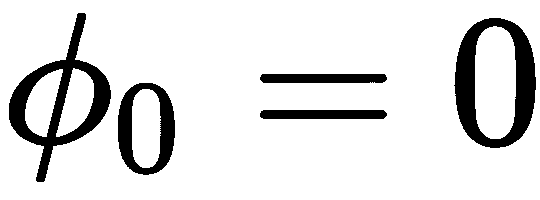
然后,我们计算D_train[i]的损失,使用梯度下降法将损失最小化,并学习任务特定参数∅[i]:

- 外循环:现在,我们在测试集中执行元优化-也就是说,在这里,我们尝试使测试集中
D_test[i]中的损失最小化并找到最佳参数:
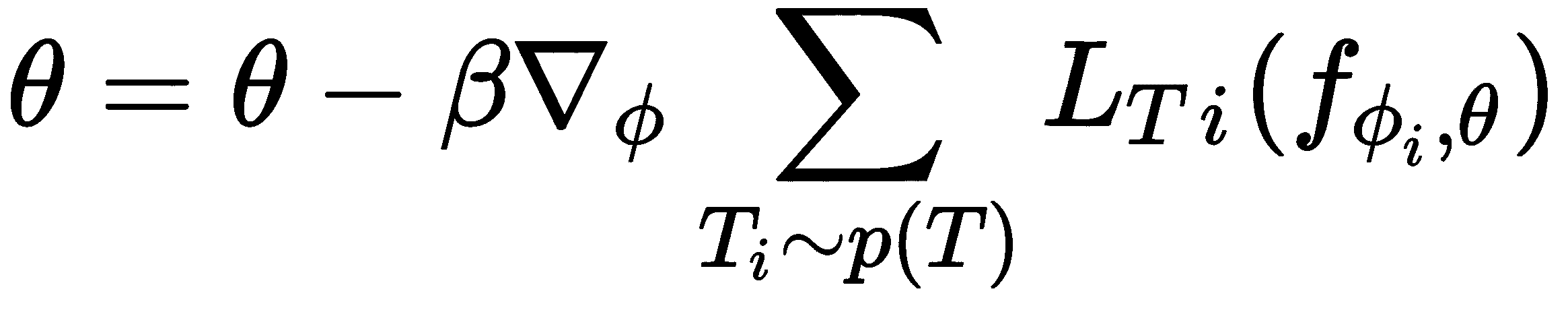
- 对
n次迭代重复步骤 2 到步骤 4。
总结
在本章中,我们学习了如何找到可在各个任务之间推广的最佳模型参数θ,以便我们可以减少梯度步骤,并快速学习新的相关任务。 我们从 MAML 开始,我们看到了 MAML 如何执行元优化来计算最佳模型参数。 接下来,我们看到了对抗性元学习,其中我们使用了干净样本和对抗性样本来查找可靠的初始模型参数。 后来,我们了解了 CAML,并看到了 CAML 如何使用两个不同的参数,一个用于在任务中学习,另一个用于更新模型参数。
在下一章中,我们将学习元 SGD 和 Reptile 算法,该算法再次用于查找模型的更好的初始参数。
问题
- 什么是 MAML?
- 为什么 MAML 模型不可知?
- 什么是对抗性元学习?
- 什么是 FGSM?
- 什么是上下文参数?
- 什么是共享参数?
进一步阅读
七、元 SGD 和 Reptile
在上一章中,我们学习了如何使用 MAML 查找可在多个任务中推广的最佳参数。 我们看到了 MAML 如何通过计算元梯度和执行元优化来计算此最佳参数。 我们还看到了对抗性元学习,它通过添加对抗性样本并使 MAML 在干净样本和对抗性样本之间进行搏斗以找到最佳参数,从而增强了 MAML。 我们还看到了 CAML,或者说是元学习的上下文适应。 在本章中,我们将学习元 SGD,这是另一种用于快速执行学习的元学习算法。 与 MAML 不同,元 SGD 不仅会找到最佳参数,还将找到最佳学习率和更新方向。 我们将看到如何在监督学习和强化学习设置中使用元 SGD。 我们还将看到如何从头开始构建元 SGD。 继续,我们将学习 Reptile 算法,该算法对 MAML 进行了改进。 我们将看到 Reptile 与 MAML 有何不同,然后将介绍如何在正弦波回归任务中使用 Reptile。
在本章中,您将了解以下内容:
- 元 SGD
- 监督学习中的元 SGD
- 强化学习中的元 SGD
- 从头开始构建元 SGD
- Reptile
- 将 Reptile 用于正弦波回归
元 SGD
假设我们有一些任务T。 我们使用通过某些参数θ参数化的模型f,并训练模型以最大程度地减少损失。 我们使用梯度下降使损失最小化,并找到模型的最佳参数θ'[i]。
让我们回想一下梯度下降的更新规则:
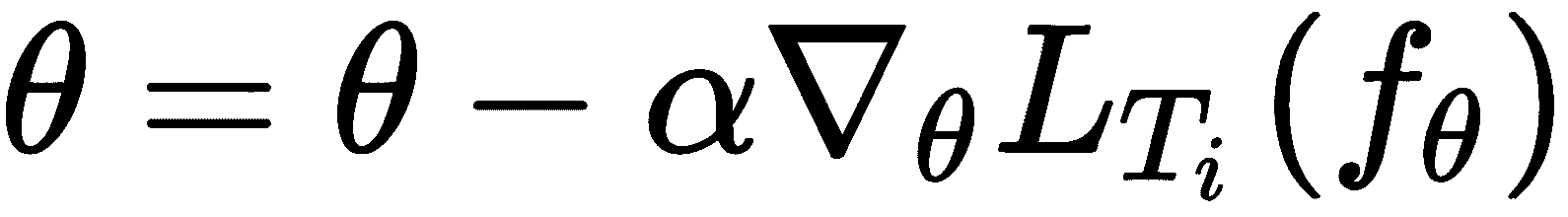
那么,构成梯度下降的关键因素是什么? 让我们来看看:
- 参数
θ - 学习率
α - 更新方向
我们通常将参数θ设置为某个随机值,并在训练过程中尝试找到最佳值,然后将学习率α的值设置为一个小数值,或者将其随时间衰减,以及跟随梯度的更新方向。 我们是否可以通过元学习来学习梯度下降的所有这些关键特征,以便可以从几个数据点快速学习? 在上一章中,我们已经看到 MAML 如何找到可在各个任务之间推广的最佳初始参数θ。 有了最佳的初始参数,我们就可以减少梯度步骤,并快速学习新任务。
因此,现在我们是否可以学习最佳的学习率和更新方向,从而可以跨任务进行概括,从而实现更快的收敛和训练? 让我们看看如何通过将其与 MAML 进行比较在元 SGD 中学习。 如果您还记得,请在 MAML 内循环中,通过最小化梯度下降带来的损失,找到每个任务T[i]的最佳参数θ'[i]:
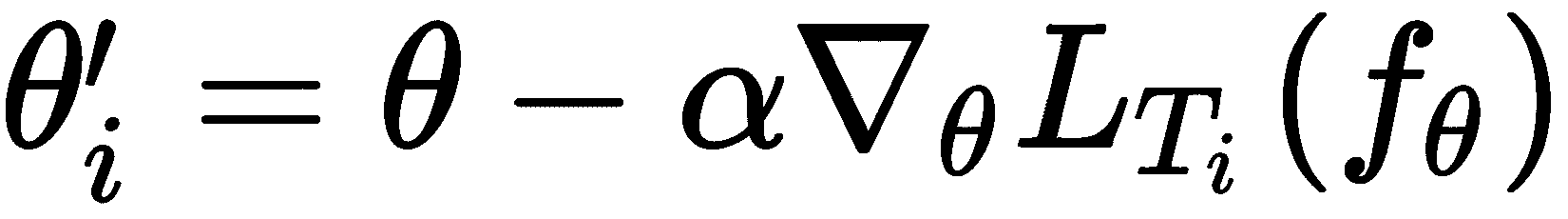
对于元 SGD,我们可以按如下方式重写前面的公式:

但是有什么区别呢? 此处α不仅是一个标量小值,而且是一个向量。 我们以与θ相同的形状随机初始化α。我们将θ称为初始参数,将αᐁ[θ]L[T[i]](f[θ])称为自适应项。 因此,自适应项表示更新方向,其长度成为学习率。 我们在自适应项的方向而不是在梯度方向ᐁ[θ]L[T[i]](f[θ])上更新我们的值,并且在自适应项中隐式地实现了我们的学习率。
因此,在元 SGD 中,我们不会使用较小的标量值来初始化学习率α。 相反,我们使用与θ相同形状的随机值来初始化学习率,并与θ一起学习它们。 我们采样了一些任务,并且对于每个任务,我们采样了一些k数据点,并使用梯度下降使损失最小化,但是我们的更新方程式变为:

也就是说,我们的更新方向是自适应项方向,而不是梯度方向,并且我们将α与θ一起学习。
现在,在外循环中,我们执行元优化-也就是说,我们计算相对于最佳参数θ'[i]的损失梯度,并更新我们随机初始化的模型参数θ。 在元 SGD 中,我们还更新了随机初始化的α,而不是单独更新θ,如下所示:

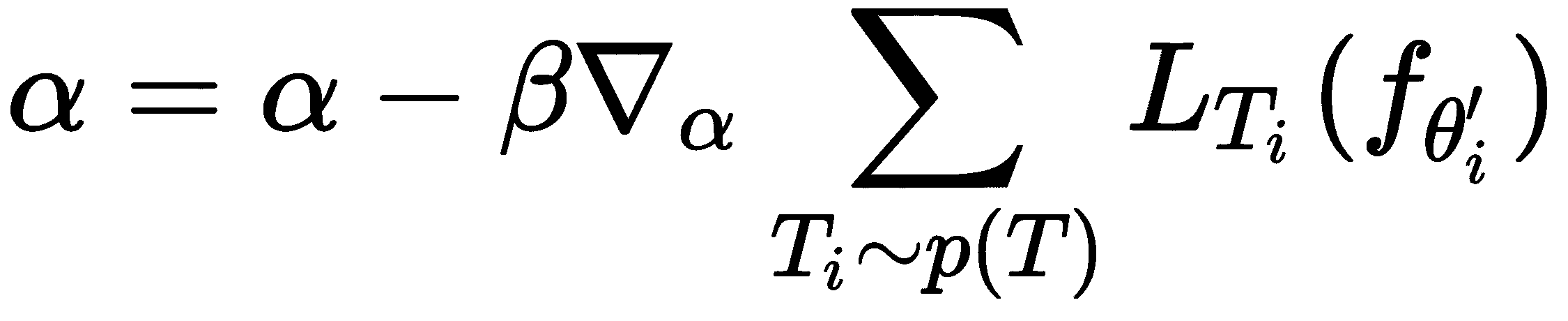
如您所见,元 SGD 只是对 MAML 的一小部分调整。 在 MAML 中,我们随机初始化模型参数θ,并尝试找到可跨任务通用的最佳参数。 在元 SGD 中,我们不仅学习模型参数θ,还学习了学习率和更新方向,这在适应性项中隐含地实现。
用于监督学习的元 SGD
现在,我们将看到如何在有监督的学习环境中使用元 SGD。 与 MAML 一样,我们可以将元 SGD 应用于可以通过梯度下降训练的任何监督学习问题,无论是回归学习还是分类学习。 首先,我们需要定义我们要使用的损失函数。 例如,如果要执行分类,则可以使用交叉熵作为损失函数,如果要进行回归,则可以使用均方误差作为损失函数。 我们可以使用适合我们任务的任何损失函数。 让我们逐步进行以下操作:
-
假设我们有一个由参数
θ参数化的模型f,并且在任务!p(T)上有一个分布。 首先,我们随机初始化模型参数θ,并随机初始化α形状与θ相同的形状。 -
我们从任务分布中抽样一些任务
T[i]:T[i] ~ p(T)。 假设我们已经采样了三个任务,然后是T = {T[1]m T[2], T[3]}。 -
内循环:对于任务(
T)中的每个任务(T[i]),我们对k数据点进行采样,并准备训练和测试数据集:


现在,我们在D_train[i]上应用了一种监督学习算法,使用梯度下降法计算并最小化了损失,并获得了最佳参数θ'[i]:
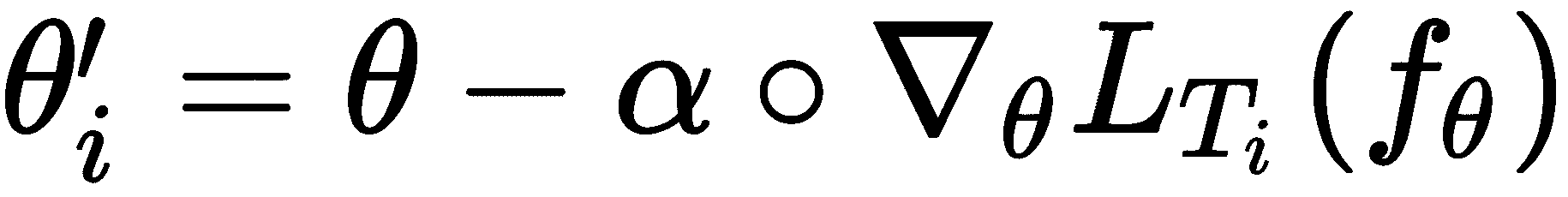
因此,对于每个任务,我们对k个数据点进行采样,并最大程度地减少训练集D_train[i]上的损失,并获得最佳参数θ'[i]。 当我们采样三个任务时,我们将拥有三个最佳参数θ'[i]。
- 外循环:现在,我们在测试集(元训练集)中执行元优化-也就是说,在这里,我们尝试使测试集
D_test[i]中的损失最小化。 通过计算相对于上一步中计算出的最佳参数θ'[i]的梯度,我们将损失降至最低,并使用测试集更新随机初始化的参数θ。 我们不仅更新θ,还更新我们的随机初始化参数α,它可以表示为:
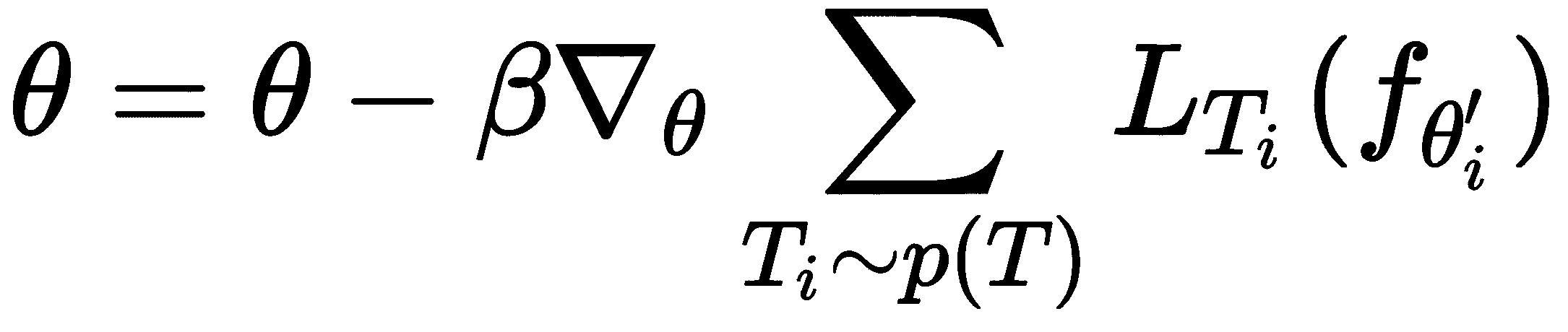
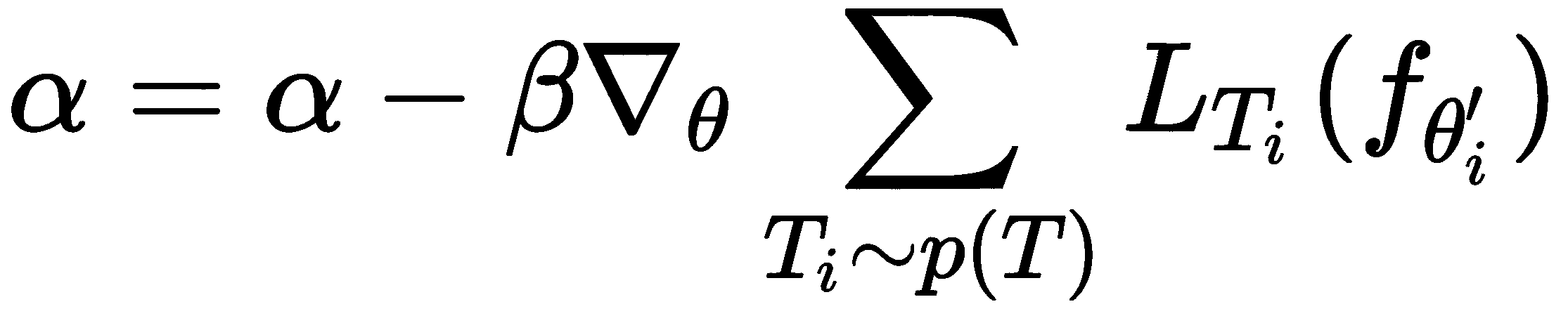
- 对于
n次迭代,我们重复步骤 2 到步骤 4。
从头开始构建元 SGD
在上一节中,我们了解了元 SGD 的工作原理。 我们看到了元 SGD 如何获得更好,更健壮的模型参数θ,该参数可跨任务进行通用化,并具有最佳的学习率和更新方向。 现在,我们将从头开始对元 SGD 进行编码,以更好地了解它们。 就像我们在 MAML 中所做的一样,为了更好地理解,我们将考虑一个简单的二分类任务。 我们随机生成输入数据,并使用简单的单层神经网络对其进行训练,并尝试找到最佳参数θ'[i]。 我们将逐步详细介绍如何执行此操作。
您还可以在此处查看 Jupyter 笔记本中提供的代码,并提供说明。
首先,我们导入numpy库:
import numpy as np
生成数据点
现在,我们定义了一个名为sample_points的函数,用于生成输入(x, y)对。 它以参数k作为输入,这意味着我们要采样的(x, y)对的数量:
def sample_points(k):
x = np.random.rand(k,50)
y = np.random.choice([0, 1], size=k, p=[.5, .5]).reshape([-1,1])
return x,y
前面的函数返回的输出如下:
x, y = sample_points(10)
print x[0]
print y[0]
[5.01913307e-01 1.01874941e-01 7.16678998e-01 3.90294047e-01
2.95330904e-01 8.66751993e-01 5.09988127e-01 8.59389493e-01
5.16202142e-01 7.92016358e-01 8.24237307e-01 7.76739141e-01
8.57034917e-01 2.75862141e-01 6.44874856e-01 2.75248940e-01
5.67665047e-01 9.61564994e-01 7.58931873e-01 1.08989614e-02
7.69325529e-01 4.05955016e-01 1.98799935e-01 9.94134622e-01
3.07179216e-01 1.34756367e-01 2.92326855e-01 5.00026528e-01
7.23673231e-01 5.28698231e-01 1.52495715e-01 9.20139339e-01
1.76127500e-02 2.42244262e-01 7.09515862e-01 7.10358091e-01
6.47656449e-01 5.15623266e-01 8.77002211e-01 4.18744855e-01
9.67902538e-01 8.79261670e-01 5.88524781e-01 5.11397703e-02
7.07513737e-01 4.61998029e-01 8.77306226e-01 5.32049083e-01
8.07178697e-01 5.01521846e-04]
[1]
单层神经网络
我们使用只有一层的神经网络来预测输出:
a = np.matmul(X, theta)
YHat = sigmoid(a)
因此,我们使用元 SGD 查找最佳参数值theta,学习率和梯度更新方向,这些方向可在各个任务之间推广。 因此,对于一项新任务,我们可以通过采取较少的梯度步骤,在较短的时间内从几个数据点中学习。
元 SGD
现在,我们定义一个名为MetaSGD的类,在其中实现元 SGD 算法。 在__init__方法中,我们将初始化所有必需的变量。 然后,我们定义 Sigmoid 激活函数。 之后,我们定义训练函数:
class MetaSGD(object):
我们定义__init__方法并初始化所有必需的变量:
def __init__(self):
#initialize number of tasks i.e number of tasks we need in each batch of tasks
self.num_tasks = 2
#number of samples i.e number of shots -number of data points (k) we need to have in each task
self.num_samples = 10
#number of epochs i.e training iterations
self.epochs = 10000
#hyperparameter for the outer loop (outer gradient update) i.e meta optimization
self.beta = 0.0001
#randomly initialize our model parameter theta
self.theta = np.random.normal(size=50).reshape(50, 1)
#randomly initialize alpha with same shape as theta
self.alpha = np.random.normal(size=50).reshape(50, 1)
我们定义了sigmoid激活函数:
def sigmoid(self,a):
return 1.0 / (1 + np.exp(-a))
现在,让我们开始训练:
def train(self):
对于周期数:
for e in range(self.epochs):
self.theta_ = []
对于一批任务中的i任务:
for i in range(self.num_tasks):
我们对k个数据点进行采样,并准备训练集:
XTrain, YTrain = sample_points(self.num_samples)
然后,我们使用单层网络预测y的值:
a = np.matmul(XTrain, self.theta)
YHat = self.sigmoid(a)
我们计算损失并计算梯度:
#since we're performing classification, we use cross entropy loss as our loss function
loss = ((np.matmul(-YTrain.T, np.log(YHat)) - np.matmul((1 -YTrain.T), np.log(1 - YHat)))/self.num_samples)[0][0]
#minimize the loss by calculating gradients
gradient = np.matmul(XTrain.T, (YHat - YTrain)) / self.num_samples
之后,我们更新梯度并为每个任务找到最佳参数θ'[i]:
self.theta_.append(self.theta - (np.multiply(self.alpha,gradient)))
我们初始化元梯度:
meta_gradient = np.zeros(self.theta.shape)
for i in range(self.num_tasks):
我们对k个数据点进行采样,并准备用于元训练D_test[i]的测试集:
XTest, YTest = sample_points(10)
然后,我们预测y的值:
a = np.matmul(XTest, self.theta_[i])
YPred = self.sigmoid(a)
我们计算元梯度:
meta_gradient += np.matmul(XTest.T, (YPred - YTest)) / self.num_samples
现在,我们更新模型参数theta和alpha:

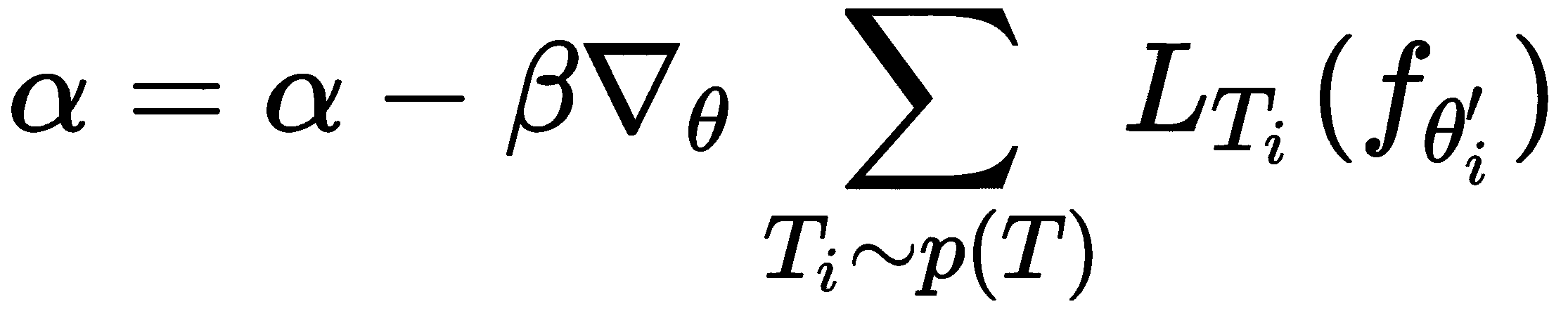
self.theta = self.theta-self.beta*meta_gradient/self.num_tasks
self.alpha = self.alpha-self.beta*meta_gradient/self.num_tasks
我们每 1000 个周期打印一次损失:
if e%1000==0:
print "Epoch {}: Loss {}\n".format(e,loss)
print 'Updated Model Parameter Theta\n'
print 'Sampling Next Batch of Tasks \n'
print '---------------------------------\n'
MetaSGD的完整代码如下:
class MetaSGD(object):
def __init__(self):
#initialize number of tasks i.e number of tasks we need in each batch of tasks
self.num_tasks = 2
#number of samples i.e number of shots -number of data points (k) we need to have in each task
self.num_samples = 10
#number of epochs i.e training iterations
self.epochs = 10000
#hyperparameter for the inner loop (inner gradient update)
self.alpha = 0.0001
#hyperparameter for the outer loop (outer gradient update) i.e meta optimization
self.beta = 0.0001
#randomly initialize our model parameter theta
self.theta = np.random.normal(size=50).reshape(50, 1)
#randomly initialize alpha with same shape as theta
self.alpha = np.random.normal(size=50).reshape(50, 1)
#define our sigmoid activation function
def sigmoid(self,a):
return 1.0 / (1 + np.exp(-a))
#now let's get to the interesting part i.e training :P
def train(self):
#for the number of epochs,
for e in range(self.epochs):
self.theta_ = []
#for task i in batch of tasks
for i in range(self.num_tasks):
#sample k data points and prepare our train set
XTrain, YTrain = sample_points(self.num_samples)
a = np.matmul(XTrain, self.theta)
YHat = self.sigmoid(a)
#since we're performing classification, we use cross entropy loss as our loss function
loss = ((np.matmul(-YTrain.T, np.log(YHat)) - np.matmul((1 -YTrain.T), np.log(1 - YHat)))/self.num_samples)[0][0]
#minimize the loss by calculating gradients
gradient = np.matmul(XTrain.T, (YHat - YTrain)) / self.num_samples
#update the gradients and find the optimal parameter theta' for each of tasks
self.theta_.append(self.theta - (np.multiply(self.alpha,gradient)))
#initialize meta gradients
meta_gradient = np.zeros(self.theta.shape)
for i in range(self.num_tasks):
#sample k data points and prepare our test set for meta training
XTest, YTest = sample_points(10)
#predict the value of y
a = np.matmul(XTest, self.theta_[i])
YPred = self.sigmoid(a)
#compute meta gradients
meta_gradient += np.matmul(XTest.T, (YPred - YTest)) / self.num_samples
#update our randomly initialized model parameter theta with the meta gradients
self.theta = self.theta-self.beta*meta_gradient/self.num_tasks
#update our randomly initialized hyperparameter alpha with the meta gradients
self.alpha = self.alpha-self.beta*meta_gradient/self.num_tasks
if e%1000==0:
print "Epoch {}: Loss {}\n".format(e,loss)
print 'Updated Model Parameter Theta\n'
print 'Sampling Next Batch of Tasks \n'
print '---------------------------------\n'
我们创建MetaSGD类的实例:
model = MetaSGD()
让我们开始训练模型:
model.train()
您可以通过各种周期看到损失如何最小化:
Epoch 0: Loss 2.22523195333
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 1000: Loss 1.951785305709
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 2000: Loss 1.47382270343
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 3000: Loss 1.07296354822
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
元 SGD 用于强化学习
现在,我们将了解如何在强化学习中使用元 SGD。元 SGD 与可以通过梯度下降训练的任何 RL 算法兼容。
- 假设我们有一个由参数
θ参数化的模型f,并且在任务p(T)上有一个分布。 首先,我们随机初始化模型参数θ,并随机初始化形状与θ相同的α。 - 从任务分布中采样一些任务
T[i]:T[i] ~ p(T)。 假设我们已经采样了三个任务T = {T[1], T[2], T[3]}。 - 内循环:对于任务(
T)中的每个任务(T[i]),我们对D_train[i]轨迹进行采样,使用梯度下降计算损失并将损失最小化,并获得最佳参数θ'[i]。因此,对于每个任务,我们都对轨迹进行采样,最大程度地减少损失并获得最佳参数θ'[i]。 当我们采样三个任务时,对于所有三个任务,我们将拥有三个最佳参数θ'[i]。 接下来,我们将对另一组称为D_test[i]的轨迹进行元更新。 - 外循环:现在,我们在
D_test[i]轨迹中执行元优化。 我们通过计算相对于上一步获得的最佳参数θ'[i]的梯度,更新我们随机初始化的参数θ和α来使损失最小化:


- 对于
n次迭代,我们重复步骤 2 到步骤 4。
Reptile
Reptile 算法已被 OpenAI 提出作为对 MAML 的改进。 它很容易实现。 我们知道,在 MAML 中,我们可以计算二阶导数,即梯度的梯度。 但是从计算上来说,这不是一个有效的任务。 因此,OpenAI 提出了对 MAML 的改进,称为 Reptile。 Reptile 的算法非常简单。 对一些n个任务进行采样,然后运行随机梯度下降(SGD),以减少每个采样任务的迭代次数,然后沿某个方向更新模型参数,这是所有任务的共同点。 由于我们对每个任务执行的 SGD 迭代次数较少,因此间接暗示我们正在计算损失的二阶导数。 与 MAML 不同,它在计算上很有效,因为我们不直接计算二阶导数也不展开计算图,因此易于实现。
假设我们从任务分布中采样了两个任务T[1]和T[2],并随机初始化了模型参数θ。 首先,我们接受任务T[1]并对某些n次迭代执行 SGD,并获得最佳参数θ'[i]。 然后我们执行下一个任务T[2],迭代执行 SGD n次,并获得最佳参数θ'[i]。 因此,我们有两个最佳参数集:θ' = {θ'[1], θ'[2]}。 现在,我们需要沿更靠近这两个最佳参数的方向移动参数θ,如下图所示:

但是,如何在更接近最佳参数θ'[i]的方向上移动随机初始化的模型参数θ呢? 首先,我们需要找到随机初始化的模型参数θ与最佳参数集θ'之间的距离。 因此,我们使用欧几里得距离D作为找到该距离的距离度量。 找到θ和θ'之间的距离后,我们需要将它们最小化:

最小化θ和θ'之间的距离实际上会将我们随机初始化的模型参数θ移向更接近最佳参数θ'[i]的方向。 但是我们如何才能最小化这个距离呢? 我们基本上计算距离ᐁ[θ]E[1/2 D(θ, θ')^2]的梯度以将其最小化,它可以编写如下:

因此,在计算了梯度之后,我们的最终更新方程变为:
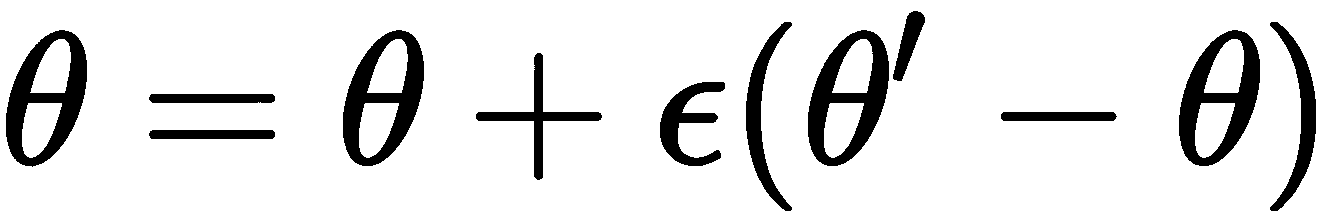
通过使用先前的方程式更新模型参数θ,我们实质上使初始参数θ与最佳参数值θ'之间的距离最小。 因此,我们通过执行n次迭代的 SGD,找到每个任务的最佳参数。 一旦获得了最佳参数集,就可以使用先前的公式更新模型参数θ。
Reptile 算法
Reptile 是一种简单而有效的算法。 Reptile 可以实现串行和批量版本。 在串行版本中,我们仅从任务分发中抽样一个任务,而在批量版本中,我们对一批任务进行抽样并尝试找到最佳参数。 我们将看到 Reptile 的串行版本如何工作。 Reptile 所涉及的步骤顺序如下:
- 假设我们有任务的分布
p(T),并且我们随机初始化模型参数θ。 - 现在我们从任务分布
T ~ p(T)中抽取任务T。 - 对于采样的任务
T,我们对k个数据点进行采样,并准备我们的数据集D:D = {(x1, y1), (x2, y2), 。.., (xk, yk)}。 我们的数据集基本上包含x特征和y标签。 现在,我们通过对某些n迭代次数执行随机梯度下降来最大程度地减少数据集中的损失。 在对采样任务T,执行n次迭代的 SGD 之后,我们将获得最佳参数θ'[i]。 - 我们在更接近先前步骤中获得的最佳参数
θ'[i]的方向上更新了随机初始化的参数θ如下:θ = θ + ε(θ - θ')。 - 对于
n迭代次数,我们重复步骤 2 到步骤 4。
将 Reptile 用于正弦波回归
在上一节中,我们了解了 Reptile 的工作原理。 现在,我们将从头开始对 Reptile 进行编码,从而更好地理解它。 假设我们有一个任务集合,每个任务的目标是在给定一些输入的情况下使正弦波的输出回归。 那是什么意思呢?
假设y = amplitude * sin(x + phase)。 我们算法的目标是学习在给定x的情况下对y的值进行回归。 幅度的值在 0.1 到 5.0 之间随机选择,相位的值在 0 到π之间随机选择。 因此,对于每个任务,我们仅采样 10 个数据点并训练网络-也就是说,对于每个任务,我们仅采样 10 个(x, y)对。 让我们看一下代码并详细查看它。
您还可以在此处查看 Jupyter 笔记本中提供的代码,并提供说明。
首先,我们导入所有必需的库:
import tensorflow as tf
import numpy as np
生成数据点
现在,我们定义了一个称为sample_points的函数,用于生成(x, y)对。 它以参数k作为输入,这意味着我们要采样的(x, y)对的数量:
def sample_points(k):
num_points = 100
#amplitude
amplitude = np.random.uniform(low=0.1, high=5.0)
#phase
phase = np.random.uniform(low=0, high=np.pi)
x = np.linspace(-5, 5, num_points)
#y = a*sin(x+b)
y = amplitude * np.sin(x + phase)
#sample k data points
sample = np.random.choice(np.arange(num_points), size=k)
return (x[sample], y[sample])
两层神经网络
像 MAML 一样,Reptile 也与可以通过梯度下降训练的任何算法兼容。 因此,我们使用具有 64 个隐藏单元的简单两层神经网络。
首先,让我们重置 TensorFlow 图:
tf.reset_default_graph()
我们初始化网络参数:
num_hidden = 64
num_classes = 1
num_feature = 1
接下来,我们为输入和输出定义占位符:
X = tf.placeholder(tf.float32, shape=[None, num_feature])
Y = tf.placeholder(tf.float32, shape=[None, num_classes])
我们随机初始化模型参数:
w1 = tf.Variable(tf.random_uniform([num_feature, num_hidden]))
b1 = tf.Variable(tf.random_uniform([num_hidden]))
w2 = tf.Variable(tf.random_uniform([num_hidden, num_classes]))
b2 = tf.Variable(tf.random_uniform([num_classes]))
然后,我们执行前馈操作以预测输出Yhat:
#layer 1
z1 = tf.matmul(X, w1) + b1
a1 = tf.nn.tanh(z1)
#output layer
z2 = tf.matmul(a1, w2) + b2
Yhat = tf.nn.tanh(z2)
我们使用均方误差作为损失函数:
loss_function = tf.reduce_mean(tf.square(Yhat - Y))
然后,我们使用 Adam 优化器将损失降至最低:
optimizer = tf.train.AdamOptimizer(1e-2).minimize(loss_function)
我们初始化 TensorFlow 变量:
init = tf.global_variables_initializer()
Reptile
现在,我们将看到如何使用 Reptile 找到神经网络的最佳参数。
首先,我们初始化必要的变量:
#number of epochs i.e training iterations
num_epochs = 100
#number of samples i.e number of shots
num_samples = 50
#number of tasks
num_tasks = 2
#number of times we want to perform optimization
num_iterations = 10
#mini btach size
mini_batch = 10
然后,我们开始 TensorFlow 会话:
with tf.Session() as sess:
sess.run(init)
对于周期数:
for e in range(num_epochs):
#for each task in batch of tasks
for task in range(num_tasks):
我们得到模型的初始参数:
old_w1, old_b1, old_w2, old_b2 = sess.run([w1, b1, w2, b2,])
然后,我们对x和y进行采样:
x_sample, y_sample = sample_points(num_samples)
对于某些k迭代,我们对任务执行优化:
for k in range(num_iterations):
#get the minibatch x and y
for i in range(0, num_samples, mini_batch):
#sample mini batch of examples
x_minibatch = x_sample[i:i+mini_batch]
y_minibatch = y_sample[i:i+mini_batch]
train = sess.run(optimizer, feed_dict={X: x_minibatch.reshape(mini_batch,1),
Y: y_minibatch.reshape(mini_batch,1)})
经过几次优化迭代后,我们获得了更新的模型参数:
new_w1, new_b1, new_w2, new_b2 = sess.run([w1, b1, w2, b2])
现在,我们执行元更新:
epsilon = 0.1
updated_w1 = old_w1 + epsilon * (new_w1 - old_w1)
updated_b1 = old_b1 + epsilon * (new_b1 - old_b1)
updated_w2 = old_w2 + epsilon * (new_w2 - old_w2)
updated_b2 = old_b2 + epsilon * (new_b2 - old_b2)
我们使用新参数更新模型参数:
w1.load(updated_w1, sess)
b1.load(updated_b1, sess)
w2.load(updated_w2, sess)
b2.load(updated_b2, sess)
然后,我们每 10 个周期打印一次损失:
if e%10 == 0:
loss = sess.run(loss_function, feed_dict={X: x_sample.reshape(num_samples,1), Y: y_sample.reshape(num_samples,1)})
print "Epoch {}: Loss {}\n".format(e,loss)
print 'Updated Model Parameter Theta\n'
print 'Sampling Next Batch of Tasks \n'
print '---------------------------------\n'
完整的代码如下:
#start the tensorflow session
with tf.Session() as sess:
sess.run(init)
for e in range(num_epochs):
#for each task in batch of tasks
for task in range(num_tasks):
#get the initial parameters of the model
old_w1, old_b1, old_w2, old_b2 = sess.run([w1, b1, w2, b2,])
#sample x and y
x_sample, y_sample = sample_points(num_samples)
#for some k number of iterations perform optimization on the task
for k in range(num_iterations):
#get the minibatch x and y
for i in range(0, num_samples, mini_batch):
#sample mini batch of examples
x_minibatch = x_sample[i:i+mini_batch]
y_minibatch = y_sample[i:i+mini_batch]
train = sess.run(optimizer, feed_dict={X: x_minibatch.reshape(mini_batch,1),
Y: y_minibatch.reshape(mini_batch,1)})
#get the updated model parameters after several iterations of optimization
new_w1, new_b1, new_w2, new_b2 = sess.run([w1, b1, w2, b2])
#Now we perform meta update
#i.e theta = theta + epsilon * (theta_star - theta)
epsilon = 0.1
updated_w1 = old_w1 + epsilon * (new_w1 - old_w1)
updated_b1 = old_b1 + epsilon * (new_b1 - old_b1)
updated_w2 = old_w2 + epsilon * (new_w2 - old_w2)
updated_b2 = old_b2 + epsilon * (new_b2 - old_b2)
#update the model parameter with new parameters
w1.load(updated_w1, sess)
b1.load(updated_b1, sess)
w2.load(updated_w2, sess)
b2.load(updated_b2, sess)
if e%10 == 0:
loss = sess.run(loss_function, feed_dict={X: x_sample.reshape(num_samples,1), Y: y_sample.reshape(num_samples,1)})
print "Epoch {}: Loss {}\n".format(e,loss)
print 'Updated Model Parameter Theta\n'
print 'Sampling Next Batch of Tasks \n'
print '---------------------------------\n'
您可以看到如下输出:
Epoch 0: Loss 13.0675544739
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 10: Loss 7.3604927063
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 20: Loss 4.35141277313
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
总结
在本章中,我们学习了元 SGD 和 Reptile 算法。 我们看到了元 SGD 与 MAML 有何不同,以及如何在监督学习和强化学习设置中使用元 SGD。 我们看到了元 SGD 如何学习模型参数以及学习率和更新方向。 我们还了解了如何从头开始构建元 SGD。 然后,我们了解了 Reptile 算法。 我们看到了 Reptile 与 MAML 的不同之处,以及 Reptile 对 MAML 算法的改进。 我们还学习了如何在正弦波回归任务中使用 Reptile。
在下一章中,我们将学习如何将梯度一致性用作元学习中的优化目标。
问题
- 元 SGD 与 MAML 有何不同?
- 元 SGD 如何找到最佳学习率?
- 元 SGD 中学习率的更新方程是什么?
- Reptile 算法如何工作?
- Reptile 算法的更新方程是什么?
进一步阅读
八、作为优化目标的梯度一致性
在上一章中,我们了解了元 SGD 和 Reptile 算法。 我们看到了如何使用元 SGD 查找最佳参数,最佳学习率和梯度更新方向。 我们还看到了 Reptile 算法的工作原理以及比 MAML 更有效的方法。 在本章中,我们将学习如何将梯度一致性用作元学习的优化目标。 正如您在 MAML 中所看到的,我们基本上是对各个任务的梯度进行平均,并更新模型参数。 在梯度一致性算法中,我们将对梯度进行加权平均以更新模型参数,并且我们将了解如何为梯度添加权重如何帮助我们找到更好的模型参数。 在本章中,我们将确切探讨梯度一致性算法的工作原理。 我们的梯度一致性算法可以同时插入 MAML 和 Reptile 算法。 我们还将从头开始了解如何在 MAML 中实现梯度一致性。
在本章中,我们将学习以下内容:
- 梯度一致性
- 权重计算
- 梯度一致性算法
- 使用 MAML 构建梯度一致性算法
作为优化的梯度一致性
梯度一致性算法是一种有趣且最近引入的算法,可作为元学习算法的增强功能。 在 MAML 和 Reptile 中,我们尝试找到一个更好的模型参数,该参数可在多个相关任务中推广,以便我们可以使用更少的数据点快速学习。 如果我们回顾前面几章中学到的知识,就会发现我们随机初始化了模型参数,然后从任务分布p(T)中抽取了一批随机任务T[i]进行了采样。 对于每个采样任务T[i],我们通过计算梯度将损失降到最低,并获得更新的参数θ'[i],这形成了我们的内部循环:
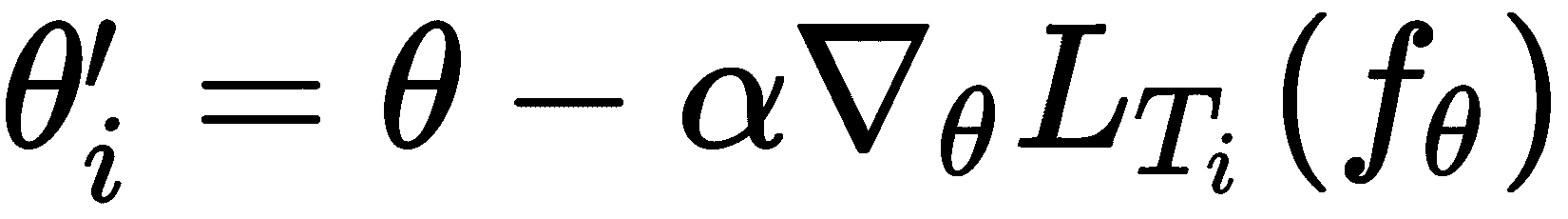
在为每个采样任务计算出最佳参数之后,我们执行元优化-也就是说,我们通过计算一组新任务中的损失来执行元优化,并通过针对最佳参数θ'[i]计算梯度来最大程度地减少损失, 我们在内部循环中获得的,并更新了初始模型参数θ:

前面的方程式实际上是什么? 如果仔细研究这个方程,您会注意到我们只是对各个任务的梯度求平均值,并更新我们的模型参数θ,这意味着所有任务在更新我们的模型参数方面均做出同等贡献。
但是,这怎么了? 假设我们已经采样了四个任务,并且三个任务在一个方向上具有梯度更新,但是一个任务在一个方向上与其他任务完全不同的梯度更新。 由于所有任务的坡度对更新模型参数的贡献均相等,因此这种分歧可能会对更新模型的初始参数产生严重影响。 如下图所示,与其他任务相比,从T[1]到T[3]的所有任务在一个方向上具有梯度,但是任务T[4]在完全不同的方向上具有梯度:
那么,我们现在该怎么办? 我们如何才能了解哪个任务具有很强的梯度一致性,哪些任务具有很强的分歧性? 如果将权重与梯度相关联,是否可以理解其重要性? 因此,我们通过将权重乘以每个梯度来重写外部梯度更新方程,如下所示:

好的,我们如何计算这些权重? 这些权重与任务梯度的内积和采样批量任务中所有任务的梯度平均值的乘积成正比。 但这意味着什么?
它暗示,如果任务的梯度与采样的一批任务中所有任务的平均梯度在同一方向上,则我们可以增加其权重,以便为更新模型参数做出更大的贡献。 同样,如果任务的梯度方向与采样的任务批量中所有任务的平均梯度方向大不相同,则我们可以降低其权重,以便在更新模型参数时贡献较小 。 我们将在下一节中看到如何精确计算这些权重。
我们不仅可以将梯度一致性算法应用于 MAML,还可以应用于 Reptile 算法。 因此,我们的 Reptile 更新方程如下:

权重计算
我们已经看到,通过将权重与梯度相关联,我们可以了解哪些任务具有强梯度一致性,哪些任务具有强梯度不一致。
我们知道,这些权重与任务梯度和采样任务批量中所有任务的梯度平均值的内积成正比。 我们如何计算这些权重?
权重计算如下:

假设我们抽样了一批任务。 然后,对于批量中的每个任务,我们对k个数据点进行采样,计算损失,更新梯度,并找到每个任务的最佳参数θ'[i]。 与此同时,我们还将每个任务的梯度更新向量存储在g[i]中。 可以计算为g[i] = θ - θ'[i]。
因此,第i个任务的权重是g[i]和g[j]的内积之和除以归一化因子。 归一化因子与g[i]和g_avg的内积成正比。
通过查看以下代码,让我们更好地理解如何精确计算这些权重:
for i in range(num_tasks):
g = theta - theta_[i]
#calculate normalization factor
normalization_factor = 0
for i in range(num_tasks):
for j in range(num_tasks):
normalization_factor += np.abs(np.dot(g[i].T, g[j]))
#calcualte weights
w = np.zeros(num_tasks)
for i in range(num_tasks):
for j in range(num_tasks):
w[i] += np.dot(g[i].T, g[j])
w[i] = w[i] / normalization_factor
算法
现在,让我们看一下梯度一致性的工作原理:
- 假设我们有一个由参数
θ参数化的模型f和任务上的分布p(T)。 首先,我们随机初始化模型参数θ。 - 我们从任务分布
T ~ p(T)中采样了一些任务T[i]。 假设我们采样了两个任务,然后是T。 - 内循环:对于任务(
T)中的每个任务(T[i]),我们对k个数据点进行采样,并准备训练和测试数据集:


我们使用梯度下降来计算损失并使D_train[i]上的损失最小,并获得最佳参数θ'[i]:
 。
。
与此同时,我们还将梯度更新向量存储为:g[i] = θ - θ'[i]。
因此,对于每个任务,我们对k个数据点进行采样,并最大程度地减少训练集D_train[i]上的损失,并获得最佳参数θ'[i]。 当我们采样两个任务时,我们将有两个最佳参数θ'[i],并且我们将为这两个任务中的每一个都有一个梯度更新向量g = {(θ - θ'[1]), (θ - θ'[2])}。
- 外循环:现在,在执行元优化之前,我们将按以下方式计算权重:

在计算权重之后,我们现在通过将权重与梯度相关联来执行元优化。 通过计算相对于上一步中获得的参数的梯度,并将梯度与权重相乘,我们将D_test[i]中的损失最小化。
如果我们的元学习算法是 MAML,则更新公式如下:

如果我们的元学习算法是 Reptile,则更新方程如下:
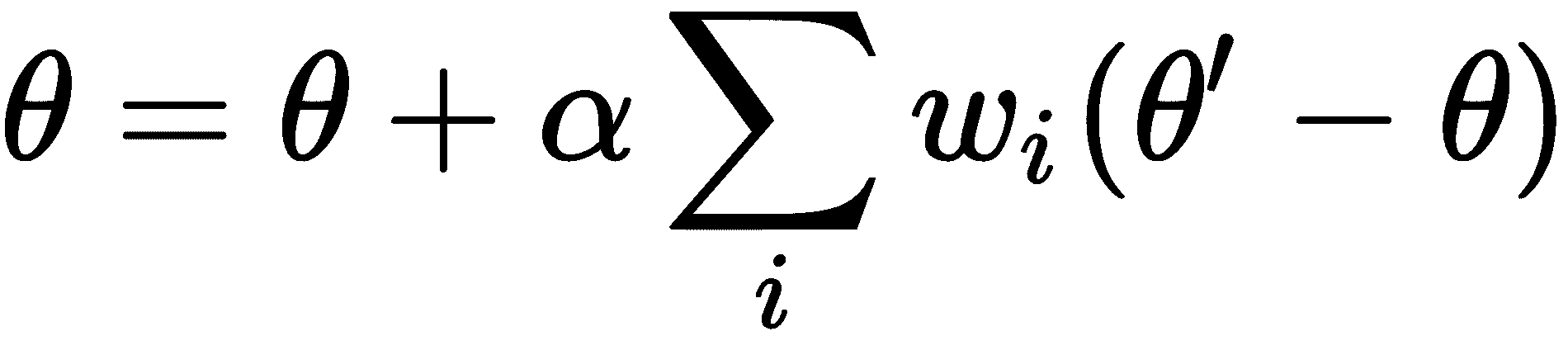
- 对于
n次迭代,我们重复步骤 2 至 5。
使用 MAML 构建梯度一致性算法
在上一节中,我们看到了梯度一致性算法的工作原理。 我们看到了梯度一致性如何为梯度增加权重,从而说明其重要性。 现在,我们将看到如何通过使用 NumPy 从头开始对它们进行编码,从而将梯度一致性算法与 MAML 结合使用。 为了更好地理解,我们将考虑一个简单的二分类任务。 我们将随机生成输入数据,使用简单的单层神经网络对其进行训练,然后尝试找到最佳参数θ。
现在,我们将逐步详细地了解如何执行此操作。
您也可以在此处以 Jupyter 笔记本的形式查看完整代码。
我们导入所有必要的库:
import numpy as np
生成数据点
现在,我们定义了一个名为sample_points的函数,用于生成输入(x, y)对。 它以参数k作为输入,这意味着我们要采样的(x, y)对的数量:
def sample_points(k):
x = np.random.rand(k,50)
y = np.random.choice([0, 1], size=k, p=[.5, .5]).reshape([-1,1])
return x,y
单层神经网络
为了简单起见和更好地理解,我们使用只有一层的神经网络来预测输出:
a = np.matmul(X, theta)
YHat = sigmoid(a)
因此,我们将梯度一致性与 MAML 结合使用,以找到可在各个任务之间通用的最佳参数值theta。 这样一来,对于一项新任务,我们可以通过采取较少的梯度步骤,在较短的时间内从几个数据点中学习。
MAML 中的梯度一致性
现在,我们将定义一个名为GradientAgreement_MAML的类,在其中将实现梯度一致性 MAML 算法。 在__init__方法中,我们将初始化所有必需的变量。 然后,我们将定义 Sigmoid 激活函数。 接下来,我们将定义train函数。
让我们一步一步看一下,然后看一下整体代码:
class GradientAgreement_MAML(object):
我们定义__init__方法并初始化所有变量:
def __init__(self):
#initialize number of tasks i.e number of tasks we need in each batch of tasks
self.num_tasks = 2
#number of samples i.e number of shots -number of data points (k) we need to have in each task
self.num_samples = 10
#number of epochs i.e training iterations
self.epochs = 100
#hyperparameter for the inner loop (inner gradient update)
self.alpha = 0.0001
#hyperparameter for the outer loop (outer gradient update) i.e meta optimization
self.beta = 0.0001
#randomly initialize our model parameter theta
self.theta = np.random.normal(size=self.pol_ord).reshape(self.pol_ord, 1)
现在,我们定义一个名为sigmoid的函数,用于将x转换为多项式形式:
def sigmoid(self,a):
return 1.0 / (1 + np.exp(-a))
现在,让我们定义一个称为train的函数进行训练:
def train(self):
对于周期数,我们执行以下操作:
for e in range(self.epochs):
self.theta_ = []
#for storing gradient updates
self.g = []
对于一批任务中的任务i,我们执行以下操作:
for i in range(self.num_tasks):
我们对k个数据点进行采样,并准备我们的训练集D_train[i]:
XTrain, YTrain = sample_points(self.num_samples)
我们预测YHat的值:
a = np.matmul(XTrain, self.theta)
YHat = self.sigmoid(a)
我们使用梯度下降计算损失并使损失最小化:

#since we're performing classification, we use cross entropy loss as our loss function
loss = ((np.matmul(-YTrain.T, np.log(YHat)) - np.matmul((1 -YTrain.T), np.log(1 - YHat)))/self.num_samples)[0][0]
#minimize the loss by calculating gradients
gradient = np.matmul(XTrain.T, (YHat - YTrain)) / self.num_samples
#update the gradients and find the optimal parameter theta' for each of tasks
self.theta_.append(self.theta - self.alpha*gradient)
我们将梯度更新存储在g和g[i] = θ - θ'中:
self.g.append(self.theta-self.theta_[i])
现在,我们计算权重:
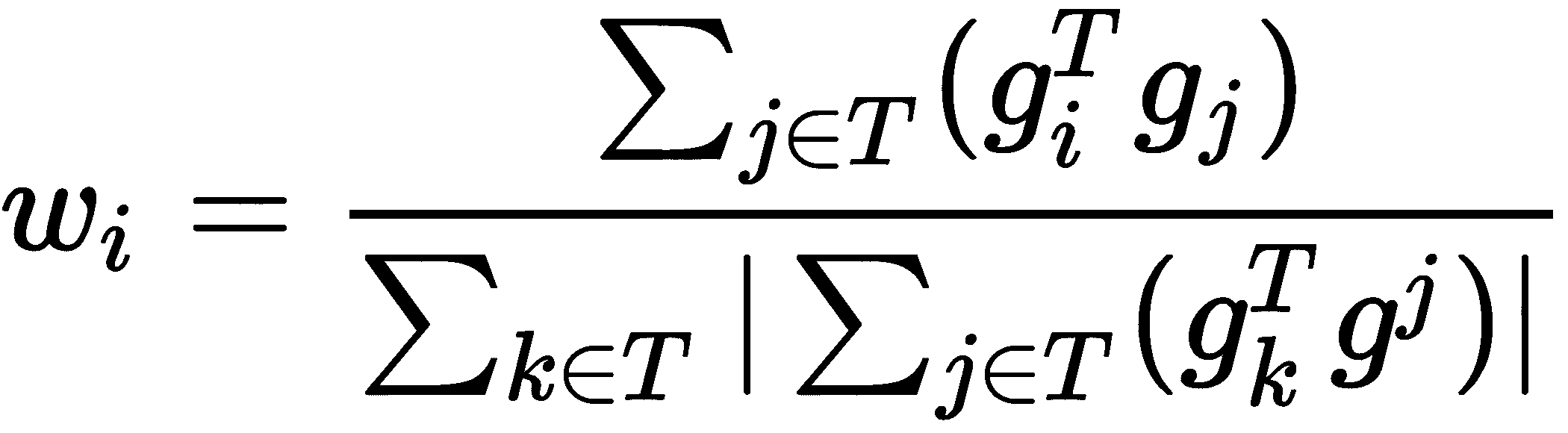
normalization_factor = 0
for i in range(self.num_tasks):
for j in range(self.num_tasks):
normalization_factor += np.abs(np.dot(self.g[i].T, self.g[j]))
w = np.zeros(self.num_tasks)
for i in range(self.num_tasks):
for j in range(self.num_tasks):
w[i] += np.dot(self.g[i].T, self.g[j])
w[i] = w[i] / normalization_factor
我们初始化加权元梯度:
weighted_gradient = np.zeros(self.theta.shape)
对于任务数量,我们对k个数据点进行采样,并准备测试集D_test[i]:
for i in range(self.num_tasks):
#sample k data points and prepare our test set for meta training
XTest, YTest = sample_points(10)
我们预测y的值:
a = np.matmul(XTest, self.theta_[i])
YPred = self.sigmoid(a)
我们计算元梯度:
meta_gradient = np.matmul(XTest.T, (YPred - YTest)) / self.num_samples
将权重乘以计算出的元梯度,并使用这个更新θ的值:

weighted_gradient += np.sum(w[i]*meta_gradient)
self.theta = self.theta-self.beta*weighted_gradient/self.num_tasks
我们每 10 个周期打印一次损失:
if e%10==0:
print "Epoch {}: Loss {}\n".format(e,loss)
print 'Updated Model Parameter Theta\n'
print 'Sampling Next Batch of Tasks \n'
print '---------------------------------\n'
以下是GradientAgreement_MAML的整个类:
class GradientAgreement_MAML(object):
def __init__(self):
#initialize number of tasks i.e number of tasks we need in each batch of tasks
self.num_tasks = 2
#number of samples i.e number of shots -number of data points (k) we need to have in each task
self.num_samples = 10
#number of epochs i.e training iterations
self.epochs = 100
#hyperparameter for the inner loop (inner gradient update)
self.alpha = 0.0001
#hyperparameter for the outer loop (outer gradient update) i.e meta optimization
self.beta = 0.0001
#randomly initialize our model parameter theta
self.theta = np.random.normal(size=50).reshape(50, 1)
#define our sigmoid activation function
def sigmoid(self,a):
return 1.0 / (1 + np.exp(-a))
#now Let's get to the interesting part i.e training :P
def train(self):
#for the number of epochs,
for e in range(self.epochs):
self.theta_ = []
#for storing gradient updates
self.g = []
#for task i in batch of tasks
for i in range(self.num_tasks):
#sample k data points and prepare our train set
XTrain, YTrain = sample_points(self.num_samples)
a = np.matmul(XTrain, self.theta)
YHat = self.sigmoid(a)
#since we're performing classification, we use cross entropy loss as our loss function
loss = ((np.matmul(-YTrain.T, np.log(YHat)) - np.matmul((1 -YTrain.T), np.log(1 - YHat)))/self.num_samples)[0][0]
#minimize the loss by calculating gradients
gradient = np.matmul(XTrain.T, (YHat - YTrain)) / self.num_samples
#update the gradients and find the optimal parameter theta' for each of tasks
self.theta_.append(self.theta - self.alpha*gradient)
#compute the gradient update
self.g.append(self.theta-self.theta_[i])
#now we calculate the weights
#we know that weight is the sum of dot product of g_i and g_j divided by a normalization factor.
normalization_factor = 0
for i in range(self.num_tasks):
for j in range(self.num_tasks):
normalization_factor += np.abs(np.dot(self.g[i].T, self.g[j]))
w = np.zeros(self.num_tasks)
for i in range(self.num_tasks):
for j in range(self.num_tasks):
w[i] += np.dot(self.g[i].T, self.g[j])
w[i] = w[i] / normalization_factor
#initialize meta gradients
weighted_gradient = np.zeros(self.theta.shape)
for i in range(self.num_tasks):
#sample k data points and prepare our test set for meta training
XTest, YTest = sample_points(10)
#predict the value of y
a = np.matmul(XTest, self.theta_[i])
YPred = self.sigmoid(a)
#compute meta gradients
meta_gradient = np.matmul(XTest.T, (YPred - YTest)) / self.num_samples
weighted_gradient += np.sum(w[i]*meta_gradient)
#update our randomly initialized model parameter theta with the meta gradients
self.theta = self.theta-self.beta*weighted_gradient/self.num_tasks
if e%10==0:
print "Epoch {}: Loss {}\n".format(e,loss)
print 'Updated Model Parameter Theta\n'
print 'Sampling Next Batch of Tasks \n'
print '---------------------------------\n'
我们为GradientAgreement_MAML类创建一个实例:
model = GradientAgreement_MAML()
然后,我们训练模型:
model.train()
您会看到损失随着时间的推移而减少:
Epoch 0: Loss 5.9436043239
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 10: Loss 3.905350606769
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 20: Loss 2.0736155578
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
Epoch 30: Loss 1.48478751777
Updated Model Parameter Theta
Sampling Next Batch of Tasks
---------------------------------
总结
在本章中,我们学习了梯度一致性算法。 我们已经看到了梯度一致性算法如何使用加权梯度来找到更好的初始模型参数θ。 我们还看到了这些权重如何与任务梯度的内积和采样批量任务中所有任务的梯度平均值的乘积成正比。 我们还探讨了如何将梯度一致性算法与 MAML 和 Reptile 算法结合使用。 之后,我们看到了如何使用梯度一致性算法在分类任务中找到最佳参数θ'[i]。
在下一章中,我们将了解元学习的最新进展,例如与任务无关的元学习,在概念空间中学习以及元模仿学习。
问题
- 什么是梯度一致性和分歧?
- 梯度一致性中 MAML 的更新方程是什么?
- 梯度一致性中的权重是多少?
- 权重如何计算?
- 什么是归一化因子?
- 我们什么时候增加和减少权重?
进一步阅读
九、最新进展和后续步骤
恭喜你! 我们已经到了最后一章。 我们已经走了很长一段路。 我们从元学习基础开始,然后看到了几种单样本学习算法,例如连体,原型,匹配和关系网络。 后来,我们还看到了 NTM 如何存储和检索信息。 展望未来,我们看到了有趣的元学习算法,例如 MAML,Reptile 和元 SGD。 我们看到了这些算法如何找到最佳的初始参数。 现在,我们将看到元学习的一些最新进展。 我们将学习如何使用与任务无关的元学习来减少元学习中的任务偏差,以及如何在模仿学习系统中使用元学习。 然后,我们将看到如何使用 CACTUs 算法在无监督的学习环境中应用 MAML。 稍后,我们将学习一种称为学习在概念空间中学习的深度元学习算法。
在本章中,您将了解以下内容:
- 任务无关的元学习(TAML)
- 元模仿学习
- CACTUS
- 概念空间的学习
任务不可知元学习(TAML)
我们知道,在元学习中,我们在相关任务的分布上训练模型,以便只需几个样本就可以轻松地将其适应于新任务。 在前面的章节中,我们已经了解了 MAML 如何通过计算元梯度和执行元优化来找到模型的最佳初始参数。 但是我们可能面临的问题之一是,我们的模型可能会偏向某些任务,尤其是在元训练阶段中采样的任务。 因此,我们的模型在这些任务上将表现不佳。 如果模型这样做,那么还将导致我们发现更好的更新规则的问题。 由于在某些任务上存在偏见模型,我们也将无法对与元训练任务有很大差异的未见任务进行更好的概括。
为了减轻这种情况,我们需要使我们的模型在某些任务上不会偏见或表现不佳。 也就是说,我们需要使我们的模型与任务无关,以便可以防止任务偏差并获得更好的概括性。 现在,我们将看到两种执行 TAML 的算法:
- 熵最大化/减少
- 不平等最小化
熵最大化/减少
在本节中,我们将看到如何通过最大化和最小化熵来防止任务偏差。 我们知道熵是对随机性的一种度量。 因此,我们通过允许模型以相等的概率对预测的标签进行随机猜测来最大化熵。 通过对预测标签进行随机猜测,我们可以防止任务偏差。
我们如何计算熵? 让我们用H表示熵。 通过从p[T[i]](x[i])中,在其N个预测标签的输出概率y[i, n]上,抽取x[i]来计算T[i]的熵:

在先前的等式中,y_hat[i]是模型的预测标签。
因此,我们在更新模型参数之前将熵最大化。 接下来,我们在更新模型参数后最小化熵。 那么,最小化熵意味着什么呢? 使熵最小化意味着我们不对预测标签添加任何随机性,并且允许模型以高置信度预测标签。
因此,我们的目标是最大程度地减少每个任务的熵减少量,其表示如下:

我们将熵项与元目标合并,并尝试找到最佳参数θ'[i],因此我们的元目标变为:

并且λ是这两项之间的平衡系数。
算法
现在,我们将逐步了解熵 TAML 的工作原理:
- 假设我们有一个由参数
θ参数化的模型f,并且有一个任务分布p(T)。 首先,我们随机初始化模型参数θ。 - 从任务分布(即
T[i] ~ p(T))中抽样一批任务。 假设我们然后采样了三个任务:T = {T[1], T[2], T[3]}。 - 内循环:对于任务
T中的每个任务T[i],我们对k个数据点进行采样,并准备训练和测试数据集:

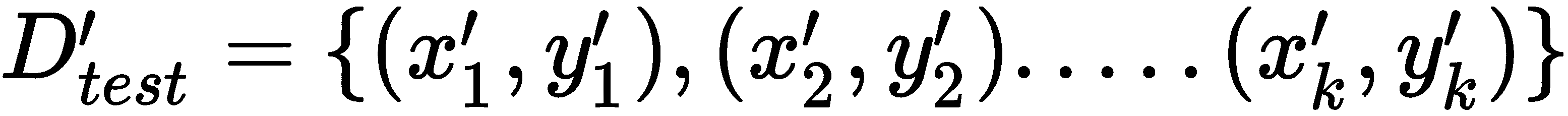
然后,我们在训练集D_train上计算损失,使用梯度下降将损失最小化,并获得最佳参数:

因此,对于每个任务,我们对k个数据点进行采样,准备训练数据集,最大程度地减少损失,并获得最佳参数。 由于我们采样了三个任务,因此我们将拥有三个最佳参数:θ' = {θ'[1], θ'[2], θ'[3]}。
- 外循环:我们执行元优化。 在这里,我们尝试将元训练集
D_test[i]的损失降到最低。 我们通过计算相对于最佳参数θ'[i]的梯度来最小化损失,并更新随机初始化的参数θ; 与此同时,我们将添加熵项。 因此,我们最终的元目标变为:

- 对于
n次迭代,我们重复步骤 2 至 4。
不平等最小化
熵方法的问题在于它仅适用于分类任务。 因此,我们无法将算法应用于回归或强化学习任务。 为了克服这个问题,我们将看到另一种算法,称为不平等最小化 TAML。 就像熵方法一样简单。 在这种方法中,我们试图使不平等最小化。 经济学中使用了几种不平等措施来衡量收入分配,财富分配等。 在元学习环境中,我们可以使用这些经济不平等措施来最小化我们的任务偏差。 因此,可以通过最小化批量中所有采样任务损失的不平等性来最小化模型对任务的偏见。
不平等度量
我们将看到一些常用的不平等测度。 我们可以将任务T[i]中的损失定义为l[i],将采样任务的平均损失定义为l_bar,将单个批量中的任务数定义为M。
基尼系数
这是最广泛使用的不平等衡量标准之一。 它使用洛伦兹曲线测量分布的不等式。 洛伦兹曲线是一条累积频率曲线,它将特定变量的分布与表示等式的均匀分布进行比较。 基尼系数的值介于 0 到 1 之间,其中 0 表示完全相等,而 1 的值表示不完全。 它基本上是相对绝对均值差的一半。
因此,在我们的元学习设置中,我们可以如下计算基尼系数:

泰尔指数
泰尔指数是另一种常用的不平等度量。 它以荷兰计量经济学家 Henri Theil 的名字命名,是不平等度量族的一个特例,称为广义熵度量。 可以将其定义为最大熵与观察到的熵之差。
我们为元学习设置计算泰尔指数,如下所示:

算法的方差
算法的方差可以定义如下:

在先前的等式中,g(l)表示l的几何平均值。
我们可以使用任何这些不平等度量来计算任务偏差。 因此,一旦我们使用此不平等度量来计算任务偏差,就可以通过将不平等度量插入元目标中来最小化偏差。 因此,我们可以如下重写元目标:

在前面的等式中,I(L[T[i]](f[θ'[i]]))代表我们的不平等测度,λ是平衡系数。
算法
现在,我们将逐步了解不平等最小化 TAML 的工作原理:
- 假设我们有一个由参数
θ参数化的模型!f,并且在任务分布p(T)上。 首先,我们随机初始化模型参数θ。 - 我们从任务分布(即
T[i] ~ p(T))中抽样一批任务。 说,我们已经采样了三个任务,然后是T = {T[1], T[2], T[3]}。 - 内循环:对于任务
T中的每个任务T[i],我们对k个数据点进行采样,并准备训练和测试数据集:

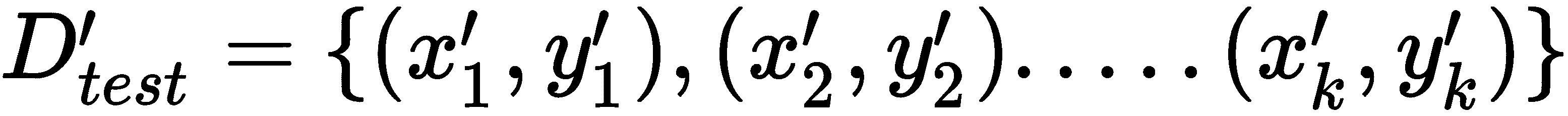
然后,我们在训练集D_train上计算损失,使用梯度下降使损失最小化,并获得最佳参数:
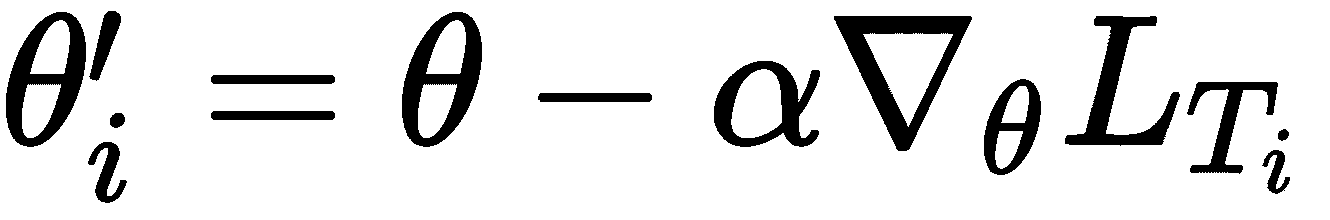
因此,对于每个任务,我们对k个数据点进行采样,准备训练数据集,最大程度地减少损失,并获得最佳参数。 由于我们采样了三个任务,因此我们将拥有三个最佳参数θ' = {θ'[1], θ'[2], θ'[3]}。
- 外循环:现在,我们执行元优化。 在这里,我们尝试使训练集
D_test[i]的损失最小化。 我们通过计算相对于最佳参数θ'[i]的梯度来最小化损失,并更新随机初始化的参数θ; 与此同时,我们将添加熵项。 因此,我们最终的元目标变为:

- 对于
n次迭代,我们重复步骤 2 至 4。
元模仿学习
如果我们希望我们的机器人更具通用性并执行各种任务,那么我们的机器人应该快速学习。 但是,如何使我们的机器人快速学习呢? 好吧,我们人类如何快速学习? 我们不是仅通过看着其他人就轻松地学习新技能吗? 同样,如果我们仅通过观察动作就能使机器人学习,那么我们就可以轻松地使机器人有效地学习复杂的目标,而不必设计复杂的目标和奖励函数。 这种类型的学习(即从人类行为中学习)称为模仿学习,在这种情况下,机器人会尝试模仿人类行为。 机器人并不需要真正从人类的动作中学到东西。 它还可以从执行任务的其他机器人或执行任务的人/机器人的视频中学习。
但是模仿学习并不像听起来那样简单。 机器人将花费大量时间和演示来学习目标并确定正确的策略。 因此,我们将以演示(训练数据)的先验经验丰富机器人,从而不必完全从头学习每种技能。 增强机器人的先验经验有助于其快速学习。 因此,要学习多种技能,我们需要为每种技能收集演示-也就是说,我们需要为机器人添加特定于任务的演示数据。
但是,如何使我们的机器人从单个演示中快速学习一项任务呢? 我们可以在这里使用元学习吗? 我们可以重用演示数据并从几个相关任务中学习以快速学习新任务吗? 因此,我们将元学习和模仿学习相结合,形成元模仿学习(MIL)。 借助 MIL,我们可以利用其他各种任务的演示数据,仅需一个演示就可以快速学习新任务。 因此,我们仅需演示一个新任务就可以找到正确的策略。
对于 MIL,我们可以使用我们已经看到的任何元学习算法。 我们将使用 MAML 作为元学习算法,该算法与可以通过梯度下降训练的任何算法兼容,并且将使用策略梯度作为找到正确策略的算法。 在策略梯度中,我们使用某些参数θ直接优化参数化策略π[θ]。
我们的目标是从单个任务的演示中学习可以快速适应新任务的策略。 这样,我们可以消除对每个任务的大量演示数据的依赖。 实际上,我们在这里的任务是什么? 我们的任务将包含轨迹。 轨迹tr包含来自专家策略的一系列观察和动作,这些经验和活动均是演示。 等待。 什么是专家策略? 由于我们正在执行模仿学习,因此我们正在向专家(人类行为)学习,因此我们将该策略称为专家策略,并以π*表示:

好吧,我们的损失函数应该是什么? 损失函数表示我们的机器人动作与专家动作有何不同。 对于连续动作,我们可以使用均方误差损失作为我们的损失函数,对于离散动作,我们可以使用交叉熵作为损失函数。 假设我们有连续的行动; 那么我们可以如下表示均方误差损失:

假设我们有任务分布p(T)。 我们对一批任务进行采样,对于每个任务T[i],我们对一些演示数据进行采样,通过最小化损失来训练网络,并找到最佳参数θ'[i]。 接下来,我们通过计算元梯度执行元优化,并找到最佳初始参数θ。 我们将在下一部分中确切地了解它的工作方式。
MIL 算法
MIL 中涉及的步骤如下:
-
假设我们有一个由参数
θ参数化的模型f,并且有一个任务分布p(T)。 首先,我们随机初始化模型参数θ。 -
从任务分布(即
T ~ p(T))中抽样一些任务T[i]。 -
内循环:对于采样任务中的每个任务,我们都采样了一个演示数据-即
trajectory = {o1, a1, ..., o[t], a[t]}。 现在,我们通过执行梯度下降来计算损失并将损失降至最低,从而获得了最佳参数θ'[i]:
然后,我们还为元训练采样了另一个演示数据:
trajectory' = {o'1, a'1, ..., o'[t], a'[t]}。 -
外循环:现在,我们通过元优化使用
trajectory'更新我们的初始参数,如下所示:

- 对
n次迭代重复步骤 2 到 4。
CACTUS
我们已经了解了 MAML 如何帮助我们找到最佳的初始模型参数,以便可以将其推广到许多其他相关任务。 我们还了解了 MAML 如何在监督学习和强化学习设置中使用。 但是,我们如何在没有数据点标签的无监督学习环境中应用 MAML? 因此,我们引入了一种称为 CACTUS 的新算法,该算法是Clustering to Automatically Generate Tasks for Unsupervised Model Agnostic Meta Learning的缩写。
假设我们有一个数据集D,其中包含未标记的示例:D = {x[1], ..., x[n]}。 现在,我们可以使用该数据集做什么? 我们如何在该数据集上应用 MAML? 首先,使用 MAML 进行训练需要什么? 我们需要按任务分布,并通过对一批任务进行采样并找到最佳模型参数来训练模型。 任务应包含特征及其标签。 但是,如何从未标记的数据集中生成任务?
在下一部分中,让我们看看如何使用 CACTUS 生成任务。 生成任务后,我们可以轻松地将其插入 MAML 算法并找到最佳模型参数。
使用 CACTU 生成任务
假设我们有一个数据集D,其中包含没有标签的样本:D = {x[1], ..., x[n]}。 现在我们需要为数据集创建标签。 我们该怎么做? 首先,我们使用一些嵌入函数来学习数据集中每个数据点的嵌入。 嵌入函数可以是任何特征提取器。 假设我们的输入是一幅图像,那么我们可以使用 CNN 作为嵌入函数来提取图像特征向量。
为每个数据点生成嵌入后,我们如何找到它们的标签? 朴素的和简单的方法是将我们的数据集D划分为具有某些随机超平面的p个分区,然后我们可以将数据集的每个这些分区子集视为一个单独的类。
但是这种方法的问题在于,由于我们使用的是随机超平面,因此我们的类可能包含完全不同的嵌入,并且还将相关的嵌入保留在不同的类中。 因此,我们可以使用聚类算法来代替使用随机超平面对数据集进行分区。 我们使用 k 均值聚类作为我们的聚类算法来划分数据集。 我们对多个迭代运行 k-means 聚类,并获得k聚类(分区)。
我们可以将每个群集视为一个单独的类。 下一个是什么? 我们如何生成任务? 假设由于集群,我们有五个集群。 我们从这五个群集中采样n个群集。 然后,我们从n个群集的每个中抽取r数据点,而无需替换; 这可以表示为{x[r]}_n。 之后,我们对n个单任务特定标签l[n]进行了排列,以为n个采样聚类的每一个分配标签。 因此,现在我们有一个数据点{x[r]}_n和一个标签l[n]。
最后,我们可以将任务T定义为:
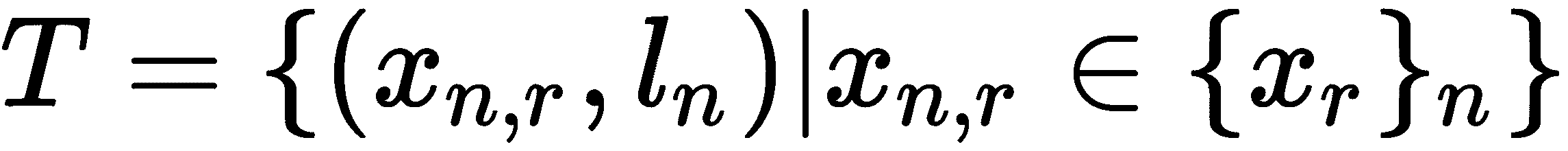
概念空间中的元学习
现在,我们将看到如何使用深度元学习在概念空间中元学习。 首先,我们如何进行元学习? 我们在每个任务中抽样一批相关任务和一些k数据点,并训练我们的元学习器。 我们可以将深度学习的力量与元学习结合起来,而不仅仅是使用我们的原始元学习技术进行训练。 因此,当我们对一批任务以及每个任务中的一些k数据点进行采样时,我们将使用深度神经网络学习每个k数据点的表示形式,然后对这些表示进行元学习。
我们的框架包含三个组件:
- 概念生成器
- 概念判别器
- 元学习器
概念生成器的作用是提取数据集中每个数据点的特征表示,捕获其高级概念,概念判别器的作用是识别和分类由概念生成器生成的概念,而元学习器学习由概念生成器生成的概念。 先前的所有组件(即概念生成器,概念判别器和元学习器)都可以一起学习。 因此,我们通过将元学习与深度学习相集成来改善原始元学习。 我们的概念生成器随着新的传入数据而发展,因此我们可以将我们的框架视为终身学习系统。
但是这里到底发生了什么? 看下图; 如您所见,我们对一组任务进行采样,并将其提供给概念生成器,该概念生成器将学习概念(即嵌入),然后将这些概念提供给元学习器,后者将学习这些概念并将损失回馈给概念生成器。 同时,我们还将一些外部数据集提供给概念生成器,概念生成器学习这些输入的概念并将这些概念发送给概念识别器。 概念识别器预测这些概念的标签,计算损失,然后将损失发送回概念生成器。 通过这样做,我们增强了概念生成器概括概念的能力:

但是,为什么我们要这样做呢? 代替在原始数据集上执行元学习,我们在概念空间中执行元学习。 我们如何学习这些概念? 这些概念由概念生成器通过学习输入的嵌入来生成。 因此,我们在各种相关任务上训练概念生成器和元学习器; 与此相伴的是,我们通过向概念生成器提供外部数据集,从而通过概念判别器改进了概念生成器,以便可以更好地学习概念。 通过联合训练过程,我们的概念生成器可以学习各种概念并在相关任务上表现更好; 我们输入外部数据集只是为了增强概念生成器的表现,当我们输入一组新的输入时,它会不断学习。 因此,这是一个终身学习系统。
关键组件
现在,让我们详细了解每个组件。
概念生成器
众所周知,概念生成器用于提取特征。 我们可以使用由某些参数θ[G]参数化的深度神经网络来生成概念。 例如,如果我们的输入是图像,则概念生成器可以是 CNN。
概念判别器
它基本上是一个分类器,用于预测概念生成器生成的概念的标签。 因此它可以是由θ[D]参数化的任何监督学习算法,例如 SVM 和决策树。
元学习器
我们的元学习器可以是θ[M]参数化的任何元学习算法,例如 MAML,元 SGD 或 Reptile。
损失函数
我们在这里使用两组损失函数:
- 概念判别损失
- 元学习损失
概念判别损失
我们从数据集D中采样一些数据点(x, y),将它们馈送到概念生成器,该概念生成器学习概念并将其发送给概念判别器,后者试图预测这些概念的类。 因此,概念判别器的损失意味着我们的概念判别器在预测类别方面有多出色,可以表示为:

根据我们的任务,损失函数可以是任何损失函数。 例如,如果我们执行分类任务,则可能是交叉熵损失。
元学习损失
我们从任务分布中抽样一些任务,通过概念生成器学习它们的概念,对这些概念执行元学习,然后计算元学习损失:

我们的元学习损失取决于我们使用的元学习器,例如 MAML 或 Reptile。
我们的最终损失函数是概念歧视和元学习损失这两者的组合:
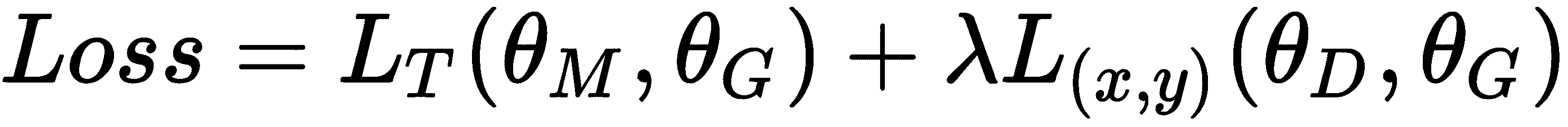
在前面的等式中,lambda是元学习和概念歧视损失之间的超参数平衡。 因此,我们的目标是找到使此损失最小的最佳参数:

我们通过计算梯度来最小化损失并更新模型参数:

算法
现在,我们将逐步了解我们的算法:
- 假设我们有一个任务分布
p(T)。 首先,我们随机初始化模型参数,例如概念生成器θ[G],元学习器θ[M]和概念判别器θ[D]的参数。 - 我们从任务分布中抽样一批任务,并通过概念生成器学习它们的概念,对这些概念执行元学习,然后计算元学习损失:

- 我们从外部数据集
D中采样一些数据点(x, y),将它们馈送到概念生成器以学习其概念,将这些概念馈送到概念判别器中,对它们进行分类,然后计算概念辨别损失:

- 我们将这两种损失合并在一起,并尝试使用 SGD 来使损失最小化,并获取更新的模型参数:

- 对
n次迭代重复步骤 2 到 4。
再次恭喜您学习了所有重要且流行的元学习算法。 元学习是 AI 的一个有趣且最有前途的领域,它将使我们更接近广义人工智能(AGI)。 现在,您已经阅读完本书,可以开始探索元学习的各种进步,并开始尝试各种项目。 学习和元学习!
总结
在本章中,我们学习了 TAML 来减少任务偏差。 我们看到了两种类型的方法:基于熵的 TAML 和基于不等式的 TAML。 然后,我们探索了元模仿学习,它将元学习与模仿学习相结合。 我们看到了元学习如何帮助模仿学习从更少的模仿中学习。 我们还看到了如何在使用 CACTUS 的无监督学习环境中应用模型不可知元学习。 然后,我们探索了一种称为学习在概念空间中学习的深度元学习算法。 我们看到了深度学习的力量如何促进元学习。
元学习是 AI 领域中最有趣的分支之一。 既然您已经了解了各种元学习算法,那么您就可以开始构建可在各种任务中推广的元学习模型,并为元学习研究做出贡献。
问题
- 什么是不平等度量的所有不同类型?
- 什么叫泰尔指数?
- 什么是模仿学习?
- 什么是概念生成器?
- 什么是元学习损失?
进一步阅读
十、答案
第 1 章:元学习简介
- 元学习产生了一种通用的 AI 模型,该模型可以学习执行各种任务,而无需从头开始进行训练。 我们使用几个数据点在各种相关任务上训练我们的元学习模型,因此对于新的但相关的任务,该模型可以利用从先前任务中学到的知识而不必从头开始进行训练。
- 从更少的数据点学习称为少样本学习或 K 样本学习,其中
k表示在数据集的每个类别中的数据点的数量。 - 为了使我们的模型从一些数据点中学习,我们将以相同的方式对其进行训练。 因此,当我们有一个数据集
D时,我们从数据集中存在的每个类中采样一些数据点,并将其称为支持集。 - 我们从与支持集不同的每个类中采样不同的数据点,并将其称为查询集。
- 在基于度量的元学习设置中,我们将学习适当的度量空间。 假设我们要找出两个图像之间的相似性。 在基于度量的设置中,我们使用一个简单的神经网络,该网络从两个图像中提取特征并通过计算这两个图像的特征之间的距离来查找相似性。
- 我们以剧情方式训练模型; 也就是说,在每个剧情中,我们从数据集
D中采样一些数据点,并准备我们的支持集并在支持集上学习。 因此,在一系列事件中,我们的模型将学习如何从较小的数据集中学习。
第 2 章:使用连体网络的人脸和音频识别
-
连体网络是神经网络的一种特殊类型,它是最简单,最常用的单样本学习算法之一。 连体网络基本上由两个对称的神经网络组成,它们具有相同的权重和架构,并最终通过能量函数
E结合在一起。 -
对比损失函数可以表示为:
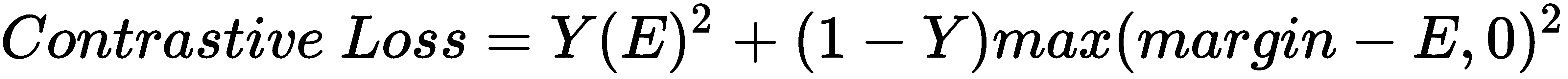
在前面的公式中,
Y的值是真实的标签,当两个输入值相似时为 1,如果两个输入值不相似则为 0,而E为我们的能量函数,可以是任何距离度量。 术语边距用于保持约束; 也就是说,当两个输入值不相同且它们之间的距离大于边距时,则不会造成损失。 -
能量函数告诉我们两个输入的相似程度。 它基本上是任何相似性度量,例如欧几里得距离和余弦相似性。
-
连体网络的输入应该成对
(X1, X2)及其二进制标记Y ∈ (0, 1),指出输入对是真实对(相同)还是非真实对(不同)。 -
连体网络的应用是无止境的。 它们已经堆叠了用于执行各种任务的各种架构,例如人类动作识别,场景更改检测和机器翻译。
第 3 章:原型网络及其变体
- 原型网络简单,高效,是最常用的少量学习算法之一。 原型网络的基本思想是创建每个类的原型表示形式,并根据类原型和查询点之间的距离对查询点(新点)进行分类。
- 我们为每个数据点计算嵌入来学习特征。
- 一旦我们了解了每个数据点的嵌入,就可以将每个类中数据点的均值嵌入并形成类原型。 因此,类原型基本上就是在类中数据点的平均嵌入。
- 在高斯原型网络中,连同为数据点生成嵌入,我们在它们周围添加一个置信区域,该区域由高斯协方差矩阵表征。 拥有置信区域有助于表征单个数据点的质量,并且对于嘈杂且不太均匀的数据很有用。
- 高斯原型网络与原始原型网络的不同之处在于,在原始原型网络中,我们仅学习数据点的嵌入,但在高斯原型网络中,除了学习嵌入之外,我们还为其添加了置信区域。
- 半径和对角线是高斯原型网络中使用的协方差矩阵的不同组成部分。
第 4 章:使用 TensorFlow 的关系和匹配网络
-
关系网络由两个重要函数组成:嵌入函数(由
f[φ]表示)和关系函数由g[φ]表示。 -
有了支持集
f[φ](x[i])和查询集f[φ](x[j])的特征向量后,就可以使用运算符Z组合它们。 在这里,Z可以是任何组合运算符; 我们使用连接作为运算符来组合支持集和查询集的特征向量: 。
。 -
关系函数
g[φ]将生成一个介于 0 到 1 之间的关系评分,代表支持集x[i]中的样本与查询集中x[j]中的样本之间的相似性。 -
我们的损失函数可以表示为:

-
在匹配网络中,我们使用两个嵌入函数
f和g分别学习查询集x_hat和支持集y_hat的嵌入。 -
查询点
x_hat的输出y_hat可以预测如下:
第 5 章:记忆增强神经网络
-
NTM 是一种有趣的算法,能够存储和检索内存中的信息。 NTM 的想法是通过外部存储器来增强神经网络-也就是说,它不是使用隐藏状态作为存储器,而是使用外部存储器来存储和检索信息。
-
控制器基本上是前馈神经网络或循环神经网络。 它从内存读取和写入。
-
读头和写头是包含其必须读取和写入的内存地址的指针。
-
内存矩阵或内存库,或者简称为内存,是我们存储信息的地方。 内存基本上是由内存单元组成的二维矩阵。 内存矩阵包含
N行和M列。 使用控制器,我们可以从内存中访问内容。 因此,控制器从外部环境接收输入,并通过与存储矩阵进行交互来发出响应。 -
基于位置的寻址和基于内容的寻址是 NTM 中使用的不同类型的寻址机制。
-
插值门用于决定是否应使用上一时间步获得的权重
w[t - 1]或使用通过基于内容的寻址获得的权重w[t]^c。 -
从使用权重向量
w[t]^u计算最少使用的权重向量w[t]^(lu)非常简单。 我们仅将最低值使用权重向量的索引设置为 1,将其余值设置为 0,因为使用权重向量中的最小值表示最近使用最少。
第 6 章:MAML 及其变体
- MAML 是最近引入且最常用的元学习算法之一,它已导致元学习研究取得重大突破。 MAML 的基本思想是找到更好的初始参数,以便具有良好的初始参数,模型可以以更少的梯度步骤快速学习新任务。
- MAML 与模型无关,这意味着我们可以将 MAML 应用于可通过梯度下降训练的任何模型。
- ADML 是 MAML 的一种变体,它同时利用干净样本和对抗样本来查找更好且更可靠的初始模型参数θ。
- 在 FGSM 中,我们获得了图像的对抗样本,并计算了相对于图像的损失梯度,更清楚地输入了图像的像素而不是模型参数。
- 上下文参数是特定于任务的参数,该参数在内部循环中更新。 用 denoted 表示,它特定于每个任务,代表单个任务的嵌入。
- 共享参数在任务之间共享,并在外循环中更新以找到最佳模型参数。 用θ表示。
第 7 章:元 SGD 和 Reptile 算法
-
与 MAML 不同,在元 SGD 中,除了找到最佳参数值
θ之外,我们还找到最佳学习率α并更新方向。 -
学习率在适应项中隐式实现。 因此,在元 SGD 中,我们不会以较小的标量值初始化学习率。 相反,我们使用与
θ相同形状的随机值初始化它们,然后与θ一起学习它们。 -
学习率的更新公式可以表示为:

-
对
n个任务进行采样,并在每个采样任务上以较少的迭代次数运行 SGD,然后按照所有任务共有的方向更新模型参数。 -
Reptile 更新方程可表示为
θ = θ + ε(θ' - θ)。
第 8 章:作为优化目标的梯度一致性
-
当所有任务的梯度都在同一方向上时,则称为梯度一致性;当某些任务的梯度与其他任务之间存在较大差异时,则称为梯度不一致。
-
梯度一致性中的更新方程可表示为:
 。
。 -
权重与任务梯度的内积和采样任务批量中所有任务的梯度平均值成正比。
-
权重计算如下:

-
归一化因子与
g[i]和g_avg的内积成比例。 -
如果任务的梯度与采样的任务批量中所有任务的平均梯度方向相同,则我们可以增加其权重,以便在更新模型参数时做出更大的贡献。 同样,如果任务的梯度方向与采样的任务批量中所有任务的平均梯度方向大不相同,那么我们可以减小其权重,以便在更新模型参数时其贡献较小。
第 9 章:最新进展和后续步骤
-
不平等度量的不同类型是基尼系数,泰尔指数和算法的方差。
-
泰尔指数是最常用的不平等度量。 它是以荷兰计量经济学家 Henri Theil 的名字命名的,是不平等度量族的一种特例,称为广义熵度量。 可以将其定义为最大熵与观察到的熵之差。
-
如果我们仅通过观察动作就能使机器人学习,那么我们就可以轻松地使机器人有效地学习复杂的目标,而不必设计复杂的目标和奖励函数。 这种类型的学习(即从人类行为中学习)称为模仿学习,在这种情况下,机器人会尝试模仿人类行为。
-
概念生成器用于提取特征。 我们可以使用由某些参数
θ[G]参数化的深度神经网络来生成概念。 例如,如果我们的输入是图像,则概念生成器可以是 CNN。 -
我们从任务分布中抽样一批任务,通过概念生成器学习它们的概念,对这些概念执行元学习,然后计算元学习损失:
