343. 整数拆分
题目链接:343. 整数拆分 - 力扣(LeetCode)
思路
动规五部曲,分析如下:
- 确定dp数组(dp table)以及下标的含义
dp[i]:分拆数字 i,可以得到的最大乘积为dp[i]。
- 确定递推公式
可以想 dp[i]最大乘积是怎么得到的呢?
其实可以从1遍历j,然后有两种渠道得到dp[i].
一个是j * (i - j) 直接相乘。
一个是j * dp[i - j],相当于是拆分(i - j),对这个拆分不理解的话,可以回想dp数组的定义。
那有同学问了,j怎么就不拆分呢?
j是从1开始遍历,拆分j的情况,在遍历j的过程中其实都计算过了。那么从1遍历j,比较(i - j) * j和dp[i - j] * j 取最大的。递推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
也可以这么理解,j * (i - j) 是单纯的把整数拆分为两个数相乘,而 j * dp[i - j] 是拆分成两个以及两个以上的个数相乘。( 从 3 开始,数就可以被拆分成三个或三个以上,而有些dp[i]
就可能是通过三个或三个以上相乘获得的结果,此时在相乘 j 就相当于多个数相乘了。)
如果定义dp[i - j] * dp[j] 也是默认将一个数强制拆成4份以及4份以上了。
所以递推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
那么在取最大值的时候,为什么还要比较dp[i]呢?
因为在递推公式推导的过程中,每次计算dp[i],取最大的而已。
- dp的初始化
严格从dp[i]的定义来说,dp[0] dp[1] 就不应该初始化,也就是没有意义的数值。
拆分0和拆分1的最大乘积是多少?
这是无解的。
这里我只初始化dp[2] = 1,从dp[i]的定义来说,拆分数字2,得到的最大乘积是1,这个没有任何异议!
- 确定遍历顺序
确定遍历顺序,先来看看递归公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
dp[i] 是依靠 dp[i - j]的状态,所以遍历i一定是从前向后遍历,先有dp[i - j]再有dp[i]。
1 for (int i = 3; i <= n ; i++) {
2 for (int j = 1; j <= i / 2; j++) { // 也可以为 j < i - 1
3 dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
4 }
5 }
因为拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的。
例如 6 拆成 3 * 3, 10 拆成 3 * 3 * 4。 100的话 也是拆成m个近似数组的子数 相乘才是最大的。
只不过我们不知道m究竟是多少而已,但可以明确的是m一定大于等于2,既然m大于等于2,也就是 最差也应该是拆成两个相同的 可能是最大值。
那么 j 遍历,只需要遍历到 n/2 就可以,后面就没有必要遍历了,一定不是最大值。
- 举例推导dp数组
举例当n为10 的时候,dp数组里的数值,如下:
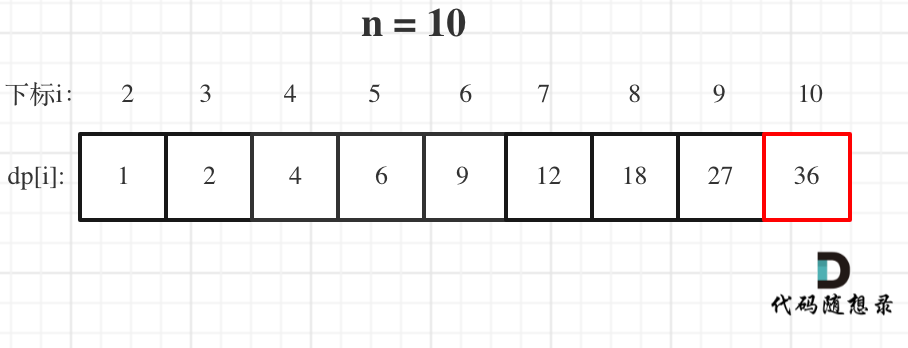
代码
1 class Solution {
2 public int integerBreak(int n) {
3 //dp[i] 为正整数 i 拆分后的结果的最大乘积
4 int[] dp = new int[n+1];
5 dp[2] = 1;
6 for(int i = 3; i <= n; i++) {
7 for(int j = 1; j <= i-j; j++) {
8 // 这里的 j 其实最大值为 i-j,再大只不过是重复而已,
9 //并且,在本题中,我们分析 dp[0], dp[1]都是无意义的,
10 //j 最大到 i-j,就不会用到 dp[0]与dp[1]
11 dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
12 // j * (i - j) 是单纯的把整数 i 拆分为两个数 也就是 i,i-j ,再相乘
13 //而j * dp[i - j]是将 i 拆分成两个以及两个以上的个数,再相乘。
14 }
15 }
16 return dp[n];
17 }
18 }
1 class Solution {
2 /*
3 本题也可以用贪心,每次拆成n个3,如果剩下是4,则保留4,然后相乘,但是这个结论需要数学证明其合理性!
4 */
5 public int integerBreak(int n) {
6 if (n == 2) return 1;
7 if (n == 3) return 2;
8 if (n == 4) return 4;
9 int result = 1;
10 while (n > 4) {
11 result *= 3;
12 n -= 3;
13 }
14 result *= n;
15 return result;
16 }
17 }
96.不同的二叉搜索树
题目链接:96. 不同的二叉搜索树 - 力扣(LeetCode)
思路
了解了二叉搜索树之后,我们应该先举几个例子,画画图,看看有没有什么规律,如图:
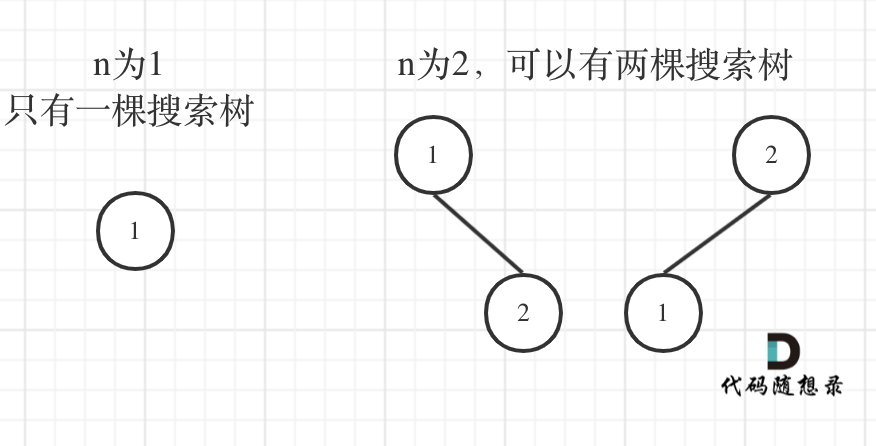
n为1的时候有一棵树,n为2有两棵树,这个是很直观的。
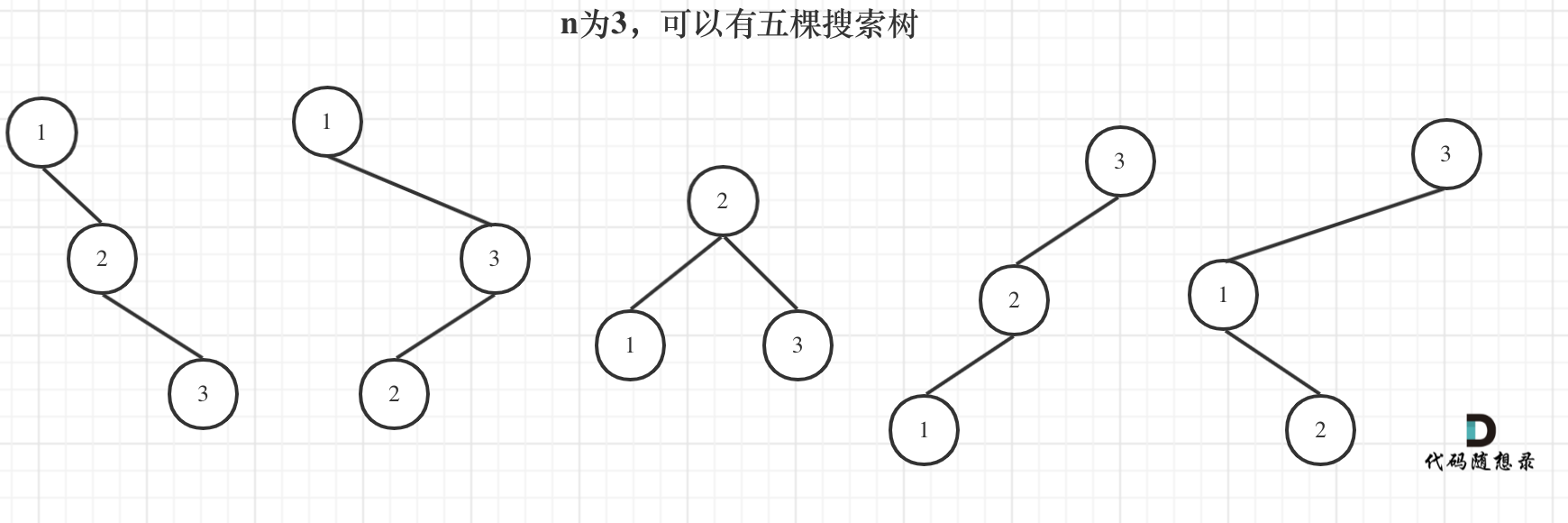
来看看n为3的时候,有哪几种情况。
- 当1为头结点的时候,其右子树有两个节点,看这两个节点的布局,是不是和 n 为2的时候两棵树的布局是一样的啊!(因为我们就是求不同树的数量,并不用把搜索树都列出来,所以不用关心其具体数值的差异)
- 当3为头结点的时候,其左子树有两个节点,看这两个节点的布局,是不是和n为2的时候两棵树的布局也是一样的啊!
- 当2为头结点的时候,其左右子树都只有一个节点,布局是不是和n为1的时候只有一棵树的布局也是一样的啊!
发现到这里,其实我们就找到了重叠子问题了,其实也就是发现可以通过dp[1] 和 dp[2] 来推导出来dp[3]的某种方式;
思考到这里,这道题目就有眉目了。
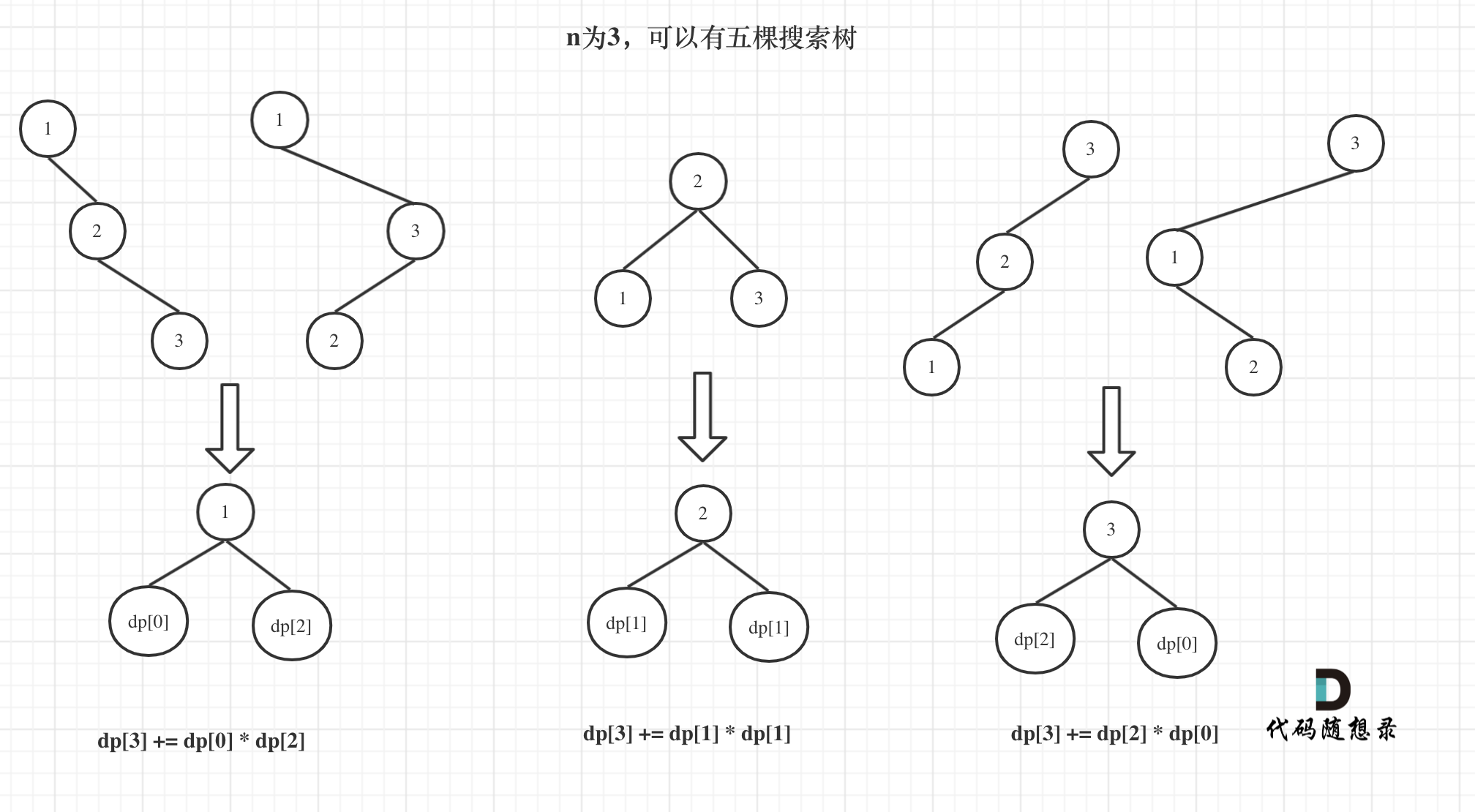
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量;
- 元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
- 元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
- 元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
- 有2个元素的搜索树数量就是dp[2]。
- 有1个元素的搜索树数量就是dp[1]。
- 有0个元素的搜索树数量就是dp[0]。
- 所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
如图所示:
- 确定dp数组(dp table)以及下标的含义
dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]。
- 确定递推公式
在上面的分析中,其实已经看出其递推关系, dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
- dp数组如何初始化
初始化,只需要初始化dp[0]就可以了,推导的基础,都是dp[0]。
那么dp[0]应该是多少呢?
从定义上来讲,空节点也是一棵二叉树,也是一棵二叉搜索树,这是可以说得通的。
从递归公式上来讲,dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0,也需要dp[以j为头结点左子树节点数量] = 1, 否则乘法的结果就都变成0了。
所以初始化dp[0] = 1
- 确定遍历顺序
首先一定是遍历节点数,从递归公式:dp[i] += dp[j - 1] * dp[i - j]可以看出,节点数为i的状态是依靠 i之前节点数的状态。
那么遍历i里面每一个数 ( j ) 作为头结点的状态,用j来遍历。
- 举例推导dp数组
n为5时候的dp数组状态如图:
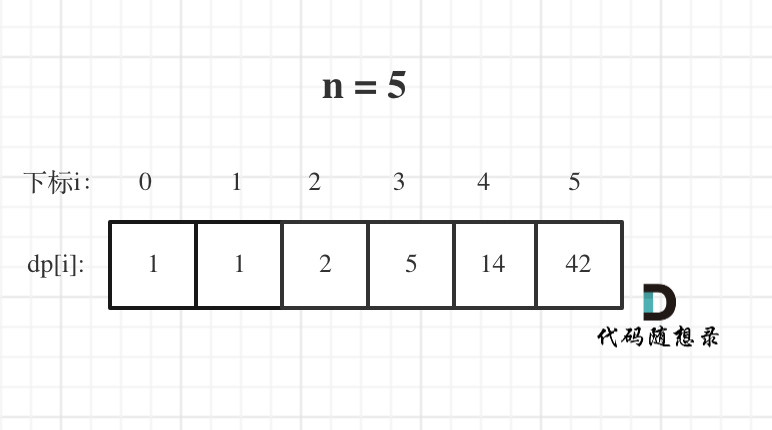
代码
1 class Solution {
2 public int numTrees(int n) {
3 //初始化 dp 数组
4 int[] dp = new int[n + 1];
5 //初始化0个节点和1个节点的情况
6 dp[0] = 1;
7 dp[1] = 1;
8 for (int i = 2; i <= n; i++) {
9 for (int j = 1; j <= i; j++) {
10 //对于第i个节点,需要考虑1作为根节点直到i作为根节点的情况,所以需要累加
11 //一共i个节点,对于根节点j时,左子树的节点个数为j-1,右子树的节点个数为i-j
12 dp[i] += dp[j - 1] * dp[i - j];
13 }
14 }
15 return dp[n];
16 }
17 }
标签:结点,遍历,随想录,搜索,Day41,343,为头,节点,dp From: https://www.cnblogs.com/xpp3/p/17211044.html