首页 > 编程语言 >考研数据结构与算法（七）图论

考研数据结构与算法（七）图论

时间：2022-08-28 22:59:47浏览次数：101  
标签：图论 有向图 1.2 连通 路径 结点 顶点 数据结构 考研

@

目录

一、图的基本概念

1.1 图的定义

图 G 由顶点集 \(V\) 边集 \(E\) 组成，记为 \(G=(V, E)\) ， 其中 \(V(G)\) 表示图 \(G\) 中顶点的有限非空集；
\(E(G)\) 表示图 \(G\) 中顶点之间的关系 （边） 集合。 若 \(V= {V_1 , V_2，…， V_n}\)，则用 \(|V|\) 叫表示图中顶点的个数，也称图 \(G\) 的阶， \(E = {(u,v) \ | \ u∈V,v∈V}\)，用 \(|E|\) 表示图 \(G\) 中边的条数。

注意：图的顶点集 \(V\) 一定为非空，而图的边集 \(E\) 可能为空

1.2 基本术语

1.2.1 有向图

图中的边集是由方向的，例如有一个从点 \(A\) 到 \(B\) 的有向边，那么我们从 \(A\) 点可以到达 \(B\) 点，而不能从 \(B\) 点到达 \(A\) 点，这样就是一个有向边，在这条边中点 \(A\) 被称为 弧尾 ，而点 \(B\) 被称为 弧头 ，我们通常用这样的符号来记录这条边：<A,B>

1.2.2 无向图

很显然没有方向的边和顶点集构成的图就为无向图，按照上面的情况，在无向图中顶点之间是互相连通的，即若有一个点 \(A\) 到点 \(B\) 的边，从 \(B\) 出发也是能到达 \(A\) 点的，我们通常使用这样的符号来记录这条边：(A,B)

1.2.3 简单图

一个图 \(G\) 若满足：

  • ①不存在重复边
  • ②不存在顶点到自身的边，则称图 \(G\) 为简单图

1.2.4 多重图

若图 \(G\) 中某两个结点之间的边数多于一条，又允许顶点通过同一条边也和自己关联，则 \(G\) 为多重图。多重图的定义和简单图是相对的

1.2.5 完全图

  • 在一个顶点数量为 \(n\) 的无向图中，若边的数量为 \(\frac{(n-1)\times n}{2}\) ，则该无向图为完全图
  • 在一个顶点数量为 \(n\) 的有向图中，若边的数量为 \((n-1)\times n\) ，则该有向图为完全图

1.2.6 子图

设有两个图 \(G = (V,E)\) 和 \(G'＝(V',E')\)， 若 \(V'\)是 \(V\) 的子集，且 \(E'\)是 \(E\) 的子集，则称 \(G'\) 是 \(G\) 的子图，若满足 \(V' = V\) 且 \(E' \subset E\) 那么子图 \(G'\) 为 \(G\) 的生成子图

注意：并非 \(V\) 和 \(E\) 的任何子集都能构成 \(G\) 的子图，因为这样的子集可能不是图， 即 \(E\) 的子集中的某些边关联的顶点可能不在这个 \(V\) 的子集中

1.2.7 连通、连通分量、连通图

关于连通方面的定义都是基于无向图的

  • 连通：在无向图中若从顶点 \(u\) 到顶点 \(v\) 有路径存在，那么称 \(u\) 和 \(v\) 是连通的
  • 连通图：若无向图中任意两点是连通的，那么这个无向图就称为连通图，否则称为非连通图
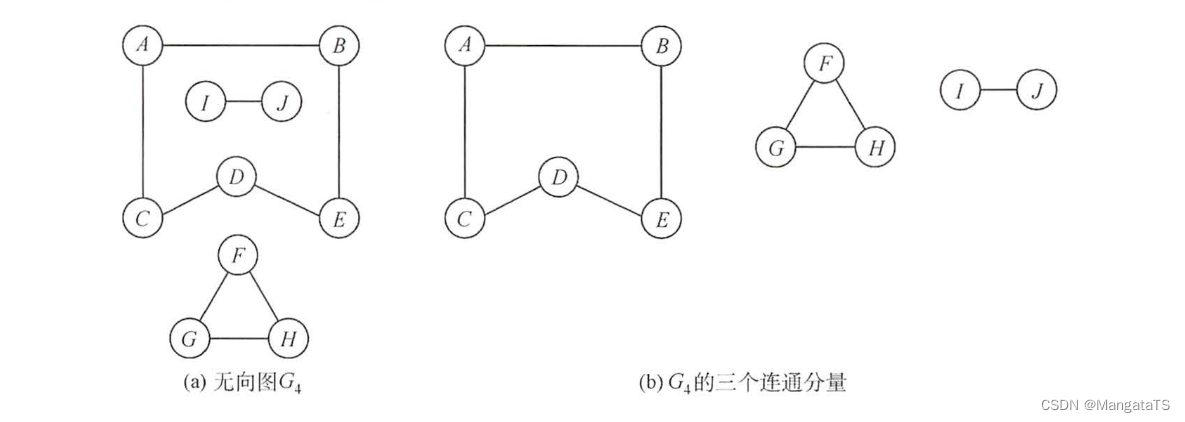
  • 连通分量：对于一个连通图而言，其连通分量只有一个就是其本身，而对于非连通图而言，连通分量有多个，其每一个子图（或者称为极大联通子图）都是一个连通分量

很显然一个 \(n\) 个点的连通图最少有 \(n-1\) 条边（即后面提到的生成树），最多有 \(\frac{(n-1)\times n}{2}\) 个边

这里再补一下 极小连通子图 的定义：一个顶点为 \(n\) 的子图的边数为 \(n-1\) （其实后面也能知道这其实是生成树的定义） ，就称其为极小连通子图，很显然这样的子图也是一个极大连通子图，因为它是一个连通分量。

例如，对于下面的这个非连通图，其连通分量有三个：
在这里插入图片描述

1.2.8 强连通

关于强连通方面的定义都是基于有向图的

  • 强连通：在有向图中，若从顶点 \(v\) 到顶点 \(w\) 和从顶点 \(w\) 到顶点 \(v\) 之间都有路径 ，则称这两个顶点为强连通的
  • 强连通图：若有向图中任意两点之间都是强连通的，那么称这个有向图为强连通图，否则称为非强连通图
  • 强连通分量：对于一个强连通图而言，其强连通分量就是本身，而对于一个非强连通图而言，其极大强连通子图就为该非强连通分量（在子图中任意两点仍满足强连通）

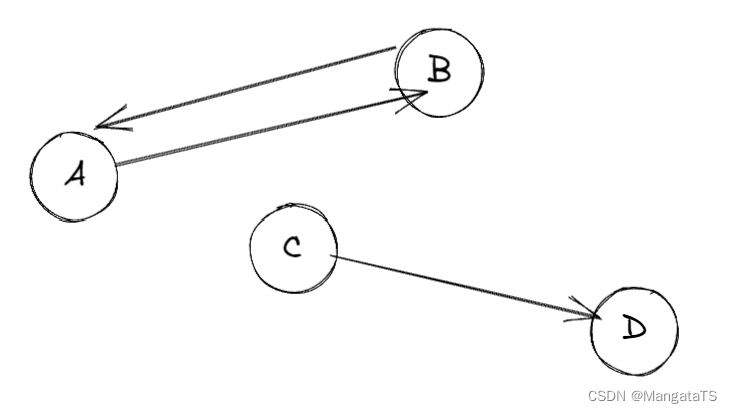
例如，对于如下的非强连通图，其中点 \(A\) 和 \(B\) 构成的子图就为极大联通子图，即强连通分量，而点 \(C\) 和 \(D\) 构成的子图则不是强连通分量
在这里插入图片描述

1.2.9 生成树、森林

生成树、森林一般是基于无向图的

连通图的生成树是包含图中全部顶点的一个极小连通子图，即一个 \(n\) 个点的连通图中有 \(n-1\) 条边

很显然这样的连通图，如果减去一条边就会形成非连通图，而若是加上一条边，则会形成回路

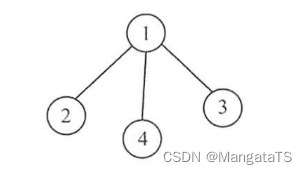
例如，下图中的连通图就为一个生成树：
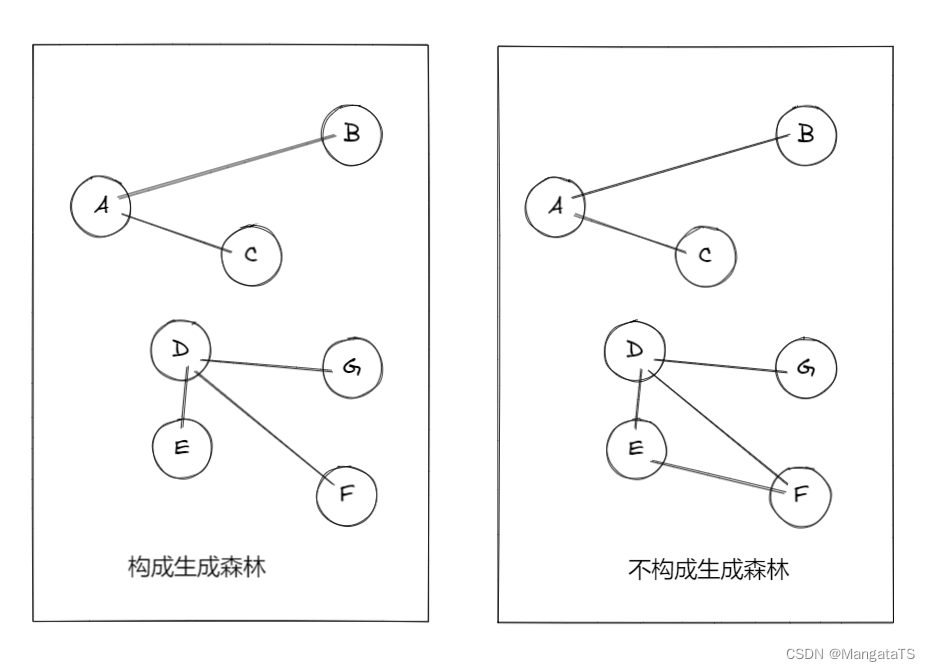
在这里插入图片描述

而生成森林其实就是多个连通子图都是极小连通子图（生成树），那么就称这个森林为生成森林，例如下图中左边森林为生成森林，而右边的森林不是连通森林：
在这里插入图片描述

1.2.10 顶点的度

  • 无向图：对于无向图而言，顶点的度就是和该顶点相连接的边数
  • 有向图：对于有向图而言，指向该顶点的边数称为入度，而从该顶点指出的边数称为出度
  • 无向图的全部顶点的度之和等于两倍的边数
  • 有向图的全部顶点的出度等于全部顶点的入度等于边数

1.2.11 边权和网

在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值。 这种边上带有权值的图称为带权图，也称网 。
网中通常分为， \(AOV\) 网和 \(AOE\) 网

  • \(AOV\) 网：没有权值，或者权值都相同，主要是在于点与点之间的先后关系
  • \(AOE\) 网：有权值，每一个点称为事件，而边称为活动

1.2.12 稠密、稀疏图

  • 稠密图：点数较大，而边数较少的图称为稀疏图
  • 稠密图：点数较小，而边数较多的图称为稠密图

一般来说当图 \(G\) 满足 \(|E| < |V|log_2|V|\) 的时候，可以将图G定义为稀疏图，反之则为稠密图

1.2.13 路径、路径长度、回路

  • 路径：顶点 \(V_u\) 到顶点 \(V_v\) 的顶点序列 \(V_p,V_{i1},V_{i_2},……,V_u\) 称为这两点的路径
  • 路径长度：路径上边的数目称为路径长度
  • 回路：起点和终点相同的非 \(0\) 路径长度的路径称为回路

1.2.14 简单路径、简单回路

  • 简单路径：在路径的顶点序列中顶点不重复的路径称为简单路径
  • 简单回路：除了起点和终点相同外其余顶点不重复的回路称为简单回路

1.2.15 距离

从顶点 \(u\) 出发到顶点 \(v\) 的最短路径若存在，则此路径的长度称为从 \(u\) 到 \(v\) 的距离 。 若从 \(u\) 到 \(ν\) 根本不存在路径，则记该距离为无穷 \((∞)\)

1.2.16 有向树

一个顶点的入度为 \(0\) 、其余顶点的入度均为 \(1\) 的有向图，称为有向树

二、图的存储结构

2.1 邻接矩阵

通过一个一维矩阵 \(V\) 存储顶点信息，然后再通过一个二维矩阵 \(A\) 存储边的信息

对于无权图 \(A[i][j]\) 的含义如下：

\[A[i][j] = \begin{cases} 1 ,若(V_i,V_j)或者 <V_i,V_j>是E(G)中的边 \\ 0 ,若(V_i,V_j)或者 <V_i,V_j>不是E(G)中的边\\ \end{cases} \]

对于有权图 \(A[i][j]\) 的含义如下：

\[A[i][j] = \begin{cases} V[i][j] ,若(V_i,V_j)或者 <V_i,V_j>是E(G)中的边 \\ 0或∞ ,若(V_i,V_j)或者 <V_i,V_j>不是E(G)中的边\\ \end{cases} \]

我们可以将这个结构进行封装为如下形式：

#define MaxVertexNum 100
typedef struct {
	int Vex[MaxVertexNum];//存储当前顶点的表
	int Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵表
	int vexnum, arcnum;//当前的顶点数和弧数
}

邻接矩阵存储表示法的特点：

  • ①无向图的邻接矩阵一定是一个对称矩阵且唯一，因此我们可以使用三角矩阵压缩存储，就能节省一半的空间
  • ②对于无向图邻接矩阵的第 \(i\) 行（列）的非 \(0\) 元素的个数就为第 \(i\) 个顶点的度
  • ③对于有向图邻接矩阵，第 \(i\) 行（列）的非 \(0\) 元素的个数就为第 \(i\) 个顶点的出度（入度）
  • ④邻接矩阵适合存储稠密图

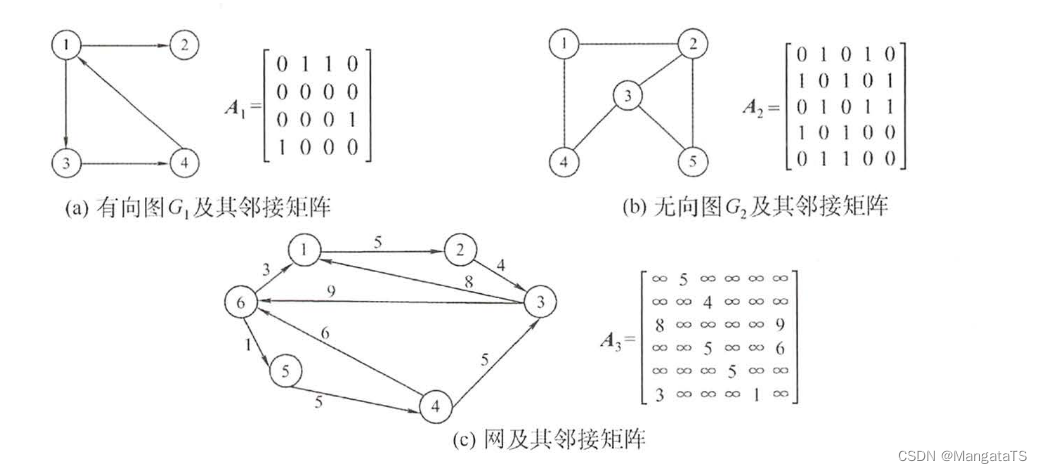
一些通过邻接矩阵存储的图的示例如下：
在这里插入图片描述

2.2 邻接表

我们对图中每一个顶点建一个单链表，然后链表的元素就为其所连接的点，这样就能节省大量的空间，这样的邻接表中存在两种类型的结点：顶点结点、边表结点
在这里插入图片描述
这个顶点结点就类似我们之前的头节点，下面是无向图和有向图的邻接链表的例子：

无向图：
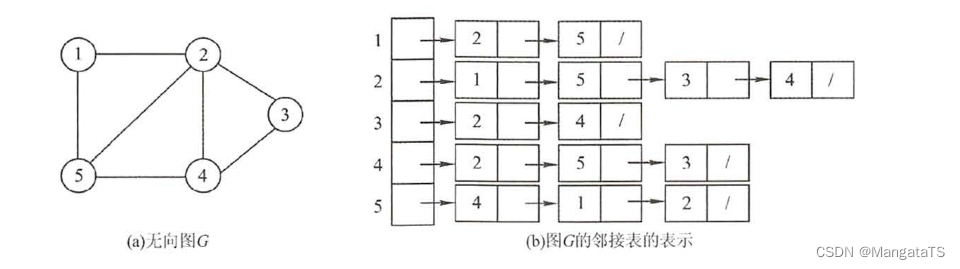
在这里插入图片描述
有向图：
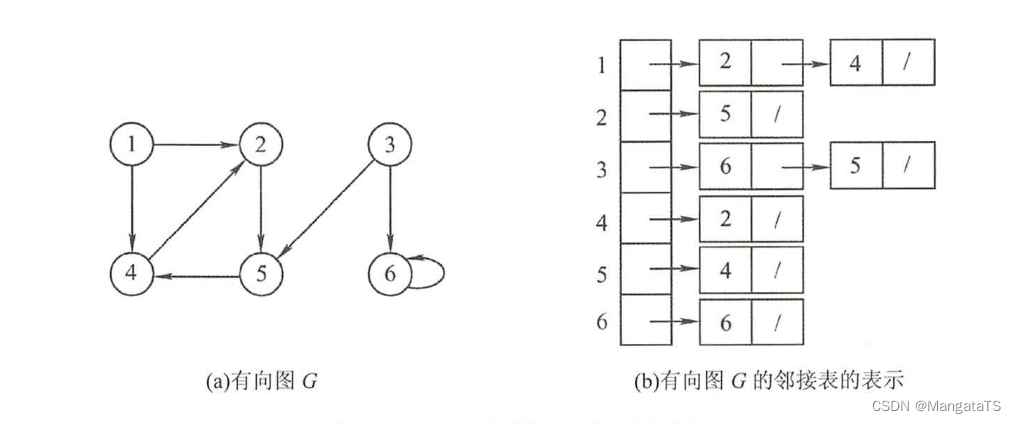
在这里插入图片描述
我们可以简单得到一下这个邻接表的结构：

#define MaxVertexNum 100 
typedef struct ArcNode{ //边表结点
	int adjvex; //该弧指向的顶点的位置
	struct ArcNode *next; //下一条弧的位置
	// infoType info;
}ArcNode; 
typedef struct VNode{ //顶点结点
	VertexType data; //顶点的信息，例如值之类的
	ArcNode *first;//第一个边表结点的位置
}VNode , AdjList[MaxVertexNum]; 
typedef struct{ 
	VNode AdjList[MaxVertexNum]; //顶点结点数组
	int vexnum,arcnum;//顶点数和弧数
} ALGraph;//封装的邻接表的图

邻接表存储方法特点：

  • ①若图 \(G\) 为无向图，则邻接表所需的存储空间为 \(O(|V|+2|E|)\) ，若图 \(G\) 为有向图，则邻接表所需的存储空间为 \(O(|V|+|E|)\)
  • ②邻接表适合稀疏图
  • ③图的邻接表表示不唯一，取决于边的读入顺序

2.3 十字链表

首先来说，十字链表是对于有向图而言的，有一点邻接表和邻接矩阵结合的感觉，首先对于每一个顶点来说有一个顶点结点的概念，然后对于其指向的边结点有一个弧结点的概念

  • 顶点结点有三个域

    • data 域存放顶点相关的数据信息，
    • firstin 域指向以该顶点为弧头的第一个弧结点（比如这个结点是第二个结点，那么就指向第二列，从上往下看的第一个弧节点元素，当然若是没有的话则指向NULL）
    • firstout 域指向以该顶点为弧尾的第一个弧结点（比如这个结点是第三个结点，那么就指向第三行 的第一个弧结点元素）

  • 弧结点有五个域

    • tailvex 尾域表示弧尾的位置（显然对于某一行数据来说，弧尾域都是一样的）
    • headvex 头域表示弧头的位置（显然对于某一列数据来说，弧头域都是一样的）
    • hlink 链域指向弧头相同的下一条弧（其实就是对于每一列的弧结点元素来说，上下相邻的元素从上往下指）
    • tlink 链域指向弧尾相同的下一条弧（其实就是对于每一行的弧结点元素来说，左右相邻的元素从左往右指）
    • info 域一般用于弧的值的存储

例如如下有向图构建的十字链表：
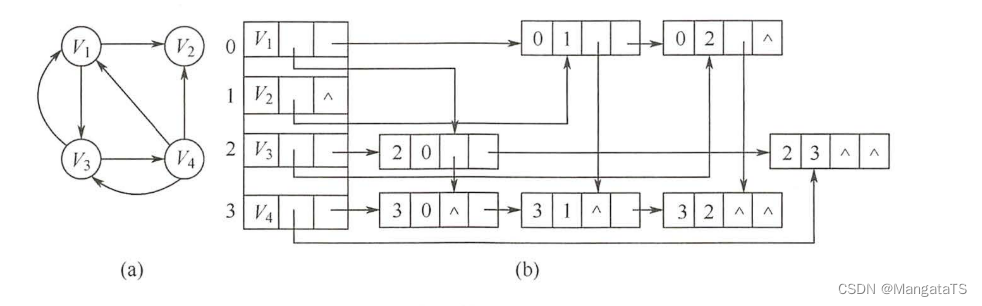
在这里插入图片描述

注意：上图中的弧结点没有info 域

2.4 邻接多重链表

邻接多重表是无向图的另一种链式存储结构，着重于边与边以及边与点的关系，与十字链表类似，邻接多重表也有顶点结点以及边结点

  • 顶点结点有两个域

    • data 域
    • firstedge 用于存储与该结点相连的第一条边

  • 边结点有六个域（但是一般只用其中间的四个）

    • mark 域用于标记这个边是否进行操作过，\(0\) 表示没操作过，\(1\) 表示操作过了
    • ivex 用于表示该边的其中一个结点在图中的下标
    • ilink 用于表示与结点 ivex 相邻的第一条边
    • jvex 用于表示该边的另一个结点在图中的下标
    • jlink 用于表示与结点 jvex 相邻的第一条边
    • info 用于表示该边的一些权值等信息

下面是一些绘制邻接多重表的步骤：

  • ①我们仍然可以先画出该图的邻接表(但不要画箭头)
  • ②因为该图是一个无向图，所以我们需要将重复的边进行删除（统一规划一下可以尽量从往上删除）
  • ③然后从每一个顶点结点出发，指向边结点中与之对应的 \(ilink\) 或者 \(jlink\) 这里的话有两种方式
    • 第一种按照 \(DFS\) 的方法，不断在边结点中找到下一个边结点的位置，直到完成所有的边，再从下一个顶点结点出发
    • 第二种按照 \(BFS\) 的方法，首先找到第一个顶点结点的下一个相邻结点，然后再完成下一个顶点结点，然后再不断完成边界点的关系指向
      例如假设我们有如下的图结构：
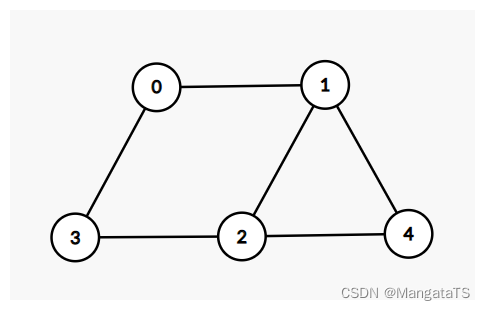
      在这里插入图片描述
      我们需要绘制邻接表，然后删除重复的边：
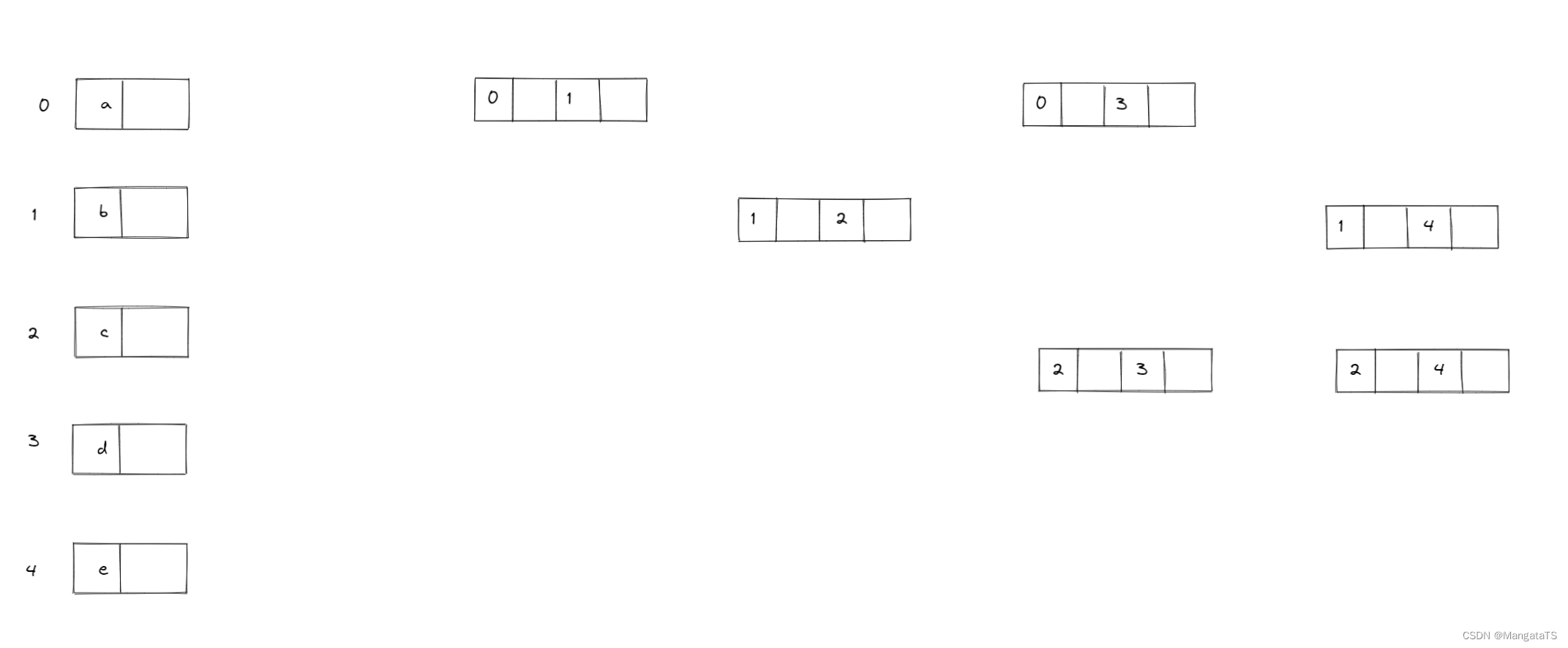
      在这里插入图片描述
      然后我们采用BFS的方法先完成顶点结点的指向
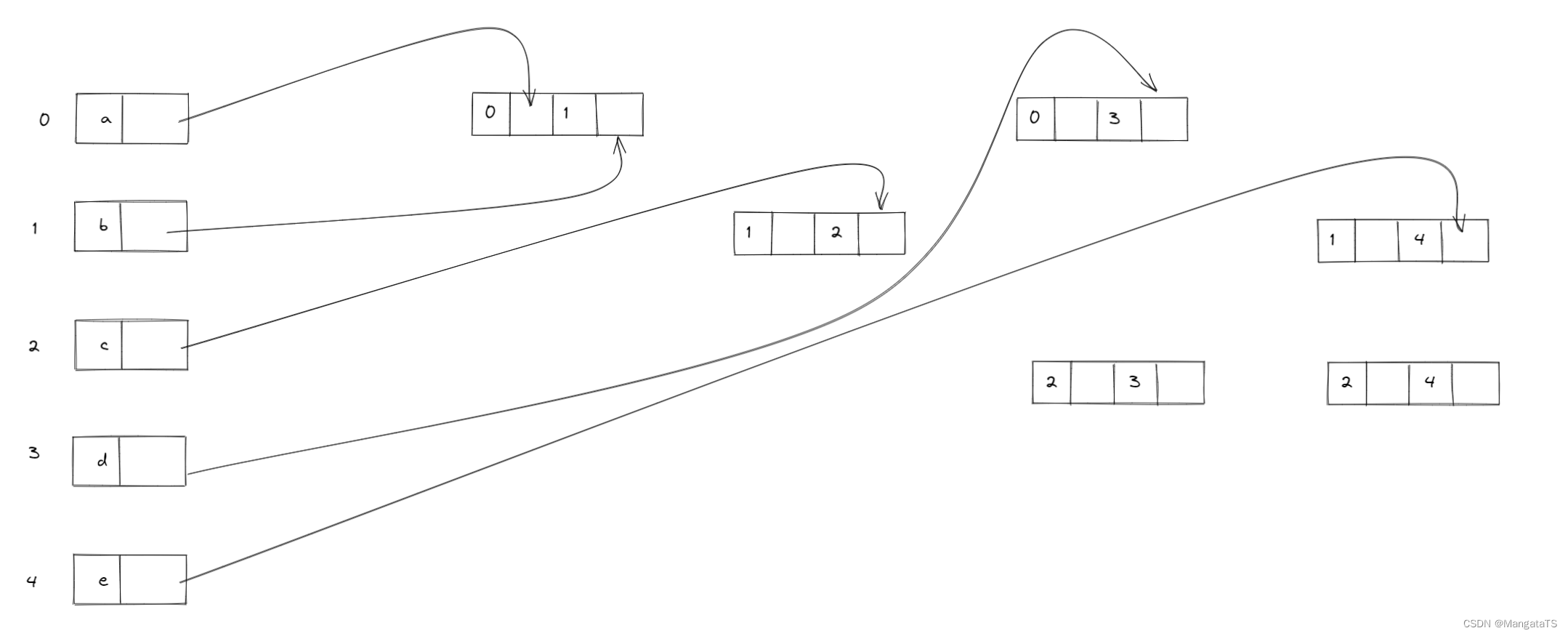
      在这里插入图片描述
      然后就是不断根据边结点进行连接了，于是我们就得到了多重邻接表的画法(当然多重邻接表不一定唯一)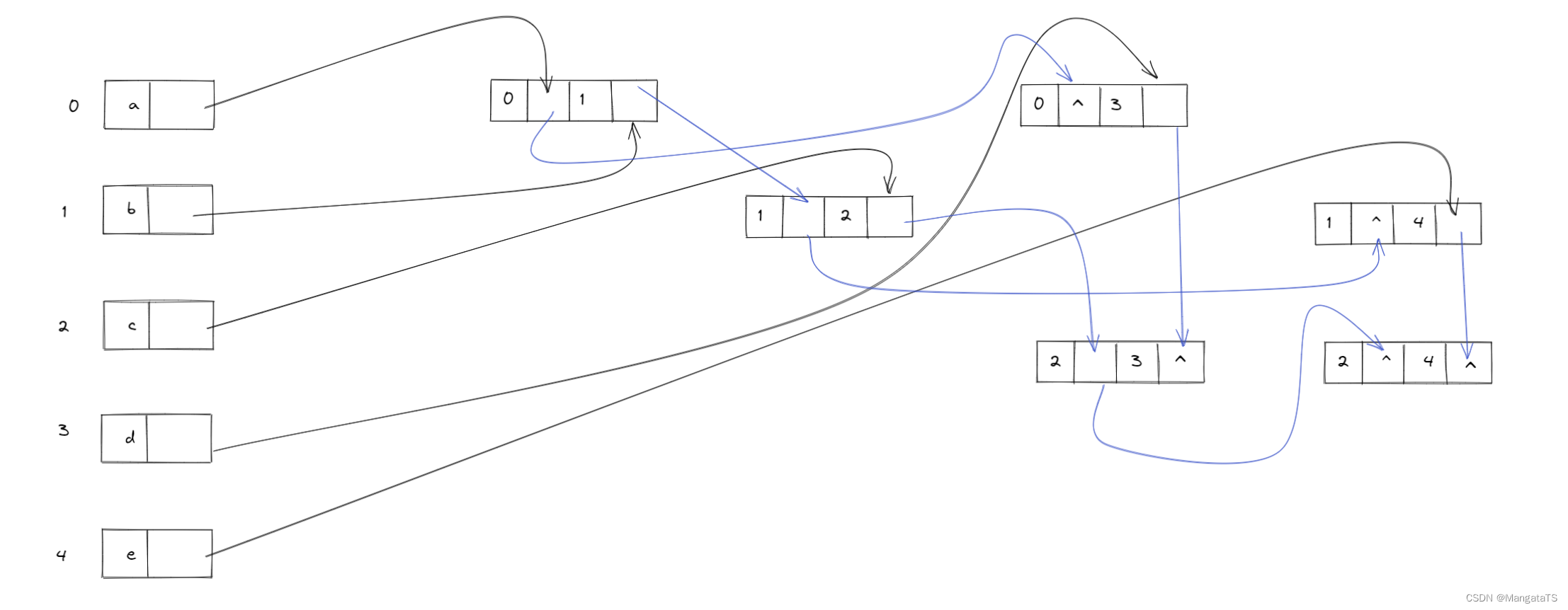在这里插入图片描述

三、图的遍历方法

也可参见我的另一篇介绍：https://acmer.blog.csdn.net/article/details/122310835

3.1 广度优先搜索（BFS）

图的广度优先搜索类似于树的层序遍历，不断地将未访问的结点放入队列，然后出队，再将出队元素所连接的所有未访问点放入队列，这个当队列为空的时候，我们就完成了图的广度优先搜索，简单的搜索如下：

bool vis[N];
void bfs(int s){
	queue<int> que;
	que.push(s);
	vis[s] = true;
	while(!que.empty()){
		int t = que.front();
		que.pop();
		printf("%d\t",t);
		for(int i = 0,l = V[t].size();i < l; ++i) {
			if(!vis[V[t][i]]){
				que.push(V[t][i]);
				vis[V[t][i]] = true;
			}
		}
	}
}

void BFS_Traverse(int n) {
	memset(vis,false,sizeof vis);
	for(int i = 1;i <= n; ++i) {
		if(!vis[i]) bfs(i);
	}
}

当然另一个 \(BFS\) 的例子是求解单源最短路问题，用的是一个以 \(1\) 为源点，然后求得是到 \(n\) 的最短距离（当然边权都为 \(1\) ）

int dis[N];
bool vis[N];
int bfs(){
	memset(dis,0x3f,sizeof dis);
	queue<int> que;
	dis[1] = 0;
	que.push(1);
	vis[1] = true;
	while(!que.empty()){
		int t = que.front();
		que.pop();
		if(t == n)
			return dis[n];
		for(int i = 0,l = V[t].size();i < l; ++i) {
			if(!vis[V[t][i]]){
				que.push(V[t][i]);
				dis[V[t][i]] = dis[t] + 1;
				vis[V[t][i]] = true;
			}
		}
	}
	return -1;
}

ps ：
① 如果是想输出这个最短路径的话，我们可以用一个数组记录每一步的前一个点的位置，然后递归输出一下即可
② 要是想获取层次遍历的结果，只需要在队首元素每次取出的时候输出即可

我们来分析 \(BFS\) 的时间和空间复杂度

  • 邻接矩阵存储：时间复杂度为 \(O(|V|^2) = O(n^2)\) ，空间复杂度为 \(O(|V|) = O(n)\)
  • 邻接表存储：时间复杂度为 \(O(|V| + |E|) = O(n + e)\) ，空间复杂度为 \(O(|V|) = O(n)\)

3.2 深度优先搜索（DFS）

\(DFS\) 即优先深度搜索，可能会从一个点开始往一个方向一直往下搜，然后搜到尽头后就回溯，直到当前连通块的所有的结点全都被搜索过，就停止递归搜索，一般来说 \(DFS\) 的代码都会十分简洁，但是常数耗时会非常大

bool vis[N];//结点被访问情况
vector<int> Edge[N];//存储的边
void DFS(int s){//当前访问的结点
	if(vis[s]) return;
	vis[s] = true;//标记访问
	//do something
	for(int i = 0,l = Edge[s].size();i < l; ++i) {
		int v = Edge[s][i];
		dfs(v);//递归搜索
	}
}

void DFS_Traverse(int n) {
	memset(vis,false,sizeof vis);
	for(int i = 1;i <= n; ++i) {
		if(!vis[i]) dfs(i);
	}
}

我们可以明显看出 \(DFS\) 的代码较为简洁，我们来分析一下 \(DFS\) 的时间复杂度

  • 邻接矩阵存储：时间复杂度为 \(O(|V|^2) = O(n^2)\) ，空间复杂度为 \(O(|V|) = O(n)\)
  • 邻接表存储：时间复杂度为 \(O(|V| + |E|) = O(n + e)\) ，空间复杂度为 \(O(|V|) = O(n)\)

四、图的基本应用

4.1 最小生成树

最小生成树算法在我另一篇博客有较为详细的讲解：
https://acmer.blog.csdn.net/article/details/118560004

4.2 最短路径

最短路径算法在我另一篇博客有较为详细的讲解：（包括Floyd、bellman、SPFA、Dijkstra）

https://acmer.blog.csdn.net/article/details/123040285

4.3 有向无环图描述表达式

有向无环图：字面意思一个不存在环的有向图，简称 \(DAG\) 图
对于一个中缀表达式，我们首先是能够将其转化为二叉树的，例如：对于该表达式 \((a+b)(c-d)\) 的二叉树结构如下：
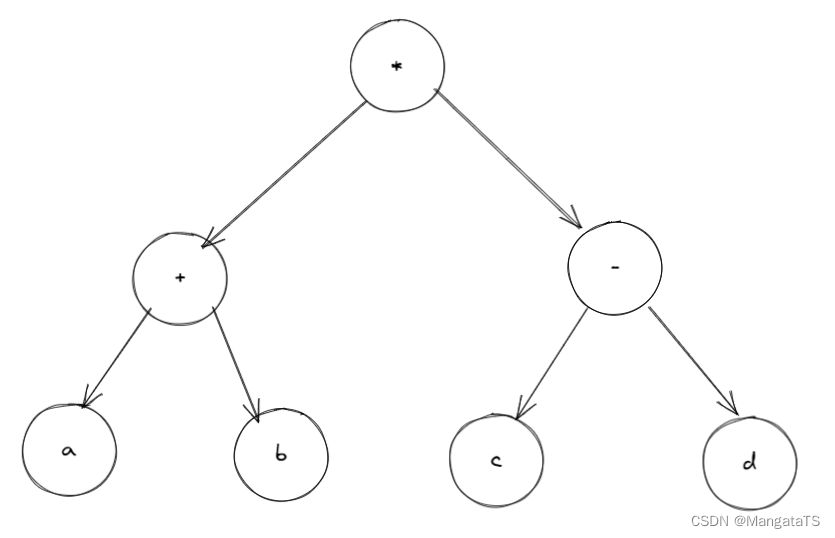
在这里插入图片描述
再来个复杂点的表达式：

\[( ( a + b) * ( b * ( c + d)) + ( c + d) * e) * ( ( c + d) * e) \]

还是先画出这个表达式的二叉树结构
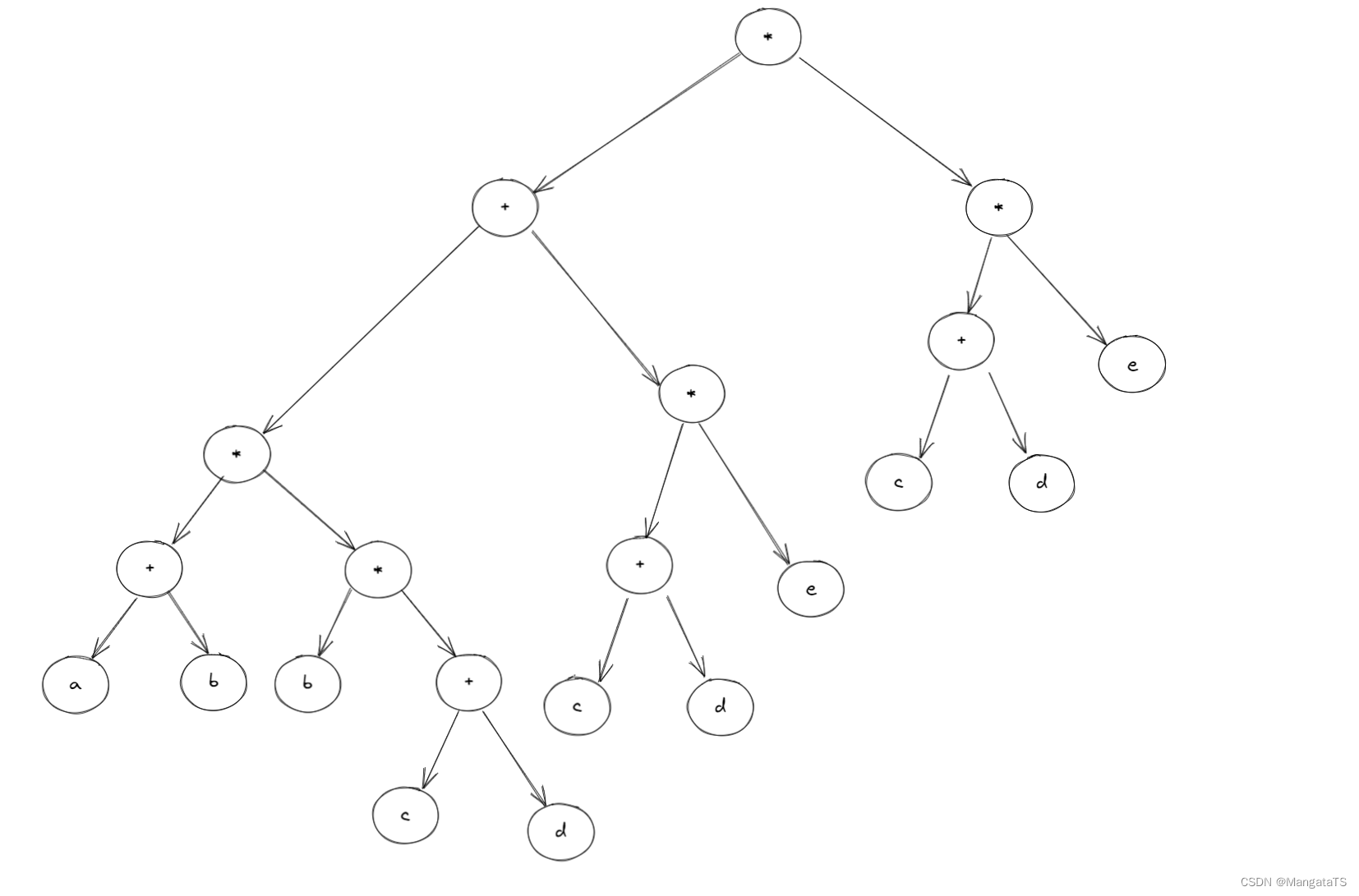
在这里插入图片描述
我们发现对于根结点的右子树 \((c+d)*e\) 其实可以删掉,，用根节点指向另一个一样的子树结点，于是得到了如下结构：

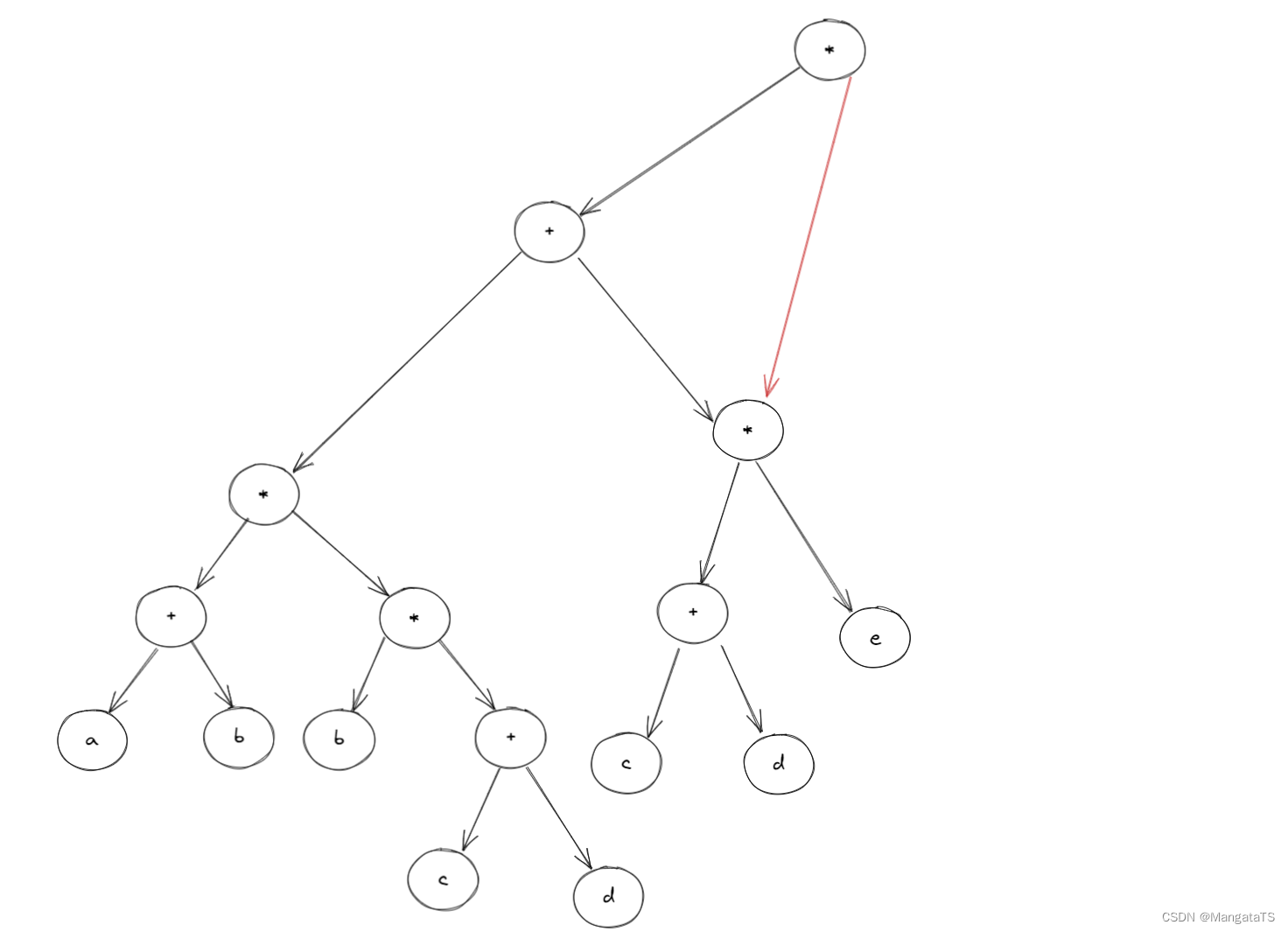
在这里插入图片描述
然后我们发现子树结构 \((c+d)\) 其实也是重复的，于是我们决定删除一个，就得到了如下结构：
在这里插入图片描述
然后我们发现结点 \(b\) 其实也是重复的，于是我们删除一个就得到了：
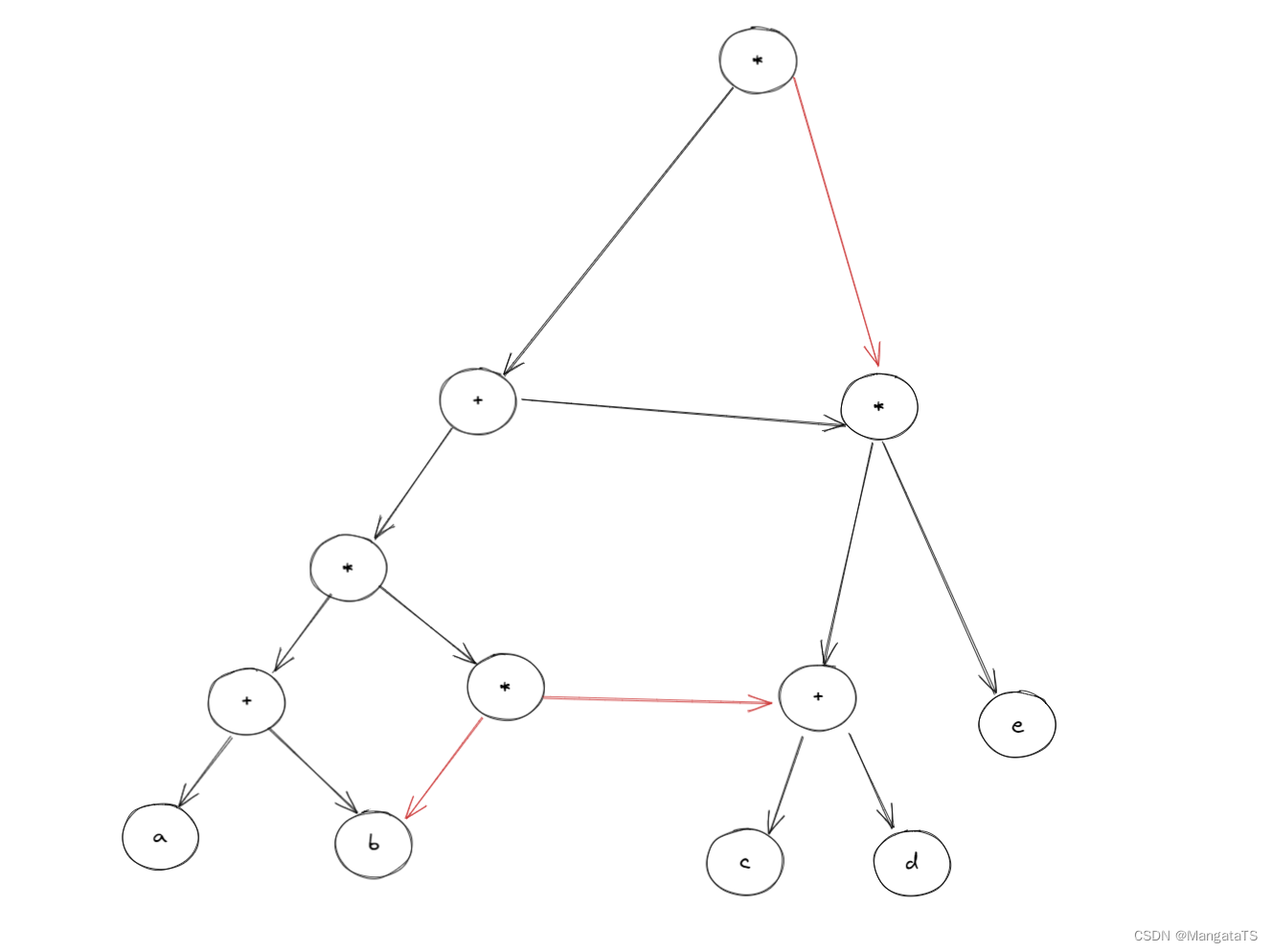
在这里插入图片描述
我们发现化二叉树为 \(DAG\) 图的时候实际上就是将二叉树重复的子树删掉，并且将分支结点指向其中一个子树即可

4.4 拓扑排序

拓扑排序算法在我另一篇博客有较为详细的讲解：
https://acmer.blog.csdn.net/article/details/126533628

4.5 关键路径

关键路径算法在我另一篇博客有较为详细的讲解：
https://acmer.blog.csdn.net/article/details/126537260

五、错题

选择题

在这里插入图片描述

若 \(E'\) 中的边对应的顶点不是 \(V'\) 的元素， \(V'\) 和 \({E'}\) 无法构成图，故选项 \(B\) 错
且若图非连通， 则从某一顶点出发无法出问到其他全部顶点，选项 \(D\) 的说法不准确

在这里插入图片描述

若无向图中本来就是连通的，那么该图有且只有一个连通分量（极大连通子图）就是其本身（若是其子集构成的新无向图则不是原图的连通分量，而是属于新图的连通分量）
若无向图不是连通的，那么其每一个连通子图都是一个连通分量

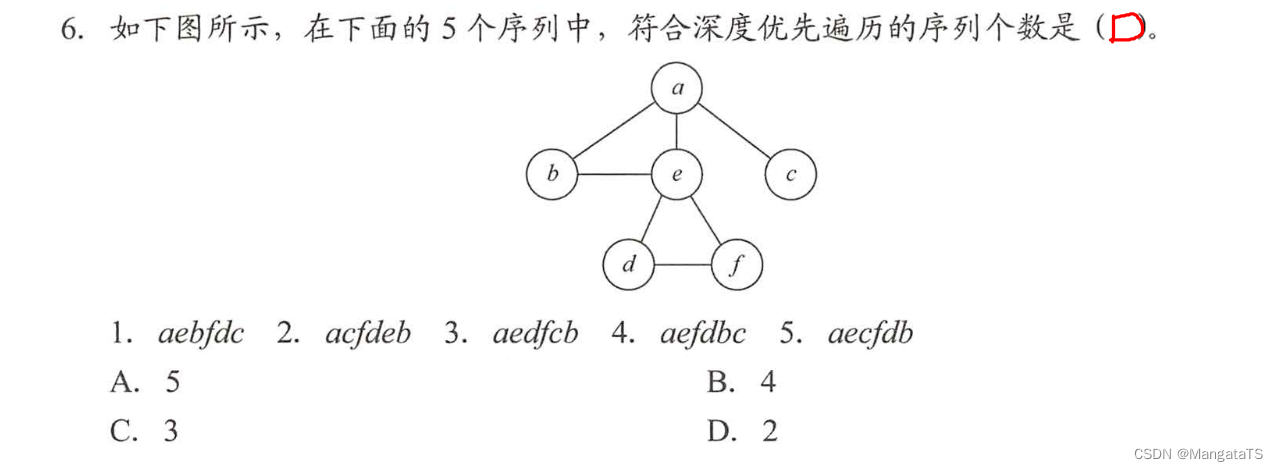
在这里插入图片描述

这里符合深度优先遍历的序列数只有第一个以及第四个，其余都不符合

判断有向图中是否存在回路，除可以利用拓扑排序外，还可以利用什么算法？ \((C)\)

  • A. 求关键路径的方法
  • B. 求最短路径的 Dijkstra 算法
  • C. 深度优先边历算法
  • D. 广度优先选历算法
    解析：利用深度优先遍历可以判断图 \(G\) 中是否存在回路。对于无向图来说，若深度优先遍历过程中遇到了回边，则必定存在环；对于有向图来说，这条回边可能是指向深度优先森林中另一棵生成树上的顶点的弧；但是，从有向图的某个顶点 \(v\) 出发进行深度优先遍历时，若在 \(DFS(v)\)结束之前 出现一条从顶点 \(u\) 到顶点 \(v\) 的回边，且 \(u\) 在生成树上是 \(v\) 的子孙，则有向图必定存在包含顶点 \(v\) 和顶点 \(u\) 的环

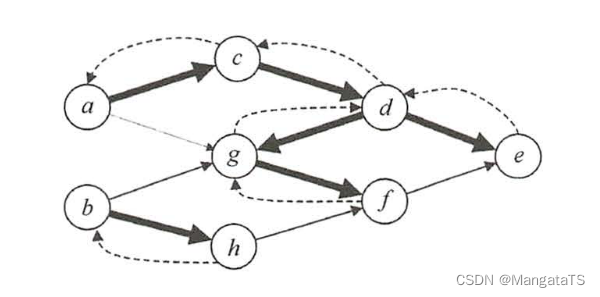
在这里插入图片描述

对一个有向图做深度优先遍历，并未专门判断有向图是否有环（有向回路〉存在，无论图中 是否有环，都得到一个顶点序列。若无环，在退出边归过程中输出的应是逆拓扑有序序列。对有向无环图利用深度优先搜索进行拓扑排序的例子如下：
如下图所示，退出 \(DFS\) 栈的顺序为 \(efgdcahb\) ，此图的一个拓扑序列为 \(bhacdgfe\) 。该方法的每一步均是先输出当前无后继的结点，即对每个结点 \(v\) ，先递归地求出 \(v\) 的每个后继的拓扑序列。 对于一个\(AOV\) 网，按此方法输出的序列是一个逆拓扑序列 。
在这里插入图片描述

在这里插入图片描述

若不存在拓扑排序，则表示圈中必定存在回路，该回路构成一个强连通分量

在这里插入图片描述

  • \(Ⅰ\) 中，对于一个存在环路的有向图，使用拓扑排序算法运行后，肯定会出现有环的子图，在此环中无法再找到入度为 \(0\) 的结点，拓扑排序也就进行不下去。
  • \(Ⅱ\) 中，注意，若两个结点之间不存在祖先或子孙关系，则它们在拓扑序列中的关系是任意的（即前后关系任意），因此使用栈和队列都可以，因为进栈或队列的都是入度为 \(0\) 的结点，此时入度为 \(0\) 的所有结点是没有关系的。
  • \(Ⅲ\) 中，若拓扑有序序列唯一，则很自然地让人联系到一个线性的有向图（错误），下图的拓扑序列也是唯一的，但度却不满足条件
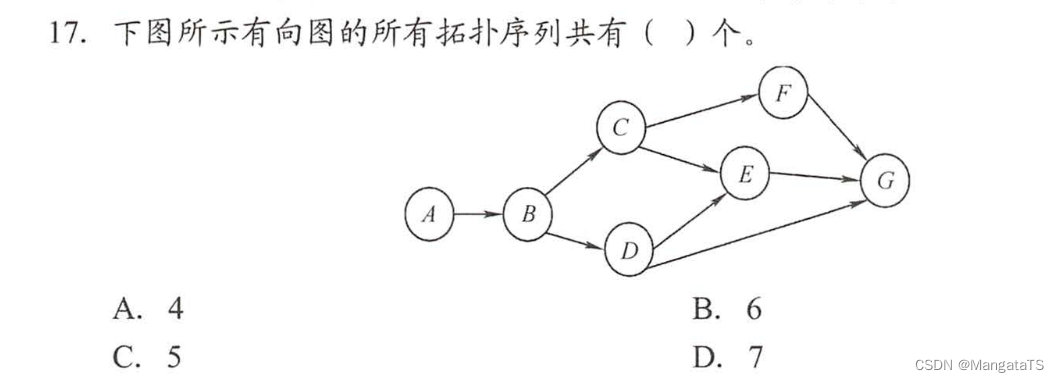
    在这里插入图片描述

在这里插入图片描述

总共有五种：

  • ABCDEFG
  • ABCDFEG
  • ABDCEEG
  • ABDCFEG
  • ABCFDEG

在这里插入图片描述

  • \(Ⅰ\) ：有向图中的度为入度加出度，而矩阵中第 \(V\) 行只能代表点 \(V\) 的出度数
  • \(Ⅱ\) ：无向图的邻接矩阵一定是对称矩阵，有向图的邻接矩阵也有可能是对称矩阵
  • \(Ⅲ\) ：最小生成树中的 \(n-1\) 条边并不能保证是图中权值最小的 \(n - 1\) 条边， 因为权值最小的 \(n-1\) 条边并不一定能使图连通，所以会存在某条边权值超过未选的边
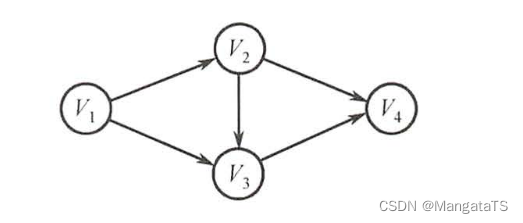
  • \(Ⅳ\) ：有向无环图的拓扑序列唯一并不能唯一确定该图。在下图所示的两个有向无环图中，拓扑序列都为\(V_1, V_2, V_3,V_4\)
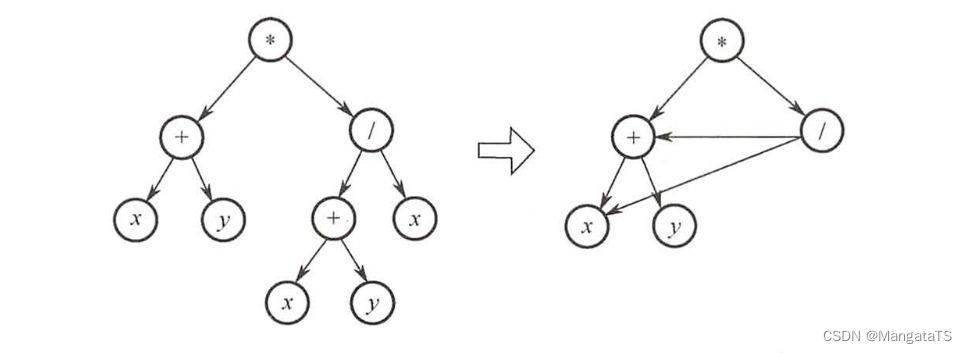
    在这里插入图片描述

在这里插入图片描述

先将该表达式转换成有向二叉树，注意到该二叉树中有些顶点是重复的，为了节省存储空间， 可以去除重复的顶点（使顶点个数达到最少），将有向二叉树去重转换成有向无环图，如下图所示。
在这里插入图片描述

标签：图论,有向图,1.2,连通,路径,结点,顶点,数据结构,考研
From： https://www.cnblogs.com/Mangata/p/16634336.html

相关文章

  • Highway - 图论 - 树的直径 - 最短路
    http://https://ac.nowcoder.com/acm/problem/52867题目大意有n个城市，城市之间有n-1条无向道路。Bob在任意两个城市之间建造高速公路的花费是这两个城市之间的最短路径......
  • 数据结构和算法的介绍
    声明：此系列以尚硅谷数据结构与算法（Java数据结构与算法）视频为主，包括其他大佬的文章（相关文中有引用注明来源）在此声明一次，后续文档中不再声明。目录数据结构和算法的关系算......
  • 模板——数据结构
    线段树维护区间最值以及满足最值的个数structSGT{ intmx[N<<2],tg[N<<2],su[N<<2]; #definemid((l+r)>>1) #definelc(u<<1) #definerc((u<<1)|1) voidbld(......
  • 21级数据结构与算法实验2——链表
    21级数据结构与算法实验2——链表28天7-1单链表的创建及遍历分数30作者陈晓梅单位广东外语外贸大学读入n值及n个整数，建立单链表并遍历输出。输入格式:读入n及......
  • 数据结构
    定义：数据结构是计算机存储、组织数据的方式。 数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。、 数据结构......
  • matlab中数据结构之-tables
    作为matlab中的一种数据结构，是一种按行和列存储信息的一种表格式的数据结构，同一列中的数据具有相同的长度，和我们平常见到的表差不多。使用关键table函数创建，格式为tabl......
  • 基础数据结构之链表相关的一些问题
    基础数据结构之链表相关的一些问题作者：Grey原文地址：博客园：基础数据结构之链表相关的一些问题CSDN：基础数据结构之链表相关的一些问题反转单链表题目描述见：LeetCode20......
  • 面试官：HashSet 的实现原理是怎样的？底层是什么数据结构？被问到了。。
    来源：https://www.cnblogs.com/LiaHon/p/11257805.html一.HashSet概述HashSet是Java集合Set的一个实现类，Set是一个接口，其实现类除HashSet之外，还有TreeSet，并继承了Collect......
  • 数据结构与算法分析--C语言描述 pdf
    高清扫描版下载链接：https://pan.baidu.com/s/1BGsOOAOqXE9j509OFtkjXA点击这里获取提取码书中详细介绍了当前流行的论题和新的变化，讨论了算法设计技巧，并在研究算法的性能......
  • 数据结构与算法分析 Java版 pdf
    高清扫描版下载链接：https://pan.baidu.com/s/1vDsOy1E0kHizahB6hIg2tA点击这里获取提取码本书以Java语言为基础，讨论了数据结构的线性结构和非线性结构及其实现，全书以Java......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99