环形队列

环形队列理论

环形队列的本质就是一个数组。用两个标识分别表示对头和队尾，在逻辑上呈现为一个环形
当队列不为空时，对头指向头元素，队尾指向最后一个元素的下一个元素

下图为空队列(队列的初始状态)

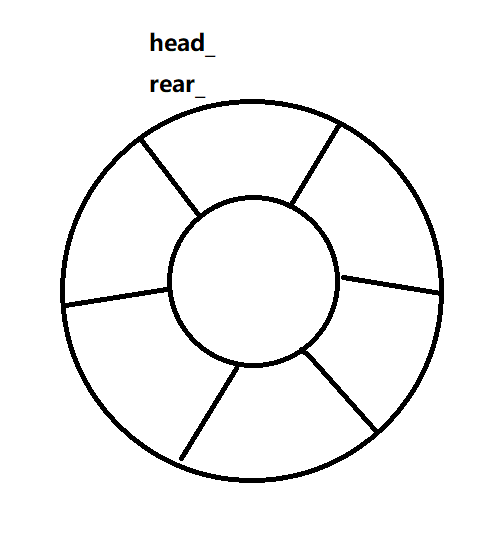
入队：从对尾入队，arr[rear_] = val; (rear_+1) % arr.length();
出队：从对头出队，(head_+1) % arr.length();

考虑到一个问题，队列空与队列满的表示都为 head_ = rear_; 这显然是错误的。为了解决这个问题，就不能将数组中的全部空间都使用(这会导致对头与队尾相遇，这与对空的判断吻合)。
而要预留一个数组元素

对满状态如图：

那么堆满的判断就变成了 (rear_+1) % arr.length() == head_

环形队列代码

#include<iostream>
using namespace std;

class Queue
{
public:
	Queue(int size = 10)
		:cap_(size)
		, front_(0)
		, rear_(0)
		, pQue_(new int[cap_])
	{
	}
	~Queue()
	{
		delete[] pQue_;
		pQue_ = nullptr;
	}
	void push(int val)
	{
		if (full())
		{
			expand(2 * cap_);
		}
			pQue_[rear_] = val;
			rear_ = (rear_ + 1) % cap_;
	}
	void pop()
	{
		if (empty()) 
			throw " queue is empty";
		else
		{
			front_ = (front_ + 1) % cap_;
		}
	}
	int front() const
	{
		if (empty()) throw "queue is empty";
		else
		{
			return pQue_[front_];
		}
	}
	int back() const
	{
		if (empty()) throw "queue is empty";
		else
		{
			return pQue_[(rear_ - 1 + cap_) % cap_];
			//为了解决访问数组末尾元素
			//当要访问最后一个元素时，rear_位于数组头
		}
	}
	int size()
	{
		int size = 0;
		for (int i = front_; i != rear_; i=((i+1)%cap_))
		{
			size++;
		}
		return size;
	}

	bool full() const
	{
		if ((rear_ + 1)%cap_ == front_)
			return true;
		else
			return false;
	}
	bool empty() const
	{
		if (rear_ == front_)
			return true;
		else
			return false;
	}

private:

	void expand(int size)
	{
		//不可以和栈、数组一样 使用memcpy，来进行内存拷贝
		int* ret = new int[size];
		int num = 0;
		for (int i = front_; i != rear_; num++,i=(i + 1) % cap_)
		{
			ret[num] = pQue_[i];
		}
		delete[] pQue_;
		pQue_ = ret;
		front_ = 0;
		rear_ = num;
		cap_ = size;
	}

	int cap_;
	int* pQue_;
	int front_;
	int rear_;
};

不能使用memcpy的原因

这使拷贝变得无意义

链式队列 (基于双向循环链表)

与链式栈相同，都是为了解决当数组内元素过多时，扩容的事件负责都为O(n)，浪费时间。若采用链式队列，就可以使扩容操作的时间复杂度将为O(1)

#include<iostream>
using namespace std;

class listQueue
{
public:
	listQueue()
	{
		head_ = new Node();
		head_->next_ = head_;
		head_->pre_ = head_;
	}
	~listQueue()
	{
		while (head_->next_ != head_)
		{
			Node* t = head_->next_;
			head_->next_ = head_->next_->next_;
			t->next_->pre_ = head_;
			delete t;
		}
		delete head_;
		head_ = nullptr;
	}
	void  push(int val)
	{
		Node* p = head_->pre_;
		Node* node = new Node(val);
		node->next_ = head_;
		node->pre_ = p;
		head_->pre_ = node;
		p->next_ = node;
	}
	void pop()
	{
		Node* p = head_->next_;
		head_->next_ = head_->next_->next_;
		p->next_->pre_ = head_;
		delete p;
	}
	int front()
	{
		if (head_->next_ != head_)
		{
			return head_->next_->data_;
		}
		else throw "is empty";
	}
	int back()
	{
		if (head_->pre_ != head_)
		{
			return head_->pre_->data_;
		}
		else throw "is empty";
	}
private:

	struct Node
	{
		Node(int data = 0)
			:data_(data)
			,pre_(nullptr)
			,next_(nullptr)
		{ }
		int data_;
		Node* pre_;
		Node* next_;
	};
	Node* head_; //指向头节点
};