斜率优化DP
例题
朴素dp
设 \(dp_i\) 表示前 \(i\) 个物品,分若干段的最小代价。
状态转移方程为:
\[dp_{i}=\min _{j<i}\left\{dp_{j}+\left(i-(j+1)+s_{i}-s_{j}-L\right)^{2}\right\}=\min _{j<i}\left\{dp_{j}+\left(s_{i}-s_{j}+i-j-1-L\right)^{2}\right\} \]其中 \(pre_i\) 表示前 \(i\) 个数的和,即 \(\sum_{j=1}^i c_j\)。
该做法时间复杂度为 \(O(n^2)\),直接爆炸。
优化
为方便表示,令 \(L'=L+1\)
我们将式子改写为如下形式:
\[\begin{align*} dp_i &= dp_j+(s_i-s_j+i-j-L')^2 \\ dp_i &= dp_j+((s_i+i-L')+(-s_j-j))^2 \\ dp_i &= dp_j+(s_i+i-L')^2+2(s_i+i-L')(-s_j-j)+(-s_j-j)^2 \\ dp_i-(s_i+i-L')^2 &= dp_j+(s_j+j)^2-2(s_i+i-L')(s_j+j) \end{align*} \]考虑一次函数式子 \(y=kx+b\),将其移项得到 \(b=y-kx\)。我们将只与 \(j\) 有关的信息表示为 \(y\),把同时与 \(i,j\) 有关的信息表示为 \(kx\)(其中与 \(i\) 相关的作 \(k\),与 \(j\) 相关的作 \(x\)),把只与 \(i\) 有关的信息(要求的信息)表示为 \(b\)。具体地,设
\[\begin{align*} b_i &= dp_i-(s_i+i-L')^2 \\ k_i &= 2(s_i+i-L') \\ y_j &= dp_j+(s_j+j)^2 \\ x_j &= s_j+j \end{align*} \]则转移方程 \(dp_i-(s_i+i-L')^2 = dp_j+(s_j+j)^2-2(s_i+i-L')(s_j+j)\) 就可以写作
\[b_i=\min_{j<i}\{y_j-k_ix_j\} \]我们把 \((x_j,y_j)\) 看作二维平面上的点,则 \(k_i\) 表示直线斜率, \(b_i\) 表示一条经过 \((x_j,y_j)\) 的斜率[1]为 \(k_i\) 的直线的截距。问题转化为了:选择合适的 \(j \ (1 \le j < i)\),最小化直线的截距(即 \(b_i\))。
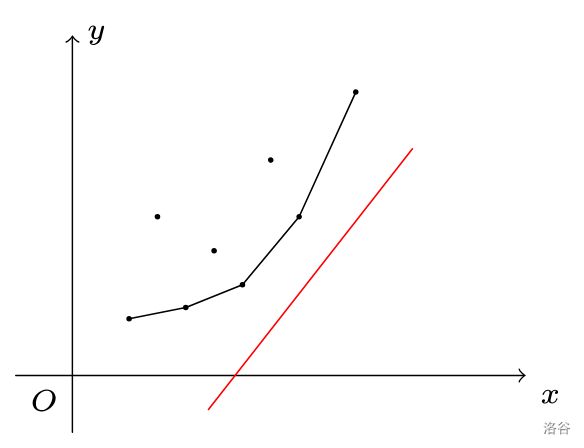
如图,我们将这个斜率为 \(k_i\) 的直线从下往上平移,直到有一个点 \((x_p,y_p)\) 在这条直线上,则有 \(b_i=y_p-k_ix_p\),这时 \(b_i\) 取到最小值。算完 \(f_i\),我们就把这个点 \((x_i,y_i)\) 这个点加入点集中,以做为新的 dp 决策。那么,我们该如何维护点集?
容易发现,可能让 \(b_i\) 取到最小值的点一定在凸壳上。因此在寻找 \(p\) 的时候我们就不需要枚举所有 \(i-1\) 个点,只需要考虑凸包上的点。在本题中 \(k_i\) 随着 \(i\) 的增加而增加,因此我们可以单调队列维护凸包。
具体地,设 \(K(a,b)\) 表示过 \((x_a,y_a)\) 和 \((x_b,y_b)\) 的直线的斜率。考虑单调队列 \(q_l,q_{l+1},\dots,q_r\),维护的时下凸包上的点。也就是说,对于 \(l<i<r\),始终有 \(K(q_{i-1},q_i)<K(q_i,q_{i+1})\) 成立。
我们维护一个指针 \(e\) 来计算 \(b_i\) 的最小值。我们需要找到一个 \(K(q_{e-1},q_e)\le k_i <K(q_e,q_{e+1})\) 的 \(e\),这时就有 \(p=q_e\),即 \(q_e\) 是 \(i\) 的最优决策点。
在插入一个点 \((x_i,y_i)\) 时,我们要判断是否 \(K(q_{r-1},q_r)<K(q_r,i)\),如果不等式不成立就将 \(q_r\) 弹出,直到等式满足。然后将 \(i\) 插到 \(q\) 队尾。
代码实现
- 初始状态入队
- 每次使用一条和 \(i\) 相关的直线 \(f(i)\) 去切维护的凸包,找到最优决策,更新 \(dp_i\)。
- 加入状态 \(dp_i\)。如果一个状态(即凸包上的一个点)在 \(dp_i\) 加入后不再是凸包上的点,需要在 \(dp_i\) 加入前将其剔除。
时间复杂度 \(O(n)\)。
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int INF = 0x3f3f3f3f;
const int N = 5e4 + 10;
int n, L;
int c[N], s[N];
int dp[N], q[N], head = 1, tail = 0;
int b(int i) {return dp[i] - (s[i] + i - L - 1) * (s[i] + i - L - 1); } // 定义 b
int k(int i) {return 2 * (s[i] + i - L - 1); } // 定义 k
int y(int j) {return dp[j] + (s[j] + j) * (s[j] + j); } // 定义 y
int x(int j) {return s[j] + j; } // 定义 x
double slope(int i, int j) { // 定义 K(a, b)
return 1.0 * (y(i) - y(j)) / (x(i) - x(j));
}
signed main() {
scanf("%lld%lld", &n, &L);
for (int i = 1; i <= n; i++) {
scanf("%lld", &c[i]);
s[i] = s[i - 1] + c[i];
}
memset(dp, INF, sizeof(dp));
dp[0] = 0;
q[++tail] = 0;
for (int i = 1; i <= n; i++) {
while (head < tail && slope(q[head], q[head + 1]) < k(i)) { // 改点不可能是最优决策点,出队
head++;
}
dp[i] = y(q[head]) - k(i) * x(q[head]) + (s[i] + i - L - 1) * (s[i] + i - L - 1);
while (head < tail && slope(q[tail - 1], q[tail]) > slope(q[tail], i)) { // 若该点不再是凸壳上的点,则将其踢出队列
tail--;
}
q[++tail] = i;
}
printf("%lld\n", dp[n]);
return 0;
}
小结
具体的代码实现因题就题,比较抽象,要考虑是上凸包还是下凸包,事踢对头还是踢队尾之类的。注意上凸包斜率越来越小,下凸包斜率越来越大。
CDQ优化
一般用不上,但是放在这里。
对于有些问题,斜率并不是单调的。这时我们需要维护凸包上的每一个节点,然后每次用当前的直线去切这个凸包。
本题与「玩具装箱」问题唯一的区别是,玩具的价值可以为负。延续之前的思路,设 \(dp_i\) 表示前 \(i\) 个物品,分若干段的最小代价。
状态转移方程为:
\[dp_{i}=\min _{j<i}\left\{dp_{j}+\left(s_{i}-s_{j}+i-j-1-L\right)^{2}\right\} \]其中 \(pre_i\) 表示前 \(i\) 个数的和,即 \(\sum_{j=1}^i c_j\)。
将方程做相同的变换:
\[dp_i-(s_i+i-L')^2 = \min_{j<i}\{dp_j+(s_j+j)^2-2(s_i+i-L')(s_j+j)\} \]然而这时有两个条件不成立了:
- 直线的斜率不再单调;
- 每次加入的决策点的横坐标不再单调。
仍然考虑凸壳的维护。
在寻找最优决策点,也就是用直线切凸壳的时候,我们将单调队列找队首改为:凸壳上二分。我们二分出斜率最接近直线斜率的那条凸壳边,就可以找到最优决策。
在加入决策点,也就是凸壳上加一个点的时候,我们有两种方法维护。
第一种方法是直接用平衡树维护凸壳。那么寻找决策点的二分操作就转化为在平衡树上二分,插入决策点就转化为在平衡树上插入一个结点,并删除若干个被踢出凸壳的点。此方法思路简洁但实现繁琐。
来说一种基于 CDQ 分治的做法。
设 \(CDQ(l, r)\) 表示计算 \(f_i,i\in[l,r]\)。考虑 \(CDQ(1,N)\):
- 我们先调用 \(CDQ(1,mid)\) 算出 \(f_i,i\in[1,mid]\)。然后我们对 \([1,mid]\) 这个区间内的决策点建凸包,然后用这个凸包去更新 \(f_i,i\in[mid+1,n]\)。这时我们决策点集是固定的,不像之前那样边计算 DP 值边加入决策点,那么我们就可以把 \(i\in[mid+1,n]\) 的 \(f_i\) 先按照直线的斜率 \(k_i\) 排序,然后就可以使用单调队列来计算 DP 值了。
- 对于 \([mid+1,n]\) 中的每个点,如果它的最优决策的位置是在 \([1,mid]\) 这个区间,在这一步操作中他就会被更新成最优答案。当执行完这一步操作时,我们发现 \([1,mid]\) 中的所有点已经发挥了全部的作用,凸壳中他们存不存在已经不影响之后的答案更新。因此我们可以直接舍弃这个区间的决策点,并使用 \(CDQ(mid+1,n)\) 解决右区间剩下的问题。
时间复杂度 \(O(n\log^2n)\)。
小结
对比「玩具装箱」和「玩具装箱 改」,可以总结出以下两点:
- 二分/CDQ/平衡树等能够优化 DP 方程的计算,于一定程度上降低复杂度,但不能改变这个方程本身。
- DP 方程的性质会取决于数据的特征,但 DP 方程本身取决于题目中的数学模型。
一个点 \((x,y)\) 的斜率为 \(\frac{y}{x}\)。 ↩︎
