在现代技术领域算法决策优化已成为核心竞争力。Meta通过广告位置优化提升点击率,Netflix利用缩略图优化提升用户参与度,亚马逊依靠产品推荐系统提升销售额——这些优化的背后都采用了基于Beta分布的汤普森采样算法。
在各类决策系统中,探索与利用的平衡是一个根本性挑战。例如推荐系统是继续使用已验证有效的选项,还是尝试潜在更优的新选项?汤普森采样通过Beta分布提供了解决这一难题的数学框架。
贝叶斯推理基础
在深入Beta分布和汤普森采样之前,需要先理解贝叶斯推理的核心概念。
贝叶斯推理是一种统计推理方法,其核心是运用贝叶斯定理来根据新的观测数据不断更新假设的概率分布。
贝叶斯定理的基本形式为:
后验概率 ∝ 似然度 × 先验概率
其中:
- 先验概率:表示在获取新数据前对参数的初始概率估计
- 似然度:代表在给定参数条件下观测到当前数据的概率
- 后验概率:结合新数据后对参数的更新估计
共轭先验分布
在贝叶斯统计中,如果后验分布与先验分布属于同一分布族,则称该先验分布为似然函数的共轭先验。这一性质使得概率更新的计算大为简化。
Beta分布是二项分布和伯努利分布的共轭先验。当先验采用Beta分布,似然函数为二项分布或伯努利分布时,后验分布仍然是Beta分布。这种共轭性质使得在线学习过程中的概率更新变得高效可行。
Beta分布的数学基础
Beta分布是定义在[0,1]区间上的连续概率分布,特别适合对概率和比例进行建模。
核心参数
Beta分布由两个形状参数控制:
- α (alpha):可理解为观测到的成功次数加1
- β (beta):可理解为观测到的失败次数加1
这两个参数决定了分布的形状特征:
- α值增大会使分布向1偏移,表示成功概率增加
- β值增大会使分布向0偏移,表示失败概率增加
分布特征
Beta分布的形状由α和β的相对大小决定:
- α > β:分布偏向1,表示成功概率较高
- β > α:分布偏向0,表示失败概率较高
- α = β:分布关于0.5对称
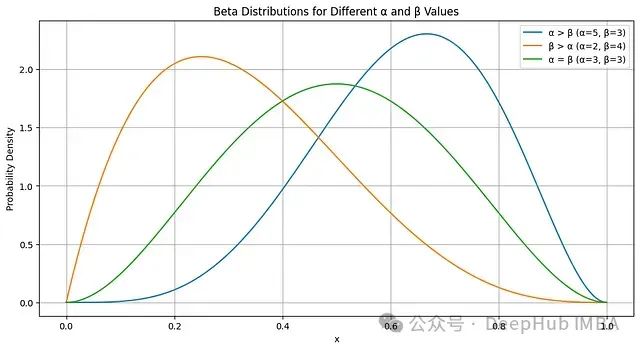
概率密度函数
Beta分布的PDF虽然涉及复杂的伽玛函数,但其形状完全由α和β两个参数决定,这使得它在实际应用中便于操作和理解。
https://avoid.overfit.cn/post/9423af7a03534afea00f84416e926d0d
标签:采样,概率,汤普森,贝叶斯,Beta,分布,先验 From: https://www.cnblogs.com/deephub/p/18594304