第一个题单编辑到后面实在是太卡了,就新开了一个,以后应该也会 \(30\) 题为一个题单。
31.CF1580D Subsequence
不会笛卡尔树,但是看到题解区的妙妙解法......
题目的式子非常大便,我们考虑把它翻译成人话:
一个子序列的价值为: \(sum*m - 每两个数及他们之间的所有数的\min\)。
设 \(f[l][r][k]\) 表示在 \([l,r]\) 中选出 \(k\) 个数的最大代价(为了方便我们前面那一项不 \(\times k\),而是还是\(\times m\))。
假设 \([l,r]\) 的最小值位置是 \(pos\),如果最后选出的数不跨越 \(pos\),可以递归分治。
现在考虑跨越 \(pos\) 的情况,我们有两个转移:
- \(f[l][pos-1][i]+f[pos+1][r][j] - 2 \times i \times j \times a[pos] \to f[l][r][i+j]\)
- \(f[l][pos-1][i]+f[pos+1][r][j] + m\times a[pos] - [2\times (i+1) \times (j+1)-1] \times a[pos] \to f[l][r][i+j+1]\)
我们来解释一下:
- 不选择 \(a[pos]\),那么左端点在 \(a[pos]\) 左边,右端点在 \(a[pos]\) 右边的贡献就是 \(-2\times i\times j\times a[pos]\) (\(\times 2\)是因为每一对会贡献两次,因为题目中的 \(j\) 是从 \(1\) 开始,而不是 \(i\))
- 选择 \(a[pos]\),那么左端点 \(pos\) 或在 \(a[pos]\) 左边,右端点 \(=pos\) 或在 \(a[pos]\) 右边的贡献是 \(-[2\times (i+1)\times (j+1)-1]\times a[pos]\) ,\(-1\) 是因为当计算题目中的 \(f\) 时左右端点都在 \(pos\) 时只能贡献一次
递归分治求解,时间复杂度可以近似认为是:
\(T(n)=2 \times T(\frac{n}{2})+O(n^2)\)
根据主定理他等于 \(O(n^2)\)
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,m,a[N];
vector<int> work(int l,int r){
vector<int> f(r-l+2,LLONG_MIN);
f[0]=0;
if(l>r) return f;
int pos=l;
for(int i=l+1;i<=r;i++) if(a[pos]>a[i]) pos=i;
vector<int> fl=work(l,pos-1),fr=work(pos+1,r);
for(int i=0;i<fl.size();i++){
for(int j=0;j<fr.size();j++){
f[i+j]=max(f[i+j],fl[i]+fr[j]-2*i*j*a[pos]);
f[i+j+1]=max(f[i+j+1],fl[i]+fr[j]+m*a[pos]-(2*(i+1)*(j+1)-1)*a[pos]);
}
}
return f;
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=read();
printf("%lld\n",work(1,n)[m]);
return 0;
}
32.P1220 关路灯
经典套路之——费用提前计算。
如果设 \(f[l][r][0/1]\) 表示关掉区间 \([l,r]\) 内的路灯后,且最后停在 \(l/r\),区间 \([l,r]\) 的路灯的最小花费。
不难想到是从 \(f[l+1][r]\) 和 \(f[l][r-1]\) 转移过来。
但是转移时我们无法知道从开始到现在经过的时间,也就无法知道新加进来的路灯到底消耗了多少。
设 \(f[l][r][0/1]\) 表示关掉区间 \([l,r]\) 内的路灯后,且最后停在 \(l/r\),所有路灯的最小花费。
以从 \(f[l+1][r][0]\) 转移到 \(f[l][r][0]\) 为例,在转移时,我们不用再考虑在关 \([l+1,r]\) 内的路灯时的其他路灯的消耗。
只需要加上从 \(l+1\) 走到 \(l\) 这段时间里,\([1,l]\) 和 \([r+1,n]\) 路灯的功率消耗。
前缀和优化一下即可,转移显然。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,c,a[55],w[55],f[55][55][2];
int pre[55];
int calc(int l,int r){
return pre[r]-pre[l-1];
}
signed main(){
n=read(),c=read();
for(int i=1;i<=n;i++){
a[i]=read(),w[i]=read();
pre[i]=pre[i-1]+w[i];
}
memset(f,0x3f,sizeof f);
for(int len=1;len<=n;len++){
for(int l=1;l+len-1<=n;l++){
int r=l+len-1;
if(c<l||c>r) continue;
if(len==1) f[l][r][0]=f[l][r][1]=0;
else{
f[l][r][0]=min( f[l+1][r][0] + (a[l+1]-a[l])*(pre[n]-calc(l+1,r)) , f[l+1][r][1] + (a[r]-a[l])*(pre[n]-calc(l+1,r)) );
f[l][r][1]=min( f[l][r-1][1] + (a[r]-a[r-1])*(pre[n]-calc(l,r-1)) , f[l][r-1][0] + (a[r]-a[l])*(pre[n]-calc(l,r-1)) );
}
}
}
printf("%d\n",min(f[1][n][0],f[1][n][1]));
return 0;
}
33.抢鲜草
和上题几乎一模一样。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e3+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,x,a[N];
int f[N][N][2];
/*
考虑贡献提前计算
f[l][r][0/1]: 表示kona采集完所有的 [l,r] 中的草,最后在 i/j 时,所有草的最小损失青草量
(注意"所有")
*/
signed main(){
n=read(),x=read();
for(int i=1;i<=n;i++) a[i]=read();
sort(a+1,a+n+1);
memset(f,0x3f,sizeof f);
for(int len=1;len<=n;len++){
for(int l=1;l+len-1<=n;l++){
int r=l+len-1;
if(l==r){
f[l][r][0]=f[l][r][1]=abs(a[l]-x)*n;
}
else{
// f[l][r][0]=min(f[l+1][r][0] + (a[l+1]-a[l]) * (n-(r-(l+1)+1)),f[l+1][r][1] + (a[r]-a[l]) * (n-(r-(l+1)+1)) ); //最原始的式子方便理解
f[l][r][0]=min(f[l+1][r][0] + (a[l+1]-a[l]) * (n-r+l),f[l+1][r][1] + (a[r]-a[l]) * (n-r+l));
f[l][r][1]=min(f[l][r-1][1] + (a[r]-a[r-1]) * (n-r+l),f[l][r-1][0] + (a[r]-a[l]) * (n-r+l));
}
}
}
printf("%lld\n",min(f[1][n][0],f[1][n][1]));
return 0;
}
34.P4161 [SCOI2009] 游戏
如果把它根据对应关系连边会得到若干环,假设第 \(i\) 个环的环长为 \(len[i]\)。那么这个环里的数要恢复原样就要 \(len[i]\) 步。进一步的,容易得出整个序列要恢复原样需要 \(lcm(len[1],len[2],...)\)。
问题转化为:给你一个 \(n\) , 构造若干个数,使得他们的和为 \(n\), 求他们的 \(lcm\) 的可能的情况数。
怎么构造出尽可能多的 \(lcm\)?
如果每一次这若干个数都互质,那他们的 \(lcm = 他们的乘积\),从而每一次都不一样。
具体的,我们只需要让每个数都形如 \(pi^{ki}\) (\(pi\)是质数,\(ki\)是非负整数) , 那根据算数基本定理,只要方案不同,他们的乘积(\(lcm\))就不同。
小小的证明:如果有一个构造方案,里面的数不互质,我们完全可以把它们转换成形如上述的数列(每个质因子只保留对应的一个数),并且 \(lcm\) 不变,而且他们的总和会变小,我们只需要再往里面塞 \(1\) ,就可以了。
即任意一个情况都可以转化成上述构造方法。
设 \(f[i][j]\) 表示用前 \(i\) 个质数,凑出和为 \(j\) 的方案数,\(f[i][j]=f[i-1][j-(prime_i)^k]\),因为可以往里面塞好多个 \(1\) , 所以我们钦定 \(k>0\);因为 \(i\) 可以不选,所以 \(f[i][j]+=f[i-1][j]\)。
初始化 \(f[0][0]=1\)。
最后的答案是 \(\sum_{j=0}^{n} f[max_i][j]\) (\(max_i\) 是最大的不超过 \(n\) 的质数) 。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e3+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n;
bool stater[N];
int cnt,pri[N];
void Eular(int n){
stater[1]=1;
for(int i=2;i<=n;i++){
if(!stater[i]) pri[++cnt]=i;
for(int j=1;j<=cnt&&i*pri[j]<=n;j++){
stater[i*pri[j]]=true;
if(i%pri[j]==0) break;
}
}
}
int f[N][N];
signed main(){
n=read();
Eular(n);
f[0][0]=1;
for(int i=1;i<=cnt;i++){
for(int j=0;j<=n;j++){
f[i][j]=f[i-1][j];
for(int k=pri[i];k<=j;k*=pri[i]) f[i][j]+=f[i-1][j-k];
}
}
int ans=0;
for(int j=0;j<=n;j++) ans+=f[cnt][j];
printf("%lld\n",ans);
return 0;
}
35.P6280 [USACO20OPEN] Exercise G
P6280 [USACO20OPEN] Exercise G
这题和上一题基本上是一样的。
- 一样的图论连边得出每个排列需要的步数为\(lcm(len[i])\)。
- 一样的分析过程:我们只需要让每个数都形如 \(pi^{ki}\) (\(pi\)是质数,\(ki\)是非负整数)。
- 基本一样的DP状态:
\(f[i][j]\) 表示用前 \(i\) 个质数,凑出和为 \(j\) 的所有 \(lcm\) 的和。 - 基本一样的转移:\(f[i][j]=f[i-1][j-(prime_i)^k]*(prime_i)^k\) (因为互素,所以直接乘以 \(i^k\) 就是新的 \(lcm\))。
- 唯一不一样的:\(N=1e4\),所以滚动数组。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e4+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,mod;
bool stater[N];
int cnt,pri[N];
void Eular(int n){
stater[1]=1;
for(int i=2;i<=n;i++){
if(!stater[i]) pri[++cnt]=i;
for(int j=1;j<=cnt&&i*pri[j]<=n;j++){
stater[i*pri[j]]=true;
if(i%pri[j]==0) break;
}
}
}
int f[N];
signed main(){
n=read(),mod=read();
Eular(n);
f[0]=1;
for(int i=1;i<=cnt;i++){
for(int j=n;j>=0;j--){
for(int k=pri[i];k<=j;k*=pri[i]) (f[j]+=f[j-k]*k%mod)%=mod;
}
}
int ans=0;
for(int j=0;j<=n;j++) (ans+=f[j])%=mod;
printf("%lld\n",ans);
return 0;
}
36.P6280 [USACO20OPEN] Exercise G
P6280 [USACO20OPEN] Exercise G
一个数的二进制表示可以看成是一个集合。
设 \(dp[i]\) 表示选出若干个互不相交的集合使他们的并为 \(i\) 的方案数,则答案是 \(\sum dp[i] \times \phi(i+1)\)。因为互不相交,所以他们的和也就等于他们的并等于 \(i\)。
我们先认为原序列没有 \(0\)。
\(dp[i]=∑dp[i \oplus j]*cnt[j]\) (\(j\) 是 \(i\) 的子集,\(cnt[j]\) 表示原序列 \(j\) 出现的次数)。为了避免重复计算,当 \(j < i \oplus j\) (补集) 时就退出。
对于有 \(0\) 的情况,我们往里面可以塞任意多个 \(0\) , 所以最后 \(dp[i]=dp[i] \times 2^{cnt[0]}\)。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int M=1e6+5,N=(1<<18)+5,mod=1e9+7;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,a[M];
int pri[N],tot;
bool stater[N];
int mn[N],mx[N],k[N],phi[N];
/*
mn[i]:i的最小质因子
mx[i]:i中所含 mn[i] 的最大幂
k[i]:i中所含 mn[i] 的个数,mx[i]=mn[i]^k[i]
phi[i]:i的欧拉函数
*/
void Eular()
{
stater[1]=1;
phi[1]=1;
for(int i=2;i<N;i++)
{
if(!stater[i]) pri[++tot]=i,mn[i]=i,mx[i]=i,k[i]=1,phi[i]=i-1;
for(int j=1;j<=tot&&i*pri[j]<N;j++)
{
int x=i*pri[j];
stater[x]=true;
mn[x]=pri[j];
if(i%pri[j]==0)
{
mx[x]=mx[i]*pri[j];
k[x]=k[i]+1;
if(x!=mx[x]) phi[x]=phi[x/mx[x]]*phi[mx[x]];
else phi[x]=x/mn[x] * (mn[x]-1);
/*
phi(p^k) = p^k - p^(k-1)
= p^(k-1) * (p-1)
*/
break;
}
else
{
mx[x]=pri[j];
k[x]=1;
phi[x]=phi[i]*phi[pri[j]];
}
}
}
}
int quick_power(int a,int b){
int ans=1;
while(b){
if(b&1) (ans*=a)%=mod;
(a*=a)%=mod,b>>=1;
}
return ans;
}
int Max(int m,int x){
for(int i=x;i;i-=(i&-i)){
m=max(m,(int)log2(i&-i));
}
return m;
}
int cnt[M],f[M];
signed main(){
Eular();
n=read();
int m=0;
for(int i=1;i<=n;i++) a[i]=read(),m=Max(m,a[i]),cnt[a[i]]++;
m++;
f[0]=1;
for(int i=1;i<(1<<m);i++){
for(int s=i;s>=(i^s);s=(s-1)&i){
(f[i]+=f[i^s]*cnt[s]%mod)%=mod;
}
}
int ans=0;
for(int i=0;i<(1<<m);i++) (f[i]*=quick_power(2,cnt[0]))%=mod;
for(int i=0;i<(1<<m);i++) (ans+=f[i]*phi[i+1]%mod)%=mod;
printf("%lld\n",ans);
return 0;
}
37.CF1280D Miss Punyverse
考虑树形DP。
把每个点的点权 \(a[i]\) 设为 \(w[i]-b[i]\),
这样只要看 \(a\) 之和是否 \(>0\)。
\(f[u][i]\) 表示 \(u\) 这棵子树,分成 \(i\) 个连通块,不算包含 \(u\) 的那一块,最大的 \(>0\) 的连通块数,这样不是很转移的动,因为在合并时我们需要知道包含 \(u\) 的那一块的权值之和。
考虑贪心,我们会发现有两种比较理想的情况:
- 不算包含 \(u\) 的那一块,其余块中满足条件的块记为 \(cnt\),\(cnt\) 尽可能大。
- 包含 \(u\) 的那一块,目前的权值记为 \(val\),\(val\) 尽可能大。
事实上,肯定是按照第一种情况贪心更优,因为第二种情况里,\(u\) 的那一块权值再大也不过带来 \(1\) 的贡献,无法弥补第一种情况带来的贡献差。
用pair来存储两种情况,\(f[u][i].fi=cnt, f[u][i].se=val\)。
我们只需要首先让 \(cnt\) 尽可能大,其次才是让 \(val\) 尽可能大。
边界显然是 \(f[u][1]={0,a[u]}\)。
每次新加入一个子节点 \(v\), 我们有转移:
- 包含 v 的那一块单独成一个连通块: \(f[u][i+j].fi=f[v][j].fi+f[u][i].fi+(f[v][j].se > 0),f[u][i+j].se=f[u][i].se\)。
转移时要优先按照第一维取max(pair自己内部就是这样取max的,不用特殊处理) 。 - 包含 \(v\) 的那一块合进包含 \(u\) 的那一块: \(f[u][i+j-1].fi=f[v][j].fi + f[u][i].fi ,f[u][i+j-1].se=f[v][j].se + f[u][i].se\)。
为了防止转移时用的 f 数组被更新过了,可以开一个辅助数组暂存,也可以倒序枚举。
这个问题其实就是树形背包,但是由于这是动态规划题单系列第一道树形背包题,所以简要讲一下:
对于一个状态 \(f[u][i]\) 相当于有一个容积为 \(i\) 的背包,每一个子节点 \(v\) 对应着一组物品,第 \(j\) 个物品大小为 \(j\),价值为 \(f[v][j]\),每组物品只能选一个(因为只能选一个转移),使得在不超过背包总体积的情况下(当然这道题因为转移有点特殊其实不一定背包体积是 \(i\)),价值的和(这道题里不是简单相加)最大,即分组背包问题。
对于复杂度的分析虽然看起来有点像是 \(O(n^3)\),
但注意到一次转移我们其实可以认为是枚举了任意两个子树的大小,也可以认为是分别枚举了两棵子树内的点,一个点对最多只会在 \(lca\) 处产生一个复杂度的贡献,一共有 \(n^2\) 个点对,所以复杂度为 \(O(n^2)\)。
code
#include<bits/stdc++.h>
typedef long long ll;
#define PII pair<int,ll>
#define fi first
#define se second
using namespace std;
const int N=3e3+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int T;
int n,m;
ll a[N];
int tot,head[N],to[N<<1],Next[N<<1];
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
int Size[N];
PII f[N][N],tmp[N];
void dfs(int u,int fa){
Size[u]=1;
for(int i=0;i<=n;i++) f[u][i]={INT_MIN,INT_MIN};
f[u][1]={0,a[u]};
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa) continue;
dfs(v,u);
for(int j=1;j<=Size[u]+Size[v];j++) tmp[j]={INT_MIN,INT_MIN};
for(int j=1;j<=min(m,Size[u]);j++){ //不要用填表法,会 TLE
for(int k=1;k<=min(m,Size[v]);k++){
tmp[j+k]=max(tmp[j+k],{f[v][k].fi+f[u][j].fi+(f[v][k].se>0),f[u][j].se});
tmp[j+k-1]=max(tmp[j+k-1],{f[v][k].fi+f[u][j].fi,f[v][k].se+f[u][j].se});
}
}
for(int j=1;j<=Size[u]+Size[v];j++) f[u][j]=tmp[j];
Size[u]+=Size[v];
}
// cout<<u<<':'<<'\n';
// for(int i=1;i<=Size[u];i++){
// cout<<i<<':'<<f[u][i].fi<<','<<f[u][i].se<<'\n';
// }
}
void Init(){
tot=0;;
for(int i=1;i<=n;i++) head[i]=0,a[i]=0;
}
signed main(){
T=read();
while(T--){
n=read(),m=read();
Init();
for(int i=1;i<=n;i++){
ll b=read();
a[i]-=b;
}
for(int i=1;i<=n;i++){
ll w=read();
a[i]+=w;
}
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v),add(v,u);
}
dfs(1,0);
printf("%d\n",f[1][m].fi+(f[1][m].se>0));
}
return 0;
}
38.CF1500D Tiles for Bathroom
注意到答案是单调的,一个大正方形里的小正方形都满足
为了避免重复,我们对每个右下角统计答案。
考虑计算出 \(f[i][j]\) 表示以 \((i,j)\) 为右下角,最大的合法正方形。
考虑从 \(f[i-1][j-1]\) 的继承过来,同时会新增第 \(i\) 行和第 \(j\) 列的贡献。
因为 \(q\) 很小,我们完全可以记录对应的合法正方行里,每个颜色出现的最远的位置(这个距离定义为切比雪夫距离,即 \(\max(xi-xj,yi-yj)\) )。
所以为了方便更新,我们维护三个队列:
- \(left[i][j]\): \((i,j)\)左边前 \(q+1\) 个颜色的位置(同一种颜色取切比雪夫距离最小的,下同)
- \(up[i][j]\): \((i,j)\)上边前 \(q+1\) 个颜色的位置
- \(lu[i][j]\): \((i,j)\)左上方(即\(1 \le x \le i,1 \le y \le j\))所有的元素中,前 \(q+1\) 个颜色的位置。
\(left\) 和 \(up\) 的更新很容易,只需要加进来 \((i,j)\) 即可。
看一下 \(lu[i][j]\):只需要从 \(left[i][j-1]\),\(up[i-1][j]\),\(lu[i-1][j-1]\),\((i,j)\) 中不断取最小的即可,
维护时要满足三个队列内的元素与 \((i,j)\) 的切比雪夫距离始终单调递增。
计算 \(f[i][j]\) 时,如果 \(lu[i][j]\) 的个数不超过 \(q\),那就是 \(f[i][j]=min(i,j)\)。
否则 \(f[i][j]\) 为 \(lu[i][j]\) 的第 \(q+1\) 个颜色与 \((i,j)\) 的切比雪夫距离 \(-1\)。
时间复杂度:\(O(n^2 \times q)\)。
注意到这题卡空间,所以存位置的时候不要用 \(pair\) , 把它变成一个数。
代码有点丑。
code
#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1505;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,q,a[N][N];
int ans[N];
int PairToNum(PII u){ //把坐标 (x,y) 变成数字
return (u.fi-1)*n+(u.se-1);
}
PII NumToPair(int pos){ //把数字 变成 坐标
return {pos/n+1,pos%n+1};
}
struct Queue{
int q[12];
int head=0,tail=-1;
bool empty(){return tail<head;}
void push(PII x){
q[++tail]=PairToNum(x);
}
void pop(){
++head;
}
void pop_back(){
--tail;
}
PII front(){
if(empty()) return {0,0};
return NumToPair(q[head]);
}
int size(){return tail-head+1;};
}L[N][N],U[N][N],LU[N][N];
int calc(PII u,PII v){ //计算切比雪夫距离(真正的是不用+1的,这里要计算正方形边长所以加一))
return max(abs(u.fi-v.fi),abs(u.se-v.se))+1;
}
bool flag[N*N];
signed main(){
n=read(),q=read();
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
a[i][j]=read();
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
L[i][j].push({i,j});
for(int k=L[i][j-1].head;k<=L[i][j-1].tail;k++){
PII u=NumToPair(L[i][j-1].q[k]);
if(a[u.fi][u.se]==a[i][j]) continue;;
L[i][j].push(u);
}
if(L[i][j].size()>q+1) L[i][j].pop_back();
U[i][j].push({i,j});
for(int k=U[i-1][j].head;k<=U[i-1][j].tail;k++){
PII u=NumToPair(U[i-1][j].q[k]);
if(a[u.fi][u.se]==a[i][j]) continue;;
U[i][j].push(u);
}
if(U[i][j].size()>q+1) U[i][j].pop_back();
LU[i][j].push({i,j});
flag[a[i][j]]=true; //记录这种颜色是否出现过
int t1=L[i][j-1].head,t2=U[i-1][j].head,t3=LU[i-1][j-1].head;
while(LU[i][j].size()<=q && (!L[i][j-1].empty() || !U[i-1][j].empty() || !LU[i-1][j-1].empty())){
PII u=L[i][j-1].front(),v=U[i-1][j].front(),w=LU[i-1][j-1].front();
int d1=calc(u,{i,j}),d2=calc(v,{i,j}),d3=calc(w,{i,j}),mind=min({d1,d2,d3}); //取最小的那一个
if(mind==d1 && !L[i][j-1].empty()){
L[i][j-1].pop();
if(flag[ a[u.fi][u.se] ]) continue; //出现过就忽略了
LU[i][j].push(u);
flag[ a[u.fi][u.se] ]=true;
}
else if(mind==d2 && !U[i-1][j].empty()){
U[i-1][j].pop();
if(flag[ a[v.fi][v.se] ]) continue;
LU[i][j].push(v);
flag[ a[v.fi][v.se] ]=true;
}
else{
LU[i-1][j-1].pop();
if(flag[ a[w.fi][w.se] ])continue;
LU[i][j].push(w);
flag[ a[w.fi][w.se] ]=true;
}
}
L[i][j-1].head=t1,U[i-1][j].head=t2,LU[i-1][j-1].head=t3;
for(int k=LU[i][j].head;k<=LU[i][j].tail;k++){
PII u=NumToPair( LU[i][j].q[k] );
flag[a[u.fi][u.se]]=false;
}
int tmp=min(i,j);
if(LU[i][j].size()==q+1) tmp=min(tmp,calc( NumToPair(LU[i][j].q[LU[i][j].tail]) , {i,j} )-1);
ans[tmp]++;
}
}
for(int i=n;i>=1;i--) ans[i]+=ans[i+1];
for(int i=1;i<=n;i++) printf("%d\n",ans[i]);
return 0;
}
39.CF1276D Tree Elimination
神仙分类讨论树形DP题,按照连向父亲的边什么时候被删的分类讨论一下,因为 LaTex 打起来太烦了,所以具体看题解区的吧。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5,mod=998244353;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n;
vector<int> G[N]; //vector存边天然优势:编号大的在后面
int f[N][4],pre[N],suf[N];
void dfs(int u,int fa){
bool flag=false; //编号是否比 (u,fa) 大
f[u][1]=f[u][3]=1;
for(int v:G[u]){
if(v==fa){
flag=true;
continue;
}
dfs(v,u);
(f[u][3]*=(f[v][0]+f[v][1])%mod)%=mod;
if(!flag){
(f[u][1]*=(f[v][0]+f[v][1])%mod)%=mod; //此时 u 还在
}
else{
(f[u][1]*=(f[v][0]+f[v][2]+f[v][3])%mod)%=mod; //此时 u 已经没了
}
}
pre[0]=1;
for(int i=1;i<=G[u].size();i++){
int v=G[u][i-1];
if(v==fa){
pre[i]=pre[i-1];
continue;
}
(pre[i]=pre[i-1]*(f[v][0]+f[v][1])%mod)%=mod;
}
suf[G[u].size()+1]=1;
for(int i=G[u].size();i>=1;i--){
int v=G[u][i-1];
if(v==fa){
suf[i]=suf[i+1];
continue;
}
(suf[i]=suf[i+1]*(f[v][0]+f[v][2]+f[v][3])%mod)%=mod;
}
f[u][0]=f[u][2]=0;
flag=false;
for(int i=1;i<=G[u].size();i++){
int v=G[u][i-1];
if(v==fa){
flag=true;
continue;
}
if(!flag){
(f[u][0] += (f[v][2]+f[v][3])%mod * pre[i-1]%mod * suf[i+1]%mod)%=mod;
}
else{
(f[u][2] += (f[v][2]+f[v][3])%mod * pre[i-1]%mod * suf[i+1]%mod)%=mod;
}
}
}
signed main(){
n=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
G[u].push_back(v),G[v].push_back(u);
}
dfs(1,0);
printf("%lld\n",(f[1][0]+f[1][2]+f[1][3])%mod);
return 0;
}
40.P1081 [NOIP2012 提高组] 开车旅行
经典倍增优化DP题。
-
预处理:
\(a[i],b[i]\) 分别表示 \(A/B\) 开车从 \(i\) 开始,下一个到达的城市。
用 multiset 维护即可,不赘述 -
DP:
- \(f[i][j][k]\) 表示行驶 \(2^i\) 天,从城市 \(j\) 开始,\(k\) 先开车会到的城市。
- \(sa[i][j][k]\) 表示行驶 \(2^i\) 天,从城市 \(j\) 开始,\(k\) 先开车,小A开的距离。
- \(sb[i][j][k]\) 表示行驶 \(2^i\) 天,从城市 \(j\) 开始,\(k\) 先开车,小B开的距离。
注意当 \(i=0\) 时,\(2^0=1\)为奇数,转移时要注意开车的人会变。其余就正常的转移
-
calc函数:
\(calc(s,x)\) 表示从 \(s\) 开始,最多行驶 \(x\),小A和小B分别会行驶的距离,倍增即可 -
回答询问:
询问一:只会问一次,暴力枚举起点。
询问二:直接输出 \(calc(si,xi)\)。
code
#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
#define int long long
using namespace std;
const int N=1e5+5,M=(1<<17)+5,inf=2e14;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,h[N];
int a[N],b[N];
multiset<PII> s;
multiset<PII>::iterator it1,it2;
int dist(int x,int y){
if(x==0||y==0) return inf;
return abs(h[x]-h[y]);
}
int u;
bool cmp1(PII x,PII y){
if(dist(x.se,u)==dist(y.se,u)) return x.fi<y.fi;
return dist(x.se,u)<dist(y.se,u);
}
void Init(){
// return;
s.insert({inf,0}),s.insert({inf,0}),s.insert({-inf,0}),s.insert({-inf,0});
//防止越界
for(int i=n;i>=1;i--){
PII tmp[6];
s.insert({h[i],i});
it1=it2=s.find({h[i],i});
--it1; tmp[1]=*it1;
--it1; tmp[2]=*it1;
++it2; tmp[3]=*it2;
++it2; tmp[4]=*it2;
u=i;
sort(tmp+1,tmp+4+1,cmp1);
a[i]=tmp[2].se,b[i]=tmp[1].se;
}
}
int f[20][N][2],sa[20][N][2],sb[20][N][2];
void DP(){
for(int i=1;i<=n;i++){
f[0][i][0]=a[i],f[0][i][1]=b[i];
sa[0][i][0]=dist(i,a[i]),sa[0][i][1]=0;
sb[0][i][1]=dist(i,b[i]),sb[0][i][0]=0;
}
for(int i=1;i<=17;i++){
for(int j=1;j<=n;j++){
for(int k=0;k<=1;k++){
if(i==1){
f[i][j][k]=f[i-1][ f[i-1][j][k] ][1-k];
sa[i][j][k]=sa[i-1][j][k] + sa[i-1][ f[i-1][j][k] ][1-k];
sb[i][j][k]=sb[i-1][j][k] + sb[i-1][ f[i-1][j][k] ][1-k];
}
else{
f[i][j][k]=f[i-1][ f[i-1][j][k] ][k];
sa[i][j][k]=sa[i-1][j][k] + sa[i-1][ f[i-1][j][k] ][k];
sb[i][j][k]=sb[i-1][j][k] + sb[i-1][ f[i-1][j][k] ][k];
}
}
}
}
}
PII calc(int s,int x){
int suma=0,sumb=0,sum=0;
for(int i=17;i>=0;i--){
if(f[i][s][0]&&(sum+sa[i][s][0]+sb[i][s][0])<=x){
suma+=sa[i][s][0],sumb+=sb[i][s][0],sum=suma+sumb;
s=f[i][s][0];
}
}
return {suma,sumb};
}
struct frac{
int a,b,id;
};
bool cmp(frac x,frac y){
if(x.b==y.b&&x.b==0) return h[x.id]>h[y.id];
if(y.b==0) return true;
if(x.b==0) return false;
if(x.a*y.b==y.a*x.b) return h[x.id]>h[y.id];
return x.a*y.b<y.a*x.b;
}
void solve1(){
int x0=read();
frac ming={1,0,0};
for(int i=1;i<=n;i++){
int s1=calc(i,x0).fi,s2=calc(i,x0).se;
if(cmp({s1,s2,i},ming)) ming={s1,s2,i};
}
printf("%lld\n",ming.id);
}
void solve2(){
int T=read();
while(T--){
int s=read(),x=read();
printf("%lld %lld\n",calc(s,x).fi,calc(s,x).se);
}
}
signed main(){
n=read();
h[0]=-inf;
for(int i=1;i<=n;i++) h[i]=read();
Init();
DP();
solve1();
solve2();
return 0;
}
41.P9197 [JOI Open 2016] 摩天大楼
其实这个在动态规划题单一应该就要写了,但是太懒了,所以拖到现在。
套路和 [CEOI2016] kangaroo 有点类似(在第一个题单里),所以建议先看那题。
那我们先列出状态: \(f[i][j][k][0/1][0/1]\) 表示从大到小放到第 \(i\) 个数,一共有 \(j\) 个连续段,题目里的式子计算结果为 \(k\),放/没放第一个,放/没放最后一个的方案数。
但这样如果我们每一次新放进来一个数,只是计算他和他两边的数新增的贡献,我们还需要记录整个序列的哪些位置填了哪些数,才能转移动 \(k\),但这样状态就炸了。所以我们考虑转换一下计算 \(|f_1-f_2| + |f_2-f_3| +...+ |f_{N-1}-f_N|\) 的计算方法。
假如最后是这么个填数方案,横坐标是下标,纵坐标是数值。
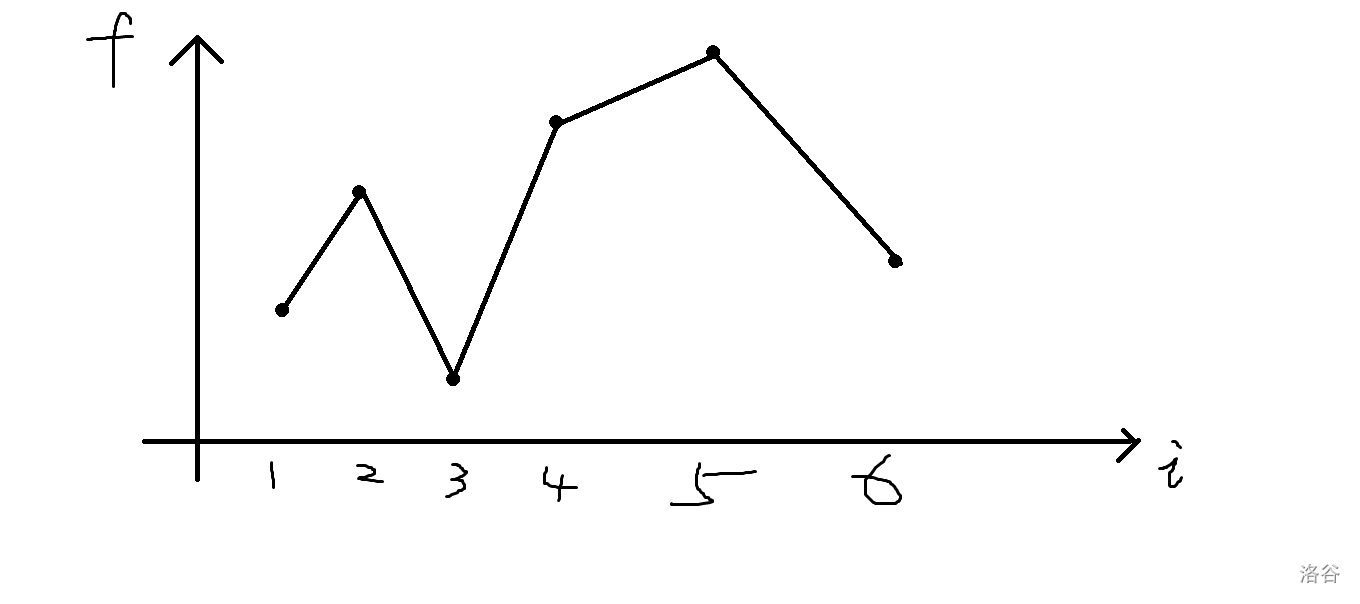
所以当我们从大到小填到第四个数的时候(即图中的\(f_6\)),我们按照原始的方法其实只计算了图中绿色的线段的值。
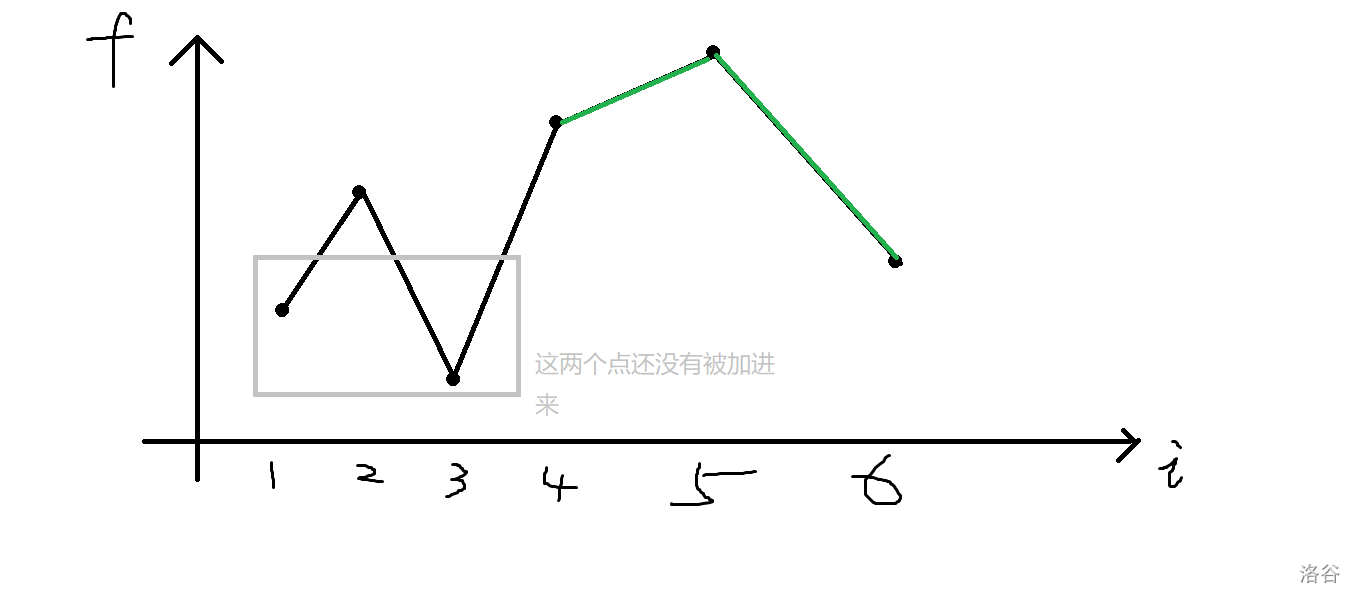
这就使得我们再加进第五个点的时候很不好计算多出来的答案,所以我们计算答案的方式变为:
当新放进来一个数 \(a_i\) 时,假设现在的段数是 \(j\),那么把答案累加上 \((a_{i-1}-a_i) \times (2j)\),意思是每一段自动在两侧延申 \((a_{i-1}-a_i)\),也可以看作是提前计算贡献。
这样当我们从大到小填到第四个数的时候,我们其实就计算了图中蓝色部分的线段了。
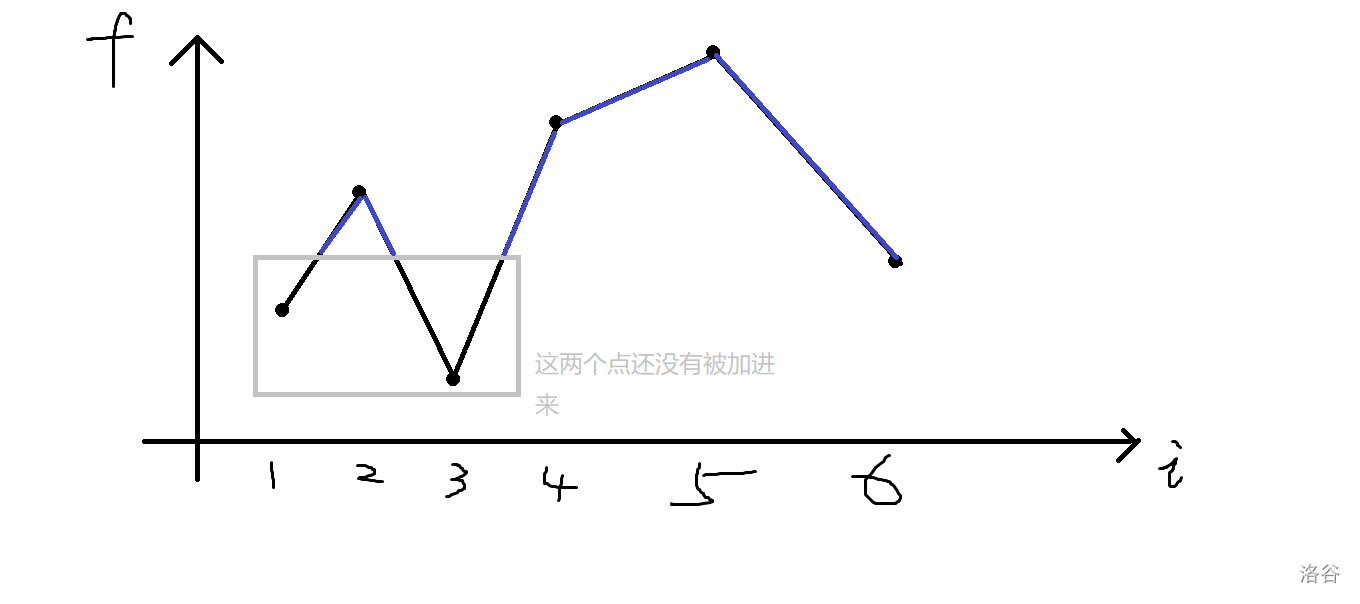
但这样还是会有个小问题,就是在加第\(5\)个点时,按照上述算法,多出来的答案是图中红色加上黄色线段。
但其实黄色线段是没有的。
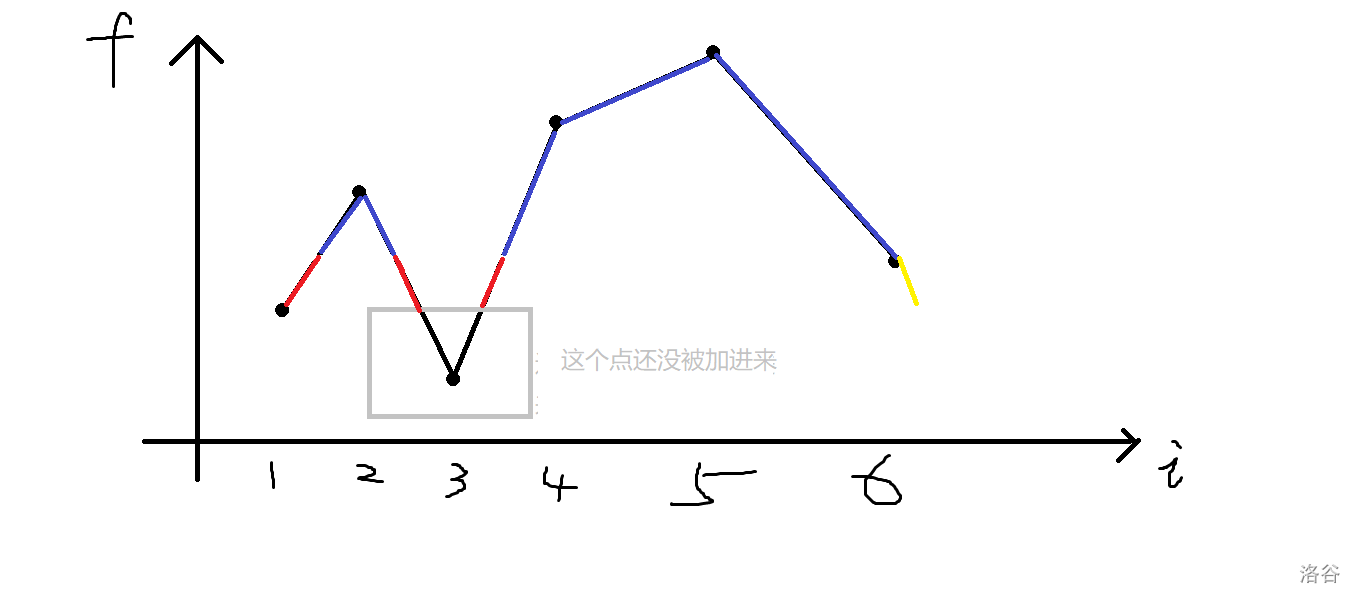
解决办法也比较简单,在开头和结尾已经放了的情况下转移特判一下即可。
具体细节见代码。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5,mod=1e9+7;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,L,a[105];
int f[105][105][1005][2][2];
/*
f[i][j][k][0/1][0/1]表示从大到小放到第 i 个数,一共有j个连续段,题目里的式子计算结果为 k,放/没放第一个,放/没放最后一个
*/
signed main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n=read(),L=read();
for(int i=1;i<=n;i++) a[i]=read();
if(n==1){
cout<<1<<'\n';
return 0; // 此时它又是开头,又是结尾
}
sort(a+1,a+n+1,greater<int>());
f[0][0][0][0][0]=1;
for(int i=0;i<=n;i++){
for(int j=0;j<=i;j++){
for(int k=0;k<=L;k++){
int sum; //新增贡献
//从f[i][j][k][0][0]转移
sum=k + 2 * j * (a[i] - a[i+1]);
if(sum<=L&&sum>=0){
//1.i+1放开头
( f[i + 1][j + 1][sum][1][0] += f[i][j][k][0][0] ) %= mod; //自成一段
( f[i + 1][j][sum][1][0] += f[i][j][k][0][0] ) %= mod; //粘在一段前面
//2.i+1放结尾
( f[i + 1][j + 1][sum][0][1] += f[i][j][k][0][0] ) %= mod; //自成一段
( f[i + 1][j][sum][0][1] += f[i][j][k][0][0] ) %= mod; //粘在一段后面
//3.i+1放中间
( f[i + 1][j + 1][sum][0][0] += (j + 1) * f[i][j][k][0][0] % mod ) %= mod; //自成一段
( f[i + 1][j][sum][0][0] += 2 * j * f[i][j][k][0][0] % mod ) %= mod; //粘在一段前面/后面
( f[i + 1][j - 1][sum][0][0] += (j - 1) * f[i][j][k][0][0] % mod) %= mod; //把两段粘在一起
}
//从f[i][j][k][1][0]转移
sum=k + (2 * j - 1) * (a[i] - a[i+1]);
if(sum<=L&&sum>=0){
//1.i+1放结尾
( f[i + 1][j + 1][sum][1][1] += f[i][j][k][1][0] ) %= mod; //自成一段
( f[i + 1][j][sum][1][1] += f[i][j][k][1][0] ) %= mod; //粘在一段后面
//2.i+1放中间,不能放开头了
( f[i + 1][j + 1][sum][1][0] += j * f[i][j][k][1][0] % mod ) %= mod; //自成一段
( f[i + 1][j][sum][1][0] += (2 * j - 1) * f[i][j][k][1][0] % mod ) %= mod; //粘在一段前面/后面
( f[i + 1][j - 1][sum][1][0] += (j - 1) * f[i][j][k][1][0] % mod) %= mod; //把两段粘在一起
}
//从f[i][j][k][0][1]转移
sum=k + (2 * j - 1) * (a[i] - a[i+1]);
if(sum<=L&&sum>=0){
//1.i+1放开头
( f[i + 1][j + 1][sum][1][1] += f[i][j][k][0][1] ) %= mod; //自成一段
( f[i + 1][j][sum][1][1] += f[i][j][k][0][1] ) %= mod; //粘在一段前面
//2.i+1放中间,不能放结尾了
( f[i + 1][j + 1][sum][0][1] += j * f[i][j][k][0][1] % mod ) %= mod; //自成一段
( f[i + 1][j][sum][0][1] += (2 * j - 1) * f[i][j][k][0][1] % mod ) %= mod; //粘在一段前面/后面
( f[i + 1][j - 1][sum][0][1] += (j - 1) * f[i][j][k][0][1] % mod) %= mod; //把两段粘在一起
}
//从f[i][j][1][1]转移
sum=k + (2 * j - 2) * (a[i] - a[i+1]);
if(sum<=L&&sum>=0){
//1.i+1放中间,不能放开头和结尾了
( f[i + 1][j + 1][sum][1][1] += (j - 1) * f[i][j][k][1][1] % mod ) %= mod; //自成一段
( f[i + 1][j][sum][1][1] += (2 * j - 2) * f[i][j][k][1][1] % mod ) %= mod; //粘在一段前面/后面
( f[i + 1][j - 1][sum][1][1] += (j - 1) * f[i][j][k][1][1] % mod) %= mod; //把两段粘在一起
}
}
}
}
int ans=0;
for(int i=0;i<=L;i++){
(ans += f[n][1][i][1][1]) %= mod;
}
printf("%lld\n",ans);
return 0;
}
42.Count The Repetitions*
\([S2,M]=[s2,n2*M]\)。
找到最大的 \(M\) 也就是找到最大的 \(M'\) 使得 \([S2,M']\) 是 \([s1,n1]\) 的子序列。答案那就是 \(\lfloor \frac {M'} {n2} \rfloor\) 。
无解的判定:如果 \(s2\) 中的字符没有全部在 \(s1\) 中出现就无解。否则至多重复 \(s1\) \(len2\) 次就可以得到一个 \(s2\) (\(len2\) 是 \(s2\) 的长度)。
预处理:\(g[i]\) 表示从 \(s1\) 的第 \(i\) 位开始,至少接需要多少个字符才能凑出一个 \(s2\),注意不是接多少个 \(s1\),而是字符,\(O(len^3)\) 暴力即可
设 \(f[i][s]\) 表示从 \(s1\) 的第 \(s\) 个开始,凑出 \(2^i\) 个 \(s2\) 需要多少个字符,转移显然。
倍增优化求答案的过程即可。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
char s1[105],s2[105];
int n1,n2,len1,len2;
int g[105],f[40][105];
bool stater;
void Init(){
memset(g,0x3f,sizeof g);
memset(f,0x3f,sizeof f);
len1=strlen(s1),len2=strlen(s2);
stater=true;
string s;
for(int i=1;i<=len2;i++) s=s+s1;
for(int i=0;i<len1;i++){
int k=0;
for(int j=i,cnt=1;j<s.size();j++,cnt++){
if(s[j]==s2[k]){
k++;
if(k==len2){
g[i]=cnt;
break;
}
}
}
if(g[i]>s.size()){
stater=false;
return;
}
else f[0][i]=g[i];
}
for(int t=1;t<=30;t++){
for(int i=0;i<len1;i++){
f[t][i]=f[t-1][i]+f[t-1][(i+f[t-1][i])%len1];
}
}
}
void work(){
if(!stater){
puts("0");
return;
}
int maxn=len1*n1,sum=0,res=0,pos=0;
for(int i=30;i>=0;i--){
if(f[i][pos]+sum<=maxn){
sum+=f[i][pos];
pos=(pos+f[i][pos])%len1;
res+=pow(2,i);
}
}
printf("%lld\n",res/n2);
}
signed main(){
while(scanf("%s %lld\n%s %lld",s2,&n2,s1,&n1)==4){
Init();
work();
}
return 0;
}
43.CF1788E Sum Over Zero
\(f[i]\):表示区间 \([1,i]\) 上的最大值 (一定要选 \(i\))。
\(pre[i]\):表示 \(max{f[0],f[2],...,f[i]}\)。
\(s[i]=a1+a2+...+ai\)。
转移:\(f[i]=max_{0 \le j \le i-1,si-sj \ge 0}({i-j+pre[j]})\)
\(f[i]\) 转移的优化:在每个 \(s[j]\) 上记录最大的 \(pre[j]-j\) , 转移时在线段树上查询 \((-inf,si]\) 的最大值。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5,MAXN=2e14;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,a[N];
int s[N],pre[N],f[N];
int dis[N],m;
int Dis(int x){
return lower_bound(dis+1,dis+m+1,x)-dis;
}
struct node{
int l,r,maxn;
};
struct SegmentTree{
node t[10000005];
void pushup(int p){
t[p].maxn=max(t[p<<1].maxn,t[p<<1|1].maxn);
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r,t[p].maxn=LLONG_MIN;
if(l==r) return;
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
pushup(p);
}
void change(int p,int x,int val){
if(t[p].l==t[p].r){
t[p].maxn=max(t[p].maxn,val);
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(x<=mid){
change(p<<1,x,val);
}
else{
change(p<<1|1,x,val);
}
pushup(p);
}
int ask(int p,int l,int r){
if(l<=t[p].l&&t[p].r<=r){
return t[p].maxn;
}
int mid=(t[p].l+t[p].r)>>1,res=LLONG_MIN;
if(l<=mid) res=max(res,ask(p<<1,l,r));
if(r>mid) res=max(res,ask(p<<1|1,l,r));
return res;
}
}Seg;
signed main(){
int ming=0;
n=read();
dis[n+1]=0;
for(int i=1;i<=n;i++) a[i]=read(),s[i]=s[i-1]+a[i],dis[i]=s[i],ming=min(ming,s[i]);
sort(dis+1,dis+n+1+1);
m=unique(dis+1,dis+n+1+1)-dis-1;
Seg.build(1,1,m);
f[0]=0;
pre[0]=0;
Seg.change(1,Dis(s[0]),pre[0]);
for(int i=1;i<=n;i++){
f[i]=Seg.ask(1,Dis(ming),Dis(s[i]))+i;
pre[i]=max(pre[i-1],f[i]);
Seg.change(1,Dis(s[i]),pre[i]-i);
}
printf("%lld\n",pre[n]);
return 0;
}
44.CF1799D2 Hot Start Up (hard version)
CF1799D2 Hot Start Up (hard version)
压缩状态优化DP 。
\(f[i][x][y]\) 表示处理完第 \(i\) 个程序,目前第一个 CPU 里运行的程序种类是 \(x\),第二个里运行的程序种类是 \(y\)。
因为 \(x,y\) 中一定有一个是 \(ai\),考虑把第一维去掉,那么有转移(很明显能用 \(hot\) 就不用 \(cold\)):
- \(f[x][y]+cold[ai] \to f[ai][y]\)
- \(f[x][y]+cold[ai] \to f[x][ai]\)
- \(f[x][ai]+hot[ai] \to f[x][ai]\)
- \(f[ai][x]+hot[ai] \to f[ai][x]\)
直接跑是 \(O(n\times k^2)\) 的
我们会发现每次转移时,都只会转移到 \(f[ai][x]\) 或 \(f[x][ai]\)。同理在进行转移的时候也只有 \(f[a[i-1]][x]\) 和 \(f[x][a[i-1]]\) 中会有值。只需要枚举 \(x\) ,进行转移即可。
因为两个 CPU 本质相同,所以 \(f[x][y]\) 显然等于\(f[y][x]\),即转移优化成: (默认 \(a[i-1] \ne a[i]\),如果相等直接全部加 \(hot[ai]\) 即可)
- \(f[a[i-1]][x]+cold[ai] \to f[a[i-1]][ai]\) (此时如果 \(x=ai\) 的话,肯定不如第3条优)
- \(f[a[i-1]][x]+cold[ai] \to f[ai][x]\)
- \(f[a[i-1]][ai]+hot[ai] \to f[a[i-1]][ai]\)
可以通过简单版。
还是因为 \(f[x][y]=f[y][x]\),所以转移到 \(f[ai][x]\) 和 转移到 \(f[x][ai]\) 是一样的,所以我们考虑进一步压缩状态用 \(f[x]\) 代替 \(f[ai][x]\),那么上面那三个转移式子就优化成:
- 如果 \(a[i-1] \ne ai\)
- \(f[x]+cold[ai] \to f[a[i-1]]\)
- \(f[x]+cold[ai] \to f[x]\)
- \(f[ai]+hot[ai] \to f[a[i-1]]\)
分别进行优化:
- 转移到的目标是定的,直接维护全局最小值进行转移即可。
- 相当于每个点都加一个 \(cold[ai]\),我们用 \(add\) 记录一下全局累加标记即可。
- 下标都给定了,直接转移。
- 如果 \(a[i-1]=ai\),直接 \(add+=hot[ai]\)。
几个注意:
- 如果进行了转移1或3,那此时是不用加上转移2的 \(cold[ai]\) 的,要先减掉 \(cold[ai]\)。
- 维护新的全局最小值时全部重新跑一遍肯定不太对,我们会发现这三个转移中只有转移二会转移到 \(f[x]\),但是 \(f[x]+cold[ai]\) 不仅会转移给 \(f[x]\),也会转移给 \(f[a[i-1]]\),而 \(f[a[i-1]]\) 还可以通过 \(f[ai]+hot[ai]\) 转移,所以 \(f[a[i-1]]\) 一定是全局最小值,只要用它更新即可。
3.一开始 \(f[0]=0\), 其余全是 \(inf\)。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+5,inf=3e14+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int T;
int n,k,a[N],cold[N],hot[N],f[N];
void work(){
n=read(),k=read();
for(int i=1;i<=n;i++) a[i]=read();
for(int i=1;i<=k;i++) cold[i]=read(),f[i]=inf;
for(int i=1;i<=k;i++) hot[i]=read();
f[0]=0;
int add=0,ming=0;
for(int i=1;i<=n;i++){
if(a[i]!=a[i-1]){
add+=cold[a[i]];
f[a[i-1]]=min({f[a[i-1]] , ming+cold[a[i]]-cold[a[i]] , f[a[i]]+hot[a[i]]-cold[a[i]]});
ming=f[a[i-1]];
}
else add+=hot[a[i]];
}
printf("%lld\n",ming+add);
}
signed main(){
T=read();
while(T--) work();
return 0;
}
45.CF1304F2 Animal Observation (hard version)
CF1304F2 Animal Observation (hard version)
题意简化:给定一个 \(n\times m\) 的矩形,每一行选择一个点,并以这个点为左上角框出一个 \(2\times k\) 的小矩形,求所有小矩形的并所覆盖的数字之和的最大值。
设 \(m'=m-k+1\),显然每个点的纵坐标不会超过 \(m'\)。
设 \(f[i][j]\) 表示第 \(i\) 行选第 \(j\) 个点,前 \(i\) 行的最大值。
如果可以重复,那 DP 方程容易得出:
\(f[i][j]=max_{1\le x\le m'}(f[i-1][x]+pre[i][x+k-1]-pre[i][x-1]) + pre[i][j+k-1] - pre[i][j-1]\), \(pre[i]\) 是第 \(i\) 行的前缀和。
前面一项容易维护,从而 \(O(1)\) 转移,总时间复杂度 \(O(n^2)\)。
考虑去掉重复贡献。
设 \(f[i][j]\) 表示第 \(i\) 行选第 \(j\) 个点,前 \(i\) 行的最大值(不能重复贡献)。
又设 \(g[i][j]=f[i][j]+pre[i+1][j+k-1]-pre[i+1][j-1]\)。
则转移方程可以写成:
\(f[i][j]=max_{1\le x \le m'}{g[i-1][x]} + pre[i][j+k-1] - pre[i][j-1] - 重复贡献的部分\)。
考虑把重复贡献的部分在 max 里就去掉,一个点 \(a[i][y] (j\le y\le j+k-1)\) 重复贡献在:
\(g[i-1][y-k+1],...,g[i-1][y-1],g[i-1][y]\)。
只需要把他们全部减去 \(a[i][y]\) 即可,支持区间减,区间查最大值的是什么? 线段树。转移完之后再加回去。
但这样是 \(O(n \times m \times k \times \log m)\),因为要对每个 \(j<=y<=j+k-1\) 都做一遍区间减。但是当 \(j\) 从 \(j\) 变到 \(j+1\),其实只有 \(j\) 这个位置不再被重复贡献,\(j+1+k-1\) 这个位置新加进来,所以就好了。
所以 \(O(n\times m\times \log m)\)。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e4+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,m,k,a[55][N],pre[55][N];
int f[55][N],g[N];
struct node{
int l,r,maxn,add;
void tag(int d){
maxn+=d;
add+=d;
}
};
struct SegmentTree{
node t[N<<2];
void pushup(int p){
t[p].maxn=max(t[p<<1].maxn,t[p<<1|1].maxn);
}
void spread(int p){
if(t[p].add){
t[p<<1].tag(t[p].add);
t[p<<1|1].tag(t[p].add);
t[p].add=0;
}
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r,t[p].add=0; //add也要清空
if(l==r){
t[p].maxn=g[l];
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
pushup(p);
}
void change(int p,int l,int r,int d){
if(l<=t[p].l&&t[p].r<=r){
t[p].tag(d);
return;
}
spread(p);
int mid=(t[p].l+t[p].r)>>1;
if(l<=mid) change(p<<1,l,r,d);
if(r>mid) change(p<<1|1,l,r,d);
pushup(p);
}
}Seg;
signed main(){
n=read(),m=read(),k=read();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
a[i][j]=read();
pre[i][j]=pre[i][j-1]+a[i][j];
}
}
int m1=m-k+1;
for(int i=1;i<=n;i++){
for(int j=1;j<=m1;j++){
if(i!=1){
if(j==1){
for(int y=j;y<=j+k-1;y++) Seg.change(1,1,y,-a[i][y]);
}
else{
Seg.change(1,max(1ll,j-1-k+1),j-1,a[i][j-1]);
Seg.change(1,j,j+k-1,-a[i][j+k-1]);
}
}
f[i][j]=Seg.t[1].maxn+pre[i][j+k-1]-pre[i][j-1];
g[j]=f[i][j]+pre[i+1][j+k-1]-pre[i+1][j-1];
}
Seg.build(1,1,m1);
}
int ans=0;
for(int i=1;i<=m1;i++) ans=max(ans,f[n][i]);
printf("%lld\n",ans);
return 0;
}
46.夏虫(summer)
题意简述:
用 \(n\) 个虫子,每个虫子有一个狡猾值 \(a_i\),一开始你会站在一个虫子 \(x\) 前,将初始能力值设为 \(a_x\),并捕捉它,接下来你可以重复执行三种操作,直到捕捉完所有昆虫:
设当前捕捉到了区间 \([l,r]\) 的昆虫,能力值为 \(v\)
- 若 \(l \ne 1\) 并且 \(a_{l−1} \le v\) ,那么可以花费 \(1\) 单位精力捕捉 \(l−1\) 号夏虫;
- 若 \(r \ne n\) 并且 \(a_{r+1} \le v\) ,那么她们可以花费 \(1\) 单位精力捕捉 \(r + 1\) 号夏虫;
- 花费 \(k\) (\(k\) 是定值)单位精力使得捕虫网的能力值为 \(min(a_{l−1}, a_{r+1})\)。在这里定义 \(a_0 = a_{n+1} = inf\)。
有 \(Q\) 次询问,每次给定 \(x,l,r\) 表示交换 \(x,x+1\) 两只昆虫的位置后,询问你初始站在 \([l,r]\) 内的每只昆虫前的最小花费精力的和。注意交换操作是永久的,即会对后面的询问产生影响。
题解:
首先操作 \(1\) 和操作 \(2\) 肯定加起来要做 \(n-1\) 次,所以只需要看操作 \(3\) 要几次。
容易用单调栈维护处 \(L[i]/R[i]\) 表示 \(a[i]\) 作为最大值的区间。
那么设 \(f[i]\) 表示以 \(i\) 为开始需要多少次操作 \(3\),不妨设 \(a[L[i]-1] < a[R[i]+1]\),则 \(f[i]=f[L[i]-1] + 1\)。
所以按照值域从大到小 \(dp\) 即可做到 \(O(n)\) 求解单次询问,那么时间复杂度 \(O(nQ)\),有 40 分。
但是如果按照这种转移的求法,不是很好在每次修改后维护 \(f\),考虑换一个求法:
设 \(A_x\) 表示 \(a[1],a[2],...,a[x]\) 的后缀最大值的集合。\(B_x\) 表示 \(a[x],a[x+1],...,a[n]\) 的前缀最大值的集合。
那么答案就是 \(|A_x \cup B_x| - 1\),-1 是因为 \(a[x]\) 自己是不用算的,这个式子应该还好理解,就不证了。
我们维护两棵线段树 \(Seg1,Seg2\)。\(Seg1\) 维护 \(a\) 序列,\(Seg2\) 维护 \(f\) 。
注意:我们是无法去维护 \(A,B\) 集合的,即不能对每个数开两个 \(multiset\),当然因为无法维护,我们也不需要真的在集合里删掉某些数(这是好的)
假设现在交换了 \(a[x],a[x+1]\),去考虑会影响哪些数的 \(A,B\) 集合。
- \(a[x]<a[x+1]\)
- 对于 \(1 \le i \le x-1\) 的 \(i\),它们的 \(A\) 集合显然是不变的,但是 \(B\) 集合里有可能原来有 \(a[x]\),现在就没了(因为 \(a[x+1]\) 跑到 \(a[x]\) 前面了)。
首先我们需要知道哪些数的 \(B\) 集合原来有 \(a[x]\),容易知道一定是 \([l,x-1]\) 这一段区间的数,其中每个数都 \(<a[x]\),注意如果 \(=a[x]\) 是不算的,因为 \(=a[x]\) 的话他的 \(B\) 集合里仍然有 \(a[x]\)。
求这个 \(l\) 在 \(Seg1\) 上线段树二分即可,但是要知道 \(i \in [l,x-1]\) 的 \(f[i]\) 是否改变还要看 \(A[i]\) 里是否有 \(a[x]\),这里不用也不能去每个数判断一遍,注意到对于 \(A[i]\),他在 \(a[l],a[l+1],..,a[i]\) 的后缀\(max\)里肯定是没有 \(a[x]\) 的,所以只需要去看 \(a[l-1]\) 是否 \(=a[x]\) 即可。
如果 \(a[l-1] \ne a[x]\)的话他们的 \(f[i]-1\),即在 \(Seg2\) 上区间 \(-1\)。 - 对于 \(i\ge x+2\),他们的 \(B\) 集合不变,\(A\) 集合要改变的是一段区间 \([x+2,r]\),他们都 \(<a[x]\),它们的 \(A\) 集合里会多出 \(a[x]\)。
同理求 \(r\) 只需要线段树二分。判断 \(f\) 是否要 \(+1\) 只需要看 \(a[r+1]\) 是否 \(=a[x]\)。 - 对于 \(i=x,i=x+1\),注意到这个时候我已经求出了其他 \(i\) 的 \(f\) 值,所以直接按照最初的 \(f[i]=f[(L[i]-1) / (R[i]+1)] + 1\) 转移即可,\(L[i],R[i]\) 也可线段树二分求。注意要按照从大到小的顺序 DP
- \(a[x]>a[x+1]\) ,类似分类讨论,不想写了。
用上面的写法是 \(O(n + Qlogn)\) 但是因为不知道怎么写这个线段树二分,所以这边想到了有两种做法:
- 来自大佬 @RiceFruit 的: 在 \([l,r]\) 中查询第一个满足 \(max(a[i],a[i+1],..,a[r]) \le val\) 的位置 \(i\),就先把 \([l,r]\) 拆成 \(log\) 个区间,然后先从后往前扫一遍判断在哪一个子树内,这样对于一整个子树的求解是好做的。
- 暴力二分用线段树查询的做法,所以是双 \(log\) 的。
一看就方法\(2\)好写,所以一开始写 \(O(Q \times log^2n)\),但是这样要跑 \(1.6\)s,当时看着自己TLE的 \(8k\) 代码人都炸了。
所以还是写第一种吧。
代码有亿点点长,个人码风问题,但真的感觉写出来也是挺不容易的。
Swap函数那里码风突变是因为不加空格看着太恶心了。
code
#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
#define int long long
using namespace std;
const int N=1e5+5,inf=1e18;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,k,T,a[N];
PII t[N];
int L[N],R[N],f[N];
stack<int> st;
struct node1{
int l,r,maxn;
};
struct SegmentTree1{
node1 t[N<<2];
vector<int> v; //存区间用
void pushup(int p){
if(t[p<<1].maxn>t[p<<1|1].maxn) t[p].maxn=t[p<<1].maxn;
else t[p].maxn=t[p<<1|1].maxn;
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r;
if(l==r){
t[p].maxn=a[l];
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
pushup(p);
}
int ask(int p,int l,int r){
if(l<=t[p].l&&t[p].r<=r){
return t[p].maxn;
}
int mid=(t[p].l+t[p].r)>>1,maxn=0;
if(l<=mid) maxn=max(maxn,ask(p<<1,l,r));
if(r>mid) maxn=max(maxn,ask(p<<1|1,l,r));
return maxn;
}
void Get_range(int p,int l,int r){
if(l<=t[p].l&&t[p].r<=r){
v.push_back(p);
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(l<=mid) Get_range(p<<1,l,r);
if(r>mid) Get_range(p<<1|1,l,r);
}
int lower1(int p,int val,int op){
if(t[p].l==t[p].r){
if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) return t[p].l;
else return n+1;
}
if( (op==0&&t[p<<1|1].maxn<val) || (op==1&&t[p<<1|1].maxn<=val) ) return min(lower1(p<<1,val,op) , t[p<<1|1].l);
else return lower1(p<<1|1,val,op);
}
int lower2(int p,int val,int op){
if(t[p].l==t[p].r){
if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) return t[p].l;
else return 0;
}
if( (op==0&&t[p<<1].maxn<val) || (op==1&&t[p<<1].maxn<=val) ) return max(t[p<<1].r , lower2(p<<1|1,val,op));
else return lower2(p<<1,val,op);
}
int ask1(int l,int r,int val,int op){ //在 l~r 中查询第一个满足 max(a[i],a[i+1],..,a[r]) </<= val 的位置
if(l>r) return n+1;
if( (op==0&&a[r]>=val) || (op==1&&a[r]>val) ) return n+1; //先保证有解
v.clear(); //子树下标放这个里面,从左往右放
Get_range(1,l,r);
int ans=r;
for(int i=v.size()-1;i>=0;i--){
int p=v[i];
if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) ans=min(ans,t[p].l); //这里只需要比当前子树的最大值就好了,扫过的那些已经满足了
else{
ans=min(ans,lower1(p,val,op));
break;
}
}
return ans;
}
int ask2(int l,int r,int val,bool op){ //在 l~r 中查询最后一个满足 max(a[l],a[l+1],..,a[i]) </<= val 的位置
if(l>r) return 0;
if( (op==0&&a[l]>=val) || (op==1&&a[l]>val) ) return 0;
v.clear();
Get_range(1,l,r);
int ans=l;
for(int i=0;i<v.size();i++){
int p=v[i];
if( (op==0&&t[p].maxn<val) || (op==1&&t[p].maxn<=val) ) ans=max(ans,t[p].r);
else{
ans=max(ans,lower2(p,val,op));
break;
}
}
return ans;
}
void change(int p,int x,int val){
if(t[p].l==t[p].r){
t[p].maxn=val;
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(x<=mid) change(p<<1,x,val);
else change(p<<1|1,x,val);
pushup(p);
}
}Seg1;
struct node2{
int l,r,sum,add;
void tag(int d){
sum+=(r-l+1ll)*d,add+=d;
}
};
struct SegmentTree2{
node2 t[N<<2];
void pushup(int p){
t[p].sum=t[p<<1].sum+t[p<<1|1].sum;
}
void spread(int p){
if(t[p].add){
t[p<<1].tag(t[p].add);
t[p<<1|1].tag(t[p].add);
t[p].add=0;
}
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r;
if(l==r){
t[p].sum=f[l];
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
pushup(p);
}
void change(int p,int x,int val){
if(t[p].l==t[p].r){
t[p].sum=val;
return;
}
spread(p);
int mid=(t[p].l+t[p].r)>>1;
if(x<=mid) change(p<<1,x,val);
else change(p<<1|1,x,val);
pushup(p);
}
void modify(int p,int l,int r,int d){
if(l<=t[p].l&&t[p].r<=r){
t[p].tag(d);
return;
}
spread(p);
int mid=(t[p].l+t[p].r)>>1;
if(l<=mid) modify(p<<1,l,r,d);
if(r>mid) modify(p<<1|1,l,r,d);
pushup(p);
}
int ask(int p,int l,int r){
if(l<=t[p].l&&t[p].r<=r){
return t[p].sum;
}
spread(p);
int mid=(t[p].l+t[p].r)>>1,res=0;
if(l<=mid) res+=ask(p<<1,l,r);
if(r>mid) res+=ask(p<<1|1,l,r);
return res;
}
int ask2(int p,int x){
if(t[p].l==t[p].r) return t[p].sum;
spread(p);
int mid=(t[p].l+t[p].r)>>1;
if(x<=mid) return ask2(p<<1,x);
else return ask2(p<<1|1,x);
}
}Seg2;
void Init(){
st.push(0);
for(int i=1;i<=n;i++){
while(st.size()&&a[st.top()]<=a[i]) st.pop();
L[i]=st.top()+1ll;
st.push(i);
}
while(st.size()) st.pop();
st.push(n+1);
for(int i=n;i>=1;i--){
while(st.size()&&a[st.top()]<=a[i]) st.pop();
R[i]=st.top()-1ll;
st.push(i);
}
f[0]=f[n+1]=-1ll;
sort(t+1,t+n+1,[](PII x,PII y){return x.fi>y.fi;});
for(int i=1;i<=n;i++){
if(a[L[t[i].se]-1] < a[R[t[i].se]+1]) f[t[i].se]=f[L[t[i].se]-1]+1ll;
else f[t[i].se]=f[R[t[i].se]+1]+1ll;
}
Seg1.build(1,0,n+1);
Seg2.build(1,0,n+1); //虽然查不到 0/n+1 但是可能要用
}
void Swap(int x){
if(a[x]==a[x+1]) return;
if(a[x]<a[x+1]){
int l = Seg1.ask1(1 , x-1 , a[x] , 0);
if(l<=x-1 && a[l-1] != a[x]) Seg2.modify(1 , l , x-1 , -1ll);
int r=Seg1.ask2(x+2 , n , a[x] , 0);
if(r>=x+2 && a[r+1] != a[x]) Seg2.modify(1 , x+2 , r , 1ll);
Seg1.change(1 , x , a[x+1]) , Seg1.change(1 , x+1 , a[x]);
int maxn=a[x+1],ming=a[x];
swap(a[x],a[x+1]);
//先更新大的再更新小的
int L1 = Seg1.ask1(1 , x , maxn , 1) , R1 = Seg1.ask2(x , n , maxn , 1) , F; //注意这个时候 a[x+1] 在 x 的位置
if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
else F = Seg2.ask2(1 , R1+1) + 1ll;
Seg2.change(1 , x , F);
L1 = Seg1.ask1(1 , x+1 , ming , 1) , R1 = Seg1.ask2(x+1 , n , ming , 1) , F; //注意这个时候 a[x] 在 x+1 的位置
if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
else F = Seg2.ask2(1,R1+1) + 1ll;
Seg2.change(1 , x+1 , F);
}
else{ //a[x]>a[x+1]
int l = Seg1.ask1(1 , x-1 , a[x+1] , 0); //此时可能多出来一个 a[x+1]
if(l<=x-1 && a[l-1] != a[x+1]) Seg2.modify(1 , l , x-1 , 1ll);
int r = Seg1.ask2(x+2 , n , a[x+1] , 0);
if(r>=x+2 && a[r+1] != a[x+1]) Seg2.modify(1 , x+2 , r , -1ll);
Seg1.change(1 , x ,a[x+1]) , Seg1.change(1 , x+1 , a[x]);
int maxn=a[x],ming=a[x+1];
swap(a[x],a[x+1]);
int L1 = Seg1.ask1(1 , x+1 , maxn , 1) , R1 = Seg1.ask2(x+1 , n , maxn , 1) , F;
if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
else F = Seg2.ask2(1 , R1+1) + 1ll;
Seg2.change(1 , x+1 , F);
L1 = Seg1.ask1(1 , x , ming , 1) , R1 = Seg1.ask2(x , n , ming , 1) , F;
if( a[L1-1] < a[R1+1] ) F = Seg2.ask2(1 , L1-1) + 1ll;
else F = Seg2.ask2(1 , R1+1) + 1ll;
Seg2.change(1 , x , F);
}
}
signed main(){
freopen("summer.in","r",stdin);
freopen("summer.out","w",stdout);
n=read(),k=read();
for(int i=1;i<=n;i++) a[i]=read(),t[i].fi=a[i],t[i].se=i;
a[0]=a[n+1]=inf;
Init();
T=read();
while(T--){
int x=read(),l=read(),r=read();
Swap(x);
printf("%lld\n",Seg2.ask(1,l,r)*k + (n-1)*(r-l+1));
}
return 0;
}
47.任务安排
弱化版是不用斜率优化的。
设 \(f[i][j]\) 表示前 \(i\) 个任务分成 \(j\) 段的最小花费。
\(f[i][j]=min_{0\le j \le i-1}(f[k][j-1] + s + (S1[i]+s\times j)\times (S2[i]-S2[k]))\)。
\(S1\) 是 \(t\) 的前缀和,\(S2\) 是 \(F\) 的前缀和。
这样是 \(O(n^3)\) 的。
回顾"我的动态规划题单2"中"关路灯"那题,
考虑将 \(s\) 的费用提前计算,只考虑当前这批任务对后面的影响,这样就可以不去记录段数 \(j\) 了。
\(f[i]=min_{0\le j \le i-1}(f[j] + S1[i]\times(S2[i]-S2[j]) + s\times (S2[n]-S2[j]))\)。
时间复杂度\(O(n^2)\)。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,s,t[N],F[N],f[N],S1[N],S2[N];
signed main(){
n=read(),s=read();
for(int i=1;i<=n;i++){
t[i]=read(),F[i]=read();
S1[i]=S1[i-1]+t[i];
S2[i]=S2[i-1]+F[i];
}
memset(f,0x3f,sizeof f);
f[0]=0;
for(int i=1;i<=n;i++){
for(int j=0;j<i;j++){
f[i]=min(f[i],f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]));
}
}
printf("%lld\n",f[n]);
return 0;
}
48.任务安排2
\(f[i]=min_{0\le j \le i-1}(f[j] + S1[i]\times(S2[i]-S2[j]) + s\times (S2[n]-S2[j]))\)。
按照dp的套路,把式子改写一下,只跟 \(j\) 有关和只跟 \(i\) 有关的拎出来:
\(f[i]=min_{0\le j \le i-1}(f[j] - (s+S1[i])\times S2[j]) + s\times S2[n] + S1[i]\times S2[i]\)。
不管后面那一坨,去掉 \(min\) 写成 \(y=kx+b\) 的形式:
\((s+S1[i])\times S2[j] + f[i] = f[j]\)。
所以就用一条斜率为 \((s+S1[i])\) 的直线去切这些形如 \((S2[j] , f[j])\) 的点。
维护出下凸壳之后,注意到因为 \(t_i\) 都是正数,所以斜率 \((s+S1[i])\) 随着 \(i\) 的增大而增大,那根据切点的判定条件,切点也是一定右移的,所以只保留斜率大于 \((s+S1[i])\) 的部分即可。
而且注意到这里的 \(L(i)\) 函数始终是 \(0\),所以就有了一下 O(n) 的做法:
- 用单调队列替换掉单调栈。
- 对于 \(i\),把队头那些斜率 \(\le (s+S1[i])\) 的线段 pop 掉,这样队头的点就是要求的切点。
- 取出队头转移。
- 加入 \(i\),并维护下凸壳。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,s,t[N],c[N],f[N],S1[N],S2[N];
int dq[N],l,r; //单调队列
int x(int j){return S2[j];} //横坐标
int y(int j){return f[j];} //纵坐标
signed main(){
n=read(),s=read();
for(int i=1;i<=n;i++){
t[i]=read(),c[i]=read();
S1[i]=S1[i-1]+t[i];
S2[i]=S2[i-1]+c[i];
}
memset(f,0x3f,sizeof f);
f[0]=0;
l=1,r=0; //初始化空的单调队列
dq[++r]=0;
for(int i=1;i<=n;i++){
while( l<r && ( y(dq[l+1]) - y(dq[l]) ) <= (s + S1[i]) * ( x(dq[l+1]) - x(dq[l]) ) ) l++; //注意是 l<r 而不是 l<=r,因为起码要有两个点才是线段
int j=dq[l];
f[i]=f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]); //这里就用原来的式子就好了,新的那个太大便了
while( l<r && ( y(dq[r]) - y(dq[r-1]) ) * ( x(i) - x(dq[r]) ) >= ( y(i) - y(dq[r]) ) * ( x(dq[r]) - x(dq[r-1]) ) ) r--; //维护凸壳
dq[++r]=i;
}
printf("%lld\n",f[n]);
return 0;
}
49.[SDOI2012] 任务安排
题面都是一样的。
这里 \(t_i\) 可能是负数,所以 \((s+S1[i])\) 不一定单调。
所以求切点要二分,这里还是用的单调队列,其实单调栈也可以。
时间复杂度 O(n log n)。
要注意的是,这里 \(c_i\) 可以等于 \(0\),也就是说也就是会出现横坐标相同的两个点,那么有可能出现原先的斜率是 \(inf\)(即与 \(x\) 轴垂直,但是后面那个在前面那个上面),加进来一个后变成 \(-inf\)(加进来的在原来队尾的下面),但它们的斜率在比较时是一样,如果不把前面那个弹掉,就不满足斜率单调递增了,所以在维护下凸壳时,\(=\) 的情况也要把队尾弹掉(代码中也有注释)。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,s,t[N],c[N],f[N],S1[N],S2[N];
int dq[N],l,r; //单调队列
int x(int j){return S2[j];} //横坐标
int y(int j){return f[j];} //纵坐标
int Binary_search(int K){
int L=l,R=r,mid,res=r; //二分找第一个满足它后面的线段的斜率比 s+S1[i] 大的点y
while(L<=R){
mid=(L+R)>>1;
if(mid<r && y(dq[mid+1]) - y(dq[mid]) > K * ( x(dq[mid+1]) - x(dq[mid]) )) R=mid-1,res=mid;
else L=mid+1;
}
return dq[res];
}
signed main(){
n=read(),s=read();
for(int i=1;i<=n;i++){
t[i]=read(),c[i]=read();
S1[i]=S1[i-1]+t[i];
S2[i]=S2[i-1]+c[i];
}
memset(f,0x3f,sizeof f);
f[0]=0;
l=1,r=0; //初始化空的单调队列
dq[++r]=0;
for(int i=1;i<=n;i++){
int j=Binary_search(s+S1[i]);
f[i]=f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]);
while( l<r && ( y(dq[r]) - y(dq[r-1]) ) * ( x(i) - x(dq[r]) ) >= ( y(i) - y(dq[r]) ) * ( x(dq[r]) - x(dq[r-1]) ) ) r--; //维护凸壳
/*
这边取等号是因为 ti 可以=0,也就是会出现横坐标相同的两个点,那么有可能出现原先的斜率是 inf(即与 x 轴垂直,但是后面那个在前面那个上面),
加进来一个后变成 -inf,但它们的斜率表示出来是一样,如果不把前面那个弹掉,就不满足斜率单调递增了。
*/
dq[++r]=i;
}
printf("%lld\n",f[n]);
return 0;
}
50.忘情
把式子变成 $((\sum_{i=1}^n x_i)+1)^2 $,设 \(S\) 为前缀和,那么朴素的 dp 是:
设 \(f[i][j]\) 表示前 \(i\) 个数划分成 \(j\) 段的最小值,转移为 \(f[i][j]=\min_{0<=k<i}(f[k][j-1] + (S_i - S_j + 1)^2)\)。
容易证明 \((a+b+1)^2 > (a+1)^2 + (b+1)^2\),也就是说分的段数越多答案越小,即按照上面的定义 \(g(x)\) 表示分 \(x\) 段的最小值,那么 \(g(x)\) 的图像应该是一个下凸壳:
二分一个斜率 \(K\),用斜率 \(K\) 的直线去切这个凸包,那么截距 \(b=h(x)=g(x)-Kx\),因为是下凸包,所以我们要求最小截距,即把一段的权值定义成 \(((\sum xi)+1)^2 - K\),然后去掉段数限制,求最小答案。
考虑对这个新的问题 \(dp\),设 \(dp[i]\) 表示前 \(i\) 个数的最小值,\(dp[i]=\min_{0<=j<i}(dp[j] + (S[i]-S[j]+1)^2 - K)\),因为还要求此时的横坐标 \(x\),所以还要额外记一个dp数组,转移也是显然的。
这是经典的斜率优化形式,可以用单调队列优化到 \(O(n)\)。
总时间复杂度 \(O(n \log n)\)。
wqs 二分一些实现的细节:
- 这里因为是下凸包,所以斜率 \(K\) 是负的,但是为了方便二分时我们把他变成正的,所以 check 里 dp 变成 \(dp[i]=\min_{0<=j<i}(dp[j] + (S[i]-S[j]+1)^2 + K)\) , 原来二分要把斜率调大的就调小。
- 注意最后凸包可能会有一段斜率为 \(0\) 的线段,即可能 \(g(m-1)=g(m)\),那如果我们在 \(check\) 里的斜率优化dp,在 \(g\) 值相同时取的是靠左的点,那么二分写的就是: 如果返回的那个 \(x\) <=m,那就更新答案并把斜率调大(这里还认为斜率是负的,不进行 1. 的转换) ; 相反,如果我们在 \(check\) 里的斜率优化dp,在 \(g\) 值相同时取的是靠右的点,那么二分写的就是: 如果返回的那个 \(x\) >=m,那就更新答案并把斜率调小。看取的是靠左还是靠右只要看斜率优化维护凸包时写的是
>=还是>,>就是取靠左的,>=就是取靠右的。
code
变量名稍有不同。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5,inf=1e18;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,m,a[N];
int dp[N],g[N]; //dp[i]表示前 i 个数分成若干段的最小值,g[i] 表示取到最小值分的段树
int dq[N],l,r;
int calc(int j){ //求纵坐标
return dp[j]+a[j]*a[j]-2ll*a[j];
}
void check(int mid){
l=1,r=0;
dp[0]=0,g[0]=0;
dq[++r]=0; //放 0 不是 1,因为可以自成 1 段。
for(int i=1;i<=n;i++){
while(l<r && ( calc(dq[l+1]) - calc(dq[l]) ) < (2ll * a[i] * (a[dq[l+1]] - a[dq[l]]))) l++; //把开头斜率小于当前斜率的线段 pop 掉
int j=dq[l];
dp[i]=dp[j]+(a[i]-a[j]+1ll)*(a[i]-a[j]+1ll)+mid;
g[i]=g[j]+1ll;
while(l<r && ( calc(i) - calc(dq[r]) ) * ( a[dq[r]] - a[dq[r-1]]) < ( calc(dq[r]) - calc(dq[r-1] ) ) * ( a[i] - a[dq[r]] )) r--; //维护凸壳
dq[++r]=i;
}
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++) a[i]=read(),a[i]+=a[i-1];
int l=0,r=inf,mid,ans=0; //实际上斜率是负的,但是移项之后:b=f(x)-kx,所以就干脆把 k 取成正的,这样在check里是每一段+mid,而不是-mid
while(l<=r){
mid=(l+r)>>1;
check(mid);
if(g[n]<=m) r=mid-1,ans=mid;
else l=mid+1;
}
check(ans);
printf("%lld\n",dp[n]-ans*m); //这里要减掉 mid(也就是最后的 ans) 带来的贡献
return 0;
}
51.CF229D Towers
题意简化:
把一个序列分成若干段,使每一段的和非严格单增,求合并的最小操作数。
\(f[i]\) 表示前 \(i\) 个数的最少操作数,\(g[i]\) 表示此时最后一段的和。
下面 \(pre\) 表示前缀和。
容易发现最后一段的和越少越好,则
$f[i]_{0<=j<i,g[j]<=pre[i]-pre[j]}=f[j]+i-j-1 $, 即把 \([j+1,i]\) 分为一段,最后一个满足条件的 \(j\) 就是我们要的,因为此时最后一段的和 \(pre[i]-pre[j]\) 最小。
这个紫题是不是有点水了。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,a[N],f[N],g[N];
signed main(){
n=read();
for(int i=1;i<=n;i++) a[i]=read(),a[i]+=a[i-1];
f[0]=0,g[0]=0;
for(int i=1;i<=n;i++){
for(int j=i-1;j>=0;j--){
if(g[j]<=a[i]-a[j]){
f[i]=f[j]+i-j-1;
g[i]=a[i]-a[j];
break;
}
}
}
printf("%d\n",f[n]);
return 0;
}
52.【模板】"动态 DP"&动态树分治
也可见博客DP优化——动态dp。
这道题是简单版。
简单版的前置知识:树链剖分,广义矩阵乘法。
不带修改的话,最大权独立集很简单:
\(f[u][0] = \sum _{v\in son(u)}max(f[v][0],f[v][1])\),表示不选 u 的答案。
\(f[u][1] = w[u] + \sum _{v\in son(u)}f[v][0]\),表示选 u 的答案。
注意到我们更改一个点的点权其实只会修改他到根的链上的那些 \(dp\) 值,所以全部重算一点都不划算。
考虑只去更改这条链上的dp值。
但这样当树是链时还是有可能 TLE (虽然题解区似乎有人 \(n\) 方过百万),这个时候就会想到树链剖分。
因为根到一个点最多会有 log 个不同的重链,所以可以考虑重链之间暴力修改,重链上用线段树快速维护。
这样的话我们就需要更改一下 \(f\) 的转移,使得能与树剖的性质匹配(\(f\) 的定义不变)。
设 \(g[u][0/1]\) 表述 \(u\) 选/不选,只考虑 \(u\) 的那些轻儿子,的答案。
那么 (\(son[u]\) 表示 \(u\) 的重儿子):
\(f[u][0] = g[u][0] + max(f[son[u][0],f[son[u][1])\)
\(f[u][1] = g[u][1] + f[son[u]][0]\)。
特别的,叶子结点的 \(g[u][0]=0,g[u][1]=w[u]\) (和他的 f 相同)。
因为没了讨厌的 \(∑\),这个转移我们尝试改写成矩阵(为了后面用线段树维护)。
\(f[u][0] = max(g[u][0]+f[son[u][0] , g[u][0]+f[son[u]][1])\)
\(f[u][1] = g[u][1] + f[son[u]][0]\)。
根据这个可以得到他的矩阵形式,其中 max 是矩乘的+,+是矩乘的*。
会得到转移矩阵里只跟当前点的 \(g\) 有关。
注意到转移时我们只需要重儿子的信息,以及当前点的 \(g\) 值,所以我们在线段树上维护每个点的 \(g\) 所构成的转移矩阵以及矩阵的区间乘积。
又注意到一条重链的底部一定是叶子。
所以对于一条重链的顶端他的 \(f\) 值就是这条重链的每个转移矩阵的乘积再乘一个初始矩阵(就是叶子的 \(f\) 值),这个区间乘线段树是好维护的。
所以我们只维护 \(g\) (或者其实是转移矩阵)就可以了。
修改流程如下:
- 当修改一个点 \(u\) 的点权时,当前点的 \(g[u][1]\) 要变一下。
- 然后 \(u\) 到 \(top[u](重链顶端)\) 的所有点的 \(g\) 都是不变的,因为 \(g\) 在计算时不包含重儿子。
- 当 \(top[u]\) 跳到 \(fa[top[u]]\) 时,这时因为 \(top[u]\) 是 \(fa[top[u]]\) 的轻儿子,所以要更改 \(fa[top[u]]\) 的 \(g\) 值。
算 \(fa[top[u]\) 的 \(g\) 值要用到 \(top[u]\) 的 \(f\) 值,所以这个时候需要在线段树上区间查询一下。
复杂度是 \(O(n\times log^2(n))\),因为修改时要跳 \(log\) 次,每跳一次都要在线段树上查询一次。
一些细节:
矩阵乘法不满足交换律!!!所以线段树上 pushup 要从后往前合并。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
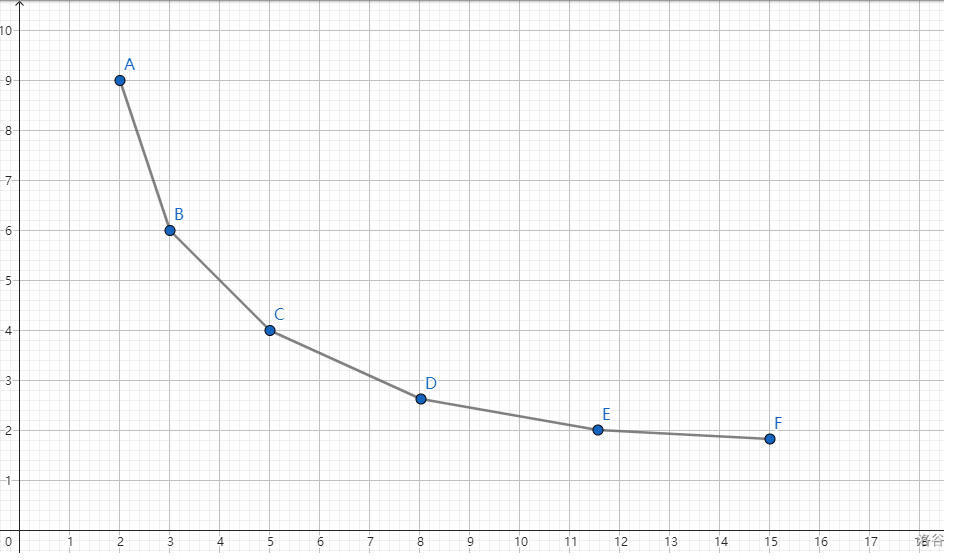
return s * w;
}
int n,T,w[N];
int tot,head[N],to[N<<1],Next[N<<1];
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
int top[N],down[N],rev[N],dfn[N],fa[N],son[N],Size[N],num,g[N][2],f[N][2];
//down是重链底端
void dfs1(int u){
Size[u]=1;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa[u]) continue;
fa[v]=u;
dfs1(v);
Size[u]+=Size[v];
if(Size[v]>Size[son[u]]) son[u]=v;
}
}
void dfs2(int u){
dfn[u]=++num;
rev[num]=u;
if(son[fa[u]]==u) top[u]=top[fa[u]];
else top[u]=u;
if(son[u]) dfs2(son[u]),down[u]=down[son[u]];
else down[u]=u;
g[u][1]=w[u];
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa[u]||v==son[u]) continue;
dfs2(v);
g[u][0]+=max(f[v][0],f[v][1]);
g[u][1]+=f[v][0];
}
f[u][0]=g[u][0]+max(f[son[u]][0],f[son[u]][1]);
f[u][1]=g[u][1]+f[son[u]][0];
}
struct Matrix{
int n,m,a[3][3];
void Init(){memset(a,-0x3f,sizeof a);}
void Init2(){ //单位矩阵
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
if(i==j) a[i][j]=0;
else a[i][j]=-0x3f3f3f3f;
}
}
}
}F;
Matrix operator *(Matrix A,Matrix B){
Matrix C; C.Init();
C.n=A.n,C.m=B.m;
for(int i=1;i<=C.n;i++){
for(int j=1;j<=C.m;j++){
for(int k=1;k<=A.m;k++){
C.a[i][j]=max(C.a[i][j],A.a[i][k]+B.a[k][j]);
}
}
}
return C;
}
struct node{
int l,r;
Matrix G;
};
struct SegmentTree{
node t[N<<2];
void pushup(int p){
t[p].G=t[p<<1|1].G*t[p<<1].G;
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r;
if(l==r){
t[p].G.n=2,t[p].G.m=2;
int u=rev[l];
t[p].G.a[1][1]=g[u][0],t[p].G.a[1][2]=g[u][1],t[p].G.a[2][1]=g[u][0],t[p].G.a[2][2]=-0x3f3f3f3f;
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
pushup(p);
}
void change(int p,int x){
if(t[p].l==t[p].r){
int u=rev[x];
t[p].G.a[1][1]=g[u][0],t[p].G.a[1][2]=g[u][1],t[p].G.a[2][1]=g[u][0],t[p].G.a[2][2]=-0x3f3f3f3f;
return;
}
int mid=(t[p].l+t[p].r)>>1;
if(x<=mid) change(p<<1,x);
else change(p<<1|1,x);
pushup(p);
}
Matrix ask(int p,int l,int r){
if(l<=t[p].l&&t[p].r<=r) return t[p].G;
int mid=(t[p].l+t[p].r)>>1;
Matrix Res; Res.n=2,Res.m=2,Res.Init2();
if(r>mid) Res=Res*ask(p<<1|1,l,r);
if(l<=mid) Res=Res*ask(p<<1,l,r);
return Res;
}
}Seg;
void Init(){ //预处理:树剖,g 数组,f 数组,初始化线段树
dfs1(1);
dfs2(1);
Seg.build(1,1,n);
F.n=1,F.m=2;
F.a[1][1]=0,F.a[1][2]=-0x3f3f3f3f; //初始矩阵,F 乘以叶子的转移矩阵就是叶子的 f。
}
void change(int x,int y){
int tmp=x;
x=top[x];
while(x!=1){ //先算出涉及到的点原来的 f
Matrix Ans=F;
Ans=Ans * Seg.ask(1,dfn[x],dfn[down[x]]);
f[x][0]=Ans.a[1][1],f[x][1]=Ans.a[1][2];
g[ fa[x] ][0] -= max(f[x][0],f[x][1]);
g[ fa[x] ][1] -= f[x][0];
x=top[fa[x]];
}
x=tmp;
g[x][1]-=w[x] , w[x]=y , g[x][1]+=w[x];
Seg.change(1,dfn[x]);
x=top[x];
while(x!=1){
Matrix Ans=F;
Ans=Ans * Seg.ask(1,dfn[x],dfn[down[x]]);
f[x][0]=Ans.a[1][1],f[x][1]=Ans.a[1][2];
g[ fa[x] ][0] += max(f[x][0],f[x][1]);
g[ fa[x] ][1] += f[x][0];
Seg.change(1,dfn[fa[x]]);
x=top[fa[x]];
}
}
signed main(){
// freopen(".in","r",stdin);
// freopen(".out","w",stdout);
n=read(),T=read();
for(int i=1;i<=n;i++) w[i]=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v),add(v,u);
}
Init();
while(T--){
int x=read(),y=read();
change(x,y);
Matrix Ans=F;
Ans=Ans * Seg.ask(1,dfn[1],dfn[down[1]]);
printf("%d\n",max(Ans.a[1][1],Ans.a[1][2]));
}
return 0;
}
53.【模板】"动态DP"&动态树分治(加强版)
把树剖卡掉了。
那有什么别的办法呢?
于是就诞生了这个非常厉害的科技——全局平衡二叉树。
请确保先会了简单版的树剖 + 线段树写法。
思考树剖为什么需要两个 \(\log\),因为我们每往上跳一次就要做一次 \(O(\log n)\) 的区间查询,然后我们一共要跳 \(\log\) 次,所以是两个 \(\log\)。
考虑把一个 \(\log\) 去掉,跳 \(\log\) 次重链的这个 \(\log\) 肯定是去不掉了,只能去掉那个查询的 \(\log\)。
但是很难有一个数据结构能 \(O(1)\) 维护一个比较复杂的且带修的区间信息。
所以全局平衡二叉树的主要思路就是使树高直接变成 \(\log\),然后每一次真的直接往上一步步跳,而不是跳一条重链,在跳的过程中上传信息并合并(这个容易做到 \(O(1)\)),这样每次跳都是 \(O(1)\) 的了。
怎么建树呢?
- 首先全局平衡二叉树先对每条重链建了一个平衡二叉树,每条重链的建法是:
- 先一遍 dfs 维护出基本信息 \(Size\) 表示子树大小,\(son\) 表示重儿子,\(lsiz\) 表示除去重儿子所在子树的子树大小。
- 然后对每条重链弄一个类似点分治的过程,把这条链搞到一段序列上,每次找出以 \(lsiz\) 为权值的带权中点 \(rt\);
以 \(rt\) 为平衡二叉树的根,然后左右分别递归建树并把左右两边得到的根设为 \(rt\) 的左右儿子。
- 然后把一个点用轻边连接的儿子对应的平衡二叉树的根接到这个点对应的平衡二叉树的根下面。
举个例子,比如这个图:
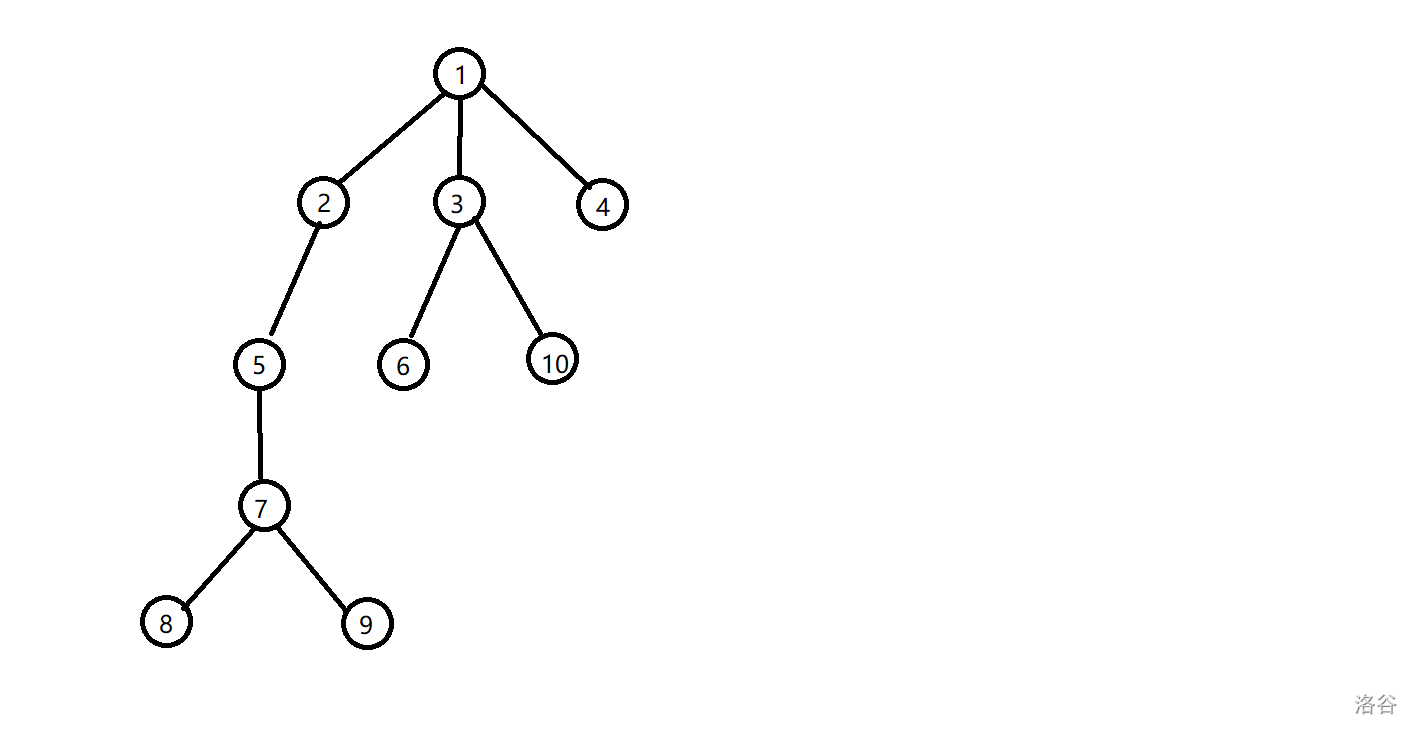
他的重链以及 \(lsiz\) 如下图所示:
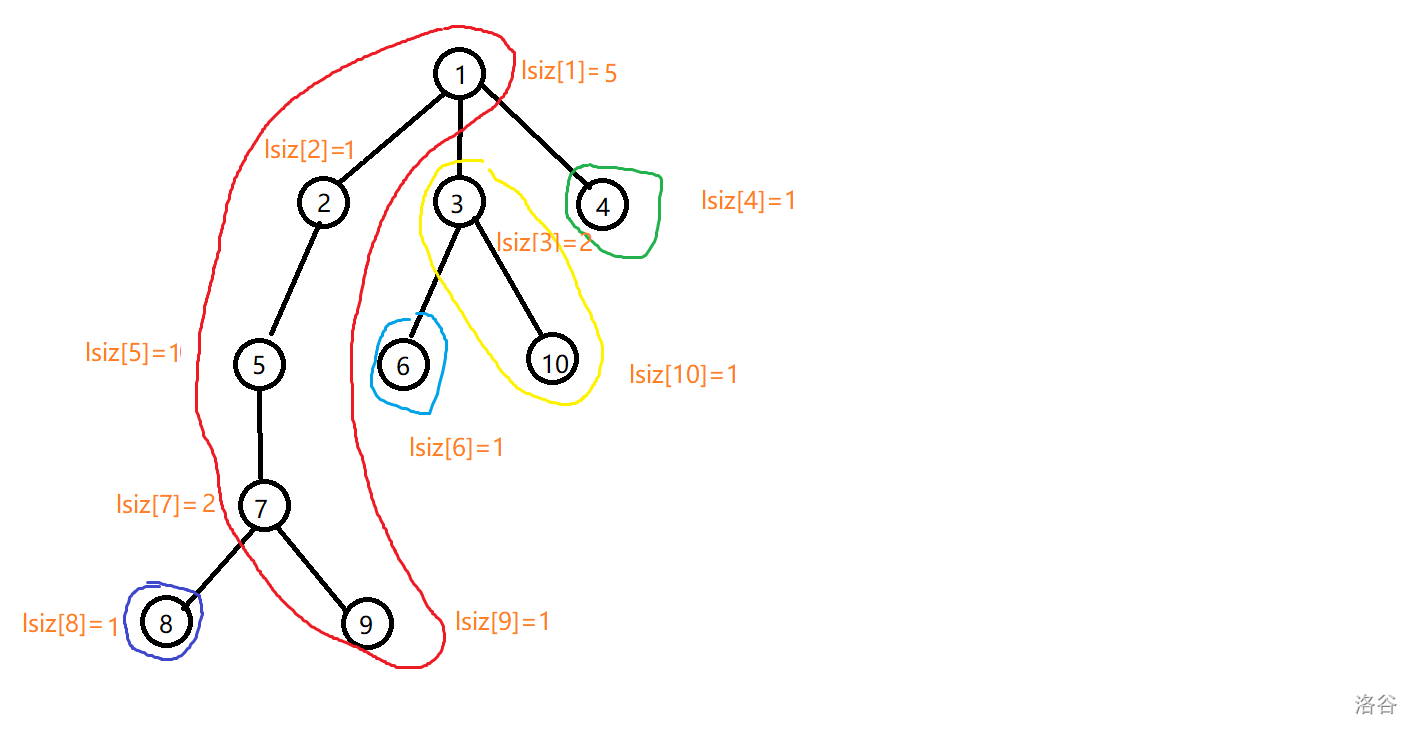
那么他建出的全局平衡二叉树应该长这样子,不同颜色代表不同重链建出的平衡二叉树,虚线边代表连接这些二叉树的边:

Tip:所以可以看出全局平衡二叉树并不是一棵二叉树,而是一个二叉树森林连接起来得到的一棵多叉树。
思路就是这么个思路,代码实现时:
递归建树,当 build 到一个点 \(u\) 时,先拉出重链,
然后对重链上的每个点先去递归它的轻儿子并把返回的根接到那个点上(对于轻边我们只记录父亲而不记录儿子)。
对于一条重链再按照上面所说的方法去特殊地建树,
并维护出这个重链的所有转移矩阵的乘积,只要每次 pushup 即可,还是记得注意顺序,因为矩阵乘法没有交换律。
到此全局平衡二叉树就建完了。
全局平衡二叉树的每个点维护了两个信息,自己这个点本身的转移矩阵 \(matr1\),他所代表的重链上的区间的转移矩阵的乘积 \(matr2\)。
修改时,我们从修改的点开始,先改掉它对应的转移矩阵 \(matr1\) (此时先不要 pushup 更改自身的 \(matr2\),因为后面需要用到旧的 \(matr2\))。
然后在全局平衡二叉树上一步一步往上跳,假设当前在 \(u\) 点,全局平衡二叉树上的父亲为 \(fa\):
- 如果 \((u,fa)\) 这条边是重边就直接
pushup(u)把 \(u\) 的 \(matr2\) 改掉,先不用修改 \(fa\) 的 \(matr2\); - 如果 \((u,fa)\) 这条边是轻边,此时 \(u\) 的 \(matr2\) 是旧版本,可以很快的求出 \(u\) 原先的 \(f\) 值,把 \(fa\) 的转移矩阵 \(matr1\) 减掉旧的 \(f\) 值;再
pushup(u),算出新的 \(f\) 值,把 \(fa\) 的转移矩阵 \(matr1\) 加上新的 \(f\) 值。
查询时,如果查询根的话,直接查询根所在重链的转移矩阵的乘积即可。
查询子树的话,我们需要的是原树上查询点 \(u\) 到其所在重链底端的所有矩阵的乘积,从全局平衡二叉树的 \(u\) 点开始,下面 \(treefa[u]\) 表示 \(u\) 在全局平衡二叉树上的父亲。
- 把自身节点的 \(matr1\) 以及右儿子的 \(matr2\) 统计入答案。
- 如果 \(u\) 是父亲 \(treefa[u]\) 的左儿子,那么需要把父亲的 \(matr1\) 以及父亲的右儿子的 \(matr2\) 统计上;否则这一步不进行操作。
- 跳到父亲。
- 重复执行 2~3 步直到跳到根。
比如有一条有 \(12\) 个点的重链,它们对应到区间上长这样:

把他特殊建出的平衡二叉树长这样(圈出的点是每一层的根,只圈出了需要用到的根):
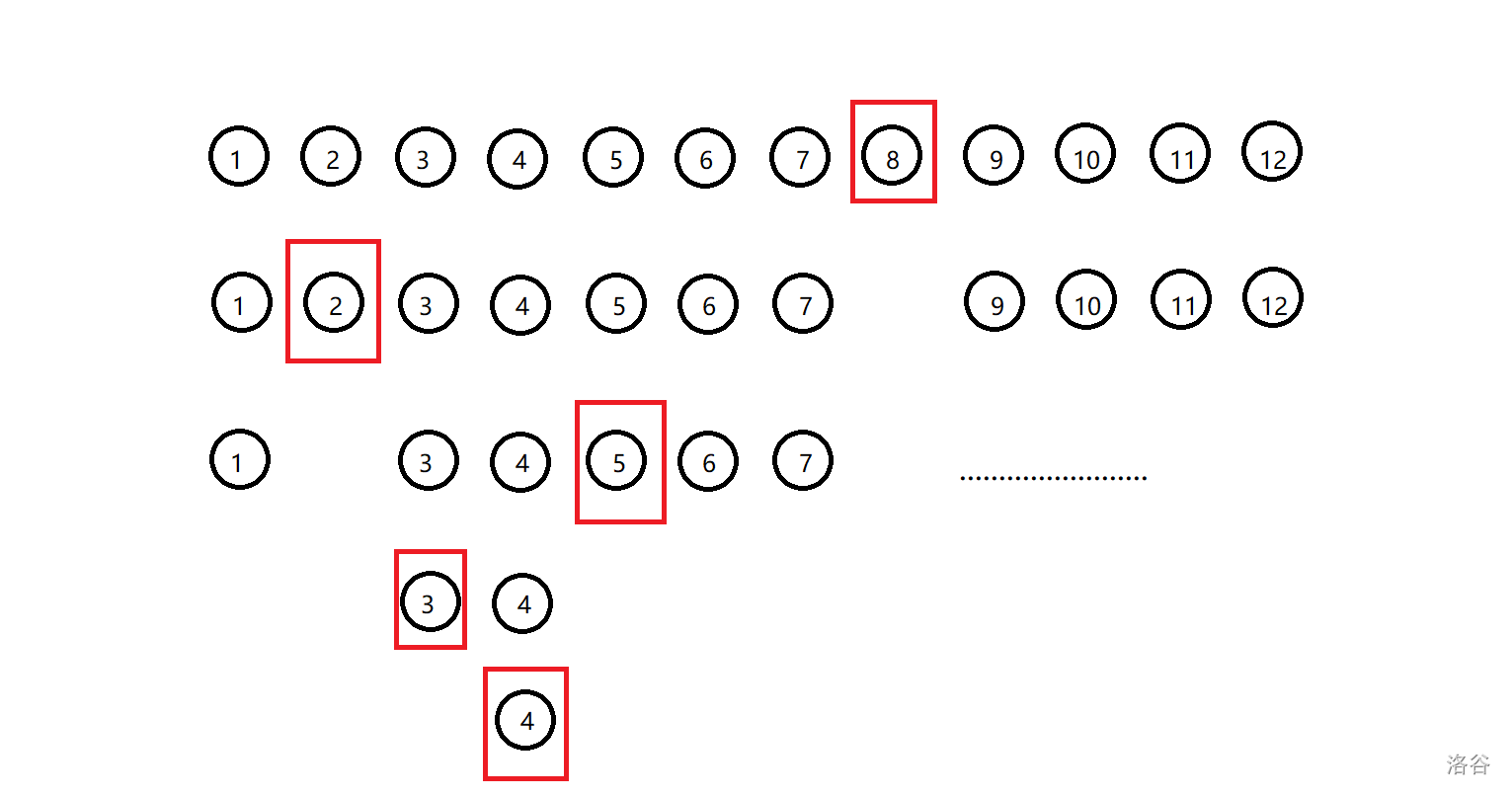
现在要查询 \(4\) 号点子树内的信息,就是查询区间 \([4,12]\) 内的点的转移矩阵的乘积。模拟上述过程如下:
- 将 \(4\) 号点自身的转移矩阵和右子树代表的区间(这个图里没有)的转移矩阵的乘积计入答案。
此时计入答案的点:\(4\)。 - 因为 \(4\) 号点是 \(3\) 号点的右儿子所以 \(3\) 号点不计入答案,然后跳到 \(3\) 号点。
此时计入答案的点:\(4\)。 - \(3\) 号点是 \(5\) 号点的左儿子,所以 \(5\) 号点以及 \(5\) 号点的右子树代表的区间 \([6,7]\) 计入答案,并跳到 \(5\) 号点。
此时计入答案的点:\(4,5,6,7\)。 - \(5\) 号点是 \(2\) 号点的右儿子,不操作,并跳到 \(2\) 号点。
此时计入答案的点:\(4,5,6,7\)。 - \(2\) 号点是 \(8\) 号点的左儿子,将 \(8\) 号点,以及右子树区间 \([9,12]\) 计入答案。并跳到 \(8\) 号点。
此时计入答案的点:\(4,5,6,7,8,9,10,11,12\)。 - 跳到根了,结束。
查询子树的复杂度为 \(O(\log n)\)。
时间复杂度分析:
- 如果往下的边是轻边,每一次子树大小减少一半,所以至多走 \(O(\log n)\) 条轻边;
- 如果往下的边是重边,因为重边特殊的建法,每一次取带权中点,子树大小也减半,所以至多走 \(O(\log n)\) 条重边。
所以树高是 \(O(\log n)\) 的。
一些细节见代码,个人认为码量和树剖差不多。
code
#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=1e6+5,inf=0x3f3f3f3f;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,T,w[N];
int tot,head[N],to[N<<1],Next[N<<1];
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
int son[N],Size[N],lsiz[N],g[N][2],f[N][2];
void dfs1(int u,int fa){
Size[u]=1;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa) continue;
dfs1(v,u);
Size[u]+=Size[v];
if(Size[v]>Size[son[u]]) son[u]=v;
}
lsiz[u]=Size[u]-Size[son[u]];
}
void dfs2(int u,int fa){
if(son[u]) dfs2(son[u],u);
g[u][1]=w[u];
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==fa||v==son[u]) continue;
dfs2(v,u);
g[u][0]+=max(f[v][0],f[v][1]);
g[u][1]+=f[v][0];
}
f[u][0]=g[u][0]+max(f[son[u]][0],f[son[u]][1]);
f[u][1]=g[u][1]+f[son[u]][0];
}
struct Matrix{
int n,m,a[2][2];
void Init(){memset(a,-0x3f,sizeof a);}
}F;
Matrix operator *(Matrix A,Matrix B){
Matrix C; C.Init();
C.n=A.n,C.m=B.m;
for(int i=0;i<=C.n;i++){
for(int j=0;j<=C.m;j++){
for(int k=0;k<=A.m;k++){
C.a[i][j]=max(C.a[i][j],A.a[i][k]+B.a[k][j]);
}
}
}
return C;
}
struct Tree{
int ls,rs;
Matrix matr1,matr2;
}t[N];
void pushup(int p){
t[p].matr2=t[p].matr1;
//还是注意要从右往左合并,因为这个调了一个上午。
if(t[p].rs) t[p].matr2 = t[ t[p].rs ].matr2 * t[p].matr2;
if(t[p].ls) t[p].matr2 = t[p].matr2 * t[ t[p].ls ].matr2; //注意顺序
}
PII Getf(int p){ //得到此时 p 点的 matr2*F 的值(注意这个不一定是 p 点在原树上的 f 值,因为 matr2 不一定是原树上 p 到重链底端的所有转移矩阵的乘积)
Matrix Ans=F*t[p].matr2;
return {Ans.a[0][0],Ans.a[0][1]};
}
int treefa[N],root;
bool vis[N];
int st[N],top;
int SBuild(int l,int r){ //对重链特殊建树
if(l>r) return 0;
int sum=0;
for(int i=l;i<=r;i++) sum+=lsiz[st[i]];
for(int i=l,s=lsiz[st[l]];i<=r;i++,s+=lsiz[st[i]]){
if(s * 2 >= sum){ //带权中点
int p=st[i],lson=SBuild(l,i-1),rson=SBuild(i+1,r);
t[p].ls=lson,t[p].rs=rson;
treefa[lson]=treefa[rson]=p;
pushup(p);
return p;
}
}
return 0;
}
int Build(int u){
for(int x=u;x;x=son[x]) vis[x]=true;
for(int x=u;x;x=son[x]){
for(int i=head[x];i;i=Next[i]){ //先递归轻儿子
int y=to[i];
if(vis[y]) continue;
treefa[Build(y)]=x;
}
}
top=0; //因为 top 是全局变量,所以不能写在vis那里,不然在上面递归到 y 时就被覆盖了!!!
for(int x=u;x;x=son[x]) st[++top]=x;
return SBuild(1,top);
}
void Init(){ //预处理除了建树都和树剖写法一样
dfs1(1,0);
dfs2(1,0);
for(int x=1;x<=n;x++){
t[x].matr1.n=1,t[x].matr1.m=1;
t[x].matr1.a[0][0]=g[x][0],t[x].matr1.a[0][1]=g[x][1];
t[x].matr1.a[1][0]=g[x][0],t[x].matr1.a[1][1]=-inf;
}
F.n=0,F.m=1;
F.a[0][0]=0,F.a[0][1]=-inf;
root=Build(1);
}
void change(int u,int val){
t[u].matr1.a[0][1]+=val-w[u];
w[u]=val;
for(;u;u=treefa[u]){ //这里不能写 for(;u!=root;u=treefa[u]) 因为这样的话根的 matr2 没有被 pushup 更新。
int fa=treefa[u];
if(fa && t[fa].ls !=u && t[fa].rs != u){ //轻边
PII oldf=Getf(u);
t[fa].matr1.a[0][0] -= max(oldf.fi , oldf.se) ;
t[fa].matr1.a[0][1] -= oldf.fi ;
t[fa].matr1.a[1][0] -= max(oldf.fi , oldf.se) ;
pushup(u);
PII newf=Getf(u);
t[fa].matr1.a[0][0] += max(newf.fi , newf.se) ;
t[fa].matr1.a[0][1] += newf.fi ;
t[fa].matr1.a[1][0] += max(newf.fi , newf.se) ;
}
else pushup(u);
}
}
signed main(){
// freopen("P4751_4.in","r",stdin);
// freopen(".out","w",stdout);
n=read(),T=read();
for(int i=1;i<=n;i++) w[i]=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v),add(v,u);
}
Init();
int lstans=0;
while(T--){
int x=read()^lstans,y=read();
change(x,y);
PII ans=Getf(root);
lstans = max(ans.fi,ans.se);
printf("%d\n",lstans);
}
return 0;
}
参考网址:动态DP之全局平衡二叉树
54. CF1603D Artistic Partition
题意就是让你把序列分成 \(k\) 段,使每一段的 \(c\) 值的和尽可能小。
设 \(f[i][k]\) 表示前 \(i\) 个数,分成 \(k\) 段的最小值,则:
\(f[i][k] = \min_{1\le j \le i}(f[j-1][k-1]+c(j,i))\)。
注意到这个状态直接爆了,但我们会发现因为 \(c(l,r)\ge r-l+1\),所以 \(f[n][k]\ge n\)。
而 \(f(l,2l-1)=(2l-1)-l+1\),即 \(r<2l\) 时 \(f(l,r)=r-l+1\),所以如果我们分出的 \(k\) 段是:
\([1,1],[2,3],[4,7],...,[2^{k-1},2^k-1]\)
时,每段区间的 \(c(l,r)\) 的和刚好 \(=n\),即如果 \(2^k-1\ge n\),答案是 \(n\),所以我们需要考虑的 \(k\) 就是 \(\log n\) 级别的,但这样仅仅是把状态优化了,时间复杂度照爆不误。
直接暴力化简 \(c(l,r)\):
\[\begin{aligned} c(l,r) &= \sum_{i=l}^r\sum_{j=i}^r [gcd(i,j)\ge l] \\ &= \sum_{k=l}^r\sum_{i=l}^r\sum_{j=i}^r [gcd(i,j)=k] \\ &= \sum_{k=l}^r\sum_{i=\lfloor \frac{l}{k} \rfloor}^{\lfloor \frac{r}{k} \rfloor }\sum_{j=i}^{\lfloor \frac{r}{k} \rfloor } [gcd(i,j)=k] \\ &= \sum_{k=l}^r\sum_{i=\lfloor \frac{l}{k} \rfloor}^{\lfloor \frac{r}{k} \rfloor }\sum_{j=i}^{\lfloor \frac{r}{k} \rfloor } [gcd(i,j)=1] \\ &= \sum_{k=l}^r\sum_{j=\lfloor \frac{l}{k} \rfloor}^{\lfloor \frac{r}{k} \rfloor }\sum_{i=\lfloor \frac{l}{k} \rfloor}^{j} [gcd(i,j)=1]\\ &= \sum_{k=l}^r\sum_{j=1}^{\lfloor \frac{r}{k} \rfloor }\sum_{i=1}^{j} [gcd(i,j)=1]\\ &= \sum_{k=l}^r\sum_{j=1}^{\lfloor \frac{r}{k} \rfloor } \varphi(j)\\ &= \sum_{k=l}^r s(\lfloor\frac{r}{k} \rfloor)\\ \end{aligned} \]其中 \(s(i)\) 表示 1~i 的欧拉函数的和,\(s\) 是可以预处理的。
盲猜一波 \(c(l,r)\) 满足四边形不等式,那就可以决策单调性优化了。
证明(来自题解区大佬):
设 \(f(l,p,r)=\sum_{k=l}^r s(\lfloor\frac{p}{k} \rfloor)\)。
对于 \(l_1\le l_2\le r_1\le r_2\),我们有:
那明显这个 \(f(l_1,r_2,l_2-1) - f(l_1,r_1,l_2-1) > 0\),所以 \(c(l,r)\) 满足四边形不等式。
这里采用分治优化复杂度,枚举 \(k\) 是 O\((\log n)\),一共 \(O(\log n)\) 层, 每一层转移 \(O(n)\),总时间复杂度 \(O(n\log^2n)\),为了每一层的复杂度严格 \(O(n)\),我们要支持 \(O(1)\) 查询 \(c(l,r)\)。
在更新 \(f[mid][k]\) 时,先用数论分块加上 \(c(\min(mid,R)+1,mid)\) , 再倒叙枚举 \(j\),然后每一次加入一个 \(s[mid/j]\) 即可。
如果没有数论分块算 \(c(\min(mid,R)+1,mid)\) 的复杂度,那时间复杂度是 \(O(n \log^2 n)\),加上这个就不太好算了。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int T,n,m;
int pri[N],cnt;
bool stater[N];
int mn[N],mx[N],phi[N];
void Eular(){
stater[1]=1;
phi[1]=1;
for(int i=2;i<N;i++){
if(!stater[i]) pri[++cnt]=i,mn[i]=i,mx[i]=i,phi[i]=i-1;
for(int j=1;j<=cnt&&i*pri[j]<N;j++){
int x=i*pri[j];
stater[x]=true;
mn[x]=pri[j];
if(i%pri[j]==0){
mx[x]=mx[i]*pri[j];
if(x!=mx[x]) phi[x]=phi[x/mx[x]]*phi[mx[x]];
else phi[x]=x/mn[x]*(mn[x]-1);
break;
}
else{
mx[x]=pri[j];
phi[x]=phi[i]*phi[pri[j]];
}
}
}
for(int i=1;i<N;i++){
phi[i]=phi[i-1]+phi[i];
}
}
int c(int l,int r){
int i=l,res=0;
while(i<=r){
int j=r/(r/i);
res+=(j-i+1)*phi[r/i];
i=j+1;
}
return res;
}
int f[N][20];
void solve(int k,int l,int r,int L,int R){
if(l>r) return;
int mid=(l+r)>>1,opt=-1,res=0;
int C=c(min(mid,R)+1,mid); //注意加上这个
for(int j=min(mid,R);j>=L;j--){
C+=phi[mid/j];
if(opt==-1 || f[j-1][k-1]+C<=res){
opt=j,res=f[j-1][k-1]+C;
}
}
f[mid][k]=res;
if(l>=r) return;
solve(k,l,mid,L,opt);
solve(k,mid+1,r,opt,R);
}
signed main(){
Eular();
T=read();
f[0][0]=0;
for(int i=1;i<N;i++) f[i][0]=0x3f3f3f3f3f3f3f3f;
for(int k=1;k<=18;k++)
solve(k,1,N-5,1,N-5);
while(T--){
n=read(),m=read();
if(m>20||(1<<m)>n){
printf("%lld\n",n);
continue;
}
printf("%lld\n",f[n][m]);
}
return 0;
55.CF1527E Partition Game
还是先看朴素 DP:
\(f[i][k]\) 表示前 \(i\) 个数分为 \(k\) 段的最小代价,则:\(f[i][k]=\min_{0\le j < i}{f[j][k-1]+cost(j+1,i)}\)
第一眼似乎这个 \(cost\) 完全无法优化求他的时间复杂度。
但是我们可以考虑 \(i\) 每次移一位后 \(cost\) 的变化:
对于 \(cost(j,i) \to cost(j,i+1)\),
- 如果 \(i\) 及以前最后一个 \(a[i+1]\) 的位置 \(lst_{a_{i+1}}\le j\),那么 \(cost(j,i+1)=cost(j,i)+(i+1)-lst_{a_{i+1}}\)
- 否则 \(cost(j,i+1)=cost(j,i)\)
所以这个式子 :
\(f[i][k]=\min_{0\le j < i}{f[j][k-1]+cost(j+1,i)}=\min_{0\le j < i}{g[j]}\)
和 \(i\) 变成 \(i+1\) 后的 :
\(f[i+1][k]=\min_{0\le j < i+1}{f[j][k-1]+cost(j+1,i+1)}=\min_{0\le j < i+1}{g[j]}\)。
只不过是把 \(0\le j<lst_{a_{i+1}}\) 的 \(g[j]\) 加上 \((i+1)-lst_{a_{i+1}}\),然后再加入一个 \(g[i]\) 就可以了。
线段树维护即可,\(O(k n \log n)\)。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=35000+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,k,a[N];
int lst[N],f[N][105];
struct node{
int l,r,ming,add;
void tag(int d){
ming+=d;
add+=d;
}
};
struct SegmentTree{
node t[N<<2];
void pushup(int p){
t[p].ming=min(t[p<<1].ming,t[p<<1|1].ming);
}
void spread(int p){
if(t[p].add){
t[p<<1].tag(t[p].add);
t[p<<1|1].tag(t[p].add);
t[p].add=0;
}
}
void build(int p,int l,int r){
t[p].l=l,t[p].r=r,t[p].add=0; //add也要清空
if(l==r){
t[p].ming=0;
return;
}
int mid=(l+r)>>1;
build(p<<1,l,mid);
build(p<<1|1,mid+1,r);
pushup(p);
}
void change(int p,int l,int r,int d){
if(l<=t[p].l&&t[p].r<=r){
t[p].tag(d);
return;
}
spread(p);
int mid=(t[p].l+t[p].r)>>1;
if(l<=mid) change(p<<1,l,r,d);
if(r>mid) change(p<<1|1,l,r,d);
pushup(p);
}
int ask(int p,int l,int r){
if(l<=t[p].l&&t[p].r<=r){
return t[p].ming;
}
int mid=(t[p].l+t[p].r)>>1,res=LLONG_MAX;
if(l<=mid) res=min(res,ask(p<<1,l,r));
if(r>mid) res=min(res,ask(p<<1|1,l,r));
return res;
}
}Seg;
signed main(){
n=read(),k=read();
for(int i=1;i<=n;i++) a[i]=read();
memset(f,0x3f,sizeof f);
f[0][0]=0;
for(int j=1;j<=k;j++){
Seg.build(1,0,n-1);
for(int i=1;i<=n;i++) lst[i]=0;
for(int i=1;i<=n;i++){
if(lst[a[i]]){
Seg.change(1,0,lst[a[i]]-1,i-lst[a[i]]);
}
Seg.change(1,i-1,i-1,f[i-1][j-1]); //cost(i,i)就省略了
lst[a[i]]=i;
f[i][j]=Seg.ask(1,0,i-1);
}
}
printf("%lld\n",f[n][k]);
return 0;
}
56.CF1476F Lanterns
比较考验思维,直接讲做法了。
\(f[i]\) 表示前 \(i\) 盏灯可以覆盖的最长前缀,转移:
- \(f[i-1]<i\),那可能 \(i\) 照的那一段就接不上 \(f[i-1]\) 了,\(f[i]=f[i-1]\)。
- \(f[i-1]\ge i\),那么 \(i\) 肯定往右照,\(f[i]=\max(f[i-1],i+p_i)\)。
- 存在一个 \(t\) (\(0\le t<i\)) ,虽然 \(f[t]<i\),但是 \(i\) 往左照后可以与它接起来,即满足 \(f[t]\ge i-p_i-1\),此时原先那些 \(t<j<i\),原先有可能无法被覆盖,现在他们肯定统一往右照最优,\(f[i]=\max(i-1 , \max_{t<j<i} (j+p_j))\)。(注意 \(i\) 自己照不到自己)。
因为有第一个转移,所以 \(f\) 肯定有单调性,二分出最靠左的 \(t\) (这样一定最优),进行转移 \(3\)。 后面的转移区间 RMQ 即可。
code
#include<bits/stdc++.h>
#define PII pair<int,int>
#define fi first
#define se second
using namespace std;
const int N=3e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int T,n,p[N],st[N][30];
int f[N];
PII from[N]; //第二维是1代表朝右,0代表超左
int RMQ(int l,int r){
if(l>r) return 0;
int k=log(r-l+1)/log(2);
return max(st[l][k],st[r-(1<<k)+1][k]);
}
void print(int u){
if(u==0||u==-1) return;
if(from[u].se){
print(from[u].fi);
putchar('R');
}
else{
print(from[u].fi);
for(int i=from[u].fi+1;i<=u-1;i++) putchar('R');
putchar('L');
}
}
signed main(){
T=read();
while(T--){
n=read();
for(int i=1;i<=n;i++) p[i]=read(),st[i][0]=i+p[i];
for(int t=1;t<=20;t++){
for(int i=1;i+(1<<t)-1<=n;i++){
st[i][t]=max(st[i][t-1],st[i+(1<<(t-1))][t-1]);
}
}
for(int i=1;i<=n;i++){
if(f[i-1]<i) f[i]=f[i-1],from[i]={-1,-1};
else f[i]=max(f[i-1],i+p[i]),from[i]={i-1,1};
int l=0,r=i-1,mid,t=-1;
while(l<=r){
int mid=(l+r)>>1;
if(f[mid]>=i-p[i]-1) t=mid,r=mid-1;
else l=mid+1;
}
if(t!=-1){
if(max(i-1,RMQ(t+1,i-1))>f[i]){
f[i]=max(i-1,RMQ(t+1,i-1));
from[i]={t,0};
}
}
}
if(f[n]<n) puts("NO");
else puts("YES"),print(n),puts("");
}
return 0;
}
57.划分(part)
因为是内部题,所以这个链接可能会挂,所以讲一下题意:
题意简述
对于一个正整数序列 \(a_i\),若它可以被划分为两个不相交的子序列(可以不连续,每个位置恰好属于其中
一个子序列),两个子序列的和相等,那么称这个序列为好序列。
对于一个正整数序列 ,若其所有长度为 \(k\) 的连续子序列都是好序列,那么称这个序列为 \(k-序列\)。
给你 个正整数序列,对于每个序列,求出它是 \(k-序列\) 的所有 \(k\) 的值。
数据范围:\(1\le n \le 10^3\),\(1\le \sum A_i \le 10^5\)。
题解
对于每个 \(k\),倒序枚举左端点,左端点往左移的时候用,\(f[s]\) 表示选出若干个和为 \(s\) 的数,右端点最靠左是多少(靠右显然不优),维护出 \(f\) 后再对每个 \(r\) 看一下是否有 \(sum \equiv 0\pmod 2 \land f[\frac{sum}{2}]<=r\),其中 \(sum=\sum_{i=l}^r a_i\)。
转移用背包即可,\(O(T n V)\)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5,M=1e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int T,n,a[N],pre[N];
bool flag[N];
int f[M];
vector<int> ans;
signed main(){
freopen("part.in","r",stdin);
freopen("part.out","w",stdout);
T=read();
while(T--){
n=read();
for(int i=1;i<=n;i++) a[i]=read(),pre[i]=pre[i-1]+a[i],flag[i]=true;
memset(f,0x3f,sizeof f);
for(int l=n;l>=1;l--){
for(int s=pre[n]/2;s>=a[l];s--) f[s]=min(f[s],f[s-a[l]]);
f[a[l]]=l;
for(int r=l;r<=n;r++){
int sum=pre[r]-pre[l-1];
if(sum%2==1) flag[r-l+1]=false;
else if(f[sum/2]>r) flag[r-l+1]=false;
}
}
ans.clear();
for(int i=1;i<=n;i++)
if(flag[i]) ans.push_back(i);
printf("%d ",ans.size());
for(int i=0;i<ans.size();i++){
if(i==ans.size()-1) printf("%d",ans[i]);
else printf("%d ",ans[i]);
}
puts("");
}
return 0;
}
58.超级马里奥(mario)
也是内部题,但是题面很长,直接贴图:

以下 \(c_i\) 统一已经对 \(C\) 取 \(\min\)。
注意到一个点上如果选择吃东西,那能量是直接赋值而不是累加。
所以如果枚举了哪些点要吃东西,那么任意相邻的两点之间就不能再补充能量了,能用的能量只跟上一个点的 \(c_i\) 有关。
设 \(d[i][j]\) 表示在 \(i\) 吃东西,走不超过 \(c_i\) 条边到 \(j\),最多能走的路程 (中间不再吃东西)。
我们先不考虑这东西怎么求,假设我们已经预处理出来了。
设 \(dp[sum][i]\) 表示起点在 \(i\) 号节点,有 \(sum\) 元钱,恰好用完,最多能走多少。
首先 \(i\) 号点是一定要吃东西的,不然没能量,考虑枚举下一个吃东西的点 \(j\),则 \(d[i][j]+dp[sum-p[i]][j] \to dp[sum][i]\),因为 \(q_i<=n^2\) 所以这个 dp 的复杂度是 \(O(n^4)\)。
回答询问时,先对它进行一次前缀 \(\max\) (就得到 "花不超过 \(sum\) 元钱能走的最长路线" ),然后二分求出需要花的最少钱数即可。
现在看 \(d[i][j]\) 的求法,考虑倍增优化 dp。
设 \(f[k][i][j]\) 表示从 \(i\) 开始,走不超过 \(2^k\) 条边,到 \(j\) 的最长路径。
转移时枚举中转点 \(u\),则 \(f[k-1][i][u]+f[k-1][u][j] \to f[k][i][j]\)。
这个 dp 的复杂度是 \(O(n^3 \log c_i)\)。
有了 \(f\) 来看怎么求 \(d\):
考虑对 \(c_i\) 做一个二进制拆分,设 \(c_i=2^{a_1}+2^{a_2}+...2^{a_k} (a_1>a_2>...>a_k)\)。
一开始 \(d[i][j]\) 仅仅表示从 \(i\) 开始,走不超过 \(0\) 条边,到 \(j\) 的最长路径,即除了 \(f[i][i]=0\),其余都是 \(-\infty\)。
我们现在要将它扩展到:从 \(i\) 开始,走不超过 \(2^{a_1}\) 条边,到 \(j\) 的最长路径:
那么枚举中转点 \(u\),所以有转移 \(d[i][u]+f[a1][u][j] \to d[i][j]\) , 为了防止用来转移的 \(d\) 数组已经被更新过了,可以先用辅助数组存一下。
这个过程非常像矩阵乘法,当然这里可以不写矩乘。如此不断扩展即可直到 \(d[i][j]\) 表示走不超过 \(2^{a_1}+2^{a_2}+...2^{a_k}\) 条边,到 \(j\) 的最长路径为止。
这个 dp 的复杂度是:
- 枚举 \(i\),\(O(n)\);
- 对每一个二进制位做一次扩展,\(O(\log c_i)\);
- 枚举 \(j\),\(O(n)\);
- 枚举 u,\(O(n)\)。
则这个 dp 的复杂度是 \(O(n^3 \log c_i)\)。
于是就写完了,图都不用建,注意重边只需要取最长的那一条。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e2+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,m,C,T;
int p[N],c[N],dist[N][N]; //dist:邻接矩阵
int f[20][N][N];
void DP_f(){
memset(f,-0x3f,sizeof f);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(i==j) f[0][i][j]=0;
else if(dist[i][j]) f[0][i][j]=dist[i][j];
for(int k=1;k<=18;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int u=1;u<=n;u++)
f[k][i][j]=max(f[k][i][j],f[k-1][i][u]+f[k-1][u][j]);
}
int d[N][N],tmp[N];
void DP_d(){
memset(d,-0x3f,sizeof d);
for(int i=1;i<=n;i++){
vector<int> a;
for(int j=18;j>=0;j--) if(c[i]>>j&1) a.push_back(j);
d[i][i]=0;
for(int k:a){
memset(tmp,-0x3f,sizeof tmp);
for(int j=1;j<=n;j++){
for(int u=1;u<=n;u++){
tmp[j]=max(tmp[j],d[i][u]+f[k][u][j]);
}
}
for(int j=1;j<=n;j++) d[i][j]=tmp[j];
}
}
}
int dp[N*N][N];
void DP_dp(){
memset(dp,-0x3f,sizeof dp);
for(int i=1;i<=n;i++) dp[0][i]=0;
for(int sum=1;sum<=n*n;sum++){
for(int i=1;i<=n;i++){
if(p[i]>sum) continue;
for(int j=1;j<=n;j++){
dp[sum][i]=max(dp[sum][i],d[i][j]+dp[sum-p[i]][j]);
}
}
}
}
signed main(){
freopen("mario.in","r",stdin);
freopen("mario.out","w",stdout);
n=read(),m=read(),C=read(),T=read();
for(int i=1;i<=n;i++){
p[i]=read(),c[i]=read();
c[i]=min(c[i],C);
}
for(int i=1;i<=m;i++){
int u=read(),v=read(),l=read();
dist[u][v]=max(dist[u][v],l);
}
DP_f();
DP_d();
DP_dp();
for(int i=1;i<=n;i++)
for(int sum=1;sum<=n*n;sum++)
dp[sum][i]=max(dp[sum-1][i],dp[sum][i]);
while(T--){
int s=read(),q=read(),d=read();
int l=0,r=q,mid,ans=-1;
while(l<=r){
mid=(l+r)>>1;
if(dp[mid][s]>=d) ans=mid,r=mid-1;
else l=mid+1;
}
if(ans==-1) puts("-1");
else printf("%lld\n",q-ans);
}
return 0;
}
59.CF685E Travelling Through the Snow Queen's Kingdom
CF685E Travelling Through the Snow Queen's Kingdom
这个故事告诉我们考场想出状态后不管会不会爆都要尝试一下...
设 \(f[i][x][y]\) 表示从第 \(i\) 天开始,要从 \(x\) 到 \(y\),到达时的最小日期,不行则 \(=m+1\)。
一开始 \(f[m+1][x][y]=m+1,f[i][x][x]=i\)。
当 \(i\) 从 \(i\) 变成 \(i-1\) 时,假设第 \(i\) 条边是 \((u,v)\)。
- 如果 \(x\neq u\) 且 \(x\neq v\) 那么这条边不会带来任何影响,因为 \(x\) 根本无法在 \(i\) 天之前走到 \(u/v\),\(f[i-1][x][y]=f[i][x][y]\)。
- 当 \(x=u\) 时,我可以选择走这条边,走过去之后时间变成 \(i\),那么 \(f[i-1][u][y]=\min(f[i][u][y],f[i][v][y]\)。
- 当 \(x=v\) 时同理。
倒叙处理天数并回答询问即可,时间复杂度 \(O(nm)\)。
考场我以为这个dp时间复杂度不对就没写...
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e3+5,M=2e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,m,u[M],v[M],q;
int f[N][N];
struct P{
int l,r,s,t,id;
};
vector<P> que[M];
bool ans[M];
signed main(){
freopen("plan.in","r",stdin);
freopen("plan.out","w",stdout);
n=read(),m=read(),q=read();
for(int i=1;i<=m;i++){
u[i]=read(),v[i]=read();
}
for(int i=1;i<=q;i++){
int l=read(),r=read(),s=read(),t=read();
que[l].push_back({l,r,s,t,i});
}
for(int x=1;x<=n;x++){
for(int y=1;y<=n;y++){
f[x][y]=m+1;
}
}
for(int i=m+1;i>=1;i--){
for(int x=1;x<=n;x++) f[x][x]=i;
for(int y=1;y<=n;y++)
f[u[i]][y]=min(f[u[i]][y],f[v[i]][y]);
for(int y=1;y<=n;y++)
f[v[i]][y]=min(f[v[i]][y],f[u[i]][y]);
for(P pro:que[i]){
ans[pro.id]=(f[pro.s][pro.t]<=pro.r);
}
}
for(int i=1;i<=q;i++)
if(ans[i]) puts("Yes");
else puts("No");
return 0;
}
60.CF1039D You Are Given a Tree
先考虑树形DP怎么求一个 \(k\) 的答案:
\(f[u]\) 表示 \(u\) 这棵子树内的答案,\(g[u]\) 表示如果 \(u\) 不在 \(f[u]\) 中的链里,\(u\) 往下的最长链是什么。
设 \(mx_1,mx_2\) 表示 \(u\) 的儿子 \(v\) 中 \(g[v]\) 的最大和次大值,那么先令 \(f[u]=\sum f[v]\),然后:
- 如果 \(mx_1+mx_2+1\ge k\):\(f[u]=f[u]+1,g[u]=0\)。
- \(g[u]=mx_1+1\);
容易发现答案单调不增,并且对于 \(\sqrt n \le k \le n\),有 \(1\le ans\le \sqrt n\)。
这启示我们根号分治,假设我们 \(1\le k<B\) 的 \(k\) 暴力树形DP,\(B\le k\le n\) 的 \(k\) 我们考虑二分:
枚举 \(ans\),二分出答案是 \(ans\) 的 \(k\) 的区间,我们只需要知道右端点就ok了。
二分的 check 就是跑一遍树形DP。
时间复杂度是:\(O(Bn+\frac{n^2}{B}\log n)\),\(B\) 应该取 \(\sqrt{n\log n}\) 。
然后如果你的根号分治 TLE 了,这里有个经典卡常技巧:把树搞成dfs序,然后倒着扫,就可以避免每一次dfs递归了。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,m;
int tot,head[N],to[N<<1],Next[N<<1];
void add(int u,int v){
to[++tot]=v,Next[tot]=head[u],head[u]=tot;
}
int fa[N],rev[N],num;
void DFS(int u,int Fa){
fa[u]=Fa;
rev[++num]=u; //把树拍成dfs序
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(v==Fa) continue;
DFS(v,u);
}
}
int f[N],g[N],mx1[N],mx2[N];
void dfs(int k){
for(int i=1;i<=n;i++) f[i]=g[i]=mx1[i]=mx2[i]=0;
for(int i=num;i>=1;i--){
int u=rev[i];
if(1+mx1[u]+mx2[u]>=k) f[u]++;
else g[u]=mx1[u]+1;
if(!fa[u]) continue;
f[fa[u]]+=f[u];
if(g[u]>mx1[fa[u]]) mx2[fa[u]]=mx1[fa[u]],mx1[fa[u]]=g[u];
else mx2[fa[u]]=max(mx2[fa[u]],g[u]);
}
}
bool check(int k,int ans){
dfs(k);
return f[1]>=ans;
}
signed main(){
n=read();
for(int i=1;i<n;i++){
int u=read(),v=read();
add(u,v),add(v,u);
}
DFS(1,0);
m=sqrt(n*log2(n));
for(int k=1;k<=m;k++){
dfs(k);
printf("%d\n",f[1]);
}
int lst=m+1;
for(int ans=n/m+1;ans>=0;ans--){
int l=lst,r=n,mid,res=-1;
while(l<=r){
mid=(l+r)>>1;
if(check(mid,ans)) l=mid+1,res=mid;
else r=mid-1;
}
if(res==-1) continue;
for(int k=lst;k<=res;k++) printf("%d\n",ans);
lst=res+1;
}
return 0;
}