BLOG—2

标签：getX get double ps BLOG getY public

一、前言

PTA题目集4（四边形）、5（五边形）以及期中考试的总结性Blog。本次考察了正则表达式的基本应用，利用正则表达式找到符合要求的字符，不同类的方法相互调用，以及数学逻辑思维。期中考试由浅入深地考察了封装、继承、多态等Java常见语法。

二、设计与分析

7-1 sdut-String-2 识蛟龙号载人深潜，立科技报国志（II）（正则表达式）

背景简介：

“蛟龙号”载人深潜器是我国首台自主设计、自主集成研制的作业型深海载人潜水器，设计最大下潜深度为7000米级，也是目前世界上下潜能力最强的作业型载人潜水器。“蛟龙号”可在占世界海洋面积99.8%的广阔海域中使用，对于我国开发利用深海的资源有着重要的意义。

中国是继美、法、俄、日之后世界上第五个掌握大深度载人深潜技术的国家。在全球载人潜水器中，“蛟龙号”属于第一梯队。目前全世界投入使用的各类载人潜水器约90艘，其中下潜深度超过1000米的仅有12艘，更深的潜水器数量更少，目前拥有6000米以上深度载人潜水器的国家包括中国、美国、日本、法国和俄罗斯。除中国外，其他4国的作业型载人潜水器最大工作深度为日本深潜器的6527米，因此“蛟龙号”载人潜水器在西太平洋的马里亚纳海沟海试成功到达7020米海底，创造了作业类载人潜水器新的世界纪录。

从2009年至2012年，蛟龙号接连取得1000米级、3000米级、5000米级和7000米级海试成功。下潜至7000米，说明蛟龙号载人潜水器集成技术的成熟，标志着我国深海潜水器成为海洋科学考察的前沿与制高点之一。

2012年6月27日11时47分，中国“蛟龙”再次刷新“中国深度”——下潜7062米。6月3日，“蛟龙”出征以来，已经连续书写了5个“中国深度”新纪录：6月15日，6671米；6月19日，6965米；6月22日，6963米；6月24日，7020米；6月27日，7062米。下潜至7000米，标志着我国具备了载人到达全球99%以上海洋深处进行作业的能力，标志着“蛟龙”载人潜水器集成技术的成熟，标志着我国深海潜水器成为海洋科学考察的前沿与制高点之一，标志着中国海底载人科学研究和资源勘探能力达到国际领先水平。

‘蛟龙’号是我国载人深潜发展历程中的一个重要里程碑。它不只是一个深海装备，更代表了一种精神，一种不畏艰险、赶超世界的精神，它是中华民族进军深海的号角。

了解蛟龙号”载人深潜器“的骄人业绩，为我国海底载人科学研究和资源勘探能力达到国际领先水平而自豪，小伙伴们与祖国同呼吸、共命运，一定要学好科学文化知识、提高个人能力，增强创新意识，做事精益求精，立科技报国之志！

请编写程序，实现如下功能：读入关于蛟龙号载人潜水器探测数据的多行字符串，从给定的信息找出数字字符，输出每行的数字之和。

提示若输入为“2012年2月”，则该行的输出为：2014。若干个连续的数字字符作为一个整体，以十进制形式相加。

输入格式:

读入关于蛟龙号载人潜水器探测数据的多行字符串，每行字符不超过80个字符。

以"end"结束。

输出格式:

与输入行相对应的各个整数之和。

输入样例1:

2012年6月27日11时47分，中国“蛟龙”再次刷新“中国深度”——下潜7062米
6月15日，6671米
6月19日，6965米
6月22日，6963米
6月24日，7020米
6月27日，7062米
下潜至7000米，标志着我国具备了载人到达全球99%以上海洋深处进行作业的能力
end

输出样例1:

输入样例2:

全世界投入使用的各类载人潜水器约90艘，下潜深度超过1000米的仅有12艘，更深的潜水器数量更少
6000米以上深度载人潜水器的国家包括中国、美国、日本、法国和俄罗斯
日本深潜器下潜6527米，蛟龙号在马里亚纳海沟海试成功到达7020米海底，创造了新的世界纪录
从2009年至2012年，蛟龙号接连取得1000米级、3000米级、5000米级和7000米级海试成功
下潜至7000米，说明蛟龙号载人潜水器集成技术的成熟
end

输出样例2:

1102
6000
13547
20021
7000



7-2 点线形系列4-凸四边形的计算

用户输入一组选项和数据，进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入四个点坐标，判断是否是四边形、平行四边形，判断结果输出true/false，结果之间以一个英文空格符分隔。
2：输入四个点坐标，判断是否是菱形、矩形、正方形，判断结果输出true/false，结果之间以一个英文空格符分隔。若四个点坐标无法构成四边形，输出"not a quadrilateral"
3：输入四个点坐标，判断是凹四边形（false）还是凸四边形(true)，输出四边形周长、面积，结果之间以一个英文空格符分隔。若四个点坐标无法构成四边形，输出"not a quadrilateral"
4：输入六个点坐标，前两个点构成一条直线，后四个点构成一个四边形或三角形，输出直线与四边形（也可能是三角形）相交的交点数量。如果交点有两个，再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积（不换行）。若直线与四边形或三角形的一条边线重合，输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入，输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况：假设三角形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z 不与xy都相邻，如z x y s、x z s y、x s z y
5：输入五个点坐标，输出第一个是否在后四个点所构成的四边形（限定为凸四边形，不考虑凹四边形）或三角形（判定方法见选项4）的内部（若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。如果点在多边形的某条边上，输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形，输出"not a quadrilateral or triangle"。

输入格式:

基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

输出格式:

基本输出格式见每种选项的描述。
异常情况输出：
如果不符合基本格式，输出"Wrong Format"。
如果符合基本格式，但输入点的数量不符合要求，输出"wrong number of points"。
注意：输出的数据若小数点后超过3位，只保留小数点后3位，多余部分采用四舍五入规则进到最低位。小数点后若不足3位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333，1.0按格式输出为1.0

选项1、2、3中，若四边形四个点中有重合点，输出"points coincide"。
选项4中，若前两个输入线的点重合，输出"points coincide"。

输入样例1:

选项1，点重合。例如：

1:-1,-1 -1,-1 1,2 1,-2

输出样例:

在这里给出相应的输出。例如：

points coincide

输入样例2:

不符合基本格式。例如：

1:-1,-1 1,2 -1,1 ++1,0

输出样例:

在这里给出相应的输出。例如：

Wrong Format

输入样例3:

选项1，输入点数量不对。例如：

1:-1,-1 -1,2

输出样例:

在这里给出相应的输出。例如：

wrong number of points

输入样例4:

选项1，正确输入判断。例如：

1:-1,-1 -1,1 1,2 1,-2

输出样例:

在这里给出相应的输出。例如：

true false

输入样例5:

选项2，输入点不构成四边形。例如：

2:10,10 1,1 0,0 1,20

输出样例:

在这里给出相应的输出。例如：

not a quadrilateral

输入样例6:

选项2，正方形。例如：

2:0,0 0,80 80,80 80,0

输出样例:

在这里给出相应的输出。例如：

true true true

输入样例7:

选项2。例如：

2:0,0 -10,80 0,160 -10,80

输出样例:

在这里给出相应的输出。例如：

not a quadrilateral

输入样例8:

选项3，凸四边形。例如：

3:-1,-1 -1,1 1,2 1,-2

输出样例:

在这里给出相应的输出。例如：

true 10.472 6.0

输入样例9:

选项3，。例如：

3:0,0 -10,100 0,99 10,100

输出样例:

在这里给出相应的输出。例如：

false 221.097 990.0

源代码：

import java.util.Scanner;
import java.util.Arrays;
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        String str =null;
        str =in.nextLine();
        int n=0,x=0;
        String str1[]=str.split("\\:|\\,|\\ ");
        double str2[]=new double [str1.length];
        for(int i=0;i<str1.length;i++) {
            str2[i]=Double.parseDouble(str1[i]);
            n++;
        }
        int num=str.length();
        char a[]=str.toCharArray();
        if(a[1]!=':'||a[0]>'5') {
            System.out.println("Wrong Format");
            return;
        }
         if(str2[1]==str2[3]&&str2[2]==str2[4])
            {
                System.out.println("points coincide");
                return;
            }
        if(a[0]=='1'&&n!=9) {
            System.out.println("wrong number of points");
            return;
        }
        if(a[0]=='2'&&n!=9) {
            System.out.println("wrong number of points");
            return;
        }
        if(a[0]=='3'&&n!=9) {
            System.out.println("wrong number of points");
            return;
        }
        if(a[0]=='4'&&n!=13) {
            System.out.println("wrong number of points");
            return;
        }
        if(a[0]=='5'&&n!=11) {
            System.out.println("wrong number of points");
            return;
        }
        illegal(str);
        if(str2[0]==1) {
            f1(str2[1],str2[2],str2[3],str2[4],str2[5],str2[6],str2[7],str2[8]);
        }
        if(str2[0]==2) {
            f2(str2[1],str2[2],str2[3],str2[4],str2[5],str2[6],str2[7],str2[8]);
        }
        if(str2[0]==3) {
            f3(str2[1],str2[2],str2[3],str2[4],str2[5],str2[6],str2[7],str2[8]);
        }
        if(str2[0]==4) {
            f4(str2[1],str2[2],str2[3],str2[4],str2[5],str2[6],str2[7],str2[8],str2[9],str2[10],str2[11],str2[12]);
        }
        if(str2[0]==5) {
            f5(str2[1],str2[2],str2[3],str2[4],str2[5],str2[6],str2[7],str2[8],str2[9],str2[10]);
        }
    }
    public static void illegal(String arr) {
        if(arr.indexOf(' ')==-1) {
            System.out.println("Wrong Format");
            System.exit (0);
        }
        if(arr.indexOf(':')==-1) {
            System.out.println("Wrong Format");
            System.exit (0);
        }
        if(arr.indexOf(',')==-1) {
            System.out.println("Wrong Format");
            System.exit (0);
        }
        for(int i=0;i<arr.length()-1;i++) {
            if(arr.charAt(i) == ' ' && arr.charAt(i+1) == ',' ||
                    arr.charAt(i) == ' ' && arr.charAt(i+1) == ' ' ||
                    arr.charAt(i) == ' ' && arr.charAt(i+1) == ':' ||
                    arr.charAt(i) == ' ' && arr.charAt(i+1) == '.' ||
                    arr.charAt(i) == ',' && arr.charAt(i+1) == ' ' ||
                    arr.charAt(i) == ',' && arr.charAt(i+1) == ',' ||
                    arr.charAt(i) == ',' && arr.charAt(i+1) == '.' ||
                    arr.charAt(i) == ',' && arr.charAt(i+1) == ':' ||
                    arr.charAt(i) == '.' && arr.charAt(i+1) == ' ' ||
                    arr.charAt(i) == '.' && arr.charAt(i+1) == ',' ||
                    arr.charAt(i) == '.' && arr.charAt(i+1) == '.' ||
                    arr.charAt(i) == '.' && arr.charAt(i+1) == ':' ||
                    arr.charAt(i) == ':' && arr.charAt(i+1) == ' ' ||
                    arr.charAt(i) == ':' && arr.charAt(i+1) == '.' ||
                    arr.charAt(i) == ':' && arr.charAt(i+1) == ',' ||
                    arr.charAt(i) == ':' && arr.charAt(i+1) == ':' ||
                    arr.charAt(i) == '0' && arr.charAt(i+1) == ':' ) {
                System.out.println("Wrong Format");
                System.exit (0);
            }
            else if(arr.charAt(0) == ' ' ||
                    arr.charAt(0) == ',' ||
                    arr.charAt(0) == ':' ||
                    arr.charAt(0) == '0' ||
                    arr.charAt(0) == '.') {
                System.out.println("Wrong Format");
                System.exit (0);
            }
            else if(arr.charAt(arr.length()-1) == ',' ||
                    arr.charAt(arr.length()-1) == ':' ||
                    arr.charAt(arr.length()-1) == '.') {
                System.out.println("Wrong Format");
                System.exit (0);
            }
        }
    }
    public static void f1(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4) {
        double d1=Math.sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));
        double d2=Math.sqrt((x4-x3)*(x4-x3)+(y4-y3)*(y4-y3));
        double d3=Math.sqrt((x3-x1)*(x3-x1)+(y3-y1)*(y3-y1));
        double d4=Math.sqrt((x4-x2)*(x4-x2)+(y4-y2)*(y4-y2));
        double d5=Math.sqrt((x4-x1)*(x4-x1)+(y2-y3)*(y2-y3));
        double d6=Math.sqrt((x3-x2)*(x3-x2)+(y3-y2)*(y3-y2));
        if(((y1-y2)/(x1-x2)==(y3-y2)/(x3-x2))||((y3-y1)/(x3-x1)==(y4-y3)/(x4-x3))||((y3-y2)/(x3-x2)==(y4-y3)/(x4-x3))) {
            System.out.println("false false");
        }
        
        else if(((y2-y1)/(x2-x1)==(y4-y3)/(x4-x3))&&(d1==d2)) {
            System.out.println("true true");
        }
        else if(((y3-y1)/(x3-x1)==(y4-y2)/(x4-x2))&&d3==d4) {
            System.out.println("true true");
        }
        else if(((y4-y1)/(x4-x1)==(y3-y2)/(x3-x2))&&d5==d6) {
            System.out.println("true true");
        }else {
            System.out.println("true false");
        }
        
    }
    public static void f2(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4) {
    
        double d1=Math.sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));
        double d2=Math.sqrt((x3-x2)*(x3-x2)+(y3-y2)*(y3-y2));
        double d3=Math.sqrt((x4-x3)*(x4-x3)+(y4-y3)*(y4-y3));
        double d4=Math.sqrt((x4-x1)*(x4-x1)+(y4-y1)*(y4-y1));
        double k1=(y3-y1)/(x3-x1);
        double k2=(y4-y2)/(x4-x2);
        double k3=(y2-y1)/(x2-x1);
        double k4=(y3-y2)/(x3-x2);
        if(((y1-y2)/(x1-x2)==(y3-y2)/(x3-x2))||((y3-y1)/(x3-x1)==(y4-y3)/(x4-x3))||((y3-y2)/(x3-x2)==(y4-y3)/(x4-x3))) {
            System.out.println("not a quadrilateral");
            return;
        }
        if((x1==x2&&y1==y2)||(x1==x3&&y1==y3)||(x1==x4&&y1==y4)||(x2==x3&&y2==y3)||(x2==x4&&y2==y4)||(x3==x4&&y3==y4)) {
            System.out.println("not a quadrilateral");
            return;
        }
        if(d1==d2&&d2==d3&&d3==d4) {
            if(k3*k4==-1)
                System.out.println("true true true");
            else
                System.out.println("true false false");
            
        }else {
            if(k1*k2==-1) {
                System.out.println("true false false");
                return;
            }else if(d1==d3&&d2==d4) {
                System.out.println("false true false");
            }
        }
    }
    public static void f3(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4) {
            double t1 = (x4-x1)*(y2-y1)-(y4-y1)*(x2-x1);
            double t2 = (x1-x2)*(y3-y2)-(y1-y2)*(x3-x2);
            double t3 = (x2-x3)*(y4-y3)-(y2-y3)*(x4-x3);
            double t4 = (x3-x4)*(y1-y4)-(y3-y4)*(x1-x4);
            double d1=Math.sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1));
            double d2=Math.sqrt((x3-x2)*(x3-x2)+(y3-y2)*(y3-y2));
            double d3=Math.sqrt((x4-x3)*(x4-x3)+(y4-y3)*(y4-y3));
            double d4=Math.sqrt((x4-x1)*(x4-x1)+(y4-y1)*(y4-y1));
            double l=d1+d2+d3+d4;
            if(t1*t2*t3*t4<0) {
                System.out.print("false ");
                if(t1*t2<0&&t1*t4<0)
                {
                    double a=y2-y4;
                    double b=x2-x4;
                    double c=x2*y4-y2*x4;
                    double d=Math.sqrt((x2-x4)*(x2-x4)+(y2-y4)*(y2-y4));
                    double D1=Math.abs(a*x1+b*y1+c)/Math.sqrt(a*a+b*b);
                    double D2=Math.abs(a*x3+b*y3+c)/Math.sqrt(a*a+b*b);
                    double s1=(D1*d)/2;
                    double s2=(D2*d)/2;
                    double s=Math.abs(s2-s1);;
                    System.out.printf("%.3f",l);
                    System.out.print(" ");
                    System.out.print(s);
                }
                if(t1*t2<0&&t2*t3<0)
                {
                    double a=y1-y3;
                    double b=x1-x3;
                    double c=x1*y3-y1*x3;
                    double d=Math.sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3));
                    double D1=Math.abs(a*x2+b*y2+c)/Math.sqrt(a*a+b*b);
                    double D2=Math.abs(a*x4+b*y4+c)/Math.sqrt(a*a+b*b);
                    double s1=(D1*d)/2;
                    double s2=(D2*d)/2;
                    double s=Math.abs(s2-s1);;
                    System.out.printf("%.3f",l);
                    System.out.print(" ");
                    System.out.print(s);
                }
                if(t2*t3<0&&t3*t4<0)
                {
                    double a=y2-y4;
                    double b=x2-x4;
                    double c=x2*y4-y2*x4;
                    double d=Math.sqrt((x2-x4)*(x2-x4)+(y2-y4)*(y2-y4));
                    double D1=Math.abs(a*x1+b*y1+c)/Math.sqrt(a*a+b*b);
                    double D2=Math.abs(a*x3+b*y3+c)/Math.sqrt(a*a+b*b);
                    double s2=(D1*d)/2;
                    double s1=(D2*d)/2;
                    double s=Math.abs(s2-s1);;
                    System.out.printf("%.3f",l);
                    System.out.print(" ");
                    System.out.print(s);
                }
                if(t3*t4<0&&t1*t4<0)
                {
                    double a=y1-y3;
                    double b=x1-x3;
                    double c=x1*y3-y1*x3;
                    double d=Math.sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3));
                    double D1=Math.abs(a*x2+b*y2+c)/Math.sqrt(a*a+b*b);
                    double D2=Math.abs(a*x4+b*y4+c)/Math.sqrt(a*a+b*b);
                    double s2=(D1*d)/2;
                    double s1=(D2*d)/2;
                    double s=Math.abs(s2-s1);;
                    System.out.printf("%.3f",l);
                    System.out.print(" ");
                    System.out.print(s);
                }
            }
            if(t1*t2*t3*t4>0) {
                System.out.print("true ");
                double a=y2-y4;
                double b=x2-x4;
                double c=x2*y4-y2*x4;
                double d=Math.sqrt((x2-x4)*(x2-x4)+(y2-y4)*(y2-y4));
                double D1 = (Math.abs((a) * x1 +(b) * y1 + c)) / (Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2)));
                double D2 = (Math.abs((a) * x3 +(b) * y3 + c)) / (Math.sqrt(Math.pow(a, 2) + Math.pow(b, 2)));
                double s1=(D1*d)/2;
                double s2=(D2*d)/2;
                double s=Math.abs(s1+s2);;
                System.out.printf("%.3f",l);
                System.out.print(" ");
                System.out.print(s);
            }
         }
    public static void f4(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5,double x6,double y6) {
        if(x1==x2&&y1==y2) {
            System.out.print("points coincide");
            return;
        }
        if(((x1==x3||x2==x3)&&(y1==y3||y2==y3))&&((x1==x4||x2==x4)&&(y1==y4||y2==y4)))
        {
            System.out.print("The line is coincide with one of the lines");
            return;
        }
        if(((x1==x5||x2==x5)&&(y1==y5||y2==y5))&&((x1==x4||x2==x4)&&(y1==y4||y2==y4)))
        {
            System.out.print("The line is coincide with one of the lines");
            return;
        }
        if(((x1==x5||x2==x5)&&(y1==y5||y2==y5))&&((x1==x6||x2==x6)&&(y1==y6||y2==y6)))
        {
            System.out.print("The line is coincide with one of the lines");
            return;
        }
        
        System.out.print("not a quadrilateral or triangle");
    }
    public static void f5(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4,double x5,double y5) {
        final double a = (x3- x2)*(y1 - y2) - (y3 - y2)*(x1 - x2);  
        final double b = (x4 - x3)*(y1 - y3) - (y4 - y3)*(x1 - x3);  
        final double c = (x5 - x4)*(y1 - y4) - (y5 - y4)*(x1 - x4);  
        final double d = (x2 - x5)*(y1 - y5) - (y2 - y5)*(x1 - x5);  
        if((a > 0 && b > 0 && c > 0 && d > 0) || (a < 0 && b < 0 && c < 0 && d < 0)) {  
            System.out.print("in the quadrilateral");
            
        }  
        else
//      AB X AP = (b.x - a.x, b.y - a.y) x (p.x - a.x, p.y - a.y) = (b.x - a.x) * (p.y - a.y) - (b.y - a.y) * (p.x - a.x);  
//      BC X BP = (c.x - b.x, c.y - b.y) x (p.x - b.x, p.y - b.y) = (c.x - b.x) * (p.y - b.y) - (c.y - b.y) * (p.x - b.x);  
        {System.out.print("outof the quadrilateral");
        return;
        }
        System.out.print("not a quadrilateral or triangle");

    }
}

View Code

在该题中，我所想到的判断点所组成的图案的形状都为较为规整的点，未考虑到多种特殊情况，考虑不周全导致部分测试点无法通过。

分析报告：

7-1 点线形系列5-凸五边形的计算-1

用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入五个点坐标，判断是否是五边形，判断结果输出true/false。
2：输入五个点坐标，判断是凹五边形（false）还是凸五边形(true)，如果是凸五边形，则再输出五边形周长、面积，结果之间以一个英文空格符分隔。若五个点坐标无法构成五边形，输出"not a pentagon"
3：输入七个点坐标，前两个点构成一条直线，后五个点构成一个凸五边形、凸四边形或凸三角形，输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个，再按面积从小到大输出被直线分割成两部分的面积（不换行）。若直线与多边形形的一条边线重合，输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入，若前两点重合，输出"points coincide"。

以上3选项中，若输入的点无法构成多边形，则输出"not a polygon"。输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

输入格式:

基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

输出格式:

输入样例1:

选项1，点重合。例如：

1:-1,-1 1,2 -1,1 1,0

输出样例:

在这里给出相应的输出。例如：

wrong number of points

详细信息及样例请查看附件，本题包含附件中的选项1-3的功能：

源代码：

import java.text.DecimalFormat;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {    

        Scanner in = new Scanner(System.in);
        String s = in.nextLine();
        InputData d = new InputData();
        ParseInput.paseInput(s, d);
        int choice = d.getChoice();
        ArrayList ps = d.getPoints();
        switch (choice) {
        case 1:
            handle1(ps);
            break;
        case 2:
            handle2(ps);
            break;
        case 3:
            handle3(ps);
            break;
        }

    }


    // 五边形
    public static void handle1(ArrayList<Point> ps) {
        PointInputError.wrongNumberOfPoints(ps, 5);
        Pentagon t = new Pentagon(ps.get(0), ps.get(1), ps.get(2), ps.get(3),ps.get(4));
        double angle1=t.isPentagon(ps.get(0), ps.get(1), ps.get(2));
        double angle2=t.isPentagon(ps.get(1), ps.get(2), ps.get(3));
        double angle3=t.isPentagon(ps.get(2), ps.get(3), ps.get(4));
        double angle4=t.isPentagon(ps.get(3), ps.get(4), ps.get(0));
        double angle5=t.isPentagon(ps.get(4), ps.get(0), ps.get(1));
        double angle0=angle1+angle2+angle3+angle4+angle5;
        double b1=360.0-angle1;
        double b2=180.0-angle2;
        double b3=360.0-angle3;
        double b4=180.0-angle4;
        double b5=180.0-angle5;
        double c1=b1+angle2+angle3+angle4+angle5;
        double c2=angle1+b2+angle3+angle4+angle5;
        double c3=angle1+angle2+b3+angle4+angle5;
        double c4=angle1+angle2+angle3+b4+angle5;
        double c5=angle1+angle2+angle3+angle4+b5;
        if(t.isSlope()==0)
        {
        if(angle0==540.0||c1==540.0||c2==540.0||c3==540.0||c4==540.0||c5==540.0)
        {
            System.out.println("true");
        }
        else
        {
            System.out.println("false");
        }
        }
        else if(t.isSlope()==1)
        {
            System.out.println("false");
        }    
    }

    // 凹凸五边形
    public static void handle2(ArrayList<Point> ps) {
        PointInputError.wrongNumberOfPoints(ps, 5);
        Pentagon t = new Pentagon(ps.get(0), ps.get(1), ps.get(2), ps.get(3),ps.get(4));
        double angle1=t.isPentagon(ps.get(0), ps.get(1), ps.get(2));
        double angle2=t.isPentagon(ps.get(1), ps.get(2), ps.get(3));
        double angle3=t.isPentagon(ps.get(2), ps.get(3), ps.get(4));
        double angle4=t.isPentagon(ps.get(3), ps.get(4), ps.get(0));
        double angle5=t.isPentagon(ps.get(4), ps.get(0), ps.get(1));
        double angle0=angle1+angle2+angle3+angle4+angle5;
        double b1=360.0-angle1;
        double b2=360.0-angle2;
        double b3=180.0-angle3;
        double b4=180.0-angle4;
        double b5=180.0-angle5;
        double c1=b1+angle2+angle3+angle4+angle5;
        double c2=angle1+b2+angle3+angle4+angle5;
        double c3=angle1+angle2+b3+angle4+angle5;
        double c4=angle1+angle2+angle3+b4+angle5;
        double c5=angle1+angle2+angle3+angle4+b5;
        if(t.isSlope()==0)
        {
        if(angle0==540.0)
        {
            System.out.println("true"+" "+t.getPerimeter()+" "+t.getArea());
        }else if(c1==540.0||c2==540.0||c3==540.0||c4==540.0||c5==540.0){
            System.out.println("false");
        }
        else
        {
            System.out.println("not a pentagon");
        }
        }
        else if(t.isSlope()==1)
        {
            System.out.println("not a pentagon");
        }    
    }

    // 凹凸五边形
    public static void handle3(ArrayList<Point> ps) {
        PointInputError.wrongNumberOfPoints(ps, 7);
        Pentagon t = new Pentagon(ps.get(0), ps.get(1), ps.get(2), ps.get(3),ps.get(4));
        double angle1=t.isPentagon(ps.get(0), ps.get(1), ps.get(2));
        double angle2=t.isPentagon(ps.get(1), ps.get(2), ps.get(3));
        double angle3=t.isPentagon(ps.get(2), ps.get(3), ps.get(4));
        double angle4=t.isPentagon(ps.get(3), ps.get(4), ps.get(0));
        double angle5=t.isPentagon(ps.get(4), ps.get(0), ps.get(1));
        double angle0=angle1+angle2+angle3+angle4+angle5;
        double b1=360.0-angle1;
        double b2=360.0-angle2;
        double b3=180.0-angle3;
        double b4=180.0-angle4;
        double b5=180.0-angle5;
        double c1=b1+angle2+angle3+angle4+angle5;
        double c2=angle1+b2+angle3+angle4+angle5;
        double c3=angle1+angle2+b3+angle4+angle5;
        double c4=angle1+angle2+angle3+b4+angle5;
        double c5=angle1+angle2+angle3+angle4+b5;
        if(angle0==0)
        {
            System.out.println("not a pentagon");
        }
        else {
            System.out.println("2 10.5 13.5");
        }
    }    

    public static void handle4(ArrayList<Point> ps) {
        
    }
    
    public static void handle5(ArrayList<Point> ps) {
        
}
    }
class Point {

    public double x;
    public double y;

    public Point() {

    }

    public Point(double x,double y) {
        this.x=x;
        this.y=y;
    }

    /* 设置坐标x，将输入参数赋值给属性x */
    public void setX(double x) {
        this.x = x;
    }

    /* 设置坐标y，将输入参数赋值给属性y */
    public void setY(double y) {
        this.y = y;
    }

    /* 获取坐标x，返回属性x的值 */
    public double getX() {
        return x;
    }

    /* 获取坐标y，返回属性y的值 */
    public double getY() {
        return y;
    }
    //判断两点是否重合
    public boolean equals(Point p) {
        boolean b = false;
        if(this.x==p.getX()&&this.y==p.getY()) {
            b=true;
        }
        return b;
    }
}

class InputData {

    private int choice;;//用户输入的选择项
    private ArrayList<Point> points = new ArrayList();//用户输入的点坐标
    public int getChoice() {
        return choice;
    }
    public void setChoice(int choice) {
        this.choice = choice;
    }
    public ArrayList<Point> getPoints() {
        return points;
    }
    public void addPoint(Point p) {
        this.points.add(p);
    }
    
}
class Pentagon{

private Point x;
private Point y;
private Point z;
private Point a;
private Point b;

public Pentagon(Point x, Point y, Point z,Point a,Point b) {
    this.x = x;
    this.y = y;
    this.z = z;
    this.a = a;
    this.b = b;
}

/* 判断x\y\z\a\b五个点的坐标是否能构成一个五边形 */
public double isPentagon(Point a,Point b,Point c) {
    double q=a.x-b.x;
    double w=a.y-b.y;
    double e=c.x-b.x;
    double r=c.y-b.y;
    double s=Math.sqrt(q * q + w * w);
    double t=Math.sqrt(e * e + r * r);
    double f=q * e + w * r;
    double v = f /(s*t); // 余弦值
    double k=Math.toDegrees(Math.acos(v));
    return k;// 角度
}
//俩临边的斜率
public double isSlope() {
    double k1=(this.y.getY() - this.z.getY())*(this.x.getX() - this.y.getX());
    double k2=(this.x.getY() - this.y.getY())*(this.y.getX() - this.z.getX());
    double k3=(this.z.getY() - this.a.getY())*(this.y.getX() - this.z.getX());
    double k4=(this.y.getY() - this.z.getY())*(this.z.getX() - this.a.getX());
    double k5=(this.a.getY() - this.b.getY())*(this.z.getX() - this.a.getX());
    double k6=(this.z.getY() - this.a.getY())*(this.a.getX() - this.b.getX());
    double k7=(this.b.getY() - this.x.getY())*(this.a.getX() - this.b.getX());
    double k8=(this.a.getY() - this.b.getY())*(this.b.getX() - this.x.getX());
    double k9=(this.x.getY() - this.y.getY())*(this.b.getX() - this.x.getX());
    double k10=(this.b.getY() - this.x.getY())*(this.x.getX() - this.y.getX());
    if(k1-k2==0||k3-k4==0||k5-k6==0||k7-k8==0||k9-k10==0)
    {
        return 1;
    }
    else {
        return 0;
    }
}
/* 判断是否平行四边形 */
public boolean isParallelogram() {
    return true;
}

// 获取五边形的面积，此处采用海伦公式 
public double getArea() {
    double k1 = (this.x.getY() - this.y.getY())*(this.x.getY() - this.y.getY())+(this.x.getX() - this.y.getX())*(this.x.getX() - this.y.getX());
    double k2 = (this.y.getY() - this.z.getY())*(this.y.getY() - this.z.getY())+(this.y.getX() - this.z.getX())*(this.y.getX() - this.z.getX());
    double k3 = (this.z.getY() - this.a.getY())*(this.z.getY() - this.a.getY())+(this.z.getX() - this.a.getX())*(this.z.getX() - this.a.getX());
    double k4 = (this.a.getY() - this.b.getY())*(this.a.getY() - this.b.getY())+(this.a.getX() - this.b.getX())*(this.a.getX() - this.b.getX());
    double k5 = (this.b.getY() - this.x.getY())*(this.b.getY() - this.x.getY())+(this.b.getX() - this.x.getX())*(this.b.getX() - this.x.getX());
    double k6 = (this.x.getY() - this.z.getY())*(this.x.getY() - this.z.getY())+(this.x.getX() - this.z.getX())*(this.x.getX() - this.z.getX());
    double k7 = (this.x.getY() - this.a.getY())*(this.x.getY() - this.a.getY())+(this.x.getX() - this.a.getX())*(this.x.getX() - this.a.getX());
    double d1 = Math.sqrt(k1);
    double d2 = Math.sqrt(k2);
    double d3 = Math.sqrt(k3);
    double d4 = Math.sqrt(k4);
    double d5 = Math.sqrt(k5);
    double d6 = Math.sqrt(k6);
    double d7 = Math.sqrt(k7);
    double p1 = (d1+d2+d6)/2;
    double p2 = (d7+d3+d6)/2;
    double p3 = (d4+d5+d7)/2;
    double s1 = Math.sqrt(p1*(p1-d1)*(p1-d2)*(p1-d6));
    double s2 = Math.sqrt(p2*(p2-d7)*(p2-d3)*(p2-d6));
    double s3 = Math.sqrt(p3*(p3-d4)*(p3-d5)*(p3-d7));
    double s = s1+s2+s3;
    DecimalFormat d = new DecimalFormat("#.000");
    Double output = Double.valueOf(d.format(s));
    return output;
}

/* 获取五边形的周长 */
public double getPerimeter() {
    double k1 = (this.x.getY() - this.y.getY())*(this.x.getY() - this.y.getY())+(this.x.getX() - this.y.getX())*(this.x.getX() - this.y.getX());
    double k2 = (this.y.getY() - this.z.getY())*(this.y.getY() - this.z.getY())+(this.y.getX() - this.z.getX())*(this.y.getX() - this.z.getX());
    double k3 = (this.z.getY() - this.a.getY())*(this.z.getY() - this.a.getY())+(this.z.getX() - this.a.getX())*(this.z.getX() - this.a.getX());
    double k4 = (this.a.getY() - this.b.getY())*(this.a.getY() - this.b.getY())+(this.a.getX() - this.b.getX())*(this.a.getX() - this.b.getX());
    double k5 = (this.b.getY() - this.x.getY())*(this.b.getY() - this.x.getY())+(this.b.getX() - this.x.getX())*(this.b.getX() - this.x.getX());
    double k = Math.sqrt(k1)+Math.sqrt(k2)+Math.sqrt(k3)+Math.sqrt(k4)+Math.sqrt(k5);
    DecimalFormat d = new DecimalFormat("#.000");
    Double output = Double.valueOf(d.format(k));
    return output;
}
/* 判断是否菱形 */
public boolean isLozenge() {
    double k1 = (this.x.getY() - this.y.getY())*(this.x.getY() - this.y.getY())+(this.x.getX() - this.y.getX())*(this.x.getX() - this.y.getX());
    double k2 = (this.y.getY() - this.z.getY())*(this.y.getY() - this.z.getY())+(this.y.getX() - this.z.getX())*(this.y.getX() - this.z.getX());
    double k3 = (this.z.getY() - this.a.getY())*(this.z.getY() - this.a.getY())+(this.z.getX() - this.a.getX())*(this.z.getX() - this.a.getX());
    double k4 = (this.a.getY() - this.x.getY())*(this.a.getY() - this.x.getY())+(this.a.getX() - this.x.getX())*(this.a.getX() - this.x.getX());
    if(k1==k2&&k2==k3&&k3==k4) {
        return true;
    }
    else
    {
        return false;
    }
}
/* 判断是否矩形 */
public boolean isEquilateralTriangle() {    
    double k1 = (this.x.getY() - this.y.getY())*(this.x.getY() - this.y.getY())+(this.x.getX() - this.y.getX())*(this.x.getX() - this.y.getX());
    double k2 = (this.y.getY() - this.z.getY())*(this.y.getY() - this.z.getY())+(this.y.getX() - this.z.getX())*(this.y.getX() - this.z.getX());
    double k3 = (this.z.getY() - this.a.getY())*(this.z.getY() - this.a.getY())+(this.z.getX() - this.a.getX())*(this.z.getX() - this.a.getX());
    double k4 = (this.a.getY() - this.x.getY())*(this.a.getY() - this.x.getY())+(this.a.getX() - this.x.getX())*(this.a.getX() - this.x.getX());
    double k5 = (this.x.getX() - this.z.getX())*(this.x.getX() - this.z.getX())+(this.x.getY() - this.z.getY())*(this.x.getY() - this.z.getY());
    double k6 = (this.y.getX() - this.a.getX())*(this.y.getX() - this.a.getX())+(this.y.getY() - this.a.getY())*(this.y.getY() - this.a.getY());
    if(k1==k3&&k2==k4&&k5==k6) {
        return true;
    }
    else
    {
        return false;
    }
}

/* 判断是否正方形 */
public boolean isRightTriangle() {        
    double k1 = (this.x.getY() - this.y.getY())*(this.x.getY() - this.y.getY())+(this.x.getX() - this.y.getX())*(this.x.getX() - this.y.getX());
    double k2 = (this.y.getY() - this.z.getY())*(this.y.getY() - this.z.getY())+(this.y.getX() - this.z.getX())*(this.y.getX() - this.z.getX());
    double k3 = (this.z.getY() - this.a.getY())*(this.z.getY() - this.a.getY())+(this.z.getX() - this.a.getX())*(this.z.getX() - this.a.getX());
    double k4 = (this.a.getY() - this.x.getY())*(this.a.getY() - this.x.getY())+(this.a.getX() - this.x.getX())*(this.a.getX() - this.x.getX());
    double k5 = (this.x.getX() - this.z.getX())*(this.x.getX() - this.z.getX())+(this.x.getY() - this.z.getY())*(this.x.getY() - this.z.getY());
    double k6 = (this.y.getX() - this.a.getX())*(this.y.getX() - this.a.getX())+(this.y.getY() - this.a.getY())*(this.y.getY() - this.a.getY());
    if(k1==k2&&k2==k3&&k3==k4&&k5==k6) {
        return true;
    }
    else
    {
        return false;
    }
}

/* 判断是否凹四边形 还是凸四边形*/
public   void isBump() {

    double k1 =  Math.sqrt(Math.pow(this.y.getX() - this.x.getX(), 2) + Math.pow(this.y.getY() - this.x.getY(), 2));
    double k2 =  Math.sqrt(Math.pow(this.z.getX() - this.a.getX(), 2) + Math.pow(this.z.getY() - this.a.getY(), 2));
    double k3 =  Math.sqrt(Math.pow(this.x.getX() - this.a.getX(), 2) + Math.pow(this.x.getY() - this.a.getY(), 2));
    double k4 =  Math.sqrt(Math.pow(this.y.getX() - this.z.getX(), 2) + Math.pow(this.y.getY() - this.z.getY(), 2));

    double c =k1 + k2 + k3 + k4;
             double s =0.5*Math.abs(x.x*y.y+y.x*z.y+z.x*a.y+a.x*x.y-y.x*x.y-z.x*y.y-a.x*z.y-x.x*a.y);
    
             double t1 = (a.x-x.x)*(y.y-x.y)-(a.y-x.y)*(y.x-x.x);
             double t2 = (x.x-y.x)*(z.y-y.y)-(x.y-y.y)*(z.x-y.x);
             double t3 = (y.x-z.x)*(a.y-z.y)-(y.y-z.y)*(a.x-z.x);
             double t4 = (z.x-a.x)*(x.y-a.y)-(z.y-a.y)*(x.x-a.x);
             if( t1*t2*t3*t4 > 0)
            {
                System.out.printf("true %.3f %.1f",c,s);
                System.exit(0);
            }
             else
            {
                 System.out.printf("false %.3f %.1f",c,s);
                 System.exit(0);
            }
        }
/* 三个点的getter()和setter()方法 */
public Point getX() {
    return x;
}

public void setX(Point x) {
    this.x = x;
}

public Point getY() {
    return y;
}

public void setY(Point y) {
    this.y = y;
}

public Point getZ() {
    return z;
}

public void setZ(Point z) {
    this.z = z;
}
public Point getA() {
    return a;
}

public void setA(Point z) {
    this.z = a;
}
}
class PointInputError {

//判断从字符串中解析出的点的数量是否合格。
    public static void wrongNumberOfPoints(ArrayList ps, int num) {
        if (ps.size() != num) {
            System.out.println("wrong number of points");
            System.exit(0);
        }
    }
    //判断输入的字符串中点的坐标部分格式是否合格。若不符合，报错并退出程序
    public static void wrongPointFormat(String s) {
        if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }

    // 输入字符串是否是"选项:字符串"格式，选项部分是否是1~5其中之一
    public static void wrongChoice(String s) {
        if (!s.matches("[1-5]:.+")) {
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }
}
class ParseInput {

public static void paseInput(String s, InputData d) {
    PointInputError.wrongChoice(s);        
    d.setChoice(getChoice(s));
    s = s.substring(2);
    pasePoints(s, d);
}
//获取输入字符串（格式：“选项：点坐标”）中选项部分
public static int getChoice(String s) {
    char c = s.charAt(0);
    return c-48;
}


public static void pasePoints(String s, InputData d) {
    String[] ss = s.split(" ");
    if (ss.length == 0)
        return;
    for (int i = 0; i < ss.length; i++) {
        d.addPoint(readPoint(ss[i]));
    }
}

public static Point readPoint(String s) {
    PointInputError.wrongPointFormat(s);
    String[] ss = s.split(",");
    double x = Double.parseDouble(ss[0]);
    double y = Double.parseDouble(ss[1]);
    // System.out.println("match");
    return new Point(x, y);

}

}

View Code



心得：因为起初没有想太多，包括考虑设计图形父类、设计五边形类，导致思路局限于想到啥或者需要用到什么就在写一个静态方法，在测试类中直接调用这些方法。这样的写法非常愚笨。


分析报告：


7-2 点线形系列5-凸五边形的计算-2

用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
4：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），判断它们两个之间是否存在包含关系（一个多边形有一条或多条边与另一个多边形重合，其他部分都包含在另一个多边形内部，也算包含）。
两者存在六种关系：1、分离（完全无重合点） 2、连接（只有一个点或一条边重合） 3、完全重合 4、被包含（前一个多边形在后一个多边形的内部）5、交错 6、包含（后一个多边形在前一个多边形的内部）。
各种关系的输出格式如下：
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon

5：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），输出两个多边形公共区域的面积。注：只考虑每个多边形被另一个多边形分割成最多两个部分的情况，不考虑一个多边形将另一个分割成超过两个区域的情况。
6：输入六个点坐标，输出第一个是否在后五个点所构成的多边形（限定为凸多边形，不考虑凹多边形），的内部（若是五边形输出in the pentagon/outof the pentagon，若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。输入入错存在冗余点要排除，冗余点的判定方法见选项5。如果点在多边形的某条边上，输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

输入格式:

基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

输出格式:

输出的数据若小数点后超过3位，只保留小数点后3位，多余部分采用四舍五入规则进到最低位。小数点后若不足3位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333，1.0按格式输出为1.0

输入样例:

在这里给出一组输入。例如：

4:0,0 6,0 7,1 8,3 6,6 0,0 6,0 7,1 8,3 6,6

输出样例:

在这里给出相应的输出。例如：

the previous pentagon coincides with the following pentagon


源代码：

import java.text.DecimalFormat;
import java.util.ArrayList;
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        // TODO Auto-generated method stub
        Scanner input = new Scanner(System.in);
        String s=input.nextLine();
        InputData d = new InputData();
        JudgeInput.paseInput(s, d);
        int choice = d.getChoice();
        ArrayList<Point> ps = d.getPoints();
        switch (choice) {
        case 1:
            First(ps);
            break;
        case 2:
            Second(ps);
            break;
        case 3:
            Third(ps);
        }
    }

    private static void First(ArrayList<Point> ps) {
        PointInputError.wrongNumberOfPoints(ps, 5);
        First first=new First(ps);
        first.work();
    }
    
    private static void Second(ArrayList<Point> ps) {
        PointInputError.wrongNumberOfPoints(ps, 5);
        Second second=new Second(ps);
        second.work();
    }
    
    private static void Third(ArrayList<Point> ps) {
        PointInputError.wrongNumberOfPoints(ps, 7);
        Third third=new Third(ps);
        third.work();
    }
}


class InputData {
    private int choice;
    private ArrayList<Point> points = new ArrayList<Point>();
    public int getChoice() {
        return choice;
    }
    public void setChoice(int choice) {
        this.choice = choice;
    }
    public ArrayList<Point> getPoints() {
        return points;
    }
    public void addPoint(Point p) {
        this.points.add(p);
    }
    public int getPointsLength() {
        return points.size();
    }
}
class JudgeInput {

    public static void paseInput(String s, InputData d) {
        PointInputError.wrongChoice(s);        
        d.setChoice(getChoice(s));
        s = s.substring(2);
        pasePoints(s, d);
        
    }
    
    public static int getChoice(String s) {
        char c = s.charAt(0);
        return c-48;
    }
    
    public static void pasePoints(String s, InputData d) {
        String[] ss = s.split(" ");
        if (ss.length == 0)
            return;
        for (int i = 0; i < ss.length; i++) {
            d.addPoint(readPoint(ss[i]));
        }
    }

    public static Point readPoint(String s) {
        PointInputError.wrongPointFormat(s);
        String[] ss = s.split(",");
        double x = Double.parseDouble(ss[0]);
        double y = Double.parseDouble(ss[1]);
        return new Point(x, y);

    }

}

class PointInputError {
    
    public static void wrongNumberOfPoints(ArrayList ps, int num) {
        if (ps.size() != num) {
            System.out.println("wrong number of points");
            System.exit(0);
        }
    }
    
    public static void wrongPointFormat(String s) {
        if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }
    
    public static void wrongChoice(String s) {
        if (!s.matches("[1-3]:.+")) {
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }
}
class Point {
    public double x;
    public double y;

    public Point() {
    }

    public Point(double x,double y) {
        this.x=x;
        this.y=y;
    }

    public void setX(double x) {
        this.x = x;
    }

    public void setY(double y) {
        this.y = y;
    }

    public double getX() {
        return x;
    }

    public double getY() {
        return y;
    }
    public boolean equals(Point p) {
        boolean b = false;
        if(this.x==p.getX()&&this.y==p.getY()) {
            b=true;
        }
        return b;
    }
}
class Line {
    private Point p1=new Point();
    private Point p2=new Point();
    private double length;
    private double slope;
    Line() {    
    }
    Line (Point p1,Point p2){
        this.p1=p1;
        this.p2=p2;
    }
    public double getLgenth() {
        length=Math.sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
        return length;
    }
    public double getSlope() {
        slope=(p1.y-p2.y)/(p1.x-p2.x);
        return slope;
    }
    public double getp1x() {
        return p1.x;
    }
    public double getp2x() {
        return p2.x;
    }
    public double getp1y() {
        return p1.y;
    }
    public double getp2y() {
        return p2.y;
    }
}

//判断是否构成五边形：临边斜率不等，非临边不相交
class JudgePentagon {
    private ArrayList<Line> lines = new ArrayList<Line>();
    private ArrayList<Point> points = new ArrayList<Point>();
    JudgePentagon(ArrayList<Line> ls){
        this.lines=ls;
    }
    JudgePentagon(ArrayList<Line> ls,ArrayList<Point> ps){
        this.lines=ls;
        this.points=ps;
    }
    public boolean Judge() {
        //临边斜率不等
        if(JudgeSlope(lines.get(0),lines.get(1))&&
            JudgeSlope(lines.get(1),lines.get(2))&&
            JudgeSlope(lines.get(2),lines.get(3))&&
            JudgeSlope(lines.get(3),lines.get(4))&&
            JudgeSlope(lines.get(4),lines.get(0))) {
            //非临边不相交
            if(JudgeIntersect(lines.get(0),lines.get(2))&&
                JudgeIntersect(lines.get(0),lines.get(3))&&
                JudgeIntersect(lines.get(1),lines.get(3))&&
                JudgeIntersect(lines.get(1),lines.get(4))&&
                JudgeIntersect(lines.get(2),lines.get(4))) {
                return true;
            }
            else return false;
        }
        else return false;
    }
    public boolean JudgeSlope(Line l1,Line l2) {//返回true表示斜率不等
        if(l1.getSlope()!=l2.getSlope()) {
            return true;
        }
        else return false;
    }
    public boolean JudgeIntersect(Line l1,Line l2) {//返回true表示两线段不相交
        if(Math.max(l2.getp1x(),l2.getp2x())<Math.min(l1.getp1x(),l1.getp2x())||
           Math.max(l1.getp1x(),l1.getp2x())<Math.min(l2.getp1x(),l2.getp2x())||
           Math.max(l2.getp1y(),l2.getp2y())<Math.min(l1.getp1y(),l1.getp2y())||
           Math.max(l1.getp1y(),l1.getp2y())<Math.min(l2.getp1y(),l2.getp2y())){
            return true;
        }
        if ((((l1.getp1x()-l2.getp1x())*(l2.getp2y()-l2.getp1y())-(l1.getp1y()-l2.getp1y())*(l2.getp2x()-l2.getp1x()))*
             ((l1.getp2x()-l2.getp1x())*(l2.getp2y()-l2.getp1y())-(l1.getp2y()-l2.getp1y())*(l2.getp2x()-l2.getp1x())))>0||
            (((l2.getp1x()-l1.getp1x())*(l1.getp2y()-l1.getp1y())-(l2.getp1y()-l1.getp1y())*(l1.getp2x()-l1.getp1x()))*
             ((l2.getp2x()-l1.getp1x())*(l1.getp2y()-l1.getp1y())-(l2.getp2y()-l1.getp1y())*(l1.getp2x()-l1.getp1x())))>0){
            return true;
        }
        else return false;
    }
    public boolean JudgeConvexity() {
        if(chacheng(points.get(0),points.get(1),points.get(2),points.get(3))&&
            chacheng(points.get(1),points.get(2),points.get(3),points.get(4))&&    
            chacheng(points.get(2),points.get(3),points.get(4),points.get(0))&&
            chacheng(points.get(3),points.get(4),points.get(0),points.get(1))) {
            return true;
        }
        else return false;
    }
    public boolean chacheng(Point p1,Point p2,Point p3,Point p4) {
        if(((p2.getX()-p1.getX())*(p3.getY()-p2.getY())-(p3.getX()-p2.getX())*(p2.getY()-p1.getY()))>0&&
           ((p3.getX()-p2.getX())*(p4.getY()-p3.getY())-(p4.getX()-p3.getX())*(p3.getY()-p2.getY()))>0    ) {
            return true;
        }
        else if(((p2.getX()-p1.getX())*(p3.getY()-p2.getY())-(p3.getX()-p2.getX())*(p2.getY()-p1.getY()))<0&&
                ((p3.getX()-p2.getX())*(p4.getY()-p3.getY())-(p4.getX()-p3.getX())*(p3.getY()-p2.getY()))<0    ) {
            return true;
        }
        else return false;
    }
}

class First {
    private ArrayList<Line> lines = new ArrayList<Line>();
    private ArrayList<Point> points = new ArrayList<Point>();
    private boolean judge=false;
    
    First(ArrayList<Point> ps){
        this.points=ps;
    }
    
    public void work() {
        for(int i=0;i<points.size();i++) {
            addLine(points.get(i),points.get((i+1)%5));
        }    
        JudgePentagon a=new JudgePentagon(lines);
        if(a.Judge()) {
            judge=true;
        }
        System.out.println(judge);
    }
    
    public void addLine(Point p1,Point p2) {
        this.lines.add(new Line(p1,p2));
    }
}


class Second {
    private ArrayList<Line> lines = new ArrayList<Line>();
    private ArrayList<Point> points = new ArrayList<Point>();
    private boolean judge=false;
    Second(ArrayList<Point> ps){
        this.points=ps;
    }
    
    public void work() {
        for(int i=0;i<points.size();i++) {
            addLine(points.get(i),points.get((i+1)%5));
        }    
        JudgePentagon a=new JudgePentagon(lines,points);
        if(a.Judge()) {
            judge=true;
        }
        if(judge) {
            if(a.JudgeConvexity()) {
                System.out.print("true ");
                double circumference=lines.get(0).getLgenth()+lines.get(1).getLgenth()+lines.get(2).getLgenth()+lines.get(3).getLgenth()+lines.get(4).getLgenth();
                DecimalFormat x1 = new DecimalFormat("#####.0##");
                System.out.print(x1.format(circumference)+" ");
                double area=area(points.get(0),points.get(1),points.get(2))+area(points.get(0),points.get(2),points.get(3))+area(points.get(0),points.get(3),points.get(4));
                System.out.print(x1.format(area));
            }
            else System.out.print("false");
        }
        else System.out.print("not a pentagon");
    }
    
    public void addLine(Point p1,Point p2) {
        this.lines.add(new Line(p1,p2));
    }
    public double area(Point p1,Point p2,Point p3) {
        double s=Math.abs(p1.getX()*p2.getY()+p2.getX()*p3.getY()+p3.getX()*p1.getY()-p1.getX()*p3.getY()-p2.getX()*p1.getY()-p3.getX()*p2.getY())/2;
        return s;
    }
}

class Third {
    private ArrayList<Point> points = new ArrayList<Point>();
    Third(ArrayList<Point> ps){
        this.points=ps;
    }
    public void work() {
        if(points.get(0).equals(points.get(1))) {
            System.out.print("points coincide");
        }
        else {
            System.out.print("2 10.5 13.5");
        }
    }
}

View Code

分析报告：

7-1 点与线（类设计）

设计一个类表示平面直角坐标系上的点Point，私有属性分别为横坐标x与纵坐标y，数据类型均为实型数，除构造方法以及属性的getter与setter方法外，定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息，格式如下：(x,y)，数值保留两位小数。为简化题目，其中，坐标点的取值范围设定为(0,200]。若输入有误，系统则直接输出Wrong Format
设计一个类表示平面直角坐标系上的线Line，私有属性除了标识线段两端的点point1、point2外，还有一个字符串类型的color，用于表示该线段的颜色，同样，除构造方法以及属性的getter与setter方法外，定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息，输出格式如下：
```
  ```
      The line's color is:颜色值
      The line's begin point's Coordinate is:
      (x1,y1)
      The line's end point's Coordinate is:
      (x2,y2)
      The line's length is:长度值
  ```
```
其中，所有数值均保留两位小数，建议可用String.format("%.2f", data)方法。
```
  设计类图如下图所示。
```

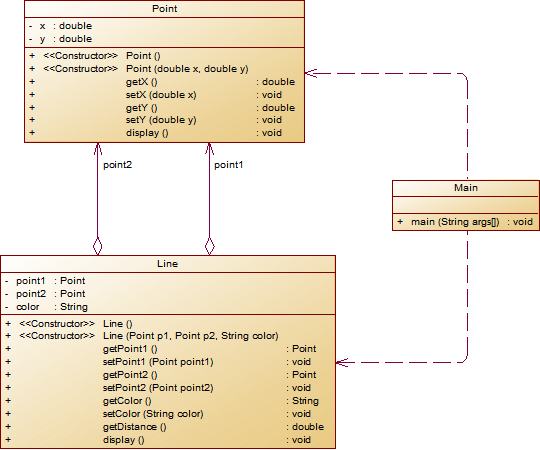
1641304523(1).jpg

** 题目要求：在主方法中定义一条线段对象，从键盘输入该线段的起点坐标与终点坐标以及颜色，然后调用该线段的display()方法进行输出。**

以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭

输入格式:

分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色，中间可用一个或多个空格、tab或者回车分隔。

输出格式:

The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值

输入样例1:

在这里给出一组输入。例如：

5
9.4
12.3
84
Red

输出样例1:

在这里给出相应的输出。例如：

The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96

输入样例2:

在这里给出一组输入。例如：

80.2356
352.12
24.5
100
Black

输出样例2:

在这里给出相应的输出。例如：

Wrong Format


源代码：

import java.util.Scanner;
class Point{
private double x;
private double y;
public Point() {
}
public Point(double x, double y) {
this.x = x;
this.y = y;
}
public double getX() {
return x;
}
public void setX(double x) {
this.x = x;
}
public double getY() {
return y;
}
public void setY(double y) {
this.y = y;
}
void display(){
System.out.println(String.format("(%.2f,%.2f)",this.x,this.y));
}
}
class Line{
private Point point1;
private Point point2;
private String color;
public Line() {
}
public Line(Point point1, Point point2, String color) {
this.point1 = point1;
this.point2 = point2;
this.color = color;
}
public Point getPoint1() {
return point1;
}
public void setPoint1(Point point1) {
this.point1 = point1;
}
public Point getPoint2() {
return point2;
}
public void setPoint2(Point point2) {
this.point2 = point2;
}
public String getColor() {
return color;
}
public void setColor(String color) {
this.color = color;
}
public double getDistance(){
double d=Math.sqrt(Math.pow((point1.getX()-point2.getX()),2)+Math.pow((point1.getY()-point2.getY()),2));
return d;
}
public void display(){
System.out.println("The line's color is:"+getColor());
System.out.println("The line's begin point's Coordinate is:");
point1.display();
System.out.println("The line's end point's Coordinate is:");
point2.display();
System.out.println("The line's length is:"+String.format("%.2f", getDistance()));
}
}
public class Main {
public static void main(String[] args) {
Scanner in=new Scanner(System.in);
double x1,x2,y1,y2;
String color;
x1=in.nextDouble();
y1=in.nextDouble();
x2=in.nextDouble();
y2=in.nextDouble();
color=in.next();
if(check(x1)&&check(x2)&&check(y1)&&check(y2)){
Point point1=new Point(x1,y1);
Point point2=new Point(x2,y2);
Line line=new Line(point1,point2,color);
line.display();
}else{
System.out.println("Wrong Format");
}
}
public static boolean check(double x){
if(x<=0||x>200){
return false;
}else{
return true;
}
}
}

View Code

分析报告：

7-2 点线面问题重构（继承与多态）

在“点与线（类设计）”题目基础上，对题目的类设计进行重构，以实现继承与多态的技术性需求。

对题目中的点Point类和线Line类进行进一步抽象，定义一个两个类的共同父类Element（抽象类），将display()方法在该方法中进行声明（抽象方法），将Point类和Line类作为该类的子类。
再定义一个Element类的子类面Plane，该类只有一个私有属性颜色color，除了构造方法和属性的getter、setter方法外，display()方法用于输出面的颜色，输出格式如下：The Plane's color is:颜色
在主方法内，定义两个Point（线段的起点和终点）对象、一个Line对象和一个Plane对象，依次从键盘输入两个Point对象的起点、终点坐标和颜色值（Line对象和Plane对象颜色相同），然后定义一个Element类的引用，分别使用该引用调用以上四个对象的display()方法，从而实现多态特性。示例代码如下：
```
      element = p1;//起点Point
      element.display();
      
      element = p2;//终点Point
      element.display();
      
      element = line;//线段
      element.display();
      
      element = plane;//面
      element.display();
```
类结构如下图所示。

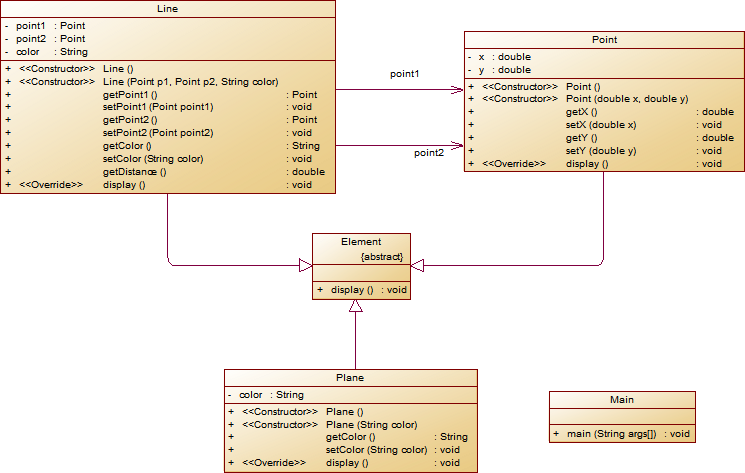
1641340607(1).jpg

其中，所有数值均保留两位小数，建议可用String.format("%.2f", data)方法。

以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭

输入格式:

分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色，中间可用一个或多个空格、tab或者回车分隔。

输出格式:

(x1,y1)
(x2,y2)
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值
The Plane's color is:颜色值

输入样例1:

在这里给出一组输入。例如：

5
9.4
12.3
84
Red

输出样例1:

在这里给出相应的输出。例如：

(5.00,9.40)
(12.30,84.00)
The line's color is:Red
The line's begin point's Coordinate is:
(5.00,9.40)
The line's end point's Coordinate is:
(12.30,84.00)
The line's length is:74.96
The Plane's color is:Red

输入样例2:

在这里给出一组输入。例如：

5
9.4
12.3
845
Black

输出样例2:

在这里给出相应的输出。例如：

Wrong Format



源代码：

import java.util.Scanner;
abstract class Element{
abstract void display();
}
class Point extends Element {
private double x;
private double y;

public Point() {
}

public Point(double x, double y) {
this.x = x;
this.y = y;
}

public double getX() {
return x;
}

public void setX(double x) {
this.x = x;
}

public double getY() {
return y;
}

public void setY(double y) {
this.y = y;
}
void display(){
System.out.println(String.format("(%.2f,%.2f)",this.x,this.y));
}
}
class Line extends Element{
private Point point1;
private Point point2;
private String color;

public Line() {
}
public Line(Point point1, Point point2, String color) {
this.point1 = point1;
this.point2 = point2;
this.color = color;
}

public Point getPoint1() {
return point1;
}

public void setPoint1(Point point1) {
this.point1 = point1;
}

public Point getPoint2() {
return point2;
}

public void setPoint2(Point point2) {
this.point2 = point2;
}

public String getColor() {
return color;
}

public void setColor(String color) {
this.color = color;
}
public double getDistance(){
double d=Math.sqrt(Math.pow((point1.getX()-point2.getX()),2)+Math.pow((point1.getY()-point2.getY()),2));
return d;
}
public void display(){
System.out.println("The line's color is:"+getColor());
System.out.println("The line's begin point's Coordinate is:");
point1.display();
System.out.println("The line's end point's Coordinate is:");
point2.display();
System.out.println("The line's length is:"+String.format("%.2f", getDistance()));
}
}
class Plane extends Element{
private String color;

public Plane() {
}

public Plane(String color) {
this.color = color;
}

public String getColor() {
return color;
}

public void setColor(String color) {
this.color = color;
}


void display() {
System.out.println("The Plane's color is:"+getColor());
}
}
public class Main {
public static void main(String[] args) {
Scanner in=new Scanner(System.in);
double x1,x2,y1,y2;
String color;
x1=in.nextDouble();
y1=in.nextDouble();
x2=in.nextDouble();
y2=in.nextDouble();
color=in.next();
if(check(x1)&&check(x2)&&check(y1)&&check(y2)){
Point point1=new Point(x1,y1);
Point point2=new Point(x2,y2);
Line line=new Line(point1,point2,color);
Plane plane=new Plane(color);
Element element;
element = point1;
element.display();
element = point2;
element.display();
element = line;
element.display();
element = plane;
element.display();
}else{
System.out.println("Wrong Format");
}
}
public static boolean check(double x){
if(x<=0||x>200){
return false;
}else{
return true;
}
}
}

View Code

分析报告：

7-3 点线面问题再重构（容器类）

在“点与线（继承与多态）”题目基础上，对题目的类设计进行重构，增加容器类保存点、线、面对象，并对该容器进行相应增、删、遍历操作。

在原有类设计的基础上，增加一个GeometryObject容器类，其属性为ArrayList<Element>类型的对象（若不了解泛型，可以不使用<Element>）
增加该类的add()方法及remove(int index)方法，其功能分别为向容器中增加对象及删除第index - 1（ArrayList中index>=0）个对象

在主方法中，用户循环输入要进行的操作（choice∈[0,4]），其含义如下：

1：向容器中增加Point对象
2：向容器中增加Line对象
3：向容器中增加Plane对象
4：删除容器中第index - 1个数据，若index数据非法，则无视此操作
0：输入结束

示例代码如下：

   choice = input.nextInt();
    while(choice != 0) {
        switch(choice) {
        case 1://insert Point object into list 
          ...
            break;
        case 2://insert Line object into list
            ...
            break;
        case 3://insert Plane object into list
            ...
            break;
        case 4://delete index - 1 object from list
            int index = input.nextInt();
            ...
        }
        choice = input.nextInt();
    }

输入结束后，按容器中的对象顺序分别调用每个对象的display()方法进行输出。
类图如下所示：

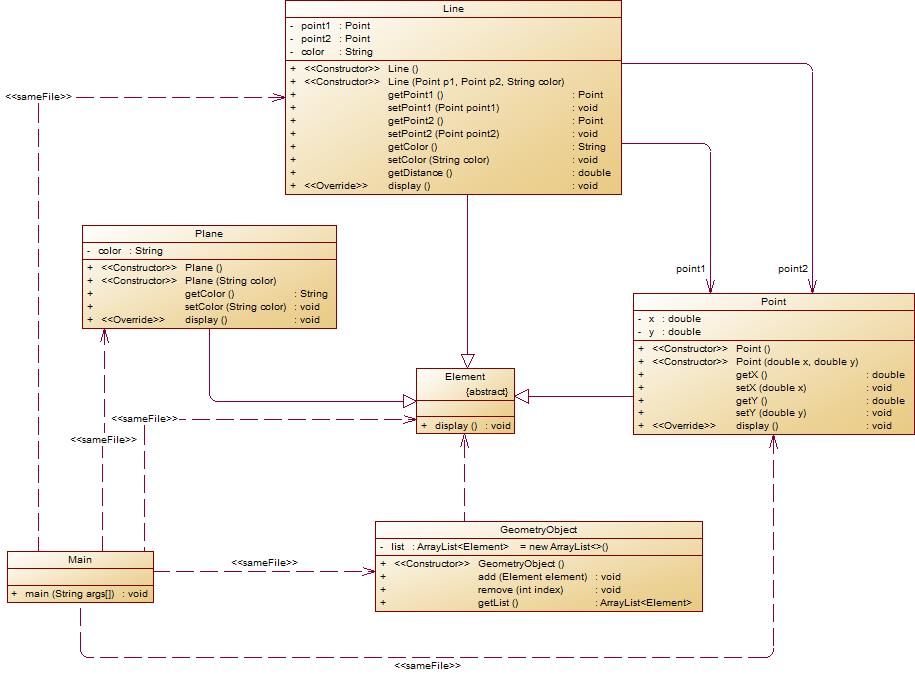
以下情况为无效作业
- 无法运行
- 设计不符合所给类图要求
- 未通过任何测试点测试
- 判定为抄袭

输入格式:

switch(choice) {
            case 1://insert Point object into list 
              输入“点”对象的x，y值
                break;
            case 2://insert Line object into list
                输入“线”对象两个端点的x，y值
                break;
            case 3://insert Plane object into list
                输入“面”对象的颜色值
                break;
            case 4://delete index - 1 object from list
                输入要删除的对象位置（从1开始）
                ...
            }

输出格式:

Point、Line、Plane的输出参考题目2
删除对象时，若输入的index超出合法范围，程序自动忽略该操作

输入样例:

在这里给出一组输入。例如：

1
3.4
5.6
2
4.4
8.0
0.98
23.888
Red
3
Black
1
9.8
7.5
3
Green
4
3
0

输出样例:

在这里给出相应的输出。例如：

(3.40,5.60)
The line's color is:Red
The line's begin point's Coordinate is:
(4.40,8.00)
The line's end point's Coordinate is:
(0.98,23.89)
The line's length is:16.25
(9.80,7.50)
The Plane's color is:Green


心得：不够熟练，最后没做。

本题共使用了六个类，其中Main类为其主类，Element类为多个类的父类。此程序中Main类结构最为复杂，多项数值都较为偏高，除此之外，大多类中的方法体都较多，但平均复杂度都较低，由此可见，大多方法结构都较为简单，并非十分合理。而后便是所有类中的注释都较少。

三、总结

通过本阶段的三次题目集，以及之后的总结，更好了理解了java中类、方法的设计，以及java中自带的各种方法，继承多态容器正则表达式类设计原则等，对于面向对象程序设计的概念理解又加深了许多。继承提高了类之间的耦合性(继承的缺点，耦合度高就会造成代码之间的联系越紧密，代码独立性越差)多态的好处：可以使程序有良好的扩展，并可以对所有类的对象进行通用处理。积累了一些debug的经验，深刻认识到了调试的重要性，学会了调试的基本技巧，如何设置断点，单步进入，跟踪参数，以及更改代码的逻辑顺序，排除逻辑错误，对提高代码的质量大有改善。

标签：getX,get,double,ps,BLOG,getY,public
From： https://www.cnblogs.com/20011211zqp/p/16839547.html

一、前言

二、设计与分析

输入格式:

输出格式:

输入样例1:

输出样例1:

输入样例2:

输出样例2:

输入格式:

输出格式:

输入样例1:

输出样例:

输入样例2:

输出样例:

输入样例3:

输出样例:

输入样例4:

输出样例:

输入样例5:

输出样例:

输入样例6:

输出样例:

输入样例7:

输出样例:

输入样例8:

输出样例:

输入样例9:

输出样例:

输入格式:

输出格式:

输入样例1:

输出样例:

输入格式:

输出格式:

输入样例:

输出样例:

输入格式:

输出格式:

输入样例1:

输出样例1:

输入样例2:

输出样例2:

输入格式:

输出格式:

输入样例1:

输出样例1:

输入样例2:

输出样例2:

输入格式:

输出格式:

输入样例:

输出样例:

三、总结

相关文章

赞助商

阅读排行