JAVA题目集4、5及期中考试总结Blog

标签：JAVA Point 期中考试 double return System Blog inline new

一、前言

题目集四：

知识点：类的应用，正则表达式，面向对象思想，四边形的一些知识点。

题量：适中。

难度：比较难。

题目集五：

知识点：类的应用，面向对象的思想，正则表达式，五边形的有关知识。

题量：较少。

难度：难。

期中考试：

知识点：类的应用，继承和多态的使用，抽象的使用。

题量：适中。

难度：适中。

二、设计与分析

 题目集四：

7-1 sdut-String-2 识蛟龙号载人深潜，立科技报国志（II）（正则表达式）

背景简介：

“蛟龙号”载人深潜器是我国首台自主设计、自主集成研制的作业型深海载人潜水器，设计最大下潜深度为7000米级，也是目前世界上下潜能力最强的作业型载人潜水器。“蛟龙号”可在占世界海洋面积99.8%的广阔海域中使用，对于我国开发利用深海的资源有着重要的意义。

中国是继美、法、俄、日之后世界上第五个掌握大深度载人深潜技术的国家。在全球载人潜水器中，“蛟龙号”属于第一梯队。目前全世界投入使用的各类载人潜水器约90艘，其中下潜深度超过1000米的仅有12艘，更深的潜水器数量更少，目前拥有6000米以上深度载人潜水器的国家包括中国、美国、日本、法国和俄罗斯。除中国外，其他4国的作业型载人潜水器最大工作深度为日本深潜器的6527米，因此“蛟龙号”载人潜水器在西太平洋的马里亚纳海沟海试成功到达7020米海底，创造了作业类载人潜水器新的世界纪录。

从2009年至2012年，蛟龙号接连取得1000米级、3000米级、5000米级和7000米级海试成功。下潜至7000米，说明蛟龙号载人潜水器集成技术的成熟，标志着我国深海潜水器成为海洋科学考察的前沿与制高点之一。

2012年6月27日11时47分，中国“蛟龙”再次刷新“中国深度”——下潜7062米。6月3日，“蛟龙”出征以来，已经连续书写了5个“中国深度”新纪录：6月15日，6671米；6月19日，6965米；6月22日，6963米；6月24日，7020米；6月27日，7062米。下潜至7000米，标志着我国具备了载人到达全球99%以上海洋深处进行作业的能力，标志着“蛟龙”载人潜水器集成技术的成熟，标志着我国深海潜水器成为海洋科学考察的前沿与制高点之一，标志着中国海底载人科学研究和资源勘探能力达到国际领先水平。

‘蛟龙’号是我国载人深潜发展历程中的一个重要里程碑。它不只是一个深海装备，更代表了一种精神，一种不畏艰险、赶超世界的精神，它是中华民族进军深海的号角。

了解蛟龙号”载人深潜器“的骄人业绩，为我国海底载人科学研究和资源勘探能力达到国际领先水平而自豪，小伙伴们与祖国同呼吸、共命运，一定要学好科学文化知识、提高个人能力，增强创新意识，做事精益求精，立科技报国之志！

请编写程序，实现如下功能：读入关于蛟龙号载人潜水器探测数据的多行字符串，从给定的信息找出数字字符，输出每行的数字之和。

提示 若输入为“2012年2月”，则该行的输出为：2014。若干个连续的数字字符作为一个整体，以十进制形式相加。

输入格式:

读入关于蛟龙号载人潜水器探测数据的多行字符串，每行字符不超过80个字符。

以"end"结束。

输出格式:

与输入行相对应的各个整数之和。

主要代码：

import java.util.Scanner;
public class Main{
   public static void main(String[] args){
        Scanner str=new Scanner(System.in);
        String s=str.nextLine();
        while(!s.equals("end")){
            String []S=s.split("\\D+");
            int sum=0;
            for(int i=0;i<S.length;i++){
                if(!S[i].equals(""))//当时误写成S。equals("")答案错误!!!
                    sum+=(int) Integer.parseInt(S[i]);
            }
            System.out.println(sum);
            s=str.nextLine();
        }
   }
}

View Code

代码思路：接受输入，将输入的每一行字符串根据是否为数字截取到数组，然后将这些数字相加输出，难度不大，主要要掌握一些基本的语法。

7-2 点线形系列4-凸四边形的计算

用户输入一组选项和数据，进行与四边形有关的计算。
以下四边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入四个点坐标，判断是否是四边形、平行四边形，判断结果输出true/false，结果之间以一个英文空格符分隔。
2：输入四个点坐标，判断是否是菱形、矩形、正方形，判断结果输出true/false，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
3：输入四个点坐标，判断是凹四边形（false）还是凸四边形(true)，输出四边形周长、面积，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
4：输入六个点坐标，前两个点构成一条直线，后四个点构成一个四边形或三角形，输出直线与四边形（也可能是三角形）相交的交点数量。如果交点有两个，再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积（不换行）。若直线与四边形或三角形的一条边线重合，输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入，输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况：假设三角形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z 不与xy都相邻，如z x y s、x z s y、x s z y
5：输入五个点坐标，输出第一个是否在后四个点所构成的四边形（限定为凸四边形，不考虑凹四边形）或三角形（判定方法见选项4）的内部（若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。如果点在多边形的某条边上，输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形，输出"not a quadrilateral or triangle"。

输入格式:

基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

输出格式:

基本输出格式见每种选项的描述。
异常情况输出：
如果不符合基本格式，输出"Wrong Format"。
如果符合基本格式，但输入点的数量不符合要求，输出"wrong number of points"。
注意：输出的数据若小数点后超过3位，只保留小数点后3位，多余部分采用四舍五入规则进到最低位。小数点后若不足3位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333，1.0按格式输出为1.0

选项1、2、3中，若四边形四个点中有重合点，输出"points coincide"。
选项4中，若前两个输入线的点重合，输出"points coincide"。

代码思路：首先创建类，包括四边形的类，三角行的类，点、线的类，代码及圈复杂度如下，再根据题目要求进行四边形相关的具体操作，调用各个类的方法进行解答。

点类：

public class Point {
        double x,y;
        public Point(double a,double b){
            this.x=a;
            this.y=b;
        }
        public double getx(){
            return x;
        }
        public double gety(){
            return y;
        }
        public double juli(Point p){
            return Math.sqrt((this.x-p.x )*(this.x-p.x )+(this.y-p.y )*(this.y-p.y));
        }
        public double xilv(Point p){
            if(this.x==p.x){
                System.out.println("Slope does not exist");
                System.exit(0);
            }
            return (this.y-p.y)/(this.x-p.x);
        }


}

View Code

圈复杂度分析：

线类：

import static java.lang.Math.max;
import static java.lang.Math.min;

public class Line {
    Point x,y;

    Line (Point a, Point b){
        this.x=a;
        this.y=b;

    }
    //长度
    double length(){
        return this.x.juli(this.y);
    }
    //点到直线的距离
    double distance(Point p){//!!!
        if(this.x.x==this.y.x){
            return  (p.x-this.x.x);

        }
        else{
            double e=(this.x.y-this.y.y)/(this.x.x-this.y.x);
            double b=this.x.y-(e*this.x.x);
            return (e*p.x-p.y+b)/Math.sqrt(e*e+1);
        }
    }
    //两条直线是否相交
    public static boolean intersect(double l1x1,double l1y1,double l1x2,double l1y2,double l2x1,double l2y1,double l2x2,double l2y2) {

        // 快速排斥实验 首先判断两条线段在 x 以及 y 坐标的投影是否有重合。 有一个为真，则代表两线段必不可交。
        if (Math.max(l1x1,l1x2) < Math.min(l2x1 ,l2x2)
                || Math.max(l1y1,l1y2) < Math.min(l2y1,l2y2)
                || Math.max(l2x1,l2x2) < Math.min(l1x1,l1x2)
                || Math.max(l2y1,l2y2) < Math.min(l1y1,l1y2))
        {
            return false;
        }
        // 跨立实验  如果相交则矢量叉积异号或为零，大于零则不相交
        else if ((((l1x1 - l2x1) * (l2y2 - l2y1) - (l1y1 - l2y1) * (l2x2 - l2x1))
                * ((l1x2 - l2x1) * (l2y2 - l2y1) - (l1y2 - l2y1) * (l2x2 - l2x1))) > 0
                || (((l2x1 - l1x1) * (l1y2 - l1y1) - (l2y1 - l1y1) * (l1x2 - l1x1))
                * ((l2x2 - l1x1) * (l1y2 - l1y1) - (l2y2 - l1y1) * (l1x2 - l1x1))) > 0)
        {
            return false;
        }
        return true;
    }
    //多边形的对角线
    public double duijiaoxian() {
        double duijiaoxian=Math.sqrt((this.x.x-this.y.x)*(this.x.x-this.y.x)+(this.x.y-this.y.y)*(this.x.y-this.y.y));
        return duijiaoxian;
    }
    //线重合
    public boolean xianchonghe (Line l){
        return this.pingxing(l)&&l.distance(this.x)==0;
    }
    //点在线上的判断
    boolean inline(Point p){
        if(this.x.x==this.y.x&&this.y.x==p.x)
            return true;
        double e=(this.x.y-this.y.y)/(this.x.x-this.y.x);
        double b=this.x.y-(e*this.x.x);
        if((e*p.x-p.y+b)==0)
            return true;
        else
            return false;
    }
    //交点
     public Point jiaodian(Line l){
        Point v=sub(l.y,l.x);
        Point w=sub(this.y,this.x);
        Point p=l.x;
        Point q=this.x;
        Point u=sub(p,q);
        double t=cross(w,u)/cross(v,w);
        Point ans =new Point( p.x+v.x*t,p.y+v.y*t);
        ans.x=p.x+v.x*t;ans.y=p.y+v.y*t;
        double y0=ans.y;
        double x0=ans.x;
        if(((x0)>=min(x.x,y.x)&&(x0)<=max(x.x,y.x))&&((y0)>=min(x.y,y.y)&&(y0)<=max(x.y,y.y)))
            return ans;
        return null;

    }
    public static double cross (Point a, Point b){
        return a.x*b.y-a.y*b.x;
    }
    public static Point sub(Point a, Point b){
        return new Point(a.x-b.x,a.y-b.y);
    }
//平行判断
    boolean pingxing  (Line a){
        if((a.x.x==a.y.x )&&(this.x.x==this.y.x))
            return true;
        if((a.x.x==a.y.x)&&(this.x.x!=this.y.x))
            return false;
        if((a.x.x!=a.y.x)&&(this.x.x==this.y.x))
            return false;
        double e=a.x.xilv(a.y);
        double e1=this.x.xilv(this.y);
        if(e==e1)
            return true;
        else return false;
    }

}

View Code

圈复杂度分析：

三角形类：

import java.util.Arrays;

public class Sanjiao {
    Main.Point sx,sy,sz;
    Main.Line sa,sb,sc;
    Sanjiao (Main.Point a, Main.Point b, Main.Point c){
        this.sx=a;
        this.sy=b;
        this.sz=c;
        this.sa=new Main.Line(b,c);
        this.sb=new Main.Line(a,c);
        this.sc=new Main.Line(a,b);
    }
    //判断能否构成三角形
    public boolean gouchengsanjiao(){
        if(((this.sa.length()+this.sb.length())<=this.sc.length())||((this.sa.length()+this.sc.length())<=this.sb.length())||((this.sb.length()+this.sc.length())<=this.sa.length())){
            return true;
        }
        else return false;
    }
//周长
    public double zhouchang(){
        return (this.sa.length()+this.sb.length()+this.sc.length());
    }
    //面积
    public double mianji(){
        double area=0;
        double s=(this.sa.length()+this.sb.length()+this.sc.length())/2;
        return area=Math.sqrt(s*(s-this.sa.length())*(s-this.sb.length())*(s-this.sc.length()));
    }
    //判断三角形的类型
    public boolean insanjiao(Main.Point p){
        Main.Sanjiao san1=new Main.Sanjiao(p,sx,sy);
        Main.Sanjiao san2=new Main.Sanjiao(p,sy,sz);
        Main.Sanjiao san3=new Main.Sanjiao(p,sz,sx);
        double m1=san1.mianji();
        double m2=san2.mianji();
        double m3=san3.mianji();
        if(Math.abs(this.mianji()-(m1+m2+m3))<0.0001)
            return true;
        else return false;
    }
    //分割三角形
    public void fengesanjiaoxing(Main.Line l){
        double area1=0,area2=0;
        if(this.sc.jiaodian(l)!=null&&this.sa.jiaodian(l)!=null&&this.sc.jiaodian(l)!=this.sa.jiaodian(l)){
            Main.Sanjiao ss1=new Main.Sanjiao(this.sc.jiaodian(l),this.sy,this.sa.jiaodian(l));
            area1=ss1.mianji();
            area2=this.mianji()-area1;
            double mj1=outformat( area1);
            double mj2=outformat( area2);
            out(mj1,mj2);
        }
        else if(this.sc.jiaodian(l)!=null&&this.sb.jiaodian(l)!=null&&this.sc.jiaodian(l)!=this.sb.jiaodian(l)){
            Main.Sanjiao ss1=new Main.Sanjiao(this.sc.jiaodian(l),this.sb.jiaodian(l),this.sx);
            area1=ss1.mianji();
            area2=this.mianji()-area1;
            double mj1=outformat( area1);
            double mj2=outformat( area2);
            out(mj1,mj2);
        }
        else if(this.sa.jiaodian(l)!=null&&this.sb.jiaodian(l)!=null&&this.sa.jiaodian(l)!=this.sb.jiaodian(l)){
            Main.Sanjiao ss1=new Main.Sanjiao(this.sa.jiaodian(l),this.sz,this.sb.jiaodian(l));
            area1=ss1.mianji();
            area2=this.mianji()-area1;
            double mj1=outformat( area1);
            double mj2=outformat( area2);
            out(mj1,mj2);
        }
        else {
            System.out.println(0);
            System.exit(0);
        }
    }
    public Double outformat(double num) {
        if(num*1e+3%10!=0) {
            String num1=String.format("%.3f",num);
            return Double.valueOf(num1);
        }
        return num;
    }
    //输出线段和三角形的交点个数及其围成的面积
    public void out(double m1,double m2){
        if(m1>=m2){
            System.out.println(2+" "+m2+" "+m1);
            System.exit(0);
        }
        else{
            System.out.println(2+" "+m1+" "+m2);
            System.exit(0);
        }
    }
    //判断线段和三角形的边重合
    public boolean bianchonghe(Main.Line l){
        if(this.sa.xianchonghe(l))
            return false;
        else if(this.sb.xianchonghe(l))
            return false;
        else if(this.sc.xianchonghe(l))
            return  false;
        else
            return true;
    }
}

View Code

圈复杂度分析：

四边形类：

public class Sibian {
    Main.Point a,b,c,d;
    Main.Line ab,bc,cd,da,ac,bd;
    private boolean judge1=false;//0,2
    private boolean judge2=false;//1,3
    Sibian(Main.Point a, Main.Point b, Main.Point c, Main.Point d){
        this.a=a;this.b=b;this.c=c;this.d=d;
        this.ab=new Main.Line(a,b);
        this.bc=new Main.Line(b,c);
        this.cd=new Main.Line(c,d);
        this.da=new Main.Line(d,a);
        this.ac=new Main.Line(a,c);
        this.bd=new Main.Line(b,d);
    }
    public void sibianxing(){
        if(Math.abs((a.y-c.y)*(a.x-b.x)-(a.y-b.y)*(a.x-c.x))<1e-6||
                Math.abs((a.y-d.y)*(a.x-b.x)-(a.y-b.y)*(a.x-d.x))<1e-6||
                Math.abs((a.y-d.y)*(a.x-c.x)-(a.y-c.y)*(a.x-d.x))<1e-6||
                Math.abs((b.y-d.y)*(b.x-c.x)-(b.y-c.y)*(b.x-d.x))<1e-6)System.out.print("false ");
        else {
            if(!Main.Line.intersect(a.x,a.y,d.x,d.y,b.x,b.y,c.x,c.y)) {
                System.out.print("true ");
            }
            else System.out.print("false ");
        }
    }
    //平行四边形
    public void pingxingsibianxing(){
        if(this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length())System.out.print("true");
        else System.out.print("false");
    }
    //判断能否构成四边形
    public boolean nengfougoucheng(){
        if(Math.abs((a.y-c.y)*(a.x-b.x)-(a.y-b.y)*(a.x-c.x))<1e-6||
                Math.abs((a.y-d.y)*(a.x-b.x)-(a.y-b.y)*(a.x-d.x))<1e-6||
                Math.abs((a.y-d.y)*(a.x-c.x)-(a.y-c.y)*(a.x-d.x))<1e-6||
                Math.abs((b.y-d.y)*(b.x-c.x)-(b.y-c.y)*(b.x-d.x))<1e-6) {
            return false;
        }
        else return !Main.Line.intersect(a.x, a.y, d.x, d.y, b.x, b.y, c.x, c.y) && !Main.Line.intersect(a.x, a.y, b.x, b.y, d.x, d.y, c.x, c.y);
    }
    //菱形
    public boolean lingxing(){
        return (this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length());
    }
    //长方形
    public boolean changfangxing(){
        Main.Line l1=new Main.Line(a,c);
        double ac=l1.duijiaoxian();
        Main.Line l2=new Main.Line(b,d);
        double bd=l2.duijiaoxian();
        return (ac==bd&&this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length());
    }

    public boolean zhengfangxing(){
        return (lingxing()&& changfangxing());
    }
    //凸四边形判断
    public boolean otupanduan() {
        Main.Line l1=new Main.Line(a,c);
        double distance1=l1.distance(b);
        double distance2=l1.distance(d);
        Main.Line l2=new Main.Line(b,d);
        double distance3=l2.distance(a);
        double distance4= l2.distance(c);
        if(distance1*distance2<0)judge1=true;
        if(distance3*distance4<0)judge2=true;
        if(judge1==true&&judge2==true) {
            return true;
        }
        return false;
    }
    //周长
    public double zhouchang() {
        double ab=this.ab.length();
        double bc=this.bc.length();
        double cd=this.cd.length();
        double da=this.da.length();
        double c=ab+bc+cd+da;
        double C=outformat(c);
        return C;
    }
    //面积
    public double area() {
        double area=0;
        double area1=0;
        double area2=0;
        double are=0;
        //凸四边形
        if(judge1==true&&judge2==true) {
            area1=Math.abs((b.x*c.y+c.x*d.y+d.x*b.y-b.x*d.y-c.x*b.y-d.x*c.y)/2);
            area2=Math.abs((b.x*a.y+a.x*d.y+d.x*b.y-b.x*d.y-a.x*b.y-d.x*a.y)/2);
            area=area1+area2;
            are= outformat(area);
        }
        else if(judge1==false) {
            area1=Math.abs((b.x*d.y+d.x*a.y+a.x*b.y-b.x*a.y-d.x*b.y-a.x*d.y)/2);
            area2=Math.abs((d.x*c.y+c.x*b.y+b.x*d.y-d.x*b.y-c.x*d.y-b.x*c.y)/2);
            area=area1+area2;
            are= outformat(area);
        }
        else if(judge2==false) {
            area1=Math.abs((b.x*c.y+c.x*a.y+a.x*b.y-b.x*a.y-c.x*b.y-a.x*c.y)/2);
            area2=Math.abs((d.x*c.y+c.x*a.y+a.x*d.y-d.x*a.y-c.x*d.y-a.x*c.y)/2);
            area=area1+area2;
            are=outformat(area);
        }
        return are;
    }
    //符合题目的输出
    public Double outformat(double num) {
        if(num*1e+3%10!=0) {
            String num1=String.format("%.3f",num);
            return Double.valueOf(num1);
        }
        return num;
    }
    //判断边与线段是否重合
    public boolean bianchonghe (Main.Line l){
        if(this.ab.xianchonghe(l)){
            return true;
        }
        else if(this.bc.xianchonghe(l)){
            return true;
        }
        else if(this.cd.xianchonghe(l)){
            return true;
        }
        else if(this.da.xianchonghe(l)){
            return true;
        }
        return false;
    }
    //判断点是否在四边形中
    public boolean insibian(Main.Point p){
        double m=0;
        if(otupanduan()){
            m=area();
        }

        Main.Sanjiao ss1=new Main.Sanjiao(p,a,b);
        Main.Sanjiao ss2=new Main.Sanjiao(p,b,c);
        Main.Sanjiao ss3=new Main.Sanjiao(p,c,d);
        Main.Sanjiao ss4=new Main.Sanjiao(p,d,a);
        double m1=ss1.mianji();
        double m2=ss2.mianji();
        double m3=ss3.mianji();
        double m4=ss4.mianji();
        if(Math.abs(m-(m1+m2+m3+m4))<0.0001)/*注意一定要三位小数或更多，不然通不过测试点*/
            return true;
        else return false;
    }
    //分割四边形
    public void fengesibianxing(Main.Line l){
        double area1=0,area2=0;
        if(this.ac.xianchonghe(l)){
            Main.Sanjiao ss1=new Main.Sanjiao(this.a,this.b,this.c);
            area1=ss1.mianji();
            area2=this.area()-area1;
            double mj1= outformat(area1);
            double mj2= outformat(area2);
            out(mj1,mj2);
        }
        else if(this.bd.xianchonghe(l)){
            Main.Sanjiao ss1=new Main.Sanjiao(this.a,this.b,this.d);
            area1=ss1.mianji();
            area2=this.area()-area1;
            double mj1= outformat(area1);
            double mj2= outformat(area2);
            out(mj1,mj2);
        }
        else if(this.ab.jiaodian(l)!=null&&this.bc.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.bc.jiaodian(l)){
            Main.Sanjiao ss1=new Main.Sanjiao(this.ab.jiaodian(l),this.b,this.bc.jiaodian(l));
            area1=ss1.mianji();
            area2=this.area()-area1;
            double mj1= outformat(area1);
            double mj2= outformat(area2);
            out(mj1,mj2);
        }
        else if(this.ab.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null){
            Main.Sibian ss1=new Main.Sibian(this.a,this.ab.jiaodian(l),this.cd.jiaodian(l),this.d);
            area1=ss1.area();
            area2=this.area()-area1;
            double mj1= outformat(area1);
            double mj2= outformat(area2);
            out(mj1,mj2);
        }
        else if(this.ab.jiaodian(l)!=null&&this.da.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.da.jiaodian(l)){
            Main.Sanjiao ss1=new Main.Sanjiao(this.a,this.ab.jiaodian(l),this.da.jiaodian(l));
            area1=ss1.mianji();
            area2=this.area()-area1;
            double mj1= outformat(area1);
            double mj2= outformat(area2);
            out(mj1,mj2);
        }
        else if(this.bc.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null&&this.bc.jiaodian(l)!=this.cd.jiaodian(l)){
            Main.Sanjiao ss1=new Main.Sanjiao(this.bc.jiaodian(l),this.c,this.cd.jiaodian(l));
            area1=ss1.mianji();
            area2=this.area()-area1;
            double mj1= outformat(area1);
            double mj2= outformat(area2);
            out(mj1,mj2);
        }
        else if(this.bc.jiaodian(l)!=null&&this.da.jiaodian(l)!=null){
            Main.Sibian ss1=new Main.Sibian(this.a,this.b,this.bc.jiaodian(l),this.da.jiaodian(l));
            area1=ss1.area();
            area2=this.area()-area1;
            double mj1= outformat(area1);
            double mj2= outformat(area2);
            out(mj1,mj2);
        }
        else if(this.cd.jiaodian(l)!=null&&this.da.jiaodian(l)!=null&&this.da.jiaodian(l)!=this.cd.jiaodian(l)){
            Main.Sanjiao ss1=new Main.Sanjiao(this.da.jiaodian(l),this.d,this.cd.jiaodian(l));
            area1=ss1.mianji();
            area2=this.area()-area1;
            double mj1= outformat(area1);
            double mj2= outformat(area2);
            out(mj1,mj2);
        }
        else {
            System.out.println(0);
            System.exit(0);
        }
    }
    //输出线段与四边形的交点个数及交点围成的面积
    public void out(double m1,double m2){
        if(m1>=m2){
            System.out.println(2+" "+m2+" "+m1);
            System.exit(0);
        }
        else{
            System.out.println(2+" "+m1+" "+m2);
            System.exit(0);
        }
    }
}

View Code

圈复杂度分析：

主要代码：

import java.util.Arrays;
import java.util.Scanner;

import static java.lang.Math.max;
import static java.lang.Math.min;
import static java.lang.StrictMath.abs;

public class Main {
    public static void main(String[] args) {
        Scanner str=new Scanner(System.in);
        String s=str.nextLine();
        if (!geshi(s)) return;
        if (!dianshu(s)) return;
        String s1=s.substring(2);
        String []b=s1.split(",| ");
        int choice = s.charAt(0)-48;
        switch (choice){
            case 1:{
                double x1= Double.parseDouble(b[0]);double y1= Double.parseDouble(b[1]);
                double x2= Double.parseDouble(b[2]);double y2= Double.parseDouble(b[3]);
                double x3= Double.parseDouble(b[4]);double y3= Double.parseDouble(b[5]);
                double x4= Double.parseDouble(b[6]);double y4= Double.parseDouble(b[7]);
                Point point1= new Point();
                Point point2= new Point();
                Point point3 = new Point();
                Point point4 = new Point();
                point1.x=x1;point1.y=y1;
                point2.x=x2;point2.y=y2;
                point3.x=x3;point3.y=y3;
                point4.x=x4;point4.y=y4;
                if((x1==x2&&y1==y2)||(x1==x4&&y1==y4)|(x2==x3&&y2==y3)||(x3==x4&&y3==y4)||(x1==x3&&y1==y3)||(x2==x4&&y2==y4)){
                    System.out.println("points coincide");
                    return ;
                }

                Sibian S=new Sibian(point1,point2,point3,point4);
                S.sibianxing();
                S.pingxingsibianxing();
                break;
            }
            case 2:{
                double x1= Double.parseDouble(b[0]);double y1= Double.parseDouble(b[1]);
                double x2= Double.parseDouble(b[2]);double y2= Double.parseDouble(b[3]);
                double x3= Double.parseDouble(b[4]);double y3= Double.parseDouble(b[5]);
                double x4= Double.parseDouble(b[6]);double y4= Double.parseDouble(b[7]);
                Point point1= new Point();
                Point point2= new Point();
                Point point3 = new Point();
                Point point4 = new Point();
                point1.x=x1;point1.y=y1;
                point2.x=x2;point2.y=y2;
                point3.x=x3;point3.y=y3;
                point4.x=x4;point4.y=y4;
                if((x1==x2&&y1==y2)||(x1==x4&&y1==y4)|(x2==x3&&y2==y3)||(x3==x4&&y3==y4)){
                    System.out.println("points coincide");
                    return ;
                }
                Sibian S=new Sibian(point1,point2,point3,point4);
                if(!S.nengfougoucheng()){
                    System.out.print("not a quadrilateral");
                    System.exit(0);
                }
                System.out.println(S.lingxing()+" "+S.changfangxing()+" "+S.zhengfangxing());
                break;
            }
            case 3: {
                double x1 = Double.parseDouble(b[0]);double y1 = Double.parseDouble(b[1]);
                double x2 = Double.parseDouble(b[2]);double y2 = Double.parseDouble(b[3]);
                double x3 = Double.parseDouble(b[4]);double y3 = Double.parseDouble(b[5]);
                double x4 = Double.parseDouble(b[6]);double y4 = Double.parseDouble(b[7]);
                Point point1 = new Point();
                Point point2 = new Point();
                Point point3 = new Point();
                Point point4 = new Point();
                point1.x = x1;point1.y = y1;
                point2.x = x2;point2.y = y2;
                point3.x = x3;point3.y = y3;
                point4.x = x4;point4.y = y4;
                if ((x1==x2&&y1==y2)||(x1==x4&&y1==y4)|(x2==x3&&y2==y3)||(x3==x4&&y3==y4)) {
                    System.out.println("points coincide");
                    return;
                }
                Sibian S = new Sibian(point1, point2, point3, point4);
                if(!S.nengfougoucheng()){
                    System.out.print("not a quadrilateral");
                    System.exit(0);
                }

                System.out.print(S.otupanduan()+" "+S.zhouchang()+" "+S.area());
                break;
            }
            case 4: {
                double x1 = Double.parseDouble(b[0]);double y1 = Double.parseDouble(b[1]);
                double x2 = Double.parseDouble(b[2]);double y2 = Double.parseDouble(b[3]);
                double x3 = Double.parseDouble(b[4]);double y3 = Double.parseDouble(b[5]);
                double x4 = Double.parseDouble(b[6]);double y4 = Double.parseDouble(b[7]);
                double x5 = Double.parseDouble(b[8]);double y5 = Double.parseDouble(b[9]);
                double x6 = Double.parseDouble(b[10]);double y6 = Double.parseDouble(b[11]);
                Point point1 = new Point();
                Point point2 = new Point();
                Point point3 = new Point();
                Point point4 = new Point();
                Point point5 = new Point();
                Point point6 = new Point();
                point1.x = x1;point1.y = y1;
                point2.x = x2;point2.y = y2;
                point3.x = x3;point3.y = y3;
                point4.x = x4;point4.y = y4;
                point5.x = x5;point5.y = y5;
                point6.x = x6;point6.y = y6;
                if ((x1 == x2 && y1 == y2) ) {
                    System.out.println("points coincide");
                    return;
                }
                Line l=new Line(point1,point2);
                Sibian S = new Sibian(point3, point4, point5, point6);
                if(S.nengfougoucheng()){
                    if(S.bianchonghe(l)){

                        System.out.println("The line is coincide with one of the lines");
                        return;}
                    int sum=S.fengesibainxing(l);
                    System.out.println(sum);
                    return;
                }

                System.out.println("not a quadrilateral or triangle");
                break;
            }
            case 5: {
                double x1 = Double.parseDouble(b[0]);double y1 = Double.parseDouble(b[1]);
                double x2 = Double.parseDouble(b[2]);double y2 = Double.parseDouble(b[3]);
                double x3 = Double.parseDouble(b[4]);double y3 = Double.parseDouble(b[5]);
                double x4 = Double.parseDouble(b[6]);double y4 = Double.parseDouble(b[7]);
                double x5 = Double.parseDouble(b[8]);double y5 = Double.parseDouble(b[9]);

                Point point1 = new Point();
                Point point2 = new Point();
                Point point3 = new Point();
                Point point4 = new Point();
                Point point5 = new Point();

                point1.x = x1;point1.y = y1;
                point2.x = x2;point2.y = y2;
                point3.x = x3;point3.y = y3;
                point4.x = x4;point4.y = y4;
                point5.x = x5;point5.y = y5;
                Sibian S = new Sibian(point2, point3, point4, point5);
                if(S.nengfougoucheng()){
                    if(S.ab.inline(point1)||S.bc.inline(point1)||S.cd.inline(point1)||S.da.inline(point1)){
                        System.out.println("on the quadrilateral");
                        return;
                    }
                    else if(S.insibian(point1)){
                        System.out.println("in the quadrilateral");
                        return;
                    }
                    else {
                        System.out.println("outof the quadrilateral");
                        return;
                    }
                }
                else{
                    if(S.ac.inline(point3)){
                        Sanjiao ss1=new Sanjiao(point2,point4,point5);
                        if(ss1.sa.inline(point1)||ss1.sb.inline(point1)||ss1.sc.inline(point1)){
                            System.out.println("on the triangle");
                            return;
                        }
                        else if(ss1.insanjiao(point1)){
                            System.out.println("in the triangle");
                            return;
                        }
                        else{
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                    else if(S.ac.inline(point5)){
                        Sanjiao ss2=new Sanjiao(point3,point4,point2);
                        if(ss2.sa.inline(point1)||ss2.sb.inline(point1)||ss2.sc.inline(point1)){
                            System.out.println("on the triangle");
                            return;
                        }
                        else if(ss2.insanjiao(point1)){
                            System.out.println("in the triangle");
                            return;
                        }
                        else{
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                    else if(S.bd.inline(point2)){
                        Sanjiao ss3=new Sanjiao(point4,point5,point3);
                        if(ss3.sa.inline(point1)||ss3.sb.inline(point1)||ss3.sc.inline(point1)){
                            System.out.println("on the triangle");
                            return;
                        }
                        else if(ss3.insanjiao(point1)){
                            System.out.println("in the triangle");
                            return;
                        }
                        else{
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                    else if(S.bd.inline(point4)){
                        Sanjiao ss4=new Sanjiao(point2,point3,point5);
                        if(ss4.sa.inline(point1)||ss4.sb.inline(point1)||ss4.sc.inline(point1)){
                            System.out.println("on the triangle");
                            return;
                        }
                        else if(ss4.insanjiao(point1)){
                            System.out.println("in the triangle");
                            return;
                        }
                        else{
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                }
                System.out.println("not a quadrilateral or triangle");
                break;
            }

        }

    }
    public static boolean geshi(String s){

        String s2= s.substring(0,2);
        if(!s2.matches("[1-5]\\:"))
        {
            System.out.println("Wrong Format");
            return false;
        }
        String s3 = s.substring(2);
        if(!s3.matches("([+|-]?(0|[1-9][0-9]*)(\\.\\d+)?,[+|-]?(0|[1-9][0-9]*)(\\.\\d+)?\\ ?)+"))
        {
            System.out.println("Wrong Format");
            return false;
        }
        return  true;
    }
    public static boolean dianshu(String s){
        String[] a = s.split(":");
        String[] b = a[1].split(" ");
        int n = b.length;
        if (s.charAt(0) == '1' && n != 4) {
            System.out.println("wrong number of points");
            return false;
        } else if (s.charAt(0) == '2' && n != 4) {
            System.out.println("wrong number of points");
            return false;
        } else if (s.charAt(0) == '3' && n != 4) {
            System.out.println("wrong number of points");
            return false;
        } else if (s.charAt(0) == '4' && n != 6) {
            System.out.println("wrong number of points");
            return false;
        } else if (s.charAt(0) == '5' && n != 5) {
            System.out.println("wrong number of points");
            return false;
        }
        return  true;
    }

    static class Point {
        double x,y;
        public void input(double a,double b){
            this.x=a;
            this.y=b;
        }
        public double getx(){
            return x;
        }
        public double gety(){
            return y;
        }
        public double juli(Point p){
            return Math.sqrt((this.x-p.x )*(this.x-p.x )+(this.y-p.y )*(this.y-p.y));
        }
        public double xilv(Point p){

            return (this.y-p.y)/(this.x-p.x);
        }
    }


    static class Line {
        Point x,y;

        Line (Point a, Point b){
            this.x=a;
            this.y=b;

        }
        double length(){
            return this.x.juli(this.y);
        }
        double distance(Point p){//!!!
            if(this.x.x==this.y.x){
                return  (p.x-this.x.x);

            }
            else{
                double e=(this.x.y-this.y.y)/(this.x.x-this.y.x);
                double b=this.x.y-(e*this.x.x);
                return (e*p.x-p.y+b)/Math.sqrt(e*e+1);
            }
        }
        public static boolean intersect(double l1x1,double l1y1,double l1x2,double l1y2,double l2x1,double l2y1,double l2x2,double l2y2) {

            // 快速排斥实验 首先判断两条线段在 x 以及 y 坐标的投影是否有重合。 有一个为真，则代表两线段必不可交。
            if (Math.max(l1x1,l1x2) < Math.min(l2x1 ,l2x2)
                    || Math.max(l1y1,l1y2) < Math.min(l2y1,l2y2)
                    || Math.max(l2x1,l2x2) < Math.min(l1x1,l1x2)
                    || Math.max(l2y1,l2y2) < Math.min(l1y1,l1y2))
            {
                return false;
            }
            // 跨立实验  如果相交则矢量叉积异号或为零，大于零则不相交
            else if ((((l1x1 - l2x1) * (l2y2 - l2y1) - (l1y1 - l2y1) * (l2x2 - l2x1))
                    * ((l1x2 - l2x1) * (l2y2 - l2y1) - (l1y2 - l2y1) * (l2x2 - l2x1))) > 0
                    || (((l2x1 - l1x1) * (l1y2 - l1y1) - (l2y1 - l1y1) * (l1x2 - l1x1))
                    * ((l2x2 - l1x1) * (l1y2 - l1y1) - (l2y2 - l1y1) * (l1x2 - l1x1))) > 0)
            {
                return false;
            }
            return true;
        }
        public double duijiaoxian() {
            double duijiaoxian=Math.sqrt((this.x.x-this.y.x)*(this.x.x-this.y.x)+(this.x.y-this.y.y)*(this.x.y-this.y.y));
            return duijiaoxian;
        }
        public boolean xianchonghe (Line l){
            return this.pingxing(l)&&l.distance(this.x)==0;
        }
        boolean inline(Point p){
            if(this.x.x==this.y.x&&this.y.x==p.x)
                return true;
            double e=(this.x.y-this.y.y)/(this.x.x-this.y.x);
            double b=this.x.y-(e*this.x.x);
            if((e*p.x-p.y+b)==0)
                return true;
            else
                return false;
        }
        Point jiaodian(Line l){
            Point v=sub(l.y,l.x);
            Point w=sub(this.y,this.x);
            Point p=l.x;
            Point q=this.x;
            Point u=sub(p,q);
            double t=cross(w,u)/cross(v,w);
            Point ans =new Point( );
            ans.x=p.x+v.x*t;ans.y=p.y+v.y*t;
            double y0=ans.y;
            double x0=ans.x;
            if(((x0)>=min(x.x,y.x)&&(x0)<=max(x.x,y.x))&&((y0)>=min(x.y,y.y)&&(y0)<=max(x.y,y.y)))
                return ans;
            return null;

        }
        public static double cross (Point a, Point b){
            return a.x*b.y-a.y*b.x;
        }
        public static Point sub(Point a, Point b){
            Point d=new Point();
            d.x=a.x-b.x;d.y=a.y-b.y;
            return d;
        }
        boolean pingxing  (Line a){
            if((a.x.x==a.y.x )&&(this.x.x==this.y.x))
                return true;
            if((a.x.x==a.y.x)&&(this.x.x!=this.y.x))
                return false;
            if((a.x.x!=a.y.x)&&(this.x.x==this.y.x))
                return false;
            double e=a.x.xilv(a.y);
            double e1=this.x.xilv(this.y);
            if(e==e1)
                return true;
            else return false;
        }

    }
    static class Sibian {
        Point a,b,c,d;
        Line ab,bc,cd,da,ac,bd;
        private boolean judge1=false;//0,2
        private boolean judge2=false;//1,3
        Sibian(Point a, Point b, Point c, Point d){
            this.a=a;this.b=b;this.c=c;this.d=d;
            this.ab=new Line(a,b);
            this.bc=new Line(b,c);
            this.cd=new Line(c,d);
            this.da=new Line(d,a);
            this.ac=new Line(a,c);
            this.bd=new Line(b,d);
        }
        public void sibianxing(){
            if(Math.abs((a.y-c.y)*(a.x-b.x)-(a.y-b.y)*(a.x-c.x))<1e-6||
                    Math.abs((a.y-d.y)*(a.x-b.x)-(a.y-b.y)*(a.x-d.x))<1e-6||
                    Math.abs((a.y-d.y)*(a.x-c.x)-(a.y-c.y)*(a.x-d.x))<1e-6||
                    Math.abs((b.y-d.y)*(b.x-c.x)-(b.y-c.y)*(b.x-d.x))<1e-6)System.out.print("false ");
            else {
                if(!Line.intersect(a.x,a.y,d.x,d.y,b.x,b.y,c.x,c.y)) {
                    System.out.print("true ");
                }
                else System.out.print("false ");
            }
        }
        public void pingxingsibianxing(){
            if(this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length())System.out.print("true");
            else System.out.print("false");
        }
        public boolean nengfougoucheng(){
            if(Math.abs((a.y-c.y)*(a.x-b.x)-(a.y-b.y)*(a.x-c.x))<1e-6||
                    Math.abs((a.y-d.y)*(a.x-b.x)-(a.y-b.y)*(a.x-d.x))<1e-6||
                    Math.abs((a.y-d.y)*(a.x-c.x)-(a.y-c.y)*(a.x-d.x))<1e-6||
                    Math.abs((b.y-d.y)*(b.x-c.x)-(b.y-c.y)*(b.x-d.x))<1e-6) {
                return false;
            }
            else return !Line.intersect(a.x, a.y, d.x, d.y, b.x, b.y, c.x, c.y) && !Line.intersect(a.x, a.y, b.x, b.y, d.x, d.y, c.x, c.y);
        }
        public boolean lingxing(){
            return (this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length());
        }
        public boolean changfangxing(){
            Line l1=new Line(a,c);
            double ac=l1.duijiaoxian();
            Line l2=new Line(b,d);
            double bd=l2.duijiaoxian();
            return (ac==bd&&this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length());
        }
        public boolean zhengfangxing(){
            return (lingxing()&& changfangxing());
        }
        public boolean otupanduan() {
            Line l1=new Line(a,c);
            double distance1=l1.distance(b);
            double distance2=l1.distance(d);
            Line l2=new Line(b,d);
            double distance3=l2.distance(a);
            double distance4= l2.distance(c);
            if(distance1*distance2<0)judge1=true;
            if(distance3*distance4<0)judge2=true;
            if(judge1==true&&judge2==true) {
                return true;
            }
            return false;
        }
        public double zhouchang() {
            double ab=this.ab.length();
            double bc=this.bc.length();
            double cd=this.cd.length();
            double da=this.da.length();
            double c=ab+bc+cd+da;
            double C=outformat(c);
            return C;
        }
        public double area() {
            double area=0;
            double area1=0;
            double area2=0;
            double are=0;
            //凸四边形
            if(judge1==true&&judge2==true) {
                area1=Math.abs((b.x*c.y+c.x*d.y+d.x*b.y-b.x*d.y-c.x*b.y-d.x*c.y)/2);
                area2=Math.abs((b.x*a.y+a.x*d.y+d.x*b.y-b.x*d.y-a.x*b.y-d.x*a.y)/2);
                area=area1+area2;
                are= outformat(area);
            }
            else if(judge1==false) {
                area1=Math.abs((b.x*d.y+d.x*a.y+a.x*b.y-b.x*a.y-d.x*b.y-a.x*d.y)/2);
                area2=Math.abs((d.x*c.y+c.x*b.y+b.x*d.y-d.x*b.y-c.x*d.y-b.x*c.y)/2);
                area=area1+area2;
                are= outformat(area);
            }
            else if(judge2==false) {
                area1=Math.abs((b.x*c.y+c.x*a.y+a.x*b.y-b.x*a.y-c.x*b.y-a.x*c.y)/2);
                area2=Math.abs((d.x*c.y+c.x*a.y+a.x*d.y-d.x*a.y-c.x*d.y-a.x*c.y)/2);
                area=area1+area2;
                are=outformat(area);
            }
            return are;
        }
        public Double outformat(double num) {
            if(num*1e+3%10!=0) {
                String num1=String.format("%.3f",num);
                return Double.valueOf(num1);
            }
            return num;
        }
        public boolean bianchonghe (Line l){
            if(this.ab.xianchonghe(l)){
                return true;
            }
            else if(this.bc.xianchonghe(l)){
                return true;
            }
            else if(this.cd.xianchonghe(l)){
                return true;
            }
            else if(this.da.xianchonghe(l)){
                return true;
            }
            return false;
        }
        public boolean insibian(Point p){
            double m=0;
            if(otupanduan()){
                m=area();
            }

            Sanjiao ss1=new Sanjiao(p,a,b);
            Sanjiao ss2=new Sanjiao(p,b,c);
            Sanjiao ss3=new Sanjiao(p,c,d);
            Sanjiao ss4=new Sanjiao(p,d,a);
            double m1=ss1.mianji();
            double m2=ss2.mianji();
            double m3=ss3.mianji();
            double m4=ss4.mianji();
            if(Math.abs(m-(m1+m2+m3+m4))<0.1)
                return true;
            else return false;
        }
        public int fengesibainxing(Line l){
            int num=0;
           Point jiaodian1= this.ab.jiaodian(l);
           Point jiaodian2 = this.bc.jiaodian(l);
           Point jiaodian3 = this.cd.jiaodian(l);
           Point jiaodian4 =this.da.jiaodian(l);

           if(jiaodian1==null&&jiaodian2==null&&jiaodian3==null&&jiaodian4==null)
               return num;
           if( this.ab.jiaodian(l)!=null&&  this.bc.jiaodian(l)!=null){
               //System.exit(-1);
               if(jiaodian1.x==jiaodian2.x&&jiaodian1.y==jiaodian2.y)
                   num=1;
               else num=2;
           }
            else if(this.ab.jiaodian(l)!=null&& this.cd.jiaodian(l)!=null){
               //System.exit(-1);
                if(jiaodian1.x==jiaodian3.x&&jiaodian1.y==jiaodian3.y)
                    num=1;
                else num=2;
            }
            else if(this.ab.jiaodian(l)!=null&& this.da.jiaodian(l)!=null){
               //System.exit(-1);
                if(jiaodian1.x==jiaodian4.x&&jiaodian1.y==jiaodian4.y)
                    num=1;
                else num=2;
            }
            if(this.bc.jiaodian(l)!=null&& this.cd.jiaodian(l)!=null){
                //System.exit(-1);
                if(jiaodian2.x==jiaodian3.x&&jiaodian2.y==jiaodian3.y)
                    num=1;
                else num=2;
            }
            if(this.bc.jiaodian(l)!=null&&this.da.jiaodian(l)!=null){
                //System.exit(-1);
                if(jiaodian2.x==jiaodian4.x&&jiaodian2.y==jiaodian4.y)
                    num=1;
                else num=2;
            }
            if(this.cd.jiaodian(l)!=null&& this.da.jiaodian(l)!=null){
                //System.exit(-1);
                if(jiaodian3.x==jiaodian4.x&&jiaodian3.y==jiaodian4.y)
                    num=1;
                else num=2;
            }
           return num;
        }
    }

    static class Sanjiao {
        Point sx,sy,sz;
        Line sa,sb,sc;
        Sanjiao (Point a, Point b, Point c){
            this.sx=a;
            this.sy=b;
            this.sz=c;
            this.sa=new Line(b,c);
            this.sb=new Line(a,c);
            this.sc=new Line(a,b);
        }
        public boolean gouchengsanjiao(){
            if(((this.sa.length()+this.sb.length())<=this.sc.length())||((this.sa.length()+this.sc.length())<=this.sb.length())||((this.sb.length()+this.sc.length())<=this.sa.length())){
                return true;
            }
            else return false;
        }

        public double zhouchang(){
            return (this.sa.length()+this.sb.length()+this.sc.length());
        }
        public double mianji(){
            double area=0;
            double s=(this.sa.length()+this.sb.length()+this.sc.length())/2;
            return area=Math.sqrt(s*(s-this.sa.length())*(s-this.sb.length())*(s-this.sc.length()));
        }
        public int type(){
            double[] num = new double[3];
            num[0] = this.sa.length();num[1] = this.sb.length();num[2] = this.sc.length();
            Arrays.sort(num);
            double tmp = Math.pow(num[0],2) + Math.pow(num[1],2) - Math.pow(num[2],2);
            if(Math.abs(tmp) < 0.0000001) return 1;
            if(tmp < 0) return 2;
            return 0;
        }
        public boolean insanjiao(Point p){
            Sanjiao san1=new Sanjiao(p,sx,sy);
            Sanjiao san2=new Sanjiao(p,sy,sz);
            Sanjiao san3=new Sanjiao(p,sz,sx);
            double m1=san1.mianji();
            double m2=san2.mianji();
            double m3=san3.mianji();
            if(Math.abs(this.mianji()-(m1+m2+m3))<0.1)
                return true;
            else return false;
        }

    }

}

View Code

圈复杂度分析：

 

 

 

优缺点：

优点：1.对每个方法的计算严谨，尽量减少了存在的误差。

2.使用了面向过程，创建多个类，进行协同完成，减少了代码冗余。

缺点：1.在构造点和线且赋值的时候繁琐，容易出现混乱。

2.由于时间和水平的有限，没能完成全部的选项。

3.没有用到继承和重载的方法，代码冗余还是有些多。

7-3 设计一个银行业务类

编写一个银行业务类BankBusiness，具有以下属性和方法：
（1）公有、静态的属性：银行名称bankName，初始值为“中国银行”。
（2）私有属性：账户名name、密码password、账户余额balance。
（3）银行对用户到来的欢迎（welcome）动作（静态、公有方法），显示“中国银行欢迎您的到来！”，其中“中国银行”自动使用bankName的值。
（4）银行对用户离开的提醒（welcomeNext）动作（静态、公有方法），显示“请收好您的证件和物品，欢迎您下次光临！”
（5）带参数的构造方法，完成开户操作。需要账户名name、密码password信息，同时让账户余额为0。
（6）用户的存款（deposit）操作（公有方法，需要密码和交易额信息），密码不对时无法存款且提示“您的密码错误！”；密码正确、完成用户存款操作后，要提示用户的账户余额，例如“您的余额有1000.0元。”。
（7）用户的取款（withdraw）操作（公有方法，需要密码和交易额信息）。密码不对时无法取款且提示“您的密码错误！”；密码正确但余额不足时提示“您的余额不足！”；密码正确且余额充足时扣除交易额并提示用户的账户余额，例如“请取走钞票，您的余额还有500.0元。”。

编写一个测试类Main，在main方法中，先后执行以下操作：
（1）调用BankBusiness类的welcome()方法。
（2）接收键盘输入的用户名、密码信息作为参数，调用BankBusiness类带参数的构造方法，从而创建一个BankBusiness类的对象account。
（3）调用account的存款方法，输入正确的密码，存入若干元。密码及存款金额从键盘输入。
（4）调用account的取款方法，输入错误的密码，试图取款若干元。密码及取款金额从键盘输入。
（5）调用account的取款方法，输入正确的密码，试图取款若干元（取款金额大于余额）。密码及取款金额从键盘输入。
（6）调用account的取款方法，输入正确的密码，试图取款若干元（取款金额小于余额）。密码及取款金额从键盘输入。
（7）调用BankBusiness类的welcomeNext()方法。

输入格式:

输入开户需要的姓名、密码
输入正确密码、存款金额
输入错误密码、取款金额
输入正确密码、大于余额的取款金额
输入正确密码、小于余额的取款金额

输出格式:

中国银行（银行名称）欢迎您的到来！
您的余额有多少元。
您的密码错误！
您的余额不足！
请取走钞票，您的余额还有多少元。
请收好您的证件和物品，欢迎您下次光临！

代码思路：这次题目比较简单，题目中也是说出了要建的类，而且里面的相关方法也清楚，按照题目给的直接写就可以，主要是逐行接受信息。

主要代码：

import java.util.Scanner;
public class Main{
    public static void main(String[] args) {
        Scanner str=new Scanner(System.in);
        BankBusiness account=new BankBusiness();
        String s=str.nextLine();
        String name,password;
        Double balance=0.0;
        account.welcome();
        String []a=s.split(" ");
        name=a[0];
        password=a[1];
        account.kaihu(name,password);
        s=str.nextLine();
        String []b=s.split(" ");
        password=b[0];
        balance= Double.valueOf(b[1]);
        account.deposit(password,balance);
        for(int i=0;i<3;i++){
            s=str.nextLine();
            String []c=s.split(" ");
            password=c[0];
            balance= Double.valueOf(c[1]);
            account.withdraw(password,balance);
        }
        account.welcomeNext();
    }
    static class BankBusiness {
        public static String bankName="中国银行";
        private String name,password;
        private Double balance;
        public  void welcome(){
            System.out.println(bankName+"欢迎您的到来！");
        }
        public  void welcomeNext(){
            System.out.println("请收好您的证件和物品，欢迎您下次光临！");
        }
        public void kaihu(String name,String password){
            this.name=name;
            this.password=password;
            this.balance=0.0;
        }
        public void deposit(String password,Double money){
            if(!this.password.equals(password)){//!!!字符串不能这么比较啊o
                System.out.println("您的密码错误！");
                System.exit(0);
            }
            else{
                this.balance+=money;
            }
            System.out.println("您的余额有"+this.balance+"元。");
        }
        public void withdraw(String password,Double money){
            if(!this.password.equals(password)){//!!!字符串不能这么比较啊o
                System.out.println("您的密码错误！");
                return ;
                // System.exit(0);使用时会退出整个程序，后面的都不会在执行
            }
            else if(this.balance<money){
                System.out.println("您的余额不足！");
            }
            else{
                this.balance-=money;
                System.out.println("请取走钞票，您的余额还有"+this.balance+"元。");
            }
        }

    }

}

View Code

题目集五：

7-1 点线形系列5-凸五边形的计算

用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入五个点坐标，判断是否是五边形，判断结果输出true/false。
2：输入五个点坐标，判断是凹五边形（false）还是凸五边形(true)，如果是凸五边形，则再输出五边形周长、面积，结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形，输出"not a pentagon"
3：输入七个点坐标，前两个点构成一条直线，后五个点构成一个凸五边形、凸四边形或凸三角形，输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个，再按面积从小到大输出被直线分割成两部分的面积（不换行）。若直线与多边形形的一条边线重合，输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入，若前两点重合，输出"points coincide"。

以上3选项中，若输入的点无法构成多边形，则输出"not a polygon"。输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

4：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），判断它们两个之间是否存在包含关系（一个多边形有一条或多条边与另一个多边形重合，其他部分都包含在另一个多边形内部，也算包含）。
两者存在六种关系：1、分离（完全无重合点） 2、连接（只有一个点或一条边重合） 3、完全重合 4、被包含（前一个多边形在后一个多边形的内部）5、交错 6、包含（后一个多边形在前一个多边形的内部）。
各种关系的输出格式如下：
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon

5：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），输出两个多边形公共区域的面积。注：只考虑每个多边形被另一个多边形分割成最多两个部分的情况，不考虑一个多边形将另一个分割成超过两个区域的情况。
6：输入六个点坐标，输出第一个是否在后五个点所构成的多边形（限定为凸多边形，不考虑凹多边形），的内部（若是五边形输出in the pentagon/outof the pentagon，若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。输入入错存在冗余点要排除，冗余点的判定方法见选项5。如果点在多边形的某条边上，输出"on the triangle/on the quadrilateral/on the pentagon"。
以上4、5、6选项输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

输入格式:

基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

输出格式:

基本输出格式见每种选项的描述。
异常情况输出：
如果不符合基本格式，输出"Wrong Format"。
如果符合基本格式，但输入点的数量不符合要求，输出"wrong number of points"。
注意：输出的数据若小数点后超过3位，只保留小数点后3位，多余部分采用四舍五入规则进到最低位。小数点后若不足3位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333，1.0按格式输出为1.0

代码思路：首先还是进行各种类的创建，其他的类都和第四次大作业的四边形一样，这次主要增加五边形类和主类，然后根据题目的要求调用各个类的方法等进行解答。

五边形类：

public class Wubianxing {
        Point a,b,c,d,e;
        Line ab,bc,cd,de,ea,ac,ad,bd,be,ce;
        Wubianxing(Point a,Point b,Point c,Point d,Point e){
            this.a=a;this.b=b;this.c=c;this.d=d;this.e=e;
            this.ab=new Line(a,b);this.bc=new Line(b,c);this.cd=new Line(c,d);this.de=new Line(d,e);
            this.ea=new Line(e,a);this.ac=new Line(a,c);this.ad=new Line(a,d);this.bd=new Line(b,d);
            this.be=new Line(b,e);this.ce=new Line(c,e);
        }
        public boolean iswubianxing(){
            if(ab.pingxing(bc)||bc.pingxing(cd)||cd.pingxing(de)||de.pingxing(ea)){
                return false;
            }
            else if(Line.intersect(a.x,a.y,b.x,b.y,c.x,c.y,d.x,d.y)||Line.intersect(a.x,a.y,b.x,b.y,d.x,d.y,e.x,e.y)||
                    Line.intersect(b.x,b.y,c.x,c.y,d.x,d.y,e.x,e.y)||Line.intersect(b.x,b.y,c.x,c.y,e.x,e.y,a.x,a.y)||
                    Line.intersect(c.x,c.y,d.x,d.y,e.x,e.y,a.x,a.y))
                return false;

            return true;
        }
        public boolean istuwubianxing(){
            if((((b.x-a.x)*(c.y-b.y))-((c.x-b.x)*(b.y-a.y))>0&&((c.x-b.x)*(d.y-c.y))-((d.x-c.x)*(c.y-b.y))>0&&
                    ((d.x-c.x)*(e.y-d.y))-((e.x-d.x)*(d.y-c.y))>0&&((e.x-d.x)*(a.y-e.y))-((a.x-e.x)*(e.y-d.y))>0)||
                    (((b.x-a.x)*(c.y-b.y))-((c.x-b.x)*(b.y-a.y))<0&&((c.x-b.x)*(d.y-c.y))-((d.x-c.x)*(c.y-b.y))<0&&
                            ((d.x-c.x)*(e.y-d.y))-((e.x-d.x)*(d.y-c.y))<0&&((e.x-d.x)*(a.y-e.y))-((a.x-e.x)*(e.y-d.y))<0))
                return true;
            else
                return false;
        }
        public double zhouchang(){
            double c=this.ab.length()+this.bc.length()+this.cd.length()+this.de.length()+this.ea.length();
            double C=outformat(c);
            return  C;
        }
        public double area(){
            Sanjiao san1=new Sanjiao(this.a,this.b,this.c);Sanjiao san2=new Sanjiao(this.a,this.c,this.d);
            Sanjiao san3=new Sanjiao(this.a,this.d,this.e);
            double mj= san1.mianji()+ san2.mianji()+ san3.mianji();
            double mianji=outformat(mj);
            return mianji;
        }
        public Double outformat(double num) {
            if(num*1e+3%10!=0) {
                String num1=String.format("%.3f",num);
                return Double.valueOf(num1);
            }
            return num;
        }
        public boolean bianchonghe (Line l){
            if(this.ab.xianchonghe(l)){
                return true;
            }
            else if(this.bc.xianchonghe(l)){
                return true;
            }
            else if(this.cd.xianchonghe(l)){
                return true;
            }
            else if(this.de.xianchonghe(l)){
                return true;
            }
            else if(this.ea.xianchonghe(l)){
                return true;
            }
            return false;
        }
        public void fengewubainxing(Line l) {
            double area1=0,area2=0;

            if(this.ac.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.a,this.b,this.c);
                area1=ss1.mianji();
                area2=this.area()-area1;
                out(area1,area2);
            }
            else if(this.ad.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.a,this.d,this.e);
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.bd.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.b,this.d,this.c);
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.be.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.a,this.b,this.e);
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ce.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.c,this.d,this.e);
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ab.jiaodian(l)!=null&&this.bc.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.bc.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.ab.jiaodian(l),this.b,this.bc.jiaodian(l));
                area1= ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ab.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.ab.jiaodian(l),this.b,this.c,this.cd.jiaodian(l));
                ss1.otupanduan();
                area1= ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ab.jiaodian(l)!=null&&this.de.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.a,this.ab.jiaodian(l),this.de.jiaodian(l),this.e);
                ss1.otupanduan();
                area1= ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ab.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.ea.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.ab.jiaodian(l),this.a,this.ea.jiaodian(l));
                area1= ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.bc.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null&&this.bc.jiaodian(l)!=this.cd.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.bc.jiaodian(l),this.c,this.cd.jiaodian(l));
                area1= ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.bc.jiaodian(l)!=null&&this.de.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.bc.jiaodian(l),this.c,this.d,this.de.jiaodian(l));
                ss1.otupanduan();
                area1= ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.bc.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.bc.jiaodian(l),this.ea.jiaodian(l),this.a,this.b);
                ss1.otupanduan();
                area1= ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.cd.jiaodian(l)!=null&&this.de.jiaodian(l)!=null&&this.cd.jiaodian(l)!=this.de.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.cd.jiaodian(l),this.d,this.de.jiaodian(l));
                area1= ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.cd.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.cd.jiaodian(l),this.ea.jiaodian(l),this.e,this.d);
                ss1.otupanduan();
                area1= ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.de.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null&&this.ea.jiaodian(l)!=this.de.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.ea.jiaodian(l),this.e,this.de.jiaodian(l));
                area1= ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else {
                System.out.println(0);
                System.exit(0);
            }
        }
        public void out(double m1,double m2){
            if(m1>=m2){
                System.out.println(2+" "+m2+" "+m1);
                System.exit(0);
            }
            else{
                System.out.println(2+" "+m1+" "+m2);
                System.exit(0);
            }
        }
        public boolean inwubianxing(Point p){
            Sanjiao ss1=new Sanjiao(this.a,this.b,p);Sanjiao ss2=new Sanjiao(this.b,this.c,p);
            Sanjiao ss3=new Sanjiao(this.c,this.d,p);Sanjiao ss4=new Sanjiao(this.d,this.e,p);
            Sanjiao ss5=new Sanjiao(this.e,this.a,p);
            if(Math.abs(this.area()-(ss1.mianji()+ss2.mianji()+ss3.mianji()+ss4.mianji()+ss5.mianji()))<0.0001)
                return true;
           else  return false;
        }
    }

View Code

圈复杂度分析：

主要代码：

import java.util.Arrays;
import java.util.Scanner;

import static java.lang.Math.max;
import static java.lang.Math.min;

public class Main {
    public static void main(String[] args) {
        Scanner str=new Scanner(System.in);
        String s=str.nextLine();
        if (!geshi(s)) return;
        if (!dianshu(s)) return;
        String s1=s.substring(2);
        String []b=s1.split(",| ");
        int choice = s.charAt(0)-48;
        switch (choice){
            case 1: {
                double x1 = Double.parseDouble(b[0]);double y1 = Double.parseDouble(b[1]);
                double x2 = Double.parseDouble(b[2]);double y2 = Double.parseDouble(b[3]);
                double x3 = Double.parseDouble(b[4]);double y3 = Double.parseDouble(b[5]);
                double x4 = Double.parseDouble(b[6]);double y4 = Double.parseDouble(b[7]);
                double x5 = Double.parseDouble(b[8]);double y5 = Double.parseDouble(b[9]);

                Point point1 = new Point(x1,y1);Point point2 = new Point(x2,y2);Point point3 = new Point(x3,y3);
                Point point4 = new Point(x4,y4);Point point5 = new Point(x5,y5);

                Wubianxing W = new Wubianxing(point1, point2, point3, point4, point5);
                if (W.iswubianxing()) System.out.println("true");
                else System.out.println("false");
                break;
            }
            case 2:{
                double x1 = Double.parseDouble(b[0]);double y1 = Double.parseDouble(b[1]);
                double x2 = Double.parseDouble(b[2]);double y2 = Double.parseDouble(b[3]);
                double x3 = Double.parseDouble(b[4]);double y3 = Double.parseDouble(b[5]);
                double x4 = Double.parseDouble(b[6]);double y4 = Double.parseDouble(b[7]);
                double x5 = Double.parseDouble(b[8]);double y5 = Double.parseDouble(b[9]);

                Point point1 = new Point(x1,y1);Point point2 = new Point(x2,y2);
                Point point3 = new Point(x3,y3);Point point4 = new Point(x4,y4);
                Point point5 = new Point(x5,y5);

                Wubianxing W = new Wubianxing(point1, point2, point3, point4, point5);
                if(W.iswubianxing()) {
                    if (W.istuwubianxing()) {System.out.print("true");
                        System.out.print(" "+W.zhouchang()+" "+W.area());
                    }
                    else System.out.print("false");
                }

                else System.out.println("not a pentagon");
                break;
            }
            case 3:{
                double x1 = Double.parseDouble(b[0]);double y1 = Double.parseDouble(b[1]);
                double x2 = Double.parseDouble(b[2]);double y2 = Double.parseDouble(b[3]);
                double x3 = Double.parseDouble(b[4]);double y3 = Double.parseDouble(b[5]);
                double x4 = Double.parseDouble(b[6]);double y4 = Double.parseDouble(b[7]);
                double x5 = Double.parseDouble(b[8]);double y5 = Double.parseDouble(b[9]);
                double x6 = Double.parseDouble(b[10]);double y6 = Double.parseDouble(b[11]);
                double x7 = Double.parseDouble(b[12]);double y7 = Double.parseDouble(b[13]);

                Point point1 = new Point(x1,y1);Point point2 = new Point(x2,y2);
                Point point3 = new Point(x3,y3);Point point4 = new Point(x4,y4);
                Point point5 = new Point(x5,y5);Point point6 = new Point(x6,y6);
                Point point7 = new Point(x7,y7);

                if ((x1==x2&&y1==y2)) {
                    System.out.println("points coincide");
                    return;
                }
                Line l=new Line(point1,point2);
                Wubianxing W=new Wubianxing(point3,point4,point5,point6,point7);
                if(W.iswubianxing()){
                    if(W.bianchonghe(l)){
                        System.out.println("The line is coincide with one of the lines");
                        return;
                    }
                    W.fengewubainxing(l);
                }
                Sibian si1=new Sibian(point3,point5,point6,point7);
                 if(W.ac.inline(point4)&&si1.nengfougoucheng()){
                        if(si1.bianchonghe(l)){
                            System.out.println("The line is coincide with one of the lines");
                            return;
                        }
                        si1.fengesibianxing(l);
                }
                 Sibian si2=new Sibian(point3,point4,point5,point6);
                 if(W.ad.inline(point7)&&si2.nengfougoucheng()){
                        if(si2.bianchonghe(l)){
                            System.out.println("The line is coincide with one of the lines");
                            return;
                        }
                        si2.fengesibianxing(l);
                }
                 Sibian si3=new Sibian(point3,point4,point6,point7);
                 if(W.bd.inline(point5)&&si3.nengfougoucheng()){

                        if(si3.bianchonghe(l)){
                            System.out.println("The line is coincide with one of the lines");
                            return;
                        }
                        si3.fengesibianxing(l);
                }Sibian si4=new Sibian(point4,point5,point6,point7);
                if(W.be.inline(point3)&&si4.nengfougoucheng()){
                        if(si4.bianchonghe(l)){
                            System.out.println("The line is coincide with one of the lines");
                            return;
                        }
                        si4.fengesibianxing(l);
                }
                Sibian si5=new Sibian(point3,point4,point5,point7);
                 if(W.ce.inline(point6)&&si5.nengfougoucheng()){
                        if(si5.bianchonghe(l)){
                            System.out.println("The line is coincide with one of the lines");
                            return;
                        }
                        si5.fengesibianxing(l);
                }
                else if (W.ac.inline(point7)&&W.ac.inline(point6)) {
                    Sanjiao san=new Sanjiao(point3,point4,point5);
                    if(san.gouchengsanjiao()){
                        san.fengesanjiaoxing(l);
                    }
                }
                else if (W.ad.inline(point4)&&W.ad.inline(point5)) {
                    Sanjiao san=new Sanjiao(point3,point6,point7);
                    if(san.gouchengsanjiao()){
                        san.fengesanjiaoxing(l);
                    }
                }
                else if (W.bd.inline(point7)&&W.bd.inline(point3)) {
                    Sanjiao san=new Sanjiao(point6,point4,point5);
                    if(san.gouchengsanjiao()){
                        san.fengesanjiaoxing(l);
                    }
                }
                else if (W.be.inline(point5)&&W.be.inline(point6)) {
                    Sanjiao san=new Sanjiao(point3,point4,point7);
                    if(san.gouchengsanjiao()){
                        san.fengesanjiaoxing(l);
                    }
                }
                else if (W.ce.inline(point3)&&W.ce.inline(point4)) {
                    Sanjiao san=new Sanjiao(point5,point6,point7);
                    if(san.gouchengsanjiao()){
                        san.fengesanjiaoxing(l);
                    }
                }
                else if (W.ac.inline(point4)&&W.ad.inline(point7)) {
                    Sanjiao san=new Sanjiao(point3,point6,point5);
                    if(san.gouchengsanjiao()){
                        san.fengesanjiaoxing(l);
                    }
                }
                else if (W.bd.inline(point5)&&W.be.inline(point3)) {
                    Sanjiao san=new Sanjiao(point4,point6,point7);
                    if(san.gouchengsanjiao()){
                        san.fengesanjiaoxing(l);
                    }
                }
                else if (W.ac.inline(point4)&&W.ce.inline(point6)) {
                    Sanjiao san=new Sanjiao(point3,point7,point5);
                    if(san.gouchengsanjiao()){
                        san.fengesanjiaoxing(l);
                    }
                }
                else if (W.bd.inline(point5)&&W.ad.inline(point7)) {
                    Sanjiao san=new Sanjiao(point3,point4,point6);
                    if(san.gouchengsanjiao()){
                        san.fengesanjiaoxing(l);
                    }
                }
                else if (W.be.inline(point3)&&W.ce.inline(point6)) {
                    Sanjiao san=new Sanjiao(point7,point4,point5);
                    if(san.gouchengsanjiao()){
                        san.fengesanjiaoxing(l);
                    }
                }
                break;
            }
            case 4:{
                double x1 = Double.parseDouble(b[0]);double y1 = Double.parseDouble(b[1]);
                double x2 = Double.parseDouble(b[2]);double y2 = Double.parseDouble(b[3]);
                double x3 = Double.parseDouble(b[4]);double y3 = Double.parseDouble(b[5]);
                double x4 = Double.parseDouble(b[6]);double y4 = Double.parseDouble(b[7]);
                double x5 = Double.parseDouble(b[8]);double y5 = Double.parseDouble(b[9]);
                double x6 = Double.parseDouble(b[10]);double y6 = Double.parseDouble(b[11]);
                double x7 = Double.parseDouble(b[12]);double y7 = Double.parseDouble(b[13]);
                double x8 = Double.parseDouble(b[14]);double y8 = Double.parseDouble(b[15]);
                double x9 = Double.parseDouble(b[16]);double y9 = Double.parseDouble(b[17]);
                double x10 = Double.parseDouble(b[18]);double y10 = Double.parseDouble(b[19]);
                Point point1 = new Point(x1,y1);Point point2 = new Point(x2,y2); Point point7 = new Point(x7,y7);Point point8 = new Point(x8,y8);
                Point point3 = new Point(x3,y3);Point point4 = new Point(x4,y4); Point point9 = new Point(x9,y9);Point point10 = new Point(x10,y10);
                Point point5 = new Point(x5,y5);Point point6 = new Point(x6,y6);
                Wubianxing wu1=new Wubianxing(point1,point2,point3,point4,point5);Wubianxing wu2=new Wubianxing(point6,point7,point8,point9,point10);
                if(wu1.iswubianxing()&&wu2.iswubianxing()){
                    if((x1==x6&&y1==y6&&x2==x7&&y2==y7&&x3==x8&&y3==y8&&x4==x9&&y4==y9&&x5==x10&&y5==y10)){
                        System.out.println("the previous pentagon coincides with the following pentagon");
                        return;
                    }
                    else {
                        System.out.println("the previous pentagon is connected to the following pentagon");
                        return;
                    }
                }
                Sibian si1=new Sibian(point1,point3,point4,point5);
                if(wu1.ac.inline(point3)&&si1.nengfougoucheng()&&wu2.iswubianxing()){
                    if(si1.insibian(wu2.a)&&si1.insibian(wu2.b)&&si1.insibian(wu2.c)&&si1.insibian(wu2.d)&&si1.insibian(wu2.e)){
                        System.out.println("the previous quadrilateral contains the following pentagon");
                        return;
                    }
                    else if(wu2.inwubianxing(si1.a)&&wu2.inwubianxing(si1.b)&&wu2.inwubianxing(si1.c)&&wu2.inwubianxing(si1.d)){
                        System.out.println("the previous quadrilateral is inside the following pentagon");
                        return;
                    }
                    else if(x1==x6&&y1==y6){
                        System.out.println("the previous quadrilateral is connected to the following pentagon");
                        return;
                    }
                    else {
                        System.out.println("the previous quadrilateral is interlaced with the following pentagon");
                        return;
                    }
                }
                if(wu1.iswubianxing()&&(wu2.ac.inline(point9)&&wu2.ac.inline(point10))){
                    Sanjiao san = new Sanjiao(point6, point7, point8);
                    System.out.println("the previous pentagon is interlaced with the following triangle");
                    return;
                }
                if (wu1.ac.inline(point2)&&wu1.ce.inline(point4)&&wu2.ac.inline(point7)&&wu2.ce.inline(point9)) {
                    Sanjiao san1 = new Sanjiao(point1, point3, point5);Sanjiao san2 = new Sanjiao(point6, point8, point10);
                    System.out.println("the previous triangle is interlaced with the following triangle");
                    return;
                }
                if (wu1.ac.inline(point2)&&wu1.ce.inline(point4)&&wu2.ad.inline(point7)&&wu2.ad.inline(point8)) {
                    Sanjiao san1 = new Sanjiao(point1, point3, point5);Sanjiao san2 = new Sanjiao(point6, point9, point10);
                    System.out.println("the previous triangle is interlaced with the following triangle");
                    return;
                }
                //、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
                else System.out.println("the previous quadrilateral coincides with the following quadrilateral");
                break;
            }
            case 5:{
                double x1 = Double.parseDouble(b[0]);double y1 = Double.parseDouble(b[1]);
                double x2 = Double.parseDouble(b[2]);double y2 = Double.parseDouble(b[3]);
                double x3 = Double.parseDouble(b[4]);double y3 = Double.parseDouble(b[5]);
                double x4 = Double.parseDouble(b[6]);double y4 = Double.parseDouble(b[7]);
                double x5 = Double.parseDouble(b[8]);double y5 = Double.parseDouble(b[9]);
                double x6 = Double.parseDouble(b[10]);double y6 = Double.parseDouble(b[11]);
                double x7 = Double.parseDouble(b[12]);double y7 = Double.parseDouble(b[13]);
                double x8 = Double.parseDouble(b[14]);double y8 = Double.parseDouble(b[15]);
                double x9 = Double.parseDouble(b[16]);double y9 = Double.parseDouble(b[17]);
                double x10 = Double.parseDouble(b[18]);double y10 = Double.parseDouble(b[19]);
                Point point1 = new Point(x1,y1);Point point2 = new Point(x2,y2); Point point7 = new Point(x7,y7);Point point8 = new Point(x8,y8);
                Point point3 = new Point(x3,y3);Point point4 = new Point(x4,y4); Point point9 = new Point(x9,y9);Point point10 = new Point(x10,y10);
                Point point5 = new Point(x5,y5);Point point6 = new Point(x6,y6);
                Wubianxing wu1=new Wubianxing(point1,point2,point3,point4,point5);Wubianxing wu2=new Wubianxing(point6,point7,point8,point9,point10);
                if(wu1.iswubianxing()&&wu2.iswubianxing()){
                    if((x1==x6&&y1==y6&&x2==x7&&y2==y7&&x3==x8&&y3==y8&&x4==x9&&y4==y9&&x5==x10&&y5==y10)){
                        System.out.println(wu1.area());
                        return;
                    }
                }
                Sibian si1=new Sibian(point1,point3,point4,point5);Sibian si2=new Sibian(point6,point8,point9,point10);
                if(wu1.ac.inline(point3)&&si1.nengfougoucheng()&&wu2.ac.inline(point7)){
                    if((x1==x6&&y1==y6&&x3==x8&&y3==y8&&x4==x9&&y4==y9&&x5==x10&&y5==y10)){
                        System.out.println(si1.area());
                        return;
                    }
                    else if(si2.insibian(si1.a)&&si2.insibian(si1.b)&&si2.insibian(si1.c)&&si2.insibian(si1.d)){
                        System.out.println(si1.area());
                        return;
                    }
                }
            }
            case 6:{
                double x1 = Double.parseDouble(b[0]);double y1 = Double.parseDouble(b[1]);
                double x2 = Double.parseDouble(b[2]);double y2 = Double.parseDouble(b[3]);
                double x3 = Double.parseDouble(b[4]);double y3 = Double.parseDouble(b[5]);
                double x4 = Double.parseDouble(b[6]);double y4 = Double.parseDouble(b[7]);
                double x5 = Double.parseDouble(b[8]);double y5 = Double.parseDouble(b[9]);
                double x6 = Double.parseDouble(b[10]);double y6 = Double.parseDouble(b[11]);
                Point point1 = new Point(x1,y1);Point point2 = new Point(x2,y2);
                Point point3 = new Point(x3,y3);Point point4 = new Point(x4,y4);
                Point point5 = new Point(x5,y5);Point point6 = new Point(x6,y6);
                Wubianxing wu=new Wubianxing(point2,point3,point4,point5,point6);
                if(wu.iswubianxing()){
                    if(wu.ab.inline(point1)||wu.bc.inline(point1)||wu.cd.inline(point1)||wu.de.inline(point1)||wu.ea.inline(point1)){
                        System.out.println("on the pentagon");
                        return;
                    }
                   if(wu.inwubianxing(point1)) {
                       System.out.println("in the pentagon");
                       return;
                   }
                   else{
                       System.out.println("outof the pentagon");
                       return;
                   }
                }
                Sibian si1=new Sibian(point2,point4,point5,point6);
                if(wu.ac.inline(point3)&&si1.nengfougoucheng()){
                    if(si1.ab.inline(point1)||si1.bc.inline(point1)||si1.cd.inline(point1)||si1.da.inline(point1)){
                        System.out.println("on the quadrilateral");
                        return;
                    }
                    if(si1.insibian(point1)) {
                        System.out.println("in the quadrilateral");
                        return;
                    }
                    else{
                        System.out.println("outof the quadrilateral");
                        return;
                    }
                }
                Sibian si2=new Sibian(point3,point4,point5,point2);
                if(wu.ad.inline(point6)&&si2.nengfougoucheng()){
                    if(si2.ab.inline(point1)||si2.bc.inline(point1)||si2.cd.inline(point1)||si2.da.inline(point1)){
                        System.out.println("on the quadrilateral");
                        return;
                    }
                    if(si2.insibian(point1)) {
                        System.out.println("in the quadrilateral");
                        return;
                    }
                    else{
                        System.out.println("outof the quadrilateral");
                        return;
                    }
                }
                Sibian si3=new Sibian(point2,point3,point5,point6);
                if(wu.bd.inline(point4)&&si3.nengfougoucheng()){
                    if(si3.ab.inline(point1)||si3.bc.inline(point1)||si3.cd.inline(point1)||si3.da.inline(point1)){
                        System.out.println("on the quadrilateral");
                        return;
                    }
                    if(si3.insibian(point1)) {
                        System.out.println("in the quadrilateral");
                        return;
                    }
                    else{
                        System.out.println("outof the quadrilateral");
                        return;
                    }
                }Sibian si4=new Sibian(point4,point5,point6,point3);
                if(wu.be.inline(point2)&&si4.nengfougoucheng()){
                    if(si4.ab.inline(point1)||si4.bc.inline(point1)||si4.cd.inline(point1)||si4.da.inline(point1)){
                        System.out.println("on the quadrilateral");
                        return;
                    }
                    if(si4.insibian(point1)) {
                        System.out.println("in the quadrilateral");
                        return;
                    }
                    else{
                        System.out.println("outof the quadrilateral");
                        return;
                    }
                }
                Sibian si5=new Sibian(point2,point3,point4,point6);
                if(wu.ce.inline(point5)&&si5.nengfougoucheng()){
                    if(si5.ab.inline(point1)||si5.bc.inline(point1)||si5.cd.inline(point1)||si5.da.inline(point1)){
                        System.out.println("on the quadrilateral");
                        return;
                    }
                    if(si5.insibian(point1)) {
                        System.out.println("in the quadrilateral");
                        return;
                    }
                    else{
                        System.out.println("outof the quadrilateral");
                        return;
                    }
                }
                else if (wu.ad.inline(point3)&&wu.ad.inline(point4)) {
                    Sanjiao san = new Sanjiao(point2, point5, point6);
                    if (san.gouchengsanjiao()) {
                        if (san.sa.inline(point1) || san.sb.inline(point1) || san.sc.inline(point1)) {
                            System.out.println("on the triangle");
                            return;
                        }
                        if (san.insanjiao(point1)) {
                            System.out.println("in the triangle");
                            return;
                        } else {
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                }
                else if (wu.ac.inline(point5)&&wu.ac.inline(point6)) {
                    Sanjiao san = new Sanjiao(point3, point4, point2);
                    if (san.gouchengsanjiao()) {
                        if (san.sa.inline(point1) || san.sb.inline(point1) || san.sc.inline(point1)) {
                            System.out.println("on the triangle");
                            return;
                        }
                        if (san.insanjiao(point1)) {
                            System.out.println("in the triangle");
                            return;
                        } else {
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                }
                else if (wu.bd.inline(point2)&&wu.bd.inline(point6)) {
                    Sanjiao san=new Sanjiao(point3,point4,point5);
                    if(san.gouchengsanjiao()){if (san.sa.inline(point1) || san.sb.inline(point1) || san.sc.inline(point1)) {
                        System.out.println("on the triangle");
                        return;
                    }
                        if (san.insanjiao(point1)) {
                            System.out.println("in the triangle");
                            return;
                        } else {
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                }
                else if (wu.be.inline(point5)&&wu.be.inline(point4)) {
                    Sanjiao san=new Sanjiao(point2,point3,point6);
                    if(san.gouchengsanjiao()){if (san.sa.inline(point1) || san.sb.inline(point1) || san.sc.inline(point1)) {
                        System.out.println("on the triangle");
                        return;
                    }
                        if (san.insanjiao(point1)) {
                            System.out.println("in the triangle");
                            return;
                        } else {
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                }
                else if (wu.ce.inline(point3)&&wu.ce.inline(point2)) {
                    Sanjiao san=new Sanjiao(point5,point6,point4);
                    if(san.gouchengsanjiao()){if (san.sa.inline(point1) || san.sb.inline(point1) || san.sc.inline(point1)) {
                        System.out.println("on the triangle");
                        return;
                    }
                        if (san.insanjiao(point1)) {
                            System.out.println("in the triangle");
                            return;
                        } else {
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                }
                else if (wu.ac.inline(point3)&&wu.ad.inline(point6)) {
                    Sanjiao san=new Sanjiao(point2,point4,point5);
                    if(san.gouchengsanjiao()){if (san.sa.inline(point1) || san.sb.inline(point1) || san.sc.inline(point1)) {
                        System.out.println("on the triangle");
                        return;
                    }
                        if (san.insanjiao(point1)) {
                            System.out.println("in the triangle");
                            return;
                        } else {
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                }
                else if (wu.bd.inline(point4)&&wu.be.inline(point2)) {
                    Sanjiao san=new Sanjiao(point3,point6,point5);
                    if(san.gouchengsanjiao()){if (san.sa.inline(point1) || san.sb.inline(point1) || san.sc.inline(point1)) {
                        System.out.println("on the triangle");
                        return;
                    }
                        if (san.insanjiao(point1)) {
                            System.out.println("in the triangle");
                            return;
                        } else {
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                }
                else if (wu.ac.inline(point3)&&wu.ce.inline(point5)) {
                    Sanjiao san=new Sanjiao(point2,point4,point6);
                    if(san.gouchengsanjiao()){if (san.sa.inline(point1) || san.sb.inline(point1) || san.sc.inline(point1)) {
                        System.out.println("on the triangle");
                        return;
                    }
                        if (san.insanjiao(point1)) {
                            System.out.println("in the triangle");
                            return;
                        } else {
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                }
                else if (wu.bd.inline(point4)&&wu.ad.inline(point6)) {
                    Sanjiao san=new Sanjiao(point2,point3,point5);
                    if(san.gouchengsanjiao()){if (san.sa.inline(point1) || san.sb.inline(point1) || san.sc.inline(point1)) {
                        System.out.println("on the triangle");
                        return;
                    }
                        if (san.insanjiao(point1)) {
                            System.out.println("in the triangle");
                            return;
                        } else {
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                }
                else if (wu.be.inline(point2)&&wu.ce.inline(point5)) {
                    Sanjiao san=new Sanjiao(point3,point4,point6);
                    if(san.gouchengsanjiao()){if (san.sa.inline(point1) || san.sb.inline(point1) || san.sc.inline(point1)) {
                        System.out.println("on the triangle");
                        return;
                    }
                        if (san.insanjiao(point1)) {
                            System.out.println("in the triangle");
                            return;
                        } else {
                            System.out.println("outof the triangle");
                            return;
                        }
                    }
                }
                break;
            }
        }
    }
    public static boolean geshi(String s){

        String s2= s.substring(0,2);
        if(!s2.matches("[1-6]\\:"))
        {
            System.out.println("Wrong Format");
            return false;
        }
        String s3 = s.substring(2);
        if(!s3.matches("([+|-]?(0|[1-9][0-9]*)(\\.\\d+)?,[+|-]?(0|[1-9][0-9]*)(\\.\\d+)?\\ ?)+"))
        {
            System.out.println("Wrong Format");
            return false;
        }
        return  true;
    }
    public static boolean dianshu(String s){
        String[] a = s.split(":");
        String[] b = a[1].split(" ");
        int n = b.length;
        if (s.charAt(0) == '1' && n != 5) {
            System.out.println("wrong number of points");
            return false;
        } else if (s.charAt(0) == '2' && n != 5) {
            System.out.println("wrong number of points");
            return false;
        } else if (s.charAt(0) == '3' && n != 7) {
            System.out.println("wrong number of points");
            return false;
        }
        else if (s.charAt(0) == '4' && n != 10) {
            System.out.println("wrong number of points");
            return false;
        }
        else if (s.charAt(0) == '5' && n != 10) {
            System.out.println("wrong number of points");
            return false;
        }
        else if (s.charAt(0) == '6' && n != 6) {
            System.out.println("wrong number of points");
            return false;
        }
        return  true;
    }
    static class Wubianxing {
        Point a,b,c,d,e;
        Line ab,bc,cd,de,ea,ac,ad,bd,be,ce;
        Wubianxing(Point a,Point b,Point c,Point d,Point e){
            this.a=a;this.b=b;this.c=c;this.d=d;this.e=e;
            this.ab=new Line(a,b);this.bc=new Line(b,c);this.cd=new Line(c,d);this.de=new Line(d,e);
            this.ea=new Line(e,a);this.ac=new Line(a,c);this.ad=new Line(a,d);this.bd=new Line(b,d);
            this.be=new Line(b,e);this.ce=new Line(c,e);
        }
        public boolean iswubianxing(){
            if(ab.pingxing(bc)||bc.pingxing(cd)||cd.pingxing(de)||de.pingxing(ea)){
                return false;
            }
            else if(Line.intersect(a.x,a.y,b.x,b.y,c.x,c.y,d.x,d.y)||Line.intersect(a.x,a.y,b.x,b.y,d.x,d.y,e.x,e.y)||
                    Line.intersect(b.x,b.y,c.x,c.y,d.x,d.y,e.x,e.y)||Line.intersect(b.x,b.y,c.x,c.y,e.x,e.y,a.x,a.y)||
                    Line.intersect(c.x,c.y,d.x,d.y,e.x,e.y,a.x,a.y))
                return false;

            return true;
        }
        public boolean istuwubianxing(){
            if((((b.x-a.x)*(c.y-b.y))-((c.x-b.x)*(b.y-a.y))>0&&((c.x-b.x)*(d.y-c.y))-((d.x-c.x)*(c.y-b.y))>0&&
                    ((d.x-c.x)*(e.y-d.y))-((e.x-d.x)*(d.y-c.y))>0&&((e.x-d.x)*(a.y-e.y))-((a.x-e.x)*(e.y-d.y))>0)||
                    (((b.x-a.x)*(c.y-b.y))-((c.x-b.x)*(b.y-a.y))<0&&((c.x-b.x)*(d.y-c.y))-((d.x-c.x)*(c.y-b.y))<0&&
                            ((d.x-c.x)*(e.y-d.y))-((e.x-d.x)*(d.y-c.y))<0&&((e.x-d.x)*(a.y-e.y))-((a.x-e.x)*(e.y-d.y))<0))
                return true;
            else
                return false;
        }
        public double zhouchang(){
            double c=this.ab.length()+this.bc.length()+this.cd.length()+this.de.length()+this.ea.length();
            double C=outformat(c);
            return  C;
        }
        public double area(){
            Sanjiao san1=new Sanjiao(this.a,this.b,this.c);Sanjiao san2=new Sanjiao(this.a,this.c,this.d);
            Sanjiao san3=new Sanjiao(this.a,this.d,this.e);
            double mj= san1.mianji()+ san2.mianji()+ san3.mianji();
            double mianji=outformat(mj);
            return mianji;
        }
        public Double outformat(double num) {
            if(num*1e+3%10!=0) {
                String num1=String.format("%.3f",num);
                return Double.valueOf(num1);
            }
            return num;
        }
        public boolean bianchonghe (Line l){
            if(this.ab.xianchonghe(l)){
                return true;
            }
            else if(this.bc.xianchonghe(l)){
                return true;
            }
            else if(this.cd.xianchonghe(l)){
                return true;
            }
            else if(this.de.xianchonghe(l)){
                return true;
            }
            else if(this.ea.xianchonghe(l)){
                return true;
            }
            return false;
        }
        public void fengewubainxing(Line l) {
            double area1=0,area2=0;

            if(this.ac.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.a,this.b,this.c);
                area1=ss1.mianji();
                area2=this.area()-area1;
                out(area1,area2);
            }
            else if(this.ad.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.a,this.d,this.e);
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.bd.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.b,this.d,this.c);
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.be.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.a,this.b,this.e);
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ce.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.c,this.d,this.e);
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ab.jiaodian(l)!=null&&this.bc.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.bc.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.ab.jiaodian(l),this.b,this.bc.jiaodian(l));
                area1= ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ab.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.ab.jiaodian(l),this.b,this.c,this.cd.jiaodian(l));
                ss1.otupanduan();
                area1= ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ab.jiaodian(l)!=null&&this.de.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.a,this.ab.jiaodian(l),this.de.jiaodian(l),this.e);
                ss1.otupanduan();
                area1= ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ab.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.ea.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.ab.jiaodian(l),this.a,this.ea.jiaodian(l));
                area1= ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.bc.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null&&this.bc.jiaodian(l)!=this.cd.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.bc.jiaodian(l),this.c,this.cd.jiaodian(l));
                area1= ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.bc.jiaodian(l)!=null&&this.de.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.bc.jiaodian(l),this.c,this.d,this.de.jiaodian(l));
                ss1.otupanduan();
                area1= ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.bc.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.bc.jiaodian(l),this.ea.jiaodian(l),this.a,this.b);
                ss1.otupanduan();
                area1= ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.cd.jiaodian(l)!=null&&this.de.jiaodian(l)!=null&&this.cd.jiaodian(l)!=this.de.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.cd.jiaodian(l),this.d,this.de.jiaodian(l));
                area1= ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.cd.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.cd.jiaodian(l),this.ea.jiaodian(l),this.e,this.d);
                ss1.otupanduan();
                area1= ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.de.jiaodian(l)!=null&&this.ea.jiaodian(l)!=null&&this.ea.jiaodian(l)!=this.de.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.ea.jiaodian(l),this.e,this.de.jiaodian(l));
                area1= ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else {
                System.out.println(0);
                System.exit(0);
            }
        }
        public void out(double m1,double m2){
            if(m1>=m2){
                System.out.println(2+" "+m2+" "+m1);
                System.exit(0);
            }
            else{
                System.out.println(2+" "+m1+" "+m2);
                System.exit(0);
            }
        }
        public boolean inwubianxing(Point p){
            Sanjiao ss1=new Sanjiao(this.a,this.b,p);Sanjiao ss2=new Sanjiao(this.b,this.c,p);
            Sanjiao ss3=new Sanjiao(this.c,this.d,p);Sanjiao ss4=new Sanjiao(this.d,this.e,p);
            Sanjiao ss5=new Sanjiao(this.e,this.a,p);
            if(Math.abs(this.area()-(ss1.mianji()+ss2.mianji()+ss3.mianji()+ss4.mianji()+ss5.mianji()))<0.0001)
                return true;
           else  return false;
        }
    }
    static class Line {
        Point x,y;

        Line (Point a, Point b){
            this.x=a;
            this.y=b;

        }
        double length(){
            return this.x.juli(this.y);
        }
        double distance(Point p){//!!!
            if(this.x.x==this.y.x){
                return  (p.x-this.x.x);

            }
            else{
                double e=(this.x.y-this.y.y)/(this.x.x-this.y.x);
                double b=this.x.y-(e*this.x.x);
                return (e*p.x-p.y+b)/Math.sqrt(e*e+1);
            }
        }
        public static boolean intersect(double l1x1,double l1y1,double l1x2,double l1y2,double l2x1,double l2y1,double l2x2,double l2y2) {

            // 快速排斥实验 首先判断两条线段在 x 以及 y 坐标的投影是否有重合。 有一个为真，则代表两线段必不可交。
            if (Math.max(l1x1,l1x2) < Math.min(l2x1 ,l2x2)
                    || Math.max(l1y1,l1y2) < Math.min(l2y1,l2y2)
                    || Math.max(l2x1,l2x2) < Math.min(l1x1,l1x2)
                    || Math.max(l2y1,l2y2) < Math.min(l1y1,l1y2))
            {
                return false;
            }
            // 跨立实验  如果相交则矢量叉积异号或为零，大于零则不相交
            else if ((((l1x1 - l2x1) * (l2y2 - l2y1) - (l1y1 - l2y1) * (l2x2 - l2x1))
                    * ((l1x2 - l2x1) * (l2y2 - l2y1) - (l1y2 - l2y1) * (l2x2 - l2x1))) > 0
                    || (((l2x1 - l1x1) * (l1y2 - l1y1) - (l2y1 - l1y1) * (l1x2 - l1x1))
                    * ((l2x2 - l1x1) * (l1y2 - l1y1) - (l2y2 - l1y1) * (l1x2 - l1x1))) > 0)
            {
                return false;
            }
            return true;
        }
        public double duijiaoxian() {
            double duijiaoxian=Math.sqrt((this.x.x-this.y.x)*(this.x.x-this.y.x)+(this.x.y-this.y.y)*(this.x.y-this.y.y));
            return duijiaoxian;
        }
        public boolean xianchonghe (Line l){
            return this.pingxing(l)&&l.distance(this.x)==0;
        }
        boolean inline(Point p){
            if(this.x.x==this.y.x&&this.y.x==p.x)
                return true;
            double e=(this.x.y-this.y.y)/(this.x.x-this.y.x);
            double b=this.x.y-(e*this.x.x);
            if((((e*p.x-p.y+b)==0&&(p.x>=min(x.x,y.x)&&p.x<=max(x.x,y.x)))&&((e*p.x-p.y+b)==0&&(p.y>=min(x.y,y.y)&&p.y<=max(x.y,y.y)))))
                return true;
            else
                return false;
        }
        Point jiaodian(Line l){
            Point v=sub(l.y,l.x);
            Point w=sub(this.y,this.x);
            Point p=l.x;
            Point q=this.x;
            Point u=sub(p,q);
            double t=cross(w,u)/cross(v,w);
            Point ans =new Point( p.x+v.x*t,p.y+v.y*t);
            double y0=ans.y;
            double x0=ans.x;
            if(((x0)>=min(x.x,y.x)&&(x0)<=max(x.x,y.x))&&((y0)>=min(x.y,y.y)&&(y0)<=max(x.y,y.y)))
                return ans;
            return null;

        }
        public static double cross (Point a, Point b){
            return a.x*b.y-a.y*b.x;
        }
        public static Point sub(Point a, Point b){
            return new Point(a.x-b.x,a.y-b.y);
        }
        boolean pingxing  (Line a){
            if((a.x.x==a.y.x )&&(this.x.x==this.y.x))
                return true;
            if((a.x.x==a.y.x)&&(this.x.x!=this.y.x))
                return false;
            if((a.x.x!=a.y.x)&&(this.x.x==this.y.x))
                return false;
            double e=a.x.xilv(a.y);
            double e1=this.x.xilv(this.y);
            if(e==e1)
                return true;
            else return false;
        }

    }
    static class Point {
        double x,y;
        Point(double a,double b){
            this.x=a;
            this.y=b;
        }
        public double getx(){
            return x;
        }
        public double gety(){
            return y;
        }
        public double juli(Point p){
            return Math.sqrt((this.x-p.x )*(this.x-p.x )+(this.y-p.y )*(this.y-p.y));
        }
        public double xilv(Point p){
            if(this.x==p.x){
                System.out.println("Slope does not exist");
                System.exit(0);
            }
            return (this.y-p.y)/(this.x-p.x);
        }
    }
    static class Sanjiao {
        Main.Point sx,sy,sz;
        Main.Line sa,sb,sc;
        Sanjiao (Main.Point a, Main.Point b, Main.Point c){
            this.sx=a;
            this.sy=b;
            this.sz=c;
            this.sa=new Main.Line(b,c);this.sb=new Main.Line(a,c);this.sc=new Main.Line(a,b);
        }
        public boolean gouchengsanjiao(){
            if(((this.sa.length()+this.sb.length())<=this.sc.length())||((this.sa.length()+this.sc.length())<=this.sb.length())||((this.sb.length()+this.sc.length())<=this.sa.length())){
                return false;
            }
            else return true;
        }

        public double zhouchang(){
            return (this.sa.length()+this.sb.length()+this.sc.length());
        }
        public double mianji(){
            double area=0;
            double s=(this.sa.length()+this.sb.length()+this.sc.length())/2;
            return area=Math.sqrt(s*(s-this.sa.length())*(s-this.sb.length())*(s-this.sc.length()));
        }
        public int type(){
            double[] num = new double[3];
            num[0] = this.sa.length();num[1] = this.sb.length();num[2] = this.sc.length();
            Arrays.sort(num);
            double tmp = Math.pow(num[0],2) + Math.pow(num[1],2) - Math.pow(num[2],2);
            if(Math.abs(tmp) < 0.0000001) return 1;
            if(tmp < 0) return 2;
            return 0;
        }
        public boolean insanjiao(Main.Point p){
            Sanjiao san1=new Sanjiao(p,sx,sy);Sanjiao san2=new Sanjiao(p,sy,sz);Sanjiao san3=new Sanjiao(p,sz,sx);
            double m1=san1.mianji();
            double m2=san2.mianji();
            double m3=san3.mianji();
            if(Math.abs(this.mianji()-(m1+m2+m3))<0.0001)
                return true;
            else return false;
        }
        public void fengesanjiaoxing(Line l){
            double area1=0,area2=0;
            if(this.sc.jiaodian(l)!=null&&this.sa.jiaodian(l)!=null&&this.sc.jiaodian(l)!=this.sa.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.sc.jiaodian(l),this.sy,this.sa.jiaodian(l));
                area1=ss1.mianji();
                area2=this.mianji()-area1;
                double mj1=outformat( area1);
                double mj2=outformat( area2);
                out(mj1,mj2);
            }
            else if(this.sc.jiaodian(l)!=null&&this.sb.jiaodian(l)!=null&&this.sc.jiaodian(l)!=this.sb.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.sc.jiaodian(l),this.sb.jiaodian(l),this.sx);
                area1=ss1.mianji();
                area2=this.mianji()-area1;
                double mj1=outformat( area1);
                double mj2=outformat( area2);
                out(mj1,mj2);
            }
            else if(this.sa.jiaodian(l)!=null&&this.sb.jiaodian(l)!=null&&this.sa.jiaodian(l)!=this.sb.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.sa.jiaodian(l),this.sz,this.sb.jiaodian(l));
                area1=ss1.mianji();
                area2=this.mianji()-area1;
                double mj1=outformat( area1);
                double mj2=outformat( area2);
                out(mj1,mj2);
            }
            else {
                System.out.println(0);
                System.exit(0);
            }
        }
        public Double outformat(double num) {
            if(num*1e+3%10!=0) {
                String num1=String.format("%.3f",num);
                return Double.valueOf(num1);
            }
            return num;
        }
        public void out(double m1,double m2){
            if(m1>=m2){
                System.out.println(2+" "+m2+" "+m1);
                System.exit(0);
            }
            else{
                System.out.println(2+" "+m1+" "+m2);
                System.exit(0);
            }
        }
        public boolean bianchonghe(Line l){
            if(this.sa.xianchonghe(l))
                return false;
            else if(this.sb.xianchonghe(l))
                return false;
            else if(this.sc.xianchonghe(l))
                return  false;
            else
                return true;
        }
    }
    static class Sibian {
        Main.Point a,b,c,d;
        Main.Line ab,bc,cd,da,ac,bd;
        private boolean judge1=false;//0,2
        private boolean judge2=false;//1,3
        Sibian(Main.Point a, Main.Point b, Main.Point c, Main.Point d){
            this.a=a;this.b=b;this.c=c;this.d=d;
            this.ab=new Main.Line(a,b);this.bc=new Main.Line(b,c);this.cd=new Main.Line(c,d);
            this.da=new Main.Line(d,a);this.ac=new Main.Line(a,c);this.bd=new Main.Line(b,d);
        }
        public void sibianxing(){
            if(Math.abs((a.y-c.y)*(a.x-b.x)-(a.y-b.y)*(a.x-c.x))<1e-6||
                    Math.abs((a.y-d.y)*(a.x-b.x)-(a.y-b.y)*(a.x-d.x))<1e-6||
                    Math.abs((a.y-d.y)*(a.x-c.x)-(a.y-c.y)*(a.x-d.x))<1e-6||
                    Math.abs((b.y-d.y)*(b.x-c.x)-(b.y-c.y)*(b.x-d.x))<1e-6)System.out.print("false ");
            else {
                if(!Main.Line.intersect(a.x,a.y,d.x,d.y,b.x,b.y,c.x,c.y)) {
                    System.out.print("true ");
                }
                else System.out.print("false ");
            }
        }
        public void pingxingsibianxing(){
            if(this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length())System.out.print("true");
            else System.out.print("false");
        }
        public boolean nengfougoucheng(){
            if(Math.abs((a.y-c.y)*(a.x-b.x)-(a.y-b.y)*(a.x-c.x))<1e-6||
                    Math.abs((a.y-d.y)*(a.x-b.x)-(a.y-b.y)*(a.x-d.x))<1e-6||
                    Math.abs((a.y-d.y)*(a.x-c.x)-(a.y-c.y)*(a.x-d.x))<1e-6||
                    Math.abs((b.y-d.y)*(b.x-c.x)-(b.y-c.y)*(b.x-d.x))<1e-6) {
                return false;
            }
            else return !Main.Line.intersect(a.x, a.y, d.x, d.y, b.x, b.y, c.x, c.y) && !Main.Line.intersect(a.x, a.y, b.x, b.y, d.x, d.y, c.x, c.y);
        }
        public boolean lingxing(){
            return (this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length());
        }
        public boolean changfangxing(){
            Main.Line l1=new Main.Line(a,c);
            double ac=l1.duijiaoxian();
            Main.Line l2=new Main.Line(b,d);
            double bd=l2.duijiaoxian();
            return (ac==bd&&this.ab.length()==this.cd.length()&&this.bc.length()==this.da.length());
        }
        public boolean zhengfangxing(){
            return (lingxing()&& changfangxing());
        }
        public boolean otupanduan() {
            Main.Line l1=new Main.Line(a,c);
            double distance1=l1.distance(b);
            double distance2=l1.distance(d);
            Main.Line l2=new Main.Line(b,d);
            double distance3=l2.distance(a);
            double distance4= l2.distance(c);
            if(distance1*distance2<0)judge1=true;
            if(distance3*distance4<0)judge2=true;
            if(judge1==true&&judge2==true) {
                return true;
            }
            return false;
        }
        public double zhouchang() {
            double ab=this.ab.length();
            double bc=this.bc.length();
            double cd=this.cd.length();
            double da=this.da.length();
            double c=ab+bc+cd+da;
            double C=outformat(c);
            return C;
        }
        public double area() {
            double area=0;
            double area1=0;
            double area2=0;
            double are=0;
            //凸四边形
            if(judge1==true&&judge2==true) {
                area1=Math.abs((b.x*c.y+c.x*d.y+d.x*b.y-b.x*d.y-c.x*b.y-d.x*c.y)/2);
                area2=Math.abs((b.x*a.y+a.x*d.y+d.x*b.y-b.x*d.y-a.x*b.y-d.x*a.y)/2);
                area=area1+area2;
                are= outformat(area);
            }
            else if(judge1==false) {
                area1=Math.abs((b.x*d.y+d.x*a.y+a.x*b.y-b.x*a.y-d.x*b.y-a.x*d.y)/2);
                area2=Math.abs((d.x*c.y+c.x*b.y+b.x*d.y-d.x*b.y-c.x*d.y-b.x*c.y)/2);
                area=area1+area2;
                are= outformat(area);
            }
            else if(judge2==false) {
                area1=Math.abs((b.x*c.y+c.x*a.y+a.x*b.y-b.x*a.y-c.x*b.y-a.x*c.y)/2);
                area2=Math.abs((d.x*c.y+c.x*a.y+a.x*d.y-d.x*a.y-c.x*d.y-a.x*c.y)/2);
                area=area1+area2;
                are=outformat(area);
            }
            return are;
        }
        public Double outformat(double num) {
            if(num*1e+3%10!=0) {
                String num1=String.format("%.3f",num);
                return Double.valueOf(num1);
            }
            return num;
        }
        public boolean bianchonghe (Main.Line l){
            if(this.ab.xianchonghe(l)){
                return true;
            }
            else if(this.bc.xianchonghe(l)){
                return true;
            }
            else if(this.cd.xianchonghe(l)){
                return true;
            }
            else if(this.da.xianchonghe(l)){
                return true;
            }
            return false;
        }
        public boolean insibian(Main.Point p){
            double m=0;
            if(otupanduan()){
                m=area();
            }

            Main.Sanjiao ss1=new Main.Sanjiao(p,a,b);
            Main.Sanjiao ss2=new Main.Sanjiao(p,b,c);
            Main.Sanjiao ss3=new Main.Sanjiao(p,c,d);
            Main.Sanjiao ss4=new Main.Sanjiao(p,d,a);
            double m1=ss1.mianji();
            double m2=ss2.mianji();
            double m3=ss3.mianji();
            double m4=ss4.mianji();
            if(Math.abs(m-(m1+m2+m3+m4))<0.0001)/*注意一定要三位小数或更多，不然通不过测试点*/
                return true;
            else return false;
        }
        public void fengesibianxing(Line l){
            double area1=0,area2=0;
            if(this.ac.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.a,this.b,this.c);
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.bd.xianchonghe(l)){
                Sanjiao ss1=new Sanjiao(this.a,this.b,this.d);
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ab.jiaodian(l)!=null&&this.bc.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.bc.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.ab.jiaodian(l),this.b,this.bc.jiaodian(l));
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ab.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.a,this.ab.jiaodian(l),this.cd.jiaodian(l),this.d);
                area1=ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.ab.jiaodian(l)!=null&&this.da.jiaodian(l)!=null&&this.ab.jiaodian(l)!=this.da.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.a,this.ab.jiaodian(l),this.da.jiaodian(l));
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.bc.jiaodian(l)!=null&&this.cd.jiaodian(l)!=null&&this.bc.jiaodian(l)!=this.cd.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.bc.jiaodian(l),this.c,this.cd.jiaodian(l));
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.bc.jiaodian(l)!=null&&this.da.jiaodian(l)!=null){
                Sibian ss1=new Sibian(this.a,this.b,this.bc.jiaodian(l),this.da.jiaodian(l));
                area1=ss1.area();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else if(this.cd.jiaodian(l)!=null&&this.da.jiaodian(l)!=null&&this.da.jiaodian(l)!=this.cd.jiaodian(l)){
                Sanjiao ss1=new Sanjiao(this.da.jiaodian(l),this.d,this.cd.jiaodian(l));
                area1=ss1.mianji();
                area2=this.area()-area1;
                double mj1= outformat(area1);
                double mj2= outformat(area2);
                out(mj1,mj2);
            }
            else {
                System.out.println(0);
                System.exit(0);
            }
        }
        public void out(double m1,double m2){
            if(m1>=m2){
                System.out.println(2+" "+m2+" "+m1);
                System.exit(0);
            }
            else{
                System.out.println(2+" "+m1+" "+m2);
                System.exit(0);
            }
        }
    }


}

View Code

圈复杂度分析：

 

 

 

 

 

 

优缺点：

优点：1.对每个方法的计算严谨，尽量减少了存在的误差。

2.使用了面向过程，创建多个类，进行协同完成，减少了代码冗余。

缺点：1.在构造点和线且赋值的时候繁琐，容易出现混乱。

2.由于时间和水平的有限，没能完成全部的选项。

3.没有用到继承和重载的方法，代码冗余还是有些多。

4.没有使用更好的方法，例如数组，再构造点的时候出现了大量的相同代码，出现混乱。

期中考试：

7-1 点与线（类设计）

• 设计一个类表示平面直角坐标系上的点Point，私有属性分别为横坐标x与纵坐标y，数据类型均为实型数，除构造方法以及属性的getter与setter方法外，定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息，格式如下：(x,y)，数值保留两位小数。为简化题目，其中，坐标点的取值范围设定为(0,200]。若输入有误，系统则直接输出Wrong Format

• 设计一个类表示平面直角坐标系上的线Line，私有属性除了标识线段两端的点point1、point2外，还有一个字符串类型的color，用于表示该线段的颜色，同样，除构造方法以及属性的getter与setter方法外，定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息，输出格式如下：

    ```
        The line's color is:颜色值
        The line's begin point's Coordinate is:
        (x1,y1)
        The line's end point's Coordinate is:
        (x2,y2)
        The line's length is:长度值
    ```
  

   

  其中，所有数值均保留两位小数，建议可用String.format("%.2f", data)方法。

    设计类图如下图所示。
  

   

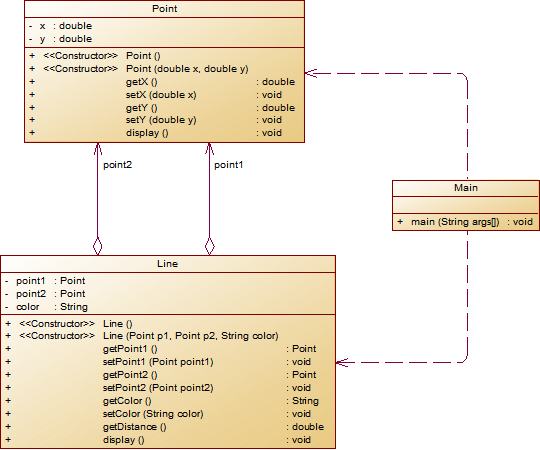
** 题目要求：在主方法中定义一条线段对象，从键盘输入该线段的起点坐标与终点坐标以及颜色，然后调用该线段的display()方法进行输出。**

• 以下情况为无效作业
  • 无法运行
  • 设计不符合所给类图要求
  • 未通过任何测试点测试
  • 判定为抄袭

输入格式:

分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色，中间可用一个或多个空格、tab或者回车分隔。

输出格式:

The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值

主要思路：这次考试题目相对来说难度不大，比较简单，按照老师给的类图写出类及其拥有的属性和方法，一定要仔细，多看几遍类图。再进行调用，就可以完成此次作业。

主要代码：

import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
       Scanner input=new Scanner(System.in);
        double x1,x2,y1,y2;
        String color;
        x1=input.nextDouble();
        y1=input.nextDouble();
        x2=input.nextDouble();
        y2=input.nextDouble();
        if(x1>0&&x1<=200&&y1>0&&y1<=200&&x2>0&&x2<=200&&y2>0&&y2<=200)
        {
            Point point1=new Point(x1,y1);
            Point point2=new Point(x2,y2);
            color=input.next();
            Line line1=new Line(point1,point2,color);
            line1.display();
        }
        else
        {
            System.out.println("Wrong Format");
            System.exit(0);
        }
    }
}
class Point {
    private double x;
    private double y;
    Point(){

    }
    Point(double x,double y){
        this.x=x;
        this.y=y;
    }
    public double getX(){
        return x;
    }
    public void  setX(double x){
        this.x=x;
    }
    public double getY(){
        return y;
    }
    public void setY(double y){
        this.y=y;
    }
    public void display(){
        System.out.println("("+String.format("%.2f", getX())+","+String.format("%.2f", getY()));
    }
}
class Line {
    private Point point1=new Point();
    private Point point2=new Point();
    private String color;
    Line (){

    }
    Line(Point point1,Point point2,String color){
        this.point1=point1;
        this.point2=point2;
        this.color=color;
    }
    public Point getPoint1(){
        return point1;
    }
    public void setPoint1(Point point1){
        this.point1=point1;
    }
    public Point getPoint2(){
        return point2;
    }
    public void setPoint2(Point point2){
        this.point2=point2;
    }
    public String getColor(){
        return color;
    }
    public void setColor(String color){
        this.color=color;
    }

    public double getDistance()
    {
        return Math.sqrt((point1.getX()-point2.getX())*(point1.getX()-point2.getX())+(point1.getY()-point2.getY())*(point1.getY()-point2.getY()));
    }
    public void display(){
        System.out.println("The line's color is:"+color);
        System.out.println("The line's begin point's Coordinate is:");
        System.out.println("("+String.format("%.2f",point1.getX())+","+String.format("%.2f",point1.getY())+")");
        System.out.println("The line's end point's Coordinate is:");
        System.out.println("("+String.format("%.2f",point2.getX())+","+String.format("%.2f",point2.getY())+")");
        System.out.printf("The line's length is:");
        System.out.printf("%.2f\n",getDistance());
    }
}

View Code

圈复杂度分析：

 

 

 

7-2 点线面问题重构（继承与多态）

在“点与线（类设计）”题目基础上，对题目的类设计进行重构，以实现继承与多态的技术性需求。

• 对题目中的点Point类和线Line类进行进一步抽象，定义一个两个类的共同父类Element（抽象类），将display()方法在该方法中进行声明（抽象方法），将Point类和Line类作为该类的子类。
• 再定义一个Element类的子类面Plane，该类只有一个私有属性颜色color，除了构造方法和属性的getter、setter方法外，display()方法用于输出面的颜色，输出格式如下：The Plane's color is:颜色
• 在主方法内，定义两个Point（线段的起点和终点）对象、一个Line对象和一个Plane对象，依次从键盘输入两个Point对象的起点、终点坐标和颜色值（Line对象和Plane对象颜色相同），然后定义一个Element类的引用，分别使用该引用调用以上四个对象的display()方法，从而实现多态特性。示例代码如下：

        element = p1;//起点Point
        element.display();
        
        element = p2;//终点Point
        element.display();
        
        element = line;//线段
        element.display();
        
        element = plane;//面
        element.display();
  

    类结构如下图所示。

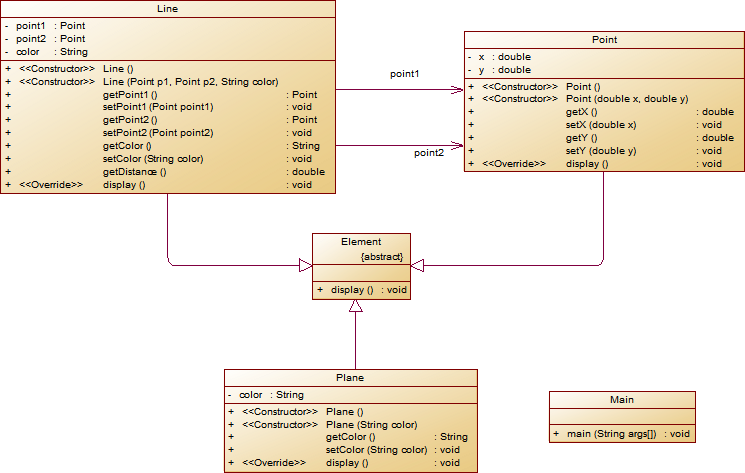
其中，所有数值均保留两位小数，建议可用String.format("%.2f", data)方法。

• 以下情况为无效作业
  • 无法运行
  • 设计不符合所给类图要求
  • 未通过任何测试点测试
  • 判定为抄袭

输入格式:

分别输入线段的起点横坐标、纵坐标、终点的横坐标、纵坐标以及颜色，中间可用一个或多个空格、tab或者回车分隔。

输出格式:

(x1,y1)
(x2,y2)
The line's color is:颜色值
The line's begin point's Coordinate is:
(x1,y1)
The line's end point's Coordinate is:
(x2,y2)
The line's length is:长度值
The Plane's color is:颜色值

主要思路：按照老师给的类图写出类及其拥有的属性和方法，再第一题的基础想再加两个类，再进行调用，就可以完成此次作业。
主要代码：

import java.util.Scanner;
import static java.lang.Math.sqrt;
public class Main
{
    public static void main(String[] args)
    {
        Scanner input=new Scanner(System.in);
        double x1,x2,y1,y2;
        String color;
        x1=input.nextDouble();
        y1=input.nextDouble();
        x2=input.nextDouble();
        y2=input.nextDouble();
        if(x1>0&&x1<=200&&y1>0&&y1<=200&&x2>0&&x2<=200&&y2>0&&y2<=200)
        {
            Point point1=new Point(x1,y1);
            Point point2=new Point(x2,y2);
            color=input.next();
            Line line1=new Line(point1,point2,color);
            Plane plane=new Plane(color);
            Element element;
            element = point1;//起点Point
            element.display();

            element = point2;//终点Point
            element.display();

            element = line1;//线段
            element.display();

            element = plane;//面
            element.display();
        }
        else
        {
            System.out.println("Wrong Format");
        }
    }
}
class Point extends Element{

        private double x;
        private double y;
        Point(){

        }
        Point(double x,double y){
            this.x=x;
            this.y=y;
        }
        public double getX(){
            return x;
        }
        public void  setX(double x){
            this.x=x;
        }
        public double getY(){
            return y;
        }
        public void setY(double y){
            this.y=y;
        }
        public void display(){
            System.out.println("("+String.format("%.2f", getX())+","+String.format("%.2f", getY())+")");
        }


}
 class Line extends Element{
    private Point point1=new Point();
    private Point point2=new Point();
    private String color;
    Line (){

    }
    Line(Point point1,Point point2,String color){
        this.point1=point1;
        this.point2=point2;
        this.color=color;
    }
    public Point getPoint1(){
        return point1;
    }
    public void setPoint1(Point point1){
        this.point1=point1;
    }
    public Point getPoint2(){
        return point2;
    }
    public void setPoint2(Point point2){
        this.point2=point2;
    }
    public String getColor(){
        return color;
    }
    public void setColor(String color){
        this.color=color;
    }

    public double getDistance()
    {
        return Math.sqrt((point1.getX()-point2.getX())*(point1.getX()-point2.getX())+(point1.getY()-point2.getY())*(point1.getY()-point2.getY()));
    }
    public void display(){
        System.out.println("The line's color is:"+color);
        System.out.println("The line's begin point's Coordinate is:");
        System.out.println("("+String.format("%.2f",point1.getX())+","+String.format("%.2f",point1.getY())+")");
        System.out.println("The line's end point's Coordinate is:");
        System.out.println("("+String.format("%.2f",point2.getX())+","+String.format("%.2f",point2.getY())+")");
        System.out.printf("The line's length is:");
        System.out.printf("%.2f\n",getDistance());
    }
}
 class Plane extends Element {
    private String color;
    Plane(){

    }
    Plane(String color){
        this.color=color;
    }
    public String getColor(){
        return  color;
    }
    public void setColor(String color){
        this.color=color;
    }
    public void display(){
        System.out.println("The Plane's color is:"+color);
    }
}
 abstract class Element {
    public void display(){

    }
}

View Code 圈复杂度分析：

 

 

 

7-3 点线面问题再重构（容器类）

在“点与线（继承与多态）”题目基础上，对题目的类设计进行重构，增加容器类保存点、线、面对象，并对该容器进行相应增、删、遍历操作。

• 在原有类设计的基础上，增加一个GeometryObject容器类，其属性为ArrayList<Element>类型的对象（若不了解泛型，可以不使用<Element>）
• 增加该类的add()方法及remove(int index)方法，其功能分别为向容器中增加对象及删除第index - 1（ArrayList中index>=0）个对象
• 在主方法中，用户循环输入要进行的操作（choice∈[0,4]），其含义如下：
  • 1：向容器中增加Point对象
  • 2：向容器中增加Line对象
  • 3：向容器中增加Plane对象
  • 4：删除容器中第index - 1个数据，若index数据非法，则无视此操作
  • 0：输入结束
  示例代码如下：

     choice = input.nextInt();
      while(choice != 0) {
          switch(choice) {
          case 1://insert Point object into list 
            ...
              break;
          case 2://insert Line object into list
              ...
              break;
          case 3://insert Plane object into list
              ...
              break;
          case 4://delete index - 1 object from list
              int index = input.nextInt();
              ...
          }
          choice = input.nextInt();
      }
  

    输入结束后，按容器中的对象顺序分别调用每个对象的display()方法进行输出。
  类图如下所示：

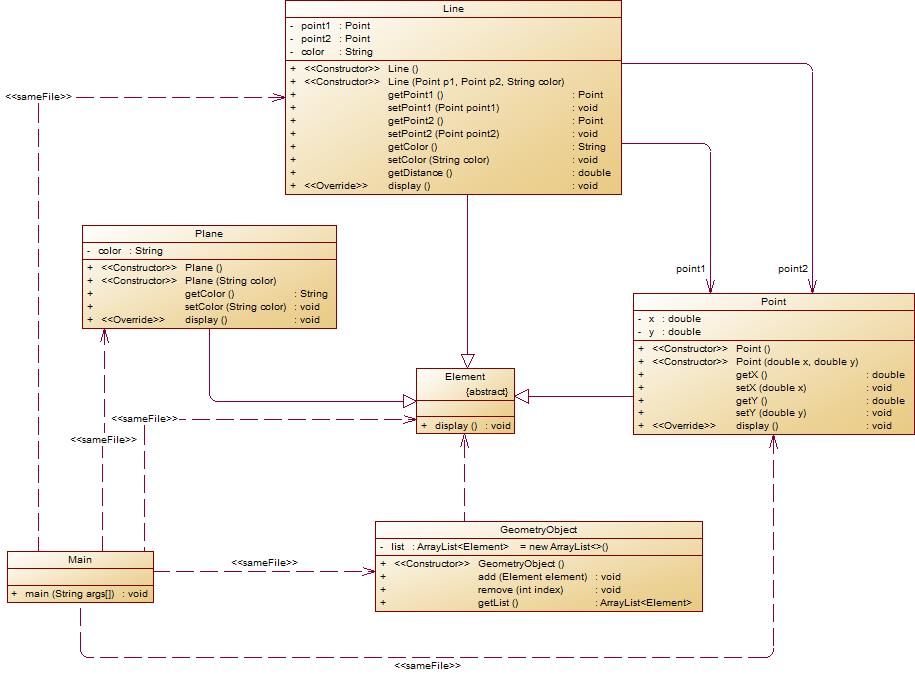
• 以下情况为无效作业
  • 无法运行
  • 设计不符合所给类图要求
  • 未通过任何测试点测试
  • 判定为抄袭

输入格式:

switch(choice) {
            case 1://insert Point object into list 
              输入“点”对象的x，y值
                break;
            case 2://insert Line object into list
                输入“线”对象两个端点的x，y值
                break;
            case 3://insert Plane object into list
                输入“面”对象的颜色值
                break;
            case 4://delete index - 1 object from list
                输入要删除的对象位置（从1开始）
                ...
            }

 

输出格式:

• Point、Line、Plane的输出参考题目2
• 删除对象时，若输入的index超出合法范围，程序自动忽略该操作

代码思路：在前两题的基础上按照给出的类图及其属性，方法添加相应的类，熟悉的使用ArrayList<Element>类型，做出此题还是比较轻松。

主要代码：

import java.util.Scanner;
import java.util.ArrayList;
public class Main
{
    public static void main(String[] args)
    {
        Scanner input=new Scanner(System.in);
        double x1,x2,y1,y2;
        int choice=0;
        int index;
        String color;
        GeometryObject geometryObject=new GeometryObject();
        choice=input.nextInt();
        while(choice!=0)
        {
            switch(choice)
            {
                case 1:{
                    x1=input.nextDouble();
                    y1=input.nextDouble();
                    Point p = new Point(x1,y1);
                    geometryObject.add(p);
                }
                break;
                case 2:{
                    x1=input.nextDouble();
                    y1=input.nextDouble();
                    Point p1 = new Point(x1,y1);
                    x2=input.nextDouble();
                    y2=input.nextDouble();
                    Point p2 = new Point(x2,y2);
                    color = input.next();
                    Line l = new Line(p1,p2,color);
                    geometryObject.add(l);

                }
                break;
                case 3:
                {
                    color = input.next();
                    Plane p = new Plane(color);
                    geometryObject.add(p);
                }
                break;
                case 4:
                {
                    index = input.nextInt();
                    if(geometryObject.getList().size()>=index)
                        geometryObject.remove(index-1);
                }
            }
            choice = input.nextInt();
        }
        ArrayList<Element> list = geometryObject.getList();
        for(int i=0;i<list.size();i++)
        {
            list.get(i).display();
        }
    }
}
class GeometryObject
{
    ArrayList<Element> list=new ArrayList<>();

    public GeometryObject() {

   }
    public GeometryObject(ArrayList<Element> list) {
        this.list = list;
    }
    public ArrayList<Element> getList() {
        return list;
    }

    public void setList(ArrayList<Element> list) {
        this.list = list;
    }
    public void add(Element e)
    {
        list.add(e);
    }
    public void remove(int n)
    {
        list.remove(n);
    }
}
class Point extends Element{

    private double x;
    private double y;
    Point(){

    }
    Point(double x,double y){
        this.x=x;
        this.y=y;
    }
    public double getX(){
        return x;
    }
    public void  setX(double x){
        this.x=x;
    }
    public double getY(){
        return y;
    }
    public void setY(double y){
        this.y=y;
    }
    public void display(){
        System.out.println("("+String.format("%.2f", getX())+","+String.format("%.2f", getY())+")");
    }


}
class Line extends Element{
    private Point point1=new Point();
    private Point point2=new Point();
    private String color;
    Line (){

    }
    Line(Point point1,Point point2,String color){
        this.point1=point1;
        this.point2=point2;
        this.color=color;
    }
    public Point getPoint1(){
        return point1;
    }
    public void setPoint1(Point point1){
        this.point1=point1;
    }
    public Point getPoint2(){
        return point2;
    }
    public void setPoint2(Point point2){
        this.point2=point2;
    }
    public String getColor(){
        return color;
    }
    public void setColor(String color){
        this.color=color;
    }

    public double getDistance()
    {
        return Math.sqrt((point1.getX()-point2.getX())*(point1.getX()-point2.getX())+(point1.getY()-point2.getY())*(point1.getY()-point2.getY()));
    }
    public void display(){
        System.out.println("The line's color is:"+color);
        System.out.println("The line's begin point's Coordinate is:");
        System.out.println("("+String.format("%.2f",point1.getX())+","+String.format("%.2f",point1.getY())+")");
        System.out.println("The line's end point's Coordinate is:");
        System.out.println("("+String.format("%.2f",point2.getX())+","+String.format("%.2f",point2.getY())+")");
        System.out.printf("The line's length is:");
        System.out.printf("%.2f\n",getDistance());
    }
}
 class Plane extends Element {
    private String color;
    Plane(){

    }
    Plane(String color){
        this.color=color;
    }
    public String getColor(){
        return  color;
    }
    public void setColor(String color){
        this.color=color;
    }
    public void display(){
        System.out.println("The Plane's color is:"+color);
    }
}
abstract class Element {
    public void display(){

    }
}

View Code

圈复杂度分析：

 

 

三、踩坑心得：

1.在题目集四中第一题中在一串字符串中提取出数字时，当时自然想到了substring()方法，但是结果不是这样，要用到正则表达式，才会得出正确的结果；第二题中四边形也是让人头疼的一道题，我将判断格式输入是否正确的判断封装成一个类，在主类中调用的时候总是有两个点通不过，但将这个判断的方法放在主类中时，测试点都会通过。还有求线段的焦点时这次要用向量法来解决，不然通不过，也可能是我前面的写错了还是什么，就是通不过。在判断点是否在多边形中时，我用了等面积法，但在用的过程中由于double类型的要求，会有精度，在判断相等时要用到<0.00001，而且不能<0.1，这样精度不准确，造成判断错误，得不出正确的结果。在第三题中逐行接受刚开始没注意，写完代码发现只输出了一条结果，完了才发现是逐行接收，还有一i的那个要记住字符串的比较一i的那个要用equal()函数，不能用==，还有在输入密码错误后，不能System.exit(0)，否则会退出整个程序，不能进行下面的操作。还有一定要注意输出的格式。

2.在题目集五中，主要的还是等面积发判断是否在多边形类中的数字精度的问题，但在用的过程中由于double类型的要求，会有精度，在判断相等时要用到<0.00001，而且不能<0.1，这样精度不准确，造成判断错误，得不出正确的结果。还有最重要的一点是提前没有规划好，没有用数组，导致十个点时，要创建多个点，这样出现了混乱，也要考虑好多种情况，让自己脑子有点乱。

3.在期中考试的时候题目比较简单，但在唯一的不足就是自己的粗心吧，在输出的时候没有将点括号括起来，导致结果一直是错的，但结果是正确。

四、改进建议：

       根据圈复杂度的计算方法，发现我这几次的代码感觉的还是有点复杂了，尤其是题目集四和题目集五中四边形和五边形的构造中考虑的情况越来越多，像五边形后面3，4，5，6选项都要只要十二次的选择，导致用了大量的if-else语句，提高了圈复杂度。遇到这样的情况要提前考虑好怎么解决这个题目，就像这次题目集四、五用数组会明显地减少代码，以及相应的选择代码。下次作业我尽量少写if-else，多写switch，case减少复杂度，而且每一题尽量使用面向对象的思路，多分类和把每个方法都写的简洁明了。由SourceMonitor的评测图结果可以可知，题目集四、五中每个题目的圈复杂度之高，因为使用的是普通的if-else语句，并且类设计的也是出现了大量的相同代码，大致跟面向过程差不多，在以后的学习中，做此类题目应该使用正则表达式降低代码繁杂和复杂度，也要多将类与类之间的关系进行调用，体现java面向对象的特点。

五、总结：

        通过一段对java的学习，发现自己对java的基础知识有很多的欠缺，基础的知识还是有些不知道，需要继续努力的学习，总是出现bug，但是还是只能静下心来一点一点的学习，请教同学和网上搜集资料，只有学好这些基础的类知识，才能为后面更好的学习做准备，需要学习更多的结构、语法知识来充实java的学习。在优化代码和减少复杂度的方面有所欠缺，需要在这方面改进。上课认真听课，课后也需要自己多了解java的知识，许多知识还需要自学，多巩固基础函数语法知识，更易于理解和吸收，防止在平常编写代码时忘记一些基础知识。要学会在解决一道题时，提前考虑好要用什么方法才能更好的解决这个问题，才能更好的优化此题。

 

标签：JAVA,Point,期中考试,double,return,System,Blog,inline,new
From： https://www.cnblogs.com/11100927A/p/16836543.html