D. Dark LaTeX vs. Light LaTeX
The 2023 ICPC Asia Shenyang Regional Contest (The 2nd Universal Cup. Stage 13: Shenyang)
给两个字符串 \(s,t\),长度分别为 \(n,m\),现在分别取 \(s,t\) 的子串 \(s',t'\),合成一个新的长度为偶数的字符串 \(str=s'+t'\),记 \(str\) 的长度为 \(2k\),问有多少种取字符串的方法使得 \(str_{1\sim k}=str_{k+1,2k}\)。
sample
input: output: abab 8 ab\((1,1,1,1)(1,1,1,1), (1,2,1,2)(1,2,1,2), (1,3,2,2)(1,3,2,2), (2,2,2,2)(2,2,2,2)\)
\(n,m\leq 5\times 10^3\)
不妨先假设 \(str\) 至少半部分都属于 \(s\) 串,即 \(str_{1\sim p}=s',p\in[k,2k-1]\)。如果 \(str\) 串只有前小半部分属于 \(s\) 串,即 \(str_{1\sim p}=s',p\in[1,k-1]\),那么可以将两个串先前后翻转,再将 \(s\) 串作为 \(t\) 串,\(t\) 串作为 \(s\) 串,执行前多半部分属于 \(s\) 串的操作;同时会发现 \(str_{1\sim k}=s'=str_{k+1,2k}=t'\) 的情况会考虑两次,可以单独减去(具体实现就不讲了)。
懒得画多个图了,所以可能思维比较跳跃,将就着看了
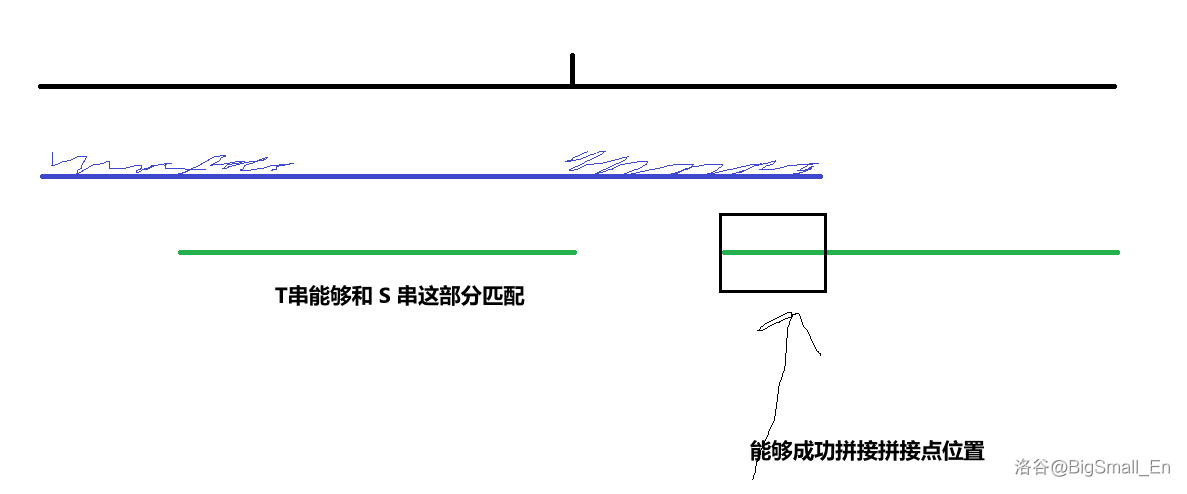
由于 \(s'\) 占据了整个 \(str_{1\sim k}\) 和 \(str_{k+1\sim 2k}\) 的一个前缀,这个前缀必然要和 \(str_{1\sim k}\) 的一个前缀完全匹配。而 \(t'\) 显然要与 \(str_{1\sim k}\) 的一个后缀能够匹配,这个后缀存在于 \(s\) 中,同时需要 \(匹配前缀长+ 匹配后缀长\geq k\) ,这样才能拼接合法。至此我们明确了合法的构造方法。
记 \(f_{i,j}\) 为 \(s_{i\sim n}\) 和 \(s_{j\sim n}\) 的最长公共前缀,\(g_{i,j}\) 为 \(s_{1\sim i}\) 和 \(t_{1,j}\) 的最长公共后缀,我们可以通过 \(O(n^2)\) DP预处理出两者。
\[f_{i,j}=f_{i+1,j+1}+[s_i=s_j] \]\[g_{i,j}=g_{i-1,j-1}+[s_i=t_j] \]直接枚举 \(s\) 的一个子串 \(s_{i\sim j}\) 作为 \(str_{1\sim k}\),\(f_{i,j+1}\) 图中蓝色波浪的长度(即 \(k=j-i+1\)),他限制了 \(t'\) 串与 \(str_{1,k}=s_{i,j}\) 匹配的最小长度。同时我们让 \(t_{1\sim p}\) 与 \(str_{1\sim k}\) 进行后缀的匹配,\(g_{j,p}\) 为图中绿串的长度。能够成功拼接的方案数就是 \(\min(f_{i,j+1}+g_{j,p}-k+1,f_{i,j+1}+1)\)。
这样枚举 \(i,j,p\),我们就得到了一个 \(O(n^3)\) 的算法。考虑进行优化。
可以先枚举 \(j\),枚举 \(p\) 将 \(g_{j,p}\) 放入“数据结构”中,再在枚举 \(i\) 的时候 \(O(1)\) 地统计每个所有 \(p\) 的答案。这个问题只需要维护两个前缀和即可
\[s_p=\sum_{i=1}^{m}g_{j,p}\\ \]\[b_p=\sum_{i=1}^{m}[g_{j,p}>0] \]每个 \(i\) 的答案
\[\begin{align} ans&=\sum_{p=1}^{m}\min(f_{i,j+1}+g_{j,p}-k+1,f_{i,j+1}+1)[g_{j,p}\geq k-f_{i,j+1}]\\ &=\sum_{p=1}^{m}(f_{i,j+1}+1)[g_{j,p}>k]+\sum_{p=1}^{m}(f_{i,j+1}+g_{j,p}-k+1)[k\geq g_{j,p}\geq k-f_{i,j+1}]\\ &=(b_{m}-b_{k})\times (f_{i,j+1}+1)+(b_k-b_{k-{f_{i,j+1}-1}})\times (f_{i,j+1}-k+1)+(s_k-s_{k-f_{i,j+1}-1}) \end{align} \]具体实现见代码吧,快下课了
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||'9'<ch){if(ch=='-')f=-1;ch=getchar();}
while('0'<=ch&&ch<='9'){x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*f;
}
const int N=5003;
char s[N],t[N],z[N];
int n,m,f[N][N],g[N][N];
ll ans=0,sumn[N],suml[N];
inline void solve(int flag){
memset(f,0,sizeof(f));
memset(g,0,sizeof(g));
memset(sumn,0,sizeof(sumn));
memset(suml,0,sizeof(suml));
for(int i=n;i>=1;--i){
for(int j=n;j>=1;--j){
if(s[i]==s[j])
f[i][j]=f[i+1][j+1]+1;
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j)
if(s[i]==t[j])
g[i][j]=g[i-1][j-1]+1;
}
for(int i=1;i<=n;++i){
for(int j=0;j<=m;++j)
sumn[j]=suml[j]=0;
for(int j=1;j<=m;++j){
if(!g[i][j])continue;
++sumn[g[i][j]];
suml[g[i][j]]+=g[i][j];
}
for(int j=1;j<=m;++j){
sumn[j]+=sumn[j-1];
suml[j]+=suml[j-1];
}
for(int j=1;j<=i;++j){
int len=f[i+1][j],dis=i+1-j;
ll L=max(1,dis-len),R=dis-flag;
if(L>R||R>m)continue;
ans+=suml[R]-suml[L-1]-(sumn[R]-sumn[L-1])*(L-1);
ans+=(sumn[m]-sumn[R])*(R-L+1);
}
}
}
int main(){
scanf("%s%s",s+1,t+1);
n=strlen(s+1),m=strlen(t+1);
solve(0);
for(int i=1;i<=n/2;++i)swap(s[i],s[n-i+1]);
for(int i=1;i<=m/2;++i)swap(t[i],t[m-i+1]);
swap(s,t);swap(n,m);
solve(1);
printf("%lld\n",ans);
return 0;
}