背包套路
最大分成两步骤:1.状态表示 2. 状态计算
1.状态表示
状态表示从两个角度来思考 :(1)集合 (2) 属性
(1)集合 : 满足某中条件下的所有选法的集合
(2)属性:最大值 / 最小值 / 数量
2.状态计算:
所谓状态计算就是集合的划分,满足两种原则:(1)不重 (2)不漏
对与求最大值和最小值的问题可以重复,但是求方案数量的时候不能重复
01背包
每件物品最多只能选一次(也可以不选)
思路:
状态表示: f[ i ] [ j ]
(1)集合:只从前i个物品当中选,并且总体积不超过 j 的所有选法
(2) 属性: 所有选法当中的最大价值(MAX)
状态计算:
(1) f[i - 1][j] : 不包含第 i 个物品的最大价值
(2) f[i - 1][j - v[i]] + w[i]: 包含第 i 个物品的最大价值
二维状态下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n,m;
int v[N],w[N];
int f[N][N];
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> v[i] >> w[i];
}
for(int i = 1; i <= n; i++){
for(int j = 0; j <= m; j++){
f[i][j] = f[i-1][j];
if(j >= v[i]) //还能装的下的情况下
f[i][j] = max(f[i][j],f[i-1][j-v[i]] + w[i]);
}
}
cout << f[n][m]; //前n个物品中,体积不超过m的最大价值
return 0;
}优化过程
for(int i = 1; i <= n; i++){
for(int j = v[i]; j <= m; j++){ //j是从小到大进行枚举的
f[j] = max(f[j], f[j - v[i]] + w[i]);
//在这一步骤当中,j - v[i] 是严格小于 j 的,
//因此枚举到j 之前j - v[i] 会被先更新掉,
//这样会影响后续的答案
//相当于 f[i][j] = max(f[i][j],f[i][j-v[i]] + w[i]),这个方程与原来的方程不一样
}
}
-------------------------------------------------------
//解决方法: 我们只要把 j 从大到小枚举即可
for(int i = 1; i <= n; i++){
for(int j = m; j >= v[i]; j--){
f[j] = max(f[j],f[j - v[i]] + w[i]);
}
}一维状态下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n,m;
int v[N],w[N];
int f[N];
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> v[i] >> w[i];
}
for(int i = 1; i <= n; i++){
for(int j = m; j >= v[i]; j--){
f[j] = max(f[j],f[j - v[i]] + w[i]);
}
}
cout << f[m] << endl;
return 0;
}完全背包
每件物品可以选无限次
思路:
朴素做法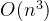
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int n,m;
int v[N],w[N];
int f[N][N];
int main(){
cin >> n >> m;
for(int i = 1; i <= n; i ++){
cin >> v[i] >> w[i];
}
for(int i = 1; i <= n; i++){
for(int j = 0; j <= m; j++){
for(int k = 0; k *v[i] <= j ; k++){
f[i][j] = max(f[i][j],f[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
cout << f[n][m] << endl;
return 0;
}方程的优化过程:

二维状态下进行优化:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++){
for(int j = 0; j <= m; j++){
f[i][j] = f[i - 1][j];
if(j >= v[i])
f[i][j] = max(f[i][j],f[i][j - v[i]] + w[i]);
}
}
cout << f[n][m] << endl;
return 0;
}
优化过程:
01背包: f[i][j] = max(f[i - 1][j] , f[i - 1][j] - v[i]] + w[i]);
完全背包:f[i][j] = max(f[i - 1][j] , f[i][j -v[i]] + w[i]);
经过观察,我们很容易看出完全背包与01 背包的差距在于,f[i][j - v[i]] + w[i] 这一部分。
这就刚好于上面分析过的 01背包相反,完全背包恰好用到的是同一层,因此 j 从小到大枚举即可
一维状态下:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++){
for(int j = v[i]; j <= m; j++){
f[j] = max(f[j],f[j - v[i]] + w[i]);
}
}
cout << f[m] << endl;
return 0;
}