数学
欧拉函数 : \(\phi(p)\) = 所有小于p且与p互质的数的个数
狭义积性: \(φ(ab)=\phi(a)\phi(b) (a,b互质时)\)
积性的证明:
令n = \(\prod p_i^{c_i}\)
则\(\phi(n)\) = n * $\prod \frac{p_i-1}{p_i} $ //prod中每一项表示因数\(p_i\)不出现的频率
"ab = n并且a,b互质" 可以转化成 "把一部分因数\(p_i^{c_i}\)分给a,另一部分分给b."
所以等式成立,证毕。
原根
define 原根g: \(g^i mod p \neq g^j mod p\) (p为素数)\
其中\(i \neq j\)且i, j介於1至(p-1)之间
简单的来说,如果g是P的原根,那么g的(1...P-1)次幂mod P的结果一定互不相同。
重要定理:\(g^{(P-1)}\) = 1 (mod P) (P为素数)
容斥原理
用于不重不漏地【表达/转化】某集合

二项式反演
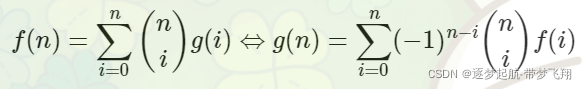
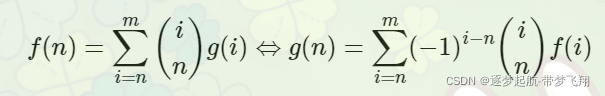
例:例题
斯特林数
define {n,m}:
将n个数放在m个非空集合的方案数
简单递推式:{\(_{n}^{m}\)} = {\(_{n - 1}^{m - 1}\)} + m * {\(_{n - 1}^ m\)}
递推边界:s(n, n) = 1(n >= 0), s(n, 0) = 0 (n > 0);
通项公式:\(s(n,m) = \sum_{i=0}^x\frac{i^n\cdot(-1)^{x-i}}{(x-i)!i!}\) (可用二项式反演得)
重要推论:$ x^n $ = \(\sum_{i=0}^{x}\){n,i}\(x\choose i\)i!
多项式
由牛顿迭代导出来的高级东西
\(F(x)\equiv F_k(x)-\frac{G(F_k(x))}{G'(F_k(x))}\pmod{x^{2n}}\)。