正文
纹理是物体表面固有的一种特性,所以图像中的区域常体现出纹理性质。纹理可以认为是灰度(颜色)在空间以一定的形式变化而产生的团(模式)。纹理与尺度有密切的关系,一般仅在一定的尺度上可以观察到,对纹理的分析需要在恰当的尺度上进行。纹理还具有区域性质的特点,通常被看做对局部区域中像素之间关系的一种度量,对于单个像素来说讨论纹理是没有意义的。一把情况下目前常用的纹理分析方法中有以下三种:统计法,结构法,频谱法。
1. 纹理描述的统计方法
最简单的统计法借助于灰度直方图的矩来描述纹理,比如直方图的二阶矩是灰度对比度的度量,可以用于描述直方图的相对平滑程度;三阶矩表示了直方图的偏度;四阶矩表示的直方图的相对平坦型等等。但是仅借助灰度直方图的矩来描述纹理没能利用像素相对位置的空间信息,为了利用这些信息,我们可以建立区域的灰度共生矩阵。
1.1 灰度共生矩阵
设 S 为目标区域 R 中具有特定空间联系(可由位置算子确定)的象素对的集合,共生矩阵 P 中的元素( #代表数量)
\(p\left(g_{1},g_{2}\right)=\frac{\#\{\left[\left(x_{1},y_{1}\right),\left(x_{2},y_{2}\right)\right]\in S|f\left(x_{1},y_{1}\right)=g_{1}\&f\left(x_{2},y_{2}\right)=g_{2}\}}{\#S}\)
分子:具有某种空间关系、灰度值分别为g1和g2的象素对的个数。分母:象素对的总和个数
上面提到了一个概念,位置算子,位置算子其实就是象素对的特定空间联系,比如向右1个象素和向下1个象素。共生矩阵的大小一般为k x k矩阵(k为所求图像的灰度级数)。举个例子如下:
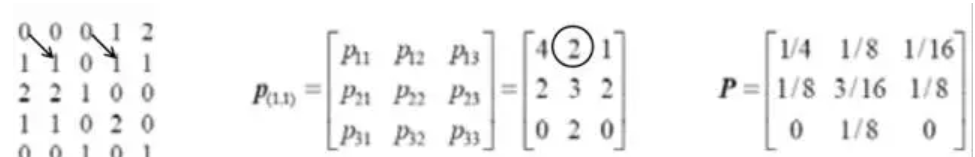
上图a为3个灰度级的图象( g1 = 0, g2 = 1, g3 = 2),位置算子为:向右1个象素和向下1个象素,b图按照位置算子计算得到的灰度共生矩阵,c图为共生矩阵归一化的结果。然而,为了更好的对图像分析,一般常用由共生矩阵产生的纹理描述符,比如:二阶矩,对应图像的均匀性或平滑性;熵,给出图像内容随机性的度量;对比度,反应紧邻像素间的反差等。