2024 CSP-J
P11227 扑克牌(模拟,STL)
题意
给定 \(n\) 张扑克牌,问若要凑齐所有花色点数,还需要几种牌。
数据规模与约定
对于 \(100\%\) 的数据,\(1 \le n\le 52\)。
题解
发现每种扑克牌是一个花色和点数的二元组。开一个二维数组当桶即可。
但是考虑到实现起来的方便性,这里我使用了枚举花色还有枚举点数求出所有的牌放到一个 set 中,然后不断 erase 掉。
#include<bits/stdc++.h>
using namespace std;
/*====================*/
#define endl '\n'
/*====================*/
using lnt = long long;
/*====================*/
void Solve(void)
{
int n; cin >> n;
string str1 = "DCHS";
string str2 = "A23456789TJQK";
set<string>lib;
for (auto c1 : str1)
{
for (auto c2 : str2)
{
string str;
str.push_back(c1);
str.push_back(c2);
lib.insert(str);
}
}
for (int i = 1; i <= n; ++i)
{
string str; cin >> str; lib.erase(str);
}
cout << lib.size() << endl;
}
/*====================*/
int main()
{
#ifndef ONLINE_JUDGE
freopen("IN.txt", "r+", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int T = 1; //cin >> T;
while (T--)Solve();
return 0;
}
P11228 地图探险(模拟)
题意
小 A 打算前往一片丛林去探险。丛林的地理环境十分复杂,为了防止迷路,他先派遣了一个机器人前去探路。
丛林的地图可以用一个 \(n\) 行 \(m\) 列的字符表来表示。我们将第 \(i\) 行第 \(j\) 列的位置的坐标记作 \((i, j)(1 \leq i \leq n, 1 \leq j \leq m)\)。如果这个位置的字符为 \(\tt x\),即代表这个位置上有障碍,不可通过。反之,若这个位置的字符为 \(\tt.\),即代表这个位置是一片空地,可以通过。
这个机器人的状态由位置和朝向两部分组成。其中位置由坐标 \((x, y)(1 \leq x \leq n, 1 \leq y \leq m)\) 刻画,它表示机器人处在地图上第 \(x\) 行第 \(y\) 列的位置。而朝向用一个 \(0 \sim 3\) 的 整数 \(d\) 表示,其中 \(d = 0\) 代表向东,\(d = 1\) 代表向南,\(d = 2\) 代表向西,\(d = 3\) 代表向北。
初始时,机器人的位置为 \((x_0, y_0)\),朝向为 \(d_0\)。保证初始时机器人所在的位置为空地。接下来机器人将要进行 \(k\) 次操作。每一步,机器人将按照如下的模式操作:
-
假设机器人当前处在的位置为 \((x, y)\),朝向为 \(d\)。则它的方向上的下一步的位置 \((x^′, y^′)\) 定义如下:若 \(d = 0\),则令 \((x^′, y^′) = (x, y + 1)\),若 \(d = 1\),则令 \((x^′, y^′) = (x + 1, y)\),若 \(d = 2\),则令 \((x^′, y^′) = (x, y - 1)\),若 \(d = 3\),则令 \((x^′, y^′) = (x − 1, y)\)。
-
接下来,机器人判断它下一步的位置是否在地图内,且是否为空地。具体地说,它判断 \((x^′, y^′)\) 是否满足 \(1 \leq x^′ \leq n, 1 \leq y^′ \leq m\),且 \((x^′, y^′)\) 位置上是空地。如果条件成立,则机器人会向前走一步。它新的位置变为 \((x^′, y^′)\),且朝向不变。如果条件不成立,则它会执行“向右转”操作。也就是说,令 \(d^′ = (d + 1) \bmod 4\)(即 \(d + 1\) 除以 \(4\) 的余数),且它所处的位置保持不变,但朝向由 \(d\) 变为 \(d^′\)。
小 A 想要知道,在机器人执行完 \(k\) 步操作之后,地图上所有被机器人经过的位置(包括起始位置)有几个。
数据规模与约定
对于所有测试数据,保证:\(1 \leq T \leq 5, 1 \leq n, m \leq 10^3\),\(1 \leq k \leq 10^6\),\(1 \leq x_0 \leq n\),\(1 \leq y_0 \leq m\),\(0 \leq d_0 \leq 3\),且机器人的起始位置为空地。
题解
注意到 \(k\) 的范围只有 \(10^6\),每次操作复杂度为 \(O(1)\),直接模拟即可。
#include<bits/stdc++.h>
using namespace std;
/*====================*/
#define endl '\n'
/*====================*/
using lnt = long long;
/*====================*/
const int N = 1e3 + 10;
const int M = 1e3 + 10;
const int K = 1e6 + 10;
/*====================*/
const int dx[] = { 0,+1,0,-1 };
const int dy[] = { +1,0,-1,0 };
/*====================*/
char mp[N][M];
bool vis[N][M];
/*====================*/
void Solve(void)
{
int ans = 0;
int n, m, k; cin >> n >> m >> k;
int x, y, d; cin >> x >> y >> d;
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
cin >> mp[i][j];
}
}
vis[x][y] = true; ans++;
while (k--)
{
int tx = x + dx[d];
int ty = y + dy[d];
bool flag = false;
if (1 <= tx && tx <= n)
{
if (1 <= ty && ty <= m)
{
if (mp[tx][ty] == '.')
{
flag = true;
if (vis[tx][ty] == false)
{
vis[tx][ty] = true; ans++;
}
x = tx, y = ty;
}
}
}
if (flag == false)d = (d + 1) % 4;
}
cout << ans << endl;
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
vis[i][j] = false;
}
}
}
/*====================*/
int main()
{
#ifndef ONLINE_JUDGE
freopen("IN.txt", "r+", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int T = 1; cin >> T;
while (T--)Solve();
return 0;
}
P11229 小木棍(打表找规律,贪心,数学归纳法,高精,dp)
题意
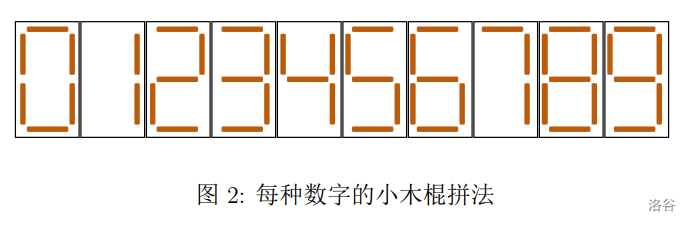
小 S 希望拼出一个正整数,满足如下条件:
- 拼出这个数恰好使用 \(n\) 根小木棍;
- 拼出的数没有前导 \(0\);
- 在满足以上两个条件的前提下,这个数尽可能小。
小 S 想知道这个数是多少,可 \(n\) 很大,把木棍整理清楚就把小 S 折腾坏了,所以你需要帮他解决这个问题。如果不存在正整数满足以上条件,你需要输出 \(-1\) 进行报告。
数据规模与约定
对于所有测试数据,保证:\(1 \leq T \leq 50\),\(1 \leq n \leq 10^5\)。
题解
直接看到这个题是很令人疑惑的。我们可以尝试打表寻找一下规律。打出表后,发现也找不到规律。我们看一下题面,看看是否能获得提示。发现无论是特殊性质 A 还是特殊性质 B,都跟 \(7\) 有关。对照一下打出的表发现,\(1-7\) 答案是一位数,\(8-14\) 答案是两位数,以此类推。
但是找不出规律来。我们继续看题面。发现性质 B 专门提到了一个 \(7k+1\)。我们令 \(7\) 个数为一组,观察下每一组的第一个数。发现开头都是 \(1\)。这启发我们继续观察。发现除 \(1-7\) 这一组以外,第一位数永远是 \(1,1,2,2,2,6,8\) 循环。继续观察后几位,找不出明显规律。
但是我们发现,从 \(15-21\) 这一组往后,只是不断地在后面添加数字 \(8\),前 \(3\) 位没有发生变化。
于是我们打表特判 \(n \le 21\) 的答案。对于 \(n > 21\) 的部分,判断一下距离 \(15-21\) 这一组有多远,然后在后面输出 \(8\) 即可。
关于这题为什么是这种规律:考虑到,我们肯定希望前缀是最小的。如果增加一根木棍,要在前缀修改和在后缀修改,肯定选择后缀。所以从 \(15-21\) 这一组往后,前缀不变了。其中数字 \(8\) 是所有数字中使用小木棍最多的数字,一共需要 \(7\) 根,能很好的消耗小木棍的数量。所以按模 \(7\) 进行讨论,往后不断填充数字 \(8\)。
这题使用高精 + dp 也可以进行求解。
#include<bits/stdc++.h>
using namespace std;
/*====================*/
#define endl '\n'
/*====================*/
using lnt = long long;
/*====================*/
const int NUM[] = { 6,2,5,5,4,5,6,3,7,6 };
/*====================*/
int ans[22];
void Init(void)
{
ans[1] = -1;
ans[2] = 1;
ans[3] = 7;
ans[4] = 4;
ans[5] = 2;
ans[6] = 6;
ans[7] = 8;
ans[8] = 10;
ans[9] = 18;
ans[10] = 22;
ans[11] = 20;
ans[12] = 28;
ans[13] = 68;
ans[14] = 88;
ans[15] = 108;
ans[16] = 188;
ans[17] = 200;
ans[18] = 208;
ans[19] = 288;
ans[20] = 688;
ans[21] = 888;
}
/*====================*/
void Solve(void)
{
int n; cin >> n;
if (n <= 21)
{
cout << ans[n] << endl;
}
else
{
int base = 14 + n % 7;
int k = (n - base) / 7;
cout << ans[base];
for (int i = 1; i <= k; ++i)cout << 8;
cout << endl;
}
}
/*====================*/
int main()
{
#ifndef ONLINE_JUDGE
freopen("IN.txt", "r+", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
Init();
int T = 1; cin >> T;
while (T--)Solve();
return 0;
}
P11230 接龙(图论,模拟,暴力,BFS)
题意
在玩惯了成语接龙之后,小 J 和他的朋友们发明了一个新的接龙规则。
总共有 \(n\) 个人参与这个接龙游戏,第 \(i\) 个人会获得一个整数序列 \(S_i\) 作为他的词库。
一次游戏分为若干轮,每一轮规则如下:
- \(n\) 个人中的某个人 \(p\) 带着他的词库 \(S_p\) 进行接龙。若这不是游戏的第一轮,那么这一轮进行接龙的人不能与上一轮相同,但可以与上上轮或更往前的轮相同。
- 接龙的人选择一个长度在 \([2, k]\) 的 \(S_p\) 的连续子序列 \(A\) 作为这一轮的接龙序列,其中 \(k\) 是给定的常数。若这是游戏的第一轮,那么 \(A\) 需要以元素 \(1\) 开头,否则 \(A\) 需要以上一轮的接龙序列的最后一个元素开头。
- 序列 \(A\) 是序列 \(S\) 的连续子序列当且仅当可以通过删除 \(S\) 的开头和结尾的若干元素(可以不删除)得到 \(A\)。
为了强调合作,小 J 给了 \(n\) 个参与游戏的人 \(q\) 个任务,第 \(j\) 个任务需要这 \(n\) 个人进行一次游戏,在这次游戏里进行恰好 \(r_j\) 轮接龙,且最后一轮的接龙序列的最后一个元素恰好为 \(c_j\)。为了保证任务的可行性,小 J 请来你判断这 \(q\) 个任务是否可以完成的,即是否存在一个可能的游戏过程满足任务条件。
数据规模与约定
对于 \(100\%\) 的数据:
- \(1 \leq T \leq 5\);
- \(1 \leq n \leq 10^5\),\(2 \leq k \leq 2 \times 10^5\),\(1 \leq q \leq 10^5\);
- \(1 \leq l_i \leq 2 \times 10^5\),\(1 \leq S_{i,j} \leq 2 \times 10^5\);
- \(1 \leq r_j \leq 10^2\),\(1 \leq c_j \leq 2 \times 10^5\);
- 设 \(\sum l\) 为单组测试数据内所有 \(l_i\) 的和,则 \(\sum l\leq 2\times 10^5\)。
题解
首先发现 \(q\) 个询问可以预处理完统一回答。
看到接龙问题,本能往图论建模的方向思考。我们可以假设某个开头往某个结尾连边来建图。对这张图 BFS 暴力,判断 BFS 的每一层都有哪些单词可以作为结尾就可以。
这里存在两个问题,首先我们发现边的数量太多,其次我们没办法区分上一轮和这一轮是不是同一个人。为了区分是否为同一个人,我们要建分层图,边的数量更多了。所以乍一看这条路走不通。
看一下暴力怎么做。我们每一轮,枚举每一个人的每一个子串。发现轮数很少,只有 \(1e2\)。但是后面枚举所有人的所有子串复杂度太高了,考虑优化。
我们发现,对于一个子串 \(s\),假设开头为 \(A\),结尾为 \(T\)。我们并不在乎 \(<A,T>\) 必须要绑定起来。我们只在乎上一轮作为结尾的 \(A\),和这一轮作为开头的 \(A\),不是同一个人,且这个子串长度在 \([2,k]\) 之间。所以子串数从平分级变成了一次方级。
那问题就只剩下,如何判断 \(A\) 是否作为上一轮的某个结尾,和如何判断上一轮和这一轮不是同一个人。
我们可以开一个集合 set,\(tag[turn][c]\) 数组来记录一下,表示第 \(turn\) 轮,以 \(c\) 结尾,都有哪些人。
这样我们只需要每一轮,枚举每一个人的每一个数字,记录一下第 \(i\) 人有哪些下标可以作为开头。只需要 !tag[turn-1][c].empty() && (tag[turn-1][c].size()>=2 || *tag[turn-1][c].begin()!=i)。先保证上一轮这个结尾存在,如果有多个人上一轮是这个结尾,那随便,如果只有一个人,要判断不是自己。
然后我们发现,没必要开一个 set。只需要一个变量记录即可。用 \(-1\) 表示结尾不合法,用 \(i\) 表示结尾是第 \(i\) 个人的,用 \(0\) 表示有多个人。
记录下来第 \(i\) 个人的所有可以作为开头的下标后,再扫描一遍,钦定当前下标 \(j\) 可以作为结尾。那就需要满足存在一个开头,使得距离在 \([2,k]\) 之间。对于刚刚的记录我们只需要解一下不等式,求出开头的下标区间,然后 lower_bound 去判断一下即可。
然后我们发现,我们只关注距离结尾最近的开头即可。所以也没必要记录所有开头的下标,也不需要 lower_bound。用一个变量存一下即可。
总时间复杂度 \(O(r n+r\sum l+q)\)。
#include<bits/stdc++.h>
using namespace std;
/*====================*/
#define endl '\n'
/*====================*/
using lnt = long long;
/*====================*/
const int N = 1e5 + 10;
const int R = 1e2 + 10;
const int C = 2e5 + 10;
/*====================*/
const int INF = 0X3F3F3F3F;
/*====================*/
int n, k, q;
vector<int>s[N];
int tag[R][C];//记录第r层,c结尾,是谁接龙的。
/*====================*/
void Insert(int r, int c, int id)
{
if (tag[r][c] == -1)
{
tag[r][c] = id;
}
else if (tag[r][c] != id)
{
tag[r][c] = 0;
}
}
/*====================*/
void Solve(void)
{
cin >> n >> k >> q;
for (int i = 1; i <= n; ++i)
{
int l; cin >> l; s[i].assign(l, 0);
for (int j = 0; j < l; ++j)cin >> s[i][j];
}
memset(tag, -1, sizeof(tag)); tag[0][1] = 0;
for (int turn = 1; turn <= 1e2; ++turn)
{
for (int i = 1; i <= n; ++i)
{
int head = -INF;
for (int j = 0; j < s[i].size(); ++j)
{
if (head >= j - k + 1)Insert(turn, s[i][j], i);
if (tag[turn - 1][s[i][j]] != -1 && tag[turn - 1][s[i][j]] != i)head = j;
}
}
}
for (int i = 1; i <= q; ++i)
{
int r, c; cin >> r >> c;
cout << (tag[r][c] == -1 ? 0 : 1) << endl;
}
}
/*====================*/
int main()
{
#ifndef ONLINE_JUDGE
freopen("IN.txt", "r+", stdin);
#endif
ios::sync_with_stdio(false);
cin.tie(NULL), cout.tie(NULL);
int T = 1; cin >> T;
while (T--)Solve();
return 0;
}