简介
定义:
- 欧拉回路:通过图中每条边恰好一次的回路
- 欧拉通路:通过图中每条边恰好一次的通路
- 欧拉图:具有欧拉回路的图
- 半欧拉图:具有欧拉通路但不具有欧拉回路的图
摘自: oi-wiki。
定义说白了就是小学的一笔画问题,这里直接给出三道例题。P7771 【模板】欧拉路径,CF508D 和 CF36E。
例题
P7771 【模板】欧拉路径
思路
模板题,没有思路。直接讲一下求欧拉路径的方法即可。
首先,对于一个图,它要存在欧拉路径的必要条件很简单。就是奇点的个数要为 0 或者 2。其他情况都是无解的。这两种情况对应的图的形态长这样捏:
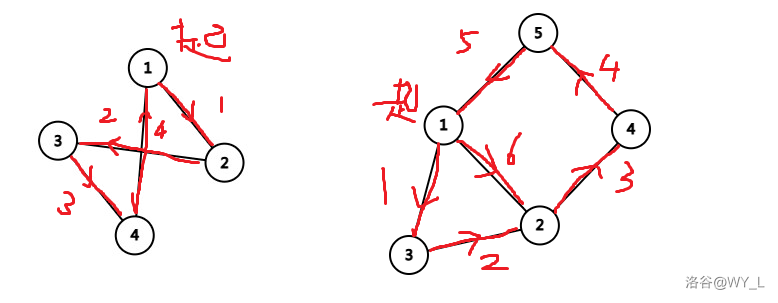
当然这也不是唯一解。其中第一个图中没有奇点,而第二个图中奇点为 1 和 2。
这里给出求解欧拉路径的伪代码:
void dfs(int u){
遍历u的所有出边
如果该边还存在
删掉这条边
dfs(该边去往的点)
u入栈
}
这里给出一点 luogu 的大部分题解都没有解释到的地方。为什么不能遍历到一个点就将该点入栈,非要循环结束后才可以?这里举出一个例子:如果有一个无向图长得像一个 8 字,就像下面这样:
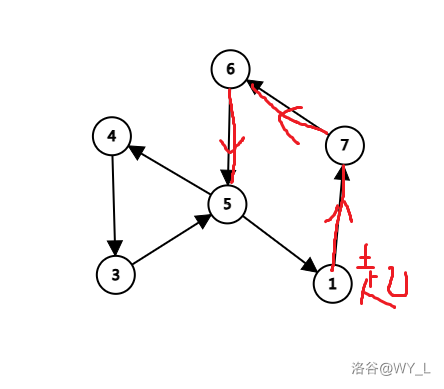
当我们走到 5 的时候会发生一个事情。就是说这个时候我们既可以选择往 1 走也可以往 4 走。我们希望的是向 4 走。如果我们最后再入栈那么当它 dfs 到 1 的时候就只会推掉 5 和 1 之间的部分,再从 5 开始继续搜索。相当于我们最开始的 \([1,7,6,5]\) 加上 \([5,4,3,5]\) 以及 \([5,1]\) 就是我们最后的答案。这里需要倒序输出,这里借鉴了 Marsrayd 大佬的 博客。这里是这样说的:
感性理解倒序输出的原因:如果是欧拉回路,那么遍历到哪,输出到哪也是对的,因为不管怎么走都会绕某个环走回起点,所以不到最后不会出栈,然而欧拉路径会出现边都被走过了,走不回起点,最后会停留在终点,遇到这种情况这种路径会最先出栈,于是只要把这个路径先走了,前面就和欧拉回路一样随便走就行,不会出栈,于是倒序输出就是对的
膜拜大佬。这个说得非常清楚啊。
CF508D
思路
此题很板啊。我们直接把这个字符串的前面的两个字符和后面的两个字符各看作一个点,连一条单向边。因为这题要求相同的字符串之间连线。那么我们把它转成 int 了之后就自然而然连上边了。
我们需要再记录一个每个点的出度和入度。来判断改图是否存在欧拉路径。
其实就是一个板题,这边给出可爱的代码:
AC code
点击查看代码
#include<bits/stdc++.h>
using namespace std;
namespace WYL{
const int N=3e5+10;
const int INF=2e5;
vector<int> edge[N];
vector<int> point;
int n,outde[N],inde[N],Start;
string ans;
void dfs(int u){
while(!edge[u].empty()){
int to=edge[u][edge[u].size()-1];
edge[u].pop_back();
dfs(to);
}
ans+=(char)(u%256);
}
int main(){
cin>>n;
memset(outde,0,sizeof(outde));
memset(inde,0,sizeof(inde));
string s;
for(int i=1;i<=n;i++){
cin>>s;
int u=s[0]*256+s[1],v=s[1]*256+s[2];
edge[u].push_back(v);
outde[u]++;
inde[v]++;
Start=u;
}
int k=3e5;
for(int i=0;i<=k;i++){
if(edge[i].size()!=0){
point.push_back(i);
}
}
if(n==1){
cout<<"YES"<<endl;
cout<<s<<endl;
return 0;
}
int flag=0,cnt=0;
for(int i=0;i<=INF;i++){
if(outde[i]!=inde[i]){
flag=1;
}
if(abs(outde[i]-inde[i])==1){
cnt++;
}
if(abs(outde[i]-inde[i])>1&&outde[i]!=inde[i]){
cout<<"NO"<<endl;
return 0;
}
if(outde[i]-inde[i]==1){
Start=i;
}
}
if(flag==1&&cnt!=2){
cout<<"NO"<<endl;
return 0;
}
dfs(Start);
ans+=Start/256;
if(ans.size()<n+2){
cout<<"NO"<<endl;
return 0;
}
cout<<"YES"<<endl;
reverse(ans.begin(),ans.end());
cout<<ans<<endl;
return 0;
}
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
WYL::main();
return 0;
}
CF36E
写在前面的话
也许是本人太蒟了。本人认为本题的代码难度远高于 CF508D,但是 CF 的评分只差了 100 分(喜。
题意
翻译说得很清楚,这里再重复一下。
给你一张无向图,不保证连通以及可能有重边。让你求两条路径,使其正好能够覆盖所有的边,按边的编号输出答案。
思路
首先。这道题与 CF508D 的不同点在于这道题要求的是两条路径。于是我们尝试分类讨论。
因为不保证连通。我们首先知道,如果连通块的数量是 1 或者 2 的时候都有解。为什么?这个很显然,如果有大于两个的连通块。那么一定不存在两条路径能够覆盖掉所有的点。于是连通块数量大于 2 时我们可以直接把这个图 ban 掉。
好的现在我们来看连通块为 1 的情况。因为我们要求的路径相当于就是一个欧拉路径。所以在连通块为 1 的情况下度数为奇数的个数就只可能是 0,2 或者 4。其中呢 0 和 2 都比较好处理。只要当路径长度比 2 大就一定可以分成两坨。但是呢 4 就需要想一想了。这里提供一种蒟蒻的想法:我们找到两个没有连边的奇点将它们之间连上一条虚边(不是重链剖分里的那个捏)。跑一遍欧拉路径,然后再把那条虚边给删掉。得到的两个部分就是我们所求的,这里给出一个例子:
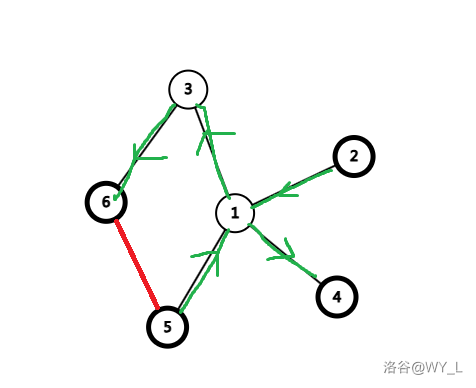
输入数据:
5
1 2
1 4
1 3
1 5
3 6
这里我连上了 5 与 6 之间的边。再删掉再删掉红色的边,就得到了点集为 \([1,4,5]\) 与 \([1,2,3,6]\) 的答案。
连通块为 1 的情况看完了。现在来研究连通块数量为 2 的。显然只有在两个连通块的奇点个数都为 0 或者都为 2 时才是有解的。如果有解直接各找一个欧拉路径就可以啦。
AC code
点击查看代码
#include<bits/stdc++.h>
using namespace std;
namespace WYL{
const int N=1e5+10;
int n,to[N],nxt[N],head[N],tot,du[N],kid[N],kcnt,kminn[N];
bool mark[N],vis[N];
vector<int> jidian,path,jidian1,jidian2,path1,path2;
void add(int u,int v){
nxt[++tot]=head[u];
head[u]=tot;
to[tot]=v;
return;
}
void dfs(int id,int k){
kid[id]=k;
for(int i=head[id];i;i=nxt[i]){
if(kid[to[i]]==0&&du[to[i]]!=0){
dfs(to[i],k);
}
}
return;
}
int find_edge(int x,int y){
for(int i=head[x];i;i=nxt[i]){
if(to[i]==y&&!mark[(i+1)/2]){
return i;
}
}
return -1;
}
void Euler(int u,vector<int> &tmp){
if(du[u]==0){
tmp.push_back(u);
return;
}
for(int i=head[u];i;i=nxt[i]){
// cout<<u<<"->"<<to[i]<<endl;
if(vis[(i+1)/2]){
continue;
}
vis[(i+1)/2]=true;
du[to[i]]--;
du[u]--;
// cout<<"***"<<u<<"->"<<to[i]<<endl;
Euler(to[i],tmp);
}
tmp.push_back(u);
return;
}
void solve(int l,int r,vector<int> path){
for(int i=l;i<=r;i++){
int opt=(find_edge(path[i],path[i+1])+1)/2;
cout<<opt<<" ";
mark[opt]=true;
}
return;
}
int main(){
cin>>n;
if(n==1){
cout<<"-1"<<endl;
return 0;
}
for(int i=1;i<=n;i++){
int x,y;
cin>>x>>y;
du[x]++;
du[y]++;
add(x,y);
add(y,x);
}
for(int i=1;i<=10005;i++){
if(du[i]&&kid[i]==0){
kminn[kcnt+1]=i;
dfs(i,++kcnt);
}
if(du[i]%2==1){
jidian.push_back(i);
}
}
if(kcnt>2){
cout<<"-1"<<endl;
return 0;
}
if(kcnt==1){
if(jidian.size()==4){
for(int i=0;i<4;i++){
for(int j=i+1;j<4;j++){
if(find_edge(jidian[i],jidian[j])!=-1){
continue;
}
swap(jidian[0],jidian[i]);
swap(jidian[1],jidian[j]);
goto end;
}
}
end:
int x=jidian[0],y=jidian[1];
du[x]++;
du[y]++;
add(x,y);
add(y,x);
memset(vis,0,sizeof(vis));
Euler(jidian[2],path);
int place=0;
while((path[place]!=jidian[0]||path[place+1]!=jidian[1])&&(path[place]!=jidian[1]||path[place+1]!=jidian[0])){
place++;
}
cout<<place<<endl;
solve(0,place-1,path);
cout<<endl;
cout<<n-place<<endl;
solve(place+1,path.size()-2,path);
return 0;
}else{
path.clear();
if(jidian.size()!=0&&jidian.size()!=2){
cout<<"-1"<<endl;
return 0;
}
if(jidian.size()==0){
Euler(kminn[1],path);
}else if(jidian.size()==2){
Euler(jidian[0],path);
}
cout<<"1"<<endl;
solve(0,0,path);
cout<<endl;
cout<<path.size()-2<<endl;
solve(1,path.size()-2,path);
return 0;
}
}else if(kcnt==2){
for(int i=0;i<jidian.size();i++){
if(kid[jidian[i]]==1){
jidian1.push_back(jidian[i]);
}else{
jidian2.push_back(jidian[i]);
}
}
if(jidian1.size()!=0&&jidian1.size()!=2){
cout<<"-1"<<endl;
return 0;
}
if(jidian2.size()!=0&&jidian2.size()!=2){
cout<<"-1"<<endl;
return 0;
}
path1.clear();path2.clear();
if(jidian1.size()==0){
int place=1;
while(kid[place]!=1){
place++;
}
Euler(place,path1);
}else{
Euler(jidian1[0],path1);
}
cout<<path1.size()-1<<endl;
solve(0,path1.size()-2,path1);
cout<<endl;
if(jidian2.size()==0){
int place=1;
while(kid[place]!=2){
place++;
}
Euler(place,path2);
}else{
Euler(jidian2[0],path2);
}
cout<<path2.size()-1<<endl;
solve(0,path2.size()-2,path2);
return 0;
}
return 0;
}
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
WYL::main();
return 0;
}
/*
10
7 4
7 4
6 1
2 3
2 1
1 6
4 2
8 4
4 8
3 5
*/