平面图最短路与对偶图网络流

一个相当厉害的东西啊。

参考原件：IOI 2008 国家集训队论文——周冬。

图片引自

1. OI-wiki 平面图
2. llmmkk ’s blog
3. 论文原件

先给出结论：

平面图最小割等于其对偶图最短路

平面图

平面图，指可以通过画图方式将使得边两两不相交的图。(无向图)

例如：

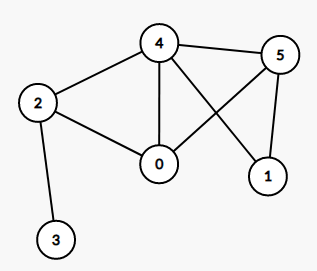
事实上是：

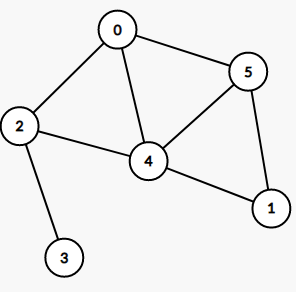
一些概念：

• 设 \(G\) 是平面图，由 \(G\) 的边将 所在的平面划分成若干个区域，每个区域称为 \(G\) 的一个面，其中面积无限的面称为无界面或外部面，面积有限的称为有限面或内部面。包围每个面的所有边组成的回路称为该面的边界，边界的长度称为该面的次数(边数)。显然有次数之和为 \(2|E|\)

• 阶数 也就是 \(|V|\)，边数也就是 \(|E|\)。

• 若在简单平面图 \(G\) 的任意不相邻顶点间添加边，所得图为非平面图，称 \(G\) 为极大平面图。

  一个 \(||\)

• 一个 \(|V|=5\) 的完全图不是平面图，一个 \(|L|=|R|=3\) 的完全二分图不是平面图。

  一个图是平面图当且仅当不存在可以收缩到上述两种情况的子图

• 典型的平面图是网格图。

• \(|V|-|E|+C=2\)，其中 \(C\) 是面数，欧拉公式，以下也采用 \(|V|,|E|,C\) 表示阶数边数面数。

• S-T 平面图：图中的一个点为源点 \(s\)，另外一个点为汇点 \(t\)，且 \(s\) 和 \(t\) 都在图中的无界面的边界上

对偶图

平面图的对偶图也是一个平面图，具体构造方法如下：

1. 将每个面视作一个点

   

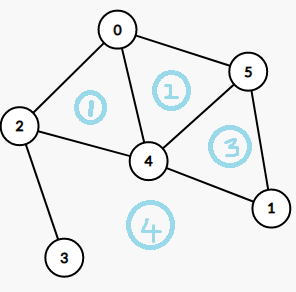
2. 按照如下方法构造：

   \(\forall (u,v,w)\in E\)

   1. 该边同时属于面 \(f_1,f_2\)，则连边 \((f_1,f_2,w)\)
   2. 该边仅属于面 \(f\)，则连边 \((f,f,w)\)。也即自环。
   3. 注意都是无向边

   

   

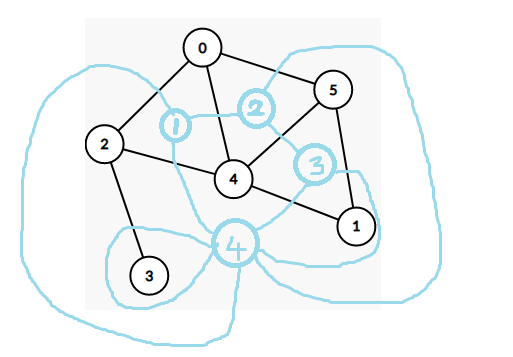
性质：

• 对偶图的每一个环对应原图的一个割（一一对应）
• 对偶图与原图边数相同，对偶图点数等于原图面数，可得对偶图面数等于原图点数

建立对偶图与 S-T 平面图关系

容易想到一种构造方法：

• 连接 \(S-T\)，边权为零，得到一个附加面，对这样的一个平面图建立对偶图

  

• 称原本附加面对应点为 \(s^*\)，原本无界面对应点为 \(t^*\)

  

• 我们让新图的边权等价为容量，则我们所求 \(s\to t\) 的最小割等价于该图包含 \(s^*,t^*\) 的一个边权和最小的环，由于 \(s^*,t^*\) 之间边权为零，因此这个边权和等价于删去 \((s^*,t^*)\) 后 \(s^*\to t^*\) 的最短路。

• 我们使用 Dijkstra 算法求解最短路即可，复杂度得到大大降低。

实际应用

实际应用中这个平面图常常抽象为网格图，从 \((0,0)\to (n,m)\)。

然后上右两个边界连向 \(S^*\)，下左两个边界连向 \(T^*\)，不过由于对称性反过来也没什么。

正向：CSP-S2021 交通规划

简要题意：给定一张网格图，每次给出 \(k\) 个边界上的交点作为关键点，每个点有颜色（黑白两色之一），你需要将非关键点染为黑白两色，使得 \(\sum_{(u,v,w),col_u\neq col_v}w\) 最小。求出这个最小值。

容易发现题目即为求解一个割掉边的方案使得所有黑色关键点与白色关键点不连通且割的边边权和最小。

很容易想到暴力网络流建图，可以获得 65 pts。

然后考虑 \(k=2\) 的部分分，此时 \(s,t\) 确定，可以利用转对偶图的方法通过。

两者综合可以获得相当可观的分数。

当一般 \(k\) 的时候，直接建立超级原点和超级汇点再转对偶图是错误的，它不一定是一个平面图（因为都在无界面上，而且可能黑白点有交叉，这就是非平面图了）。

但是我们受到了一些启发，我们将相邻的同色特殊点合并在一起，然后将合并后两个相邻非同色特殊点的部分依次划分为 \(s_i,t_i\)（也即 \(0\to 1:s\)，\(1\to 0:t\)），则显然最优方案一定是非同色块的两两配对（分类讨论即可证明），割掉这两个块之间的最短路即可。

我们可以 \(O(nmk\log nm)\) 地跑最短路求出各个块两两间的最短路，也就是割掉的代价，那么问题转化为：有一个长度为 \(2n\) 的环，环上 \(i,j\) 连边的代价为 \(d_{i,j}\)，你需要对于每个奇数点与偶数点匹配（两两匹配），要求线段不交（相交定然不优），求最小匹配代价。

这个套路很多，可以将其视作括号序列等，利用破环为链后的区间DP可以轻松求解。

\(f_{l,r}=\min(f_{l+1,r-1}+d_{l,r},f_{l,k}+f_{k+1,r})\)

最终复杂度 \(O(nm(\sum k)\log nm+\sum k^3)\)

反向：某模拟赛题

给定一张网格图，边有边权，你可以花费 \(1\) 将一条边的边权增加 \(1\)，求出最小的花费 \(w\)，使得第一行的点到最后一行的点的最短路（多源对多汇）增加 \(k\)。

建立对偶图，相当于每次花费 \(1\) 的代价扩展容量，则可以连接一条容量 \(inf\)，代价 \(1\) 的副边跑流量为 \(d+k\)，其中 \(d\) 是最短路长度的最小费用流即可（这里可以限制 \(S\) 的流量，也可以建立 \(S'\) 作为新的 \(S\) 连接到 \(S\) 的边容量 \(d+k\)）。

复杂度玄学。