前言
\(\text{K-D Tree (K-Dimension Tree)}\) 是一种可以有效处理高维信息的数据结构。
在一般信息学竞赛题目中 \(k = 2\),此时它又称 \(\text{2-D Tree}\)。
但遗憾的是,\(k \ge 3\) 的情况并不常见,这个我们后面再说明原因。
算法描述
问题
首先从简单的情况考虑起,假设信息只有一维,那我们通常用线段树维护,这样对于任意区间 \([l, r]\),我们可以将其表达为若干子区间的并。
但是现在信息变成了 \(k\) 维,直接线段树肯定是不行的。于是我们考虑类似线段树的,对于 \(k\) 维空间进行划分,将任意一个超立方体表示为划分出的若干子空间的不交并。
不过上述问题过于困难,没有什么有效解法。于是考虑一个弱化版:
- 给定 \(k\) 维空间中的 \(n\) 个点,每次给出一个超立方体,将被这个超立方体包含的点集,用较少的结点数表示。
这就是 \(\text{K-D Tree}\) 需要解决的抽象化问题。这里是一道模板题,可能题面中对 \(\text{K-D Tree}\) 性质的刻画并不全面,导致有一些奇奇怪怪的莫队可以通过,不过这部重要,大家拿去测测 \(\text{K-D Tree}\) 就好。
有人可能会问了:不就是多了几维,写个树套树上去不就是 \(\text{poly}(\log n)\) 的吗?
但显然并不是所有高维问题树套树都适用,树套树的本质是将两个维度分离,而不是 \(\text{K-D Tree}\) 所使用的整体解决,这样的结构会有如下缺陷:
-
不能支持修改。因为你的第一层树(假设是线段树)会将原本信息拆分成 \(O(\log n)\) 份,每次在第一棵树上修改时只能定位到其中一份,所以树套树时不支持修改的。
-
无法处理一些特殊问题。比如说线段树的结构支持线段树二分,线段树分治,甚至是单侧递归等等。这些显然在二维线段树上不支持,而 \(\text{K-D Tree}\) 是支持的。
前置讨论:Leafy or Nodey?
我们知道树形结构是非常优美的,很多数据结构本质上都是一棵树(即使是序列分块也可以看作这样)。
但这些数据结构维护信息的方式不完全相同:比如线段树只有叶子结点存储了原信息,其他结点存储的是若干叶子结点信息的并;而平衡树则不同,每个结点既合并了它所有后代的信息,又加入了自己的信息。
对于类似线段树这样的只有叶子处存储原信息的数据结构,我们称它是 \(\text{Leafy}\) 的。
而对于平衡树这样的在每个结点处都存储一份原信息的数据结构,我们称它是 \(\text{Nodey}\) 的。
常见的 \(\text{Leafy}\) 数据结构就是线段树,以及线段树的各种变体。还有就是 \(\text{WBLT}\) 和 \(\text{Leafy Tree}\) 也是 \(\text{Leafy}\) 的,我都没写过,这里提一嘴就好。
而 \(\text{Nodey}\) 结构一般在平衡树中出现较多,\(\text{OI}\) 界最常见的 \(\text{Treap}\) 和 \(\text{Splay}\) 就是 \(\text{Nodey}\) 的。原因很好理解:平衡树要支持动态插入删除,\(\text{Leafy}\) 结构不好维护它。
问题来了,\(\text{K-D Tree}\) 是 \(\text{Leafy}\) 的还是 \(\text{Nodey}\) 的呢?
其实是两种都可以的,并且都有人写。我个人倾向于认为将 \(\text{K-D Tree}\) 写成 \(\text{Leafy}\) 的更好,原因是:
-
显然 \(\text{Leafy}\) 比 \(\text{Nodey}\) 更好写,因为 \(\text{Leafy}\) 是二分结构,而 \(\text{Nodey}\) 相当于三分结构。一般情况下也是 \(\text{Leafy}\) 的数据结构常数较小。
-
后面我们要谈的 \(\text{K-D Tree}\) 分治,必须要用到 \(\text{Leafy}\) 结构。不难发现 \(\text{Nodey}\) 结构天然是无法(或者说很难,因为你当然可以每个结点下面加一个叶子强制变成 \(\text{Leafy}\) 结构,再线段树分治,那又何必呢?)支持线段树分治的。
-
\(\text{K-D Tree}\) 维护的很多都是离线问题,很少有要求动态插入删除还带强制在线的问题(不是说没有,是很少)。如果你看到了类似上面的情况,请你反思一下这道题有没有更好的,或者不用 \(\text{K-D Tree}\) 的做法。
于是我们主动舍弃 \(\text{Nodey}\) 结构带来的便于插入删除的优势,而选择将 \(\text{K-D Tree}\) 搭配上 \(\text{Leafy}\) 结构。
当然你要学 \(\text{Nodey}\) 的版本也是可以的,可以去隔壁 \(\text{OI-Wiki}\) 看看。不过即使你的 \(\text{K-D Tree}\) 一直就是 \(\text{Nodey}\) 的恐怕对后面的内容也没有太大影响。
算法流程
建树
现在考虑给出 \(k\) 维空间中的 \(n\) 个点,如何建出一棵树。
由于我们要快速定位一个超立方体,所以我们还是类似线段树的对于某一维度排序后划分为前后两半。
在线段树中我们不用考虑选择哪个维度,因为只有一个。但现在拓展到 \(k\) 维,我们必须做出选择。
容易想到我们交替划分,比如 \(k = 2\) 的情况,我们第一次对第 \(1\) 个维度进行划分,第 \(2\) 次对第 \(2\) 个维度进行划分,第 \(3\) 次又回到第 \(1\) 个维度,依次类推。
比如下图是 \(k = 2\) 的情况:
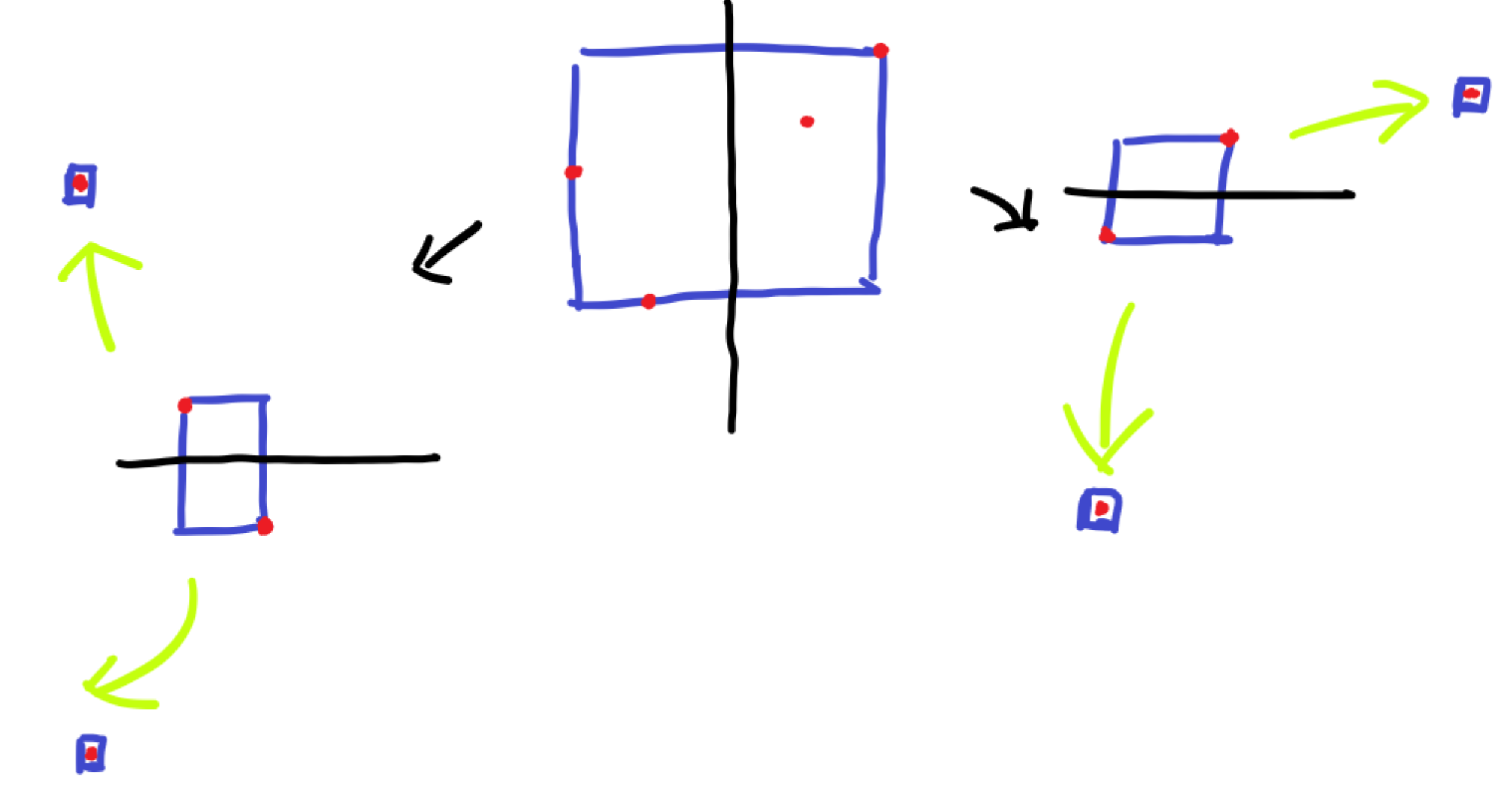
我们不断划分,直到点集中只有一个点,此时说明我们走到了一个叶子结点,可以直接返回。
一个实现细节是,我们相当于要找某一个维度中的前 \(k\) 小值,这个可以使用 \(\text{nth_element}\) 函数,时间复杂度为线性。
最后对于每个非叶子结点,记得维护点集中 \(k\) 维中每一维度的最大、最小坐标,后面需要用这个来加速查询。这个可以直接由两个儿子合并上来。
与一般线段树不同的是,\(\text{K-D Tree}\) 建树的时间复杂度为 \(O(n \log n)\),因为题目中给定的是点集,你需要对这个点集做类似排序的操作,所以带 \(\log\) 是无法避免的。
不过我们在后面将看到,比起查询和其他操作而言,建树的复杂度小的简直可以忽略不计。
查询
考虑我们要查询一个超立方体,并且我们当前在 \(\text{K-D Tree}\) 上某个结点 \(p\)。
我们发现此时没有什么好的方法,唯一能做的就是两件事:
- 若查询的超立方体包含了 \(p\) 代表点集中的所有点,则定位成功,直接返回 \(p\)(或者 \(p\) 处维护的一些信息)即可。
- 若查询的超立方体与 \(p\) 代表点集围成的最大超立方体相离,则 \(p\) 点集中所有点不可能在查询的超立方体中,所有我们直接 \(\text{return}\)。
以上两步都可以通过我们前面维护的子树内每一维度 \(\min/\max\) 快速处理。
如果上述两种情况都不满足,那我们也没有什么好的办法,递归两颗子树即可(显然如果是叶子必定落入前面两种情况中的一种)。
后面我们将证明,这样做访问和定位的结点数都是 \(O(n^{1 - \frac{1}{k}})\) 的。这里我们明确几个概念:
- 访问指查询时经过的结点总数。而定位指将超立方体中点集拆分到的结点,满足这些节点两两不交,且并起来是你查询的东西。
所以时间复杂度就是 \(O(n^{1 - \frac{1}{k}})\),当 \(k = 2\) 时我们将得到 \(O(\sqrt n)\)。
复杂度分析
回忆一下我们是如何证明线段树的时间复杂度的。我们发现若查询的是前缀或后缀,则我们只需单侧递归,时间复杂度 \(O(\log n)\)。
而任意区间怎么分析呢?考虑若查询的线段不包含中点,则只会单侧递归。若包含中点,则原区间会变成两个前缀或后缀。所以时间复杂度也是 \(O(\log n)\) 的。
考虑通过类似方式分析 \(\text{K-D Tree}\) 的时间复杂度。先考虑 \(k = 2\) 的情况,我们发现任意矩形的查询没有性质,于是我们尝试将它变成像前缀/后缀那样有性质的矩形。
对于任意矩形,它没有任意一维是前缀/后缀,我们称其为 \(\text{4-side}\) 矩形,考虑类似前面线段树的分析,将其拆为 \(O(1)\) 个 \(\text{2-side}\) 矩形。
接下来我们只分析 \(\text{2-side}\) 矩形的查询(假设是一个右下矩形),设 \(T(n)\) 为在 \(n\) 个结点的 \(\text{K-D Tree}\) 上查询的时间复杂度。考虑最坏情况形如下面两种:
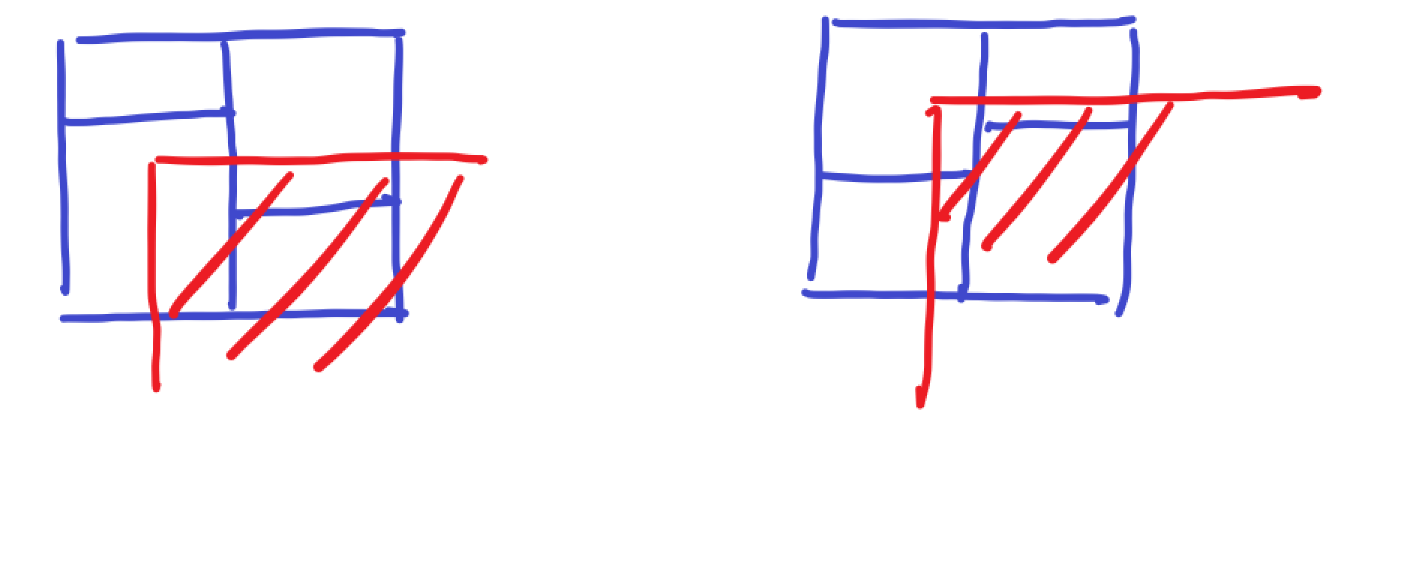
考虑第一种情况,右下的矩形被包含,左上的矩形不交,处理它们的时间复杂度为 \(O(1)\),而剩下两块仍然是 \(\text{2-side}\),则
\[T(n) = 2T(\frac{n}{4}) + O(1) \]由 Master 定理可得 \(T(n) = O(\sqrt n)\)。
第二种情况,右下的矩形完全被包含,左上的矩形是 \(\text{2-side}\),而剩余两个注意到它是 \(\text{1-side}\)(这样说可能不严谨,不过为方便理解就不改了),我们设处理 \(\text{1-side}\) 查询时间复杂度为 \(T_0(n)\)。
则
\[T(n) = T(\frac{n}{4}) + 2T_0(\frac{n}{4}) + O(1) \]考虑分析 \(T_0\),显然经过横向和竖向分割各一次后,最多剩下两个 \(\text{1-side}\) 矩形,于是
\[T_0(n) = 2T_0(\frac{n}{4}) + O(1) = O(\sqrt n) \]将 \(T_0\) 带回去,得到
\[T(n) = T(\frac{n}{4}) + O(\sqrt n) \]这个递归式用手画一画递归树,发现它也满足 \(T(n) = O(\sqrt n)\) 的。
这样我们就证明了 \(k = 2\) 时 \(\text{K-D Tree}\) 时间复杂度为 \(O(\sqrt n)\)。
对于 \(k \ge 3\) 的情况,由于很少用到,于是证明就略去了,结论是 \(T(n) = 2^{k - 1}T(\frac{n}{2^k}) + O(1) = O(n^{1 - \frac{1}{k}})\)。
证明的话,我觉得用上面的方法也是可行的。先将 \(\text{2k-side}\) 矩形化为 \(\text{k-side}\) 矩形,然后分析一下会发现对所有维度进行一轮划分后规模减半即可。
为什么 \(k \ge 3\) 不常用
分析完复杂度,我们就很好理解为什么 \(\text{3/4-D Tree}\) 甚至更高维度不常用了。
回到前面的复杂度分析,我们发现将 \(\text{2k-side}\) 矩形变成 \(\text{k-side}\) 矩形时,每次问题规模会 \(\times 2\)。
所以说 \(\text{K-D Tree}\) 暗含了一个 \(2^k\) 的常数(可能还有一个 \(k\) 的常数,存疑)。虽然 \(k = 2\) 时它基本可以忽略,但随着 \(k\) 的增大,这个常数会指数级增长。
再加上 \(\text{K-D Tree}\) 本身复杂度是 \(O(n^{1 - \frac{1}{k}})\),在 \(k\) 较大时本身与 \(O(n)\) 区别以及不大,再加上它的大常数,你就可以理解为什么有时你写了一个 \(\text{5-D Tree}\) 然后跑不过暴力了。
当然还有就是在 \(\text{OI}\) 中三维以上的题目本身就不常见,见的最多的就是数轴和平面,这也使得 \(\text{K-D Tree}\) 少了很多用武之地。
真正遇到三维问题,一般都有 \(\text{polylog}\) 做法(比如树套树,\(\text{CDQ}\) 分治),最次的也可以用一些方法(可能花费一个 \(\log\))除掉一维,再上 \(\text{2-D Tree}\),这样可以得到 \(O(\sqrt n \log n)\) 或 \(O(\sqrt n)\)(\(\text{K-D Tree}\) 的一些特点可能可以将 \(\log\) 均摊掉)的做法。
我之前还见过有人讲 \(\text{K-D Tree}\) 时直接写成 \(\text{2-D Tree}\) 的。虽然这样可能不利于理解这个数据结构,但它并不是全无道理——因为 \(k \ge 3\) 的使用场景的确太小了。
如果叫我来总结的话:
- 如果你的算法需要 \(\text{3-D Tree}\),请你务必谨慎思考是否使用,反复检查你的算法,并明确其时间复杂度为 \(O(n^{\frac{2}{3}})\),还要在计算时间复杂度时带上 \(10\) 的常数。
- 如果你的算法需要 \(\text{4D}\) 或以上的 \(\text{K-D Tree}\),请你马上放弃你现在的思路,重新思考这道题。
动态拓展
带插入
注意到建立 \(\text{k-D Tree}\) 的时间复杂度为 \(O(n \log n)\),而查询的时间复杂度为 \(O(\sqrt n)\),这是一个非常适合根号分治的结构。
设一阈值 \(B\),当插入的点 \(< B\) 个时不进行插入,而是统一存储起来,查询时算这些点对其的贡献,当插入的点达到 \(B\) 个时重构整颗 \(\text{K-D Tree}\)。
视实现情况,时间复杂度为 \(O(n \sqrt{n \log n})\) 或 \(O(n \sqrt n)\)。
好像有二进制分组的做法,复杂度差不多,但我觉得 \(\text{K-D Tree}\) 与根号分治更般配,一般二进制分组用于配合线段树之类的数据结构,可以摊掉一只 \(\log\),还能做线段树合并。所以这种方法就不展开了。
带删除
这个没什么好办法,还是只能考虑如果题目限制比较宽松的话,还是惰性删除,打个删除标记,然后定期重构吧。或者可以考虑离线。
如果题目限制严格,上面的方案无法接受,那就考虑写 \(\text{Nodey K-D Tree}\) 吧。
例题
From ix35:
给定二维平面上的 \(n\) 个点,支持两种操作 \(q\) 次:
- 将一个矩形区域内的所有点权值 \(+v\)。
- 求一个矩形区域内的点的权值的最小值。
用 \(\text{K-D Tree}\) 维护,每个矩形定位到树上的 \(O(\sqrt n)\) 点,在结点上的操作就和线段树差不多了。
时间复杂度 \(O(n \log n + q\sqrt n)\)。
功能拓展
众所周知,\(\text{K-D Tree}\) 还有一个用途是找平面最近/最远点对。
做法是枚举一个点 \(i\),在 \(\text{K-D Tree}\) 上查询最近/最远点,\(\text{K-D Tree}\) 的结构可以用来剪枝。对于 \(\text{K-D Tree}\) 上的每个结点算出一个边界矩形。则矩形内距离 \(i\) 最近/最远的点一定是矩形的四个顶点之一,如果四个顶点均不如当前 \(ans\),则无需在该子树内进行搜索。
\(k\) 近 / \(k\) 远点对的做法是类似的,用堆维护当前的前 \(k\) 优答案,还是使用类似前面的方式剪枝即可。
这样做在随机数据下表现优秀。但是它的本质还是暴力剪枝,最劣时间复杂度还是 \(O(n^2)\) 的。
二维贡献问题 / \(\text{2-D Tree}\) 分治
这个东西我初见是在 JOI Open 2018 Collapse。
考虑如下问题:
有 \(n\) 张图,每张图位于二维平面的一个位置 \((x, y)\),\(q\) 次操作,每次在一个矩形内的图中连一条边。求最终每个图的连通块数。
考虑对于一次加边操作,定位到 \(\text{K-D Tree}\) 上的 \(O(\sqrt n)\) 个结点。最后跑类似线段树分治的东西即可。
时间复杂度是 \(O(q \sqrt n \log n)\)。
与其他算法的比较
就拿 Collapse 那题来说,它其实还有另外一种做法。这里我引用一下我的题解:
首先重新描述题意:每条边 \((u, v)\) 有出现时间 \([l, r]\),每次询问在时间 \(t\),如果只保留 \([1, x]\) 和 \([x + 1, n]\) 内部的边,有多少连通块。
显然 \([1, x]\) 和 \([x + 1, n]\) 两个部分可以分别计算连通块数再相加,并且两部分是对偶的,所以我们下面只考虑计算 \([1, x]\)。
我们对所有询问按 \(t\) 排序,再对每 \(B\) 个询问分一个块,考虑对于每个块如何算答案。
考察每条边对这些询问的贡献,设这条边的出现时间为 \([l, r]\),块内询问的时间段为 \([L, R]\)。
若 \([l, r]\) 包含 \([L, R]\),则这条边对整个块都有贡献,我们将所有这样的边按 \(y\) 排序,块内的询问按 \(x\) 排序,扫描线即可。时间复杂度 \(O(\frac{qm}{B} \log n)\)。
若 \([l, r]\) 不包含但与 \([L, R]\),那么对于每条边只会落入这种情况 \(O(1)\) 次,此时我们在遇到一个询问时暴力加入这一类型的边,然后在撤销回去即可,并查集需要按秩合并。时间复杂度 \(O(mB \log n)\)。
总时间复杂度 \(O((\frac{qm}{B} + mB) \log n)\),代码中取 \(B = 333\)(随便取的,没仔细卡)。由于并查集和排序的 \(\log\) 常数很小,并且这题的加边方式很难卡满,可以通过。
考虑将这个做法套用到前面那道题目:
我们还是对所有点按 \(x\) 排序后分块,一个矩形若在 \(x\) 维度上覆盖当前块内的所有点,则对它的 \(y\) 维度扫描线,否则暴力即可。
但是此时出现了问题,Collapse 中的矩形在一个维度上是前缀,那么做扫描线的过程中只加不删。但这题是任意矩形,所以还要考虑删除的情况。显然并查集不好删除,所以还要做一遍线段树分治,那么复杂度就是 \(O(n \sqrt n \log^2 n)\) 或 \(O(n \sqrt{n \log n} \log n)\) 的,比 \(\text{K-D Tree}\) 分治多个 \(\log\)。
所以这个分块做法只适用于矩形为 \(\text{3-side}\) 时,此时时间复杂度为 \(O(n \sqrt n \log n)\)。
当然 \(\text{2-D Tree}\) 分治做法也有缺点,如果没有什么很优秀的实现的话,它的空间复杂度为 \(O(n \sqrt n)\),然后我觉得它比起分块常数略大。但它的优点是非常直观,也非常万能,可以套模板、
标签:进阶,log,text,复杂度,Tree,矩形,线段,浅谈 From: https://www.cnblogs.com/hztmax0/p/18460729