标签：le 浅谈 val DEST Segt 线段 int null ri

前言

线段树，是一种优秀的数据结构，其应用极为广泛。其中，动态开点值域线段树，配合上线段树合并，甚至能替代或超越平衡树。但是，这种线段树的树高与值域相关，很容易产生四五倍常数。无论考虑时间或空间复杂度，这样的树都不算优。那么，我们是否能想办法优化它呢？

优化思想

正如上文所述，普通线段树（本文中特指动态开点线段树，下同）的树高和值域相关。叶结点稀疏时，树上会存在若干孤链，如下图：

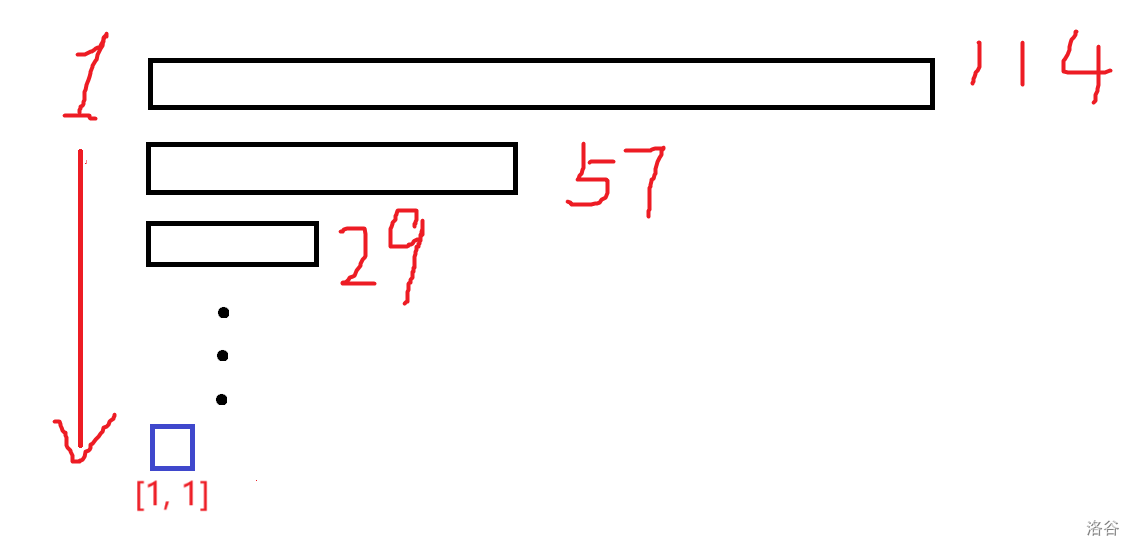
这些链唯一的作用是，连接根与叶结点。显然，这其中有巨大的优化空间。我们的思想很简单，压缩树高！准确来说，我们把任意时刻的线段树，都视为压缩后的树，并在此基础上做“扩展”。每次修改只新建少数必要的结点，从而间接起到压缩树结构的效果。

另外，为防止毒瘤数据卡结构，还需要一个“收缩”操作，动态删除无意义的叶结点，微调整棵树的结构。（虽然整棵树的结构问题不在这儿）

实现方法

首先，我们将下文中的普通线段树称为原树，将与之对应合法的、压缩后的树称为压缩树。

压缩了树高，自然丢失了区间左右端点信息。所以，我们需要在每个结点上存储，其对应的叶结点区间 $[s, t]$。为了实现方便，我们规定（很重要！）：

压缩树结点上任意的 $[s, t]$ 区间，都必须对应原树上的某一 $[l, r]$ 区间。
原树上一个点，经压缩后，只能挂在其若干级祖先的位置上。不能挂在兄弟或儿子，或其他地方。（当然，也可以直接删去）

也就是说，压缩后树上的点，必须和原树一一对应。即，压缩树结点集合到原树结点集合的映射，必须是一个单射。并且，压缩树上的任意一点，只可能是其子树内的结点。下图是一个原树与压缩树对应的例子：

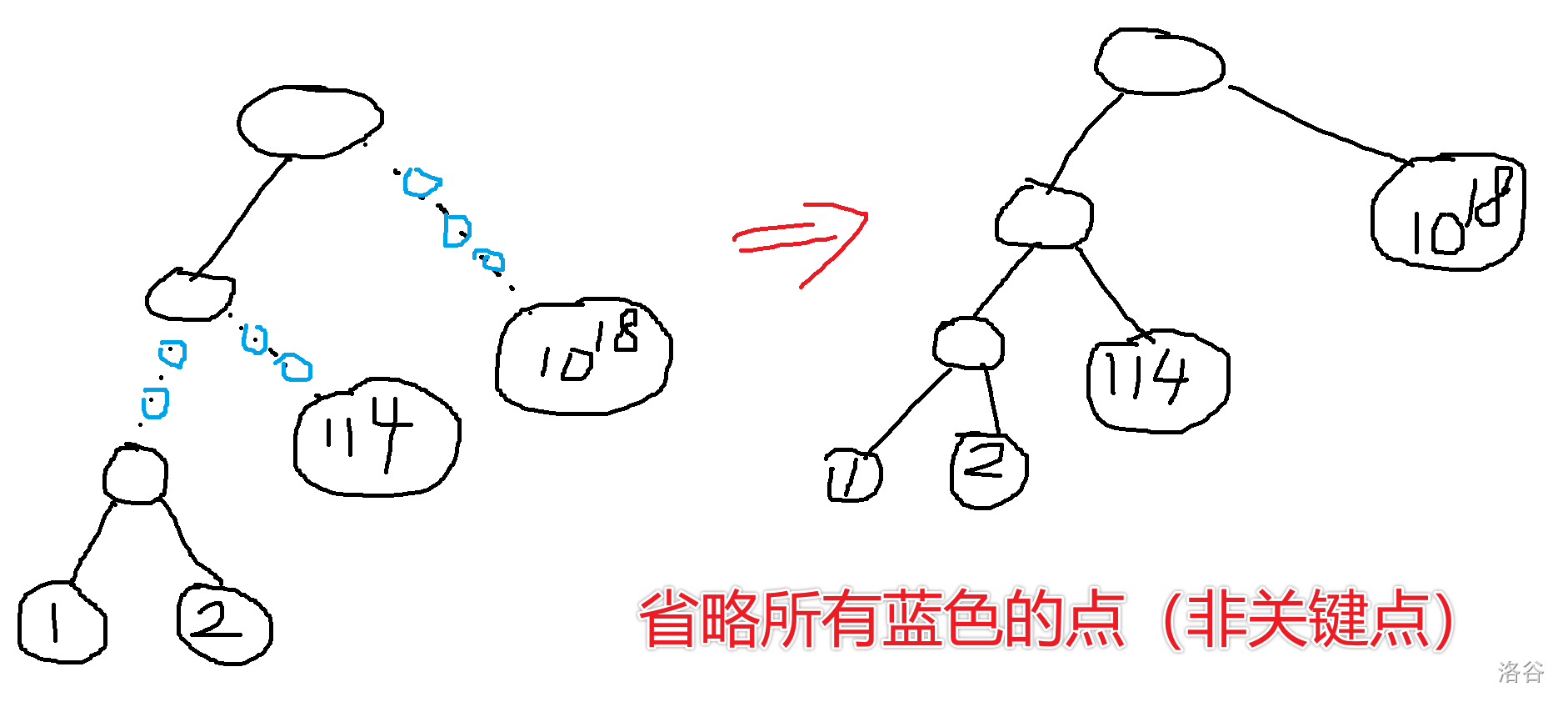
不难发现，压缩树确实比原树矮了不少。要实现这样的压缩，大力分类讨论是少不了的。在这里，我提供一种分类讨论的顺序：先空，再包含，最后相离。以这个顺序讨论，可以最大程度地简化代码。接下来我会以一棵，单点修改区间查询线段树为例，从代码层面剖析整棵树。

结点信息

如上文所述，树上结点的结构体是这样的：

struct Segt {
	int val; // 维护的区间和信息
	int s, t; // 代表 [s, t] 区间
	Segt *le, *ri; // 指向左右子结点的指针
	Segt(); Segt(int val, int s, int t, Segt* le, Segt* ri);
} null_(0, 0, 0, &null_, &null_), *null = &null_;
// 补全构造函数
Segt::Segt(): val(0), s(0), t(0), le(null), ri(null) {}
Segt::Segt(int val, int s, int t, Segt* le, Segt* ri): val(val), s(s), t(t), le(le), ri(ri) {}

需要动态开点时，本人喜欢用指针树。需要注意，最好新建一个点代表空结点，不要用 nullptr，否则很容易访问到空地址，导致 RE。

辅助函数

在介绍修改、查询、合并操作前，我们需要先实现三个辅助函数：

pushup

void pushup(Segt* u) {
	if (u->s == u->t) return; // 跳过叶子结点
	u->val = u->le->val + u->ri->val;
}

因为线段树是 Leafy Tree，所以最好别对叶子结点做 pushup。可以通过区间端点信息，辨认叶子结点。

adjust

bool adjust(int x, int y, int &l, int &r) {
	int mid = (l + r) >> 1;
	if (x <= mid && y <= mid) return r = mid, true;
	if (mid < x && mid < y) return l = mid + 1, true;
	return false;
}

在代码中使用 while(adjust(x, y, l, r));，可以快速找到一组 $[l, r]$，使得 $x \in [l, mid], y \in [mid + 1, r]$，其中 $mid = \lfloor \frac{l + r}{2} \rfloor$。也就实现了在压缩树上，遍历原树一些不必要的结点。

maintain

void maintain(Segt*& u) {
	if (u->s == u->t) {
		if (u->val == null->val) u = null;
	}
	else if (u->le == null) u = u->ri;
	else if (u->ri == null) u = u->le;
}

这个函数实现了收缩操作。但是，不收缩的压缩树，在时间上也足以应对常见的题目（可用可不用）。因此，收缩操作的优化，更多体现在空间复杂度上。

现有两种情况需要收缩：

（叶结点）点权为 0，对答案没有贡献。
（非叶结点）位于一条链上，即只有一个儿子。

另外，如果当前点非叶结点，又没有儿子，应当直接删去。不过上述代码兼容了这种情况，在实现上可以忽略。

单点修改

void update(Segt*& u, int l, int r, int pos, int val) {
	// 当前结点为空
	if (u == null) {
		u = node(pos, pos, val); // 直接新建一个叶结点，返回
		return;
	}
	// 当前结点包含待修改位置
	if (u->s <= pos && pos <= u->t) {
		// 如果是叶子
		if (u->s == u->t) {
			u->val += val;
			// maintain(u);
			return;
		}
		// 如果不是叶子，正常递归
		int mid = (u->s + u->t) >> 1;
		if (pos <= mid) update(u->le, u->s, mid, pos, val);
		else update(u->ri, mid + 1, u->t, pos, val);
	}
	// 当前结点不包含待修改位置
	else {
		while (adjust(u->s, pos, l, r)); // 在原树上找到一个合适的点 [l, r]
		Segt *v = node(pos, pos, val);
		// 此时，u v 必然在 mid = (l + r) / 2 的两边，挂上去即可
		if (v->s < u->s) swap(u, v);
		u = node(l, r, u, v);
	} 
	pushup(u);
	// maintain(u);
}

我们以 空、包含、相离 的顺序讨论，不难发现，“包含”部分的写法和普通线段树几乎一样，只是用 u->s, u->t 代替了平时的 l, r。你可以先这样理解：$[s, t]$ 才是真正的区间范围，$[l, r]$ 只是用来调整压缩树结构的。我们很贪心，只要满足条件，就新建结点并立刻返回，实在不行再递归。

区间查询

int query(Segt* u, int L, int R) {
	if (u == null) return 0;
	if (L <= u->s && u->t <= R) return u->val;
	int mid = (u->s + u->t) >> 1;
	if (R <= mid) return query(u->le, L, R);
	if (mid < L) return query(u->ri, L, R);
	return query(u->le, L, R) + query(u->ri, L, R);
}

没什么好说的，就是很普通的区间查询。特殊的是，我们已经在结点上存储了，区间左右端点的信息，因此不再需要传入 $[l, r]$ 作为函数参数。

线段树合并

Segt* merge(Segt* u, Segt* v, int l, int r) {
	if (u == null) return v;
	if (v == null) return u;
	// 保证 u 的区间长度比 v 大
	if (u->t - u->s < v->t - v->s) swap(u, v);
	// u = copy(u); 可持久化合并，在这里复制一份 u 即可
	if (u->s <= v->s && v->t <= u->t) { // 如果包含
		if (u->s == u->t) { // 叶子合并
			u->val += v->val;
			// maintain(u);
			return u;
		}
		// 非叶子合并，要判断 u 和 v 的区间关系
		int mid = (u->s + u->t) >> 1;
		// 如果 v 在 u 的半边，用 u 的一半与 v 合并，否则正常合并
		if (v->s <= mid) u->le = merge(u->le, v->t <= mid ? v : v->le, u->s, mid);
		if (mid < v->t) u->ri = merge(u->ri, mid < v->s ? v : v->ri, mid + 1, u->t);
	} else {
		// 不包含，处理方法与修改操作相同
		while (adjust(u->s, v->s, l, r));
		if (v->s < u->s) swap(u, v);
		u = node(l, r, u, v);
	}
	pushup(u);
	// maintain(u);
	return u;
}

还是 空、包含、相离 的顺序。需要注意，“包含”递归时需要特殊判断 u 和 v 的区间关系，“相离”的处理逻辑与修改操作很像，也是，先调整 $[l, r]$ 位置，再新建一个点返回。

线段树分裂

~~我不会，没写。~~ 应该可以直接分裂，回溯时用 maintain 收缩一下就好了。

完整代码

整棵树写起来并不长，分类讨论也很好记，没有很麻烦。上文中写得长，是因为有注释，稍微压行后就很短了。（合理压行）

另外，线段树如何动态开点，就不用多说了吧？看代码应该能懂。

// 结构体
struct Segt {
	int val, s, t;
	Segt *le, *ri;
	Segt(); Segt(int val, int s, int t, Segt* le, Segt* ri);
} null_(0, 0, 0, &null_, &null_), *null = &null_;
Segt::Segt(): val(0), s(0), t(0), le(null), ri(null) {}
Segt::Segt(int val, int s, int t, Segt* le, Segt* ri): val(val), s(s), t(t), le(le), ri(ri) {}

void pushup(Segt* u) {
	if (u->s == u->t) return;
	u->val = u->le->val + u->ri->val;
}

// 创建结点
Segt pool[N_ * 10]; int psz;
Segt* node() { return pool + (++psz); }
Segt* node(int val, int s, int t, Segt* le, Segt* ri) { Segt *u = node(); *u = Segt(val, s, t, le, ri); return u; }
Segt* node(int s, int t) { return node(0, s, t, null, null); }
Segt* node(int s, int t, int val) { return node(val, s, t, null, null); }
Segt* node(int s, int t, Segt* le, Segt* ri) { Segt *u = node(0, s, t, le, ri); return pushup(u), u; }

// 调整 [l, r]
bool adjust(int x, int y, int &l, int &r) {
	int mid = (l + r) >> 1;
	if (x <= mid && y <= mid) return r = mid, true;
	if (mid < x && mid < y) return l = mid + 1, true;
	return false;
}

// 收缩
void maintain(Segt*& u) {
	if (u->s == u->t) { if (u->val == null->val) u = null; }
	else if (u->le == null) u = u->ri;
	else if (u->ri == null) u = u->le;
}

// 单点修改
void update(Segt*& u, int l, int r, int pos, int val) {
	if (u == null) return u = node(pos, pos, val), void();
	if (u->s <= pos && pos <= u->t) {
		if (u->s == u->t) return u->val += val, maintain(u), void();
		int mid = (u->s + u->t) >> 1;
		if (pos <= mid) update(u->le, u->s, mid, pos, val);
		else update(u->ri, mid + 1, u->t, pos, val);
	} else {
		while (adjust(u->s, pos, l, r));
		Segt *v = node(pos, pos, val);
		if (v->s < u->s) swap(u, v);
		u = node(l, r, u, v);
	} pushup(u), maintain(u);
}

// 区间查询
int query(Segt* u, int L, int R) {
	if (u == null) return 0;
	if (L <= u->s && u->t <= R) return u->val;
	int mid = (u->s + u->t) >> 1;
	if (R <= mid) return query(u->le, L, R);
	if (mid < L) return query(u->ri, L, R);
	return query(u->le, L, R) + query(u->ri, L, R);
}

// 线段树合并
Segt* merge(Segt* u, Segt* v, int l, int r) {
	if (u == null) return v;
	if (v == null) return u;
	if (u->t - u->s < v->t - v->s) swap(u, v);
	if (u->s <= v->s && v->t <= u->t) {
		if (u->s == u->t) return u->val += v->val, maintain(u), u;
		int mid = (u->s + u->t) >> 1;
		if (v->s <= mid) u->le = merge(u->le, v->t <= mid ? v : v->le, u->s, mid);
		if (mid < v->t) u->ri = merge(u->ri, mid < v->s ? v : v->ri, mid + 1, u->t);
	} else {
		while (adjust(u->s, v->s, l, r));
		if (v->s < u->s) swap(u, v);
		u = node(l, r, u, v);
	} return pushup(u), maintain(u), u;
}

性能分析

假设存在一个问题，共有 $M$ 次操作，线段树的下标范围是 $[1, N]$。

时间复杂度

update / query

一般 $O(\log M)$；最坏 $O(\log N)$；

这里的最坏情况中，所有下标为 $2 ^ n + 1$ 的点都在线段树中，这足以将整棵树卡成一条“有用的链”。

实际的复杂度取决于树高，以及数据的分布。

merge

我不会分析。大概可以近似成两棵普通线段树合并。复杂度应该与树高相关。

空间复杂度

update / merge

严格 $O(M)$。前者每次调用最多新建两个结点，后者最多一个。

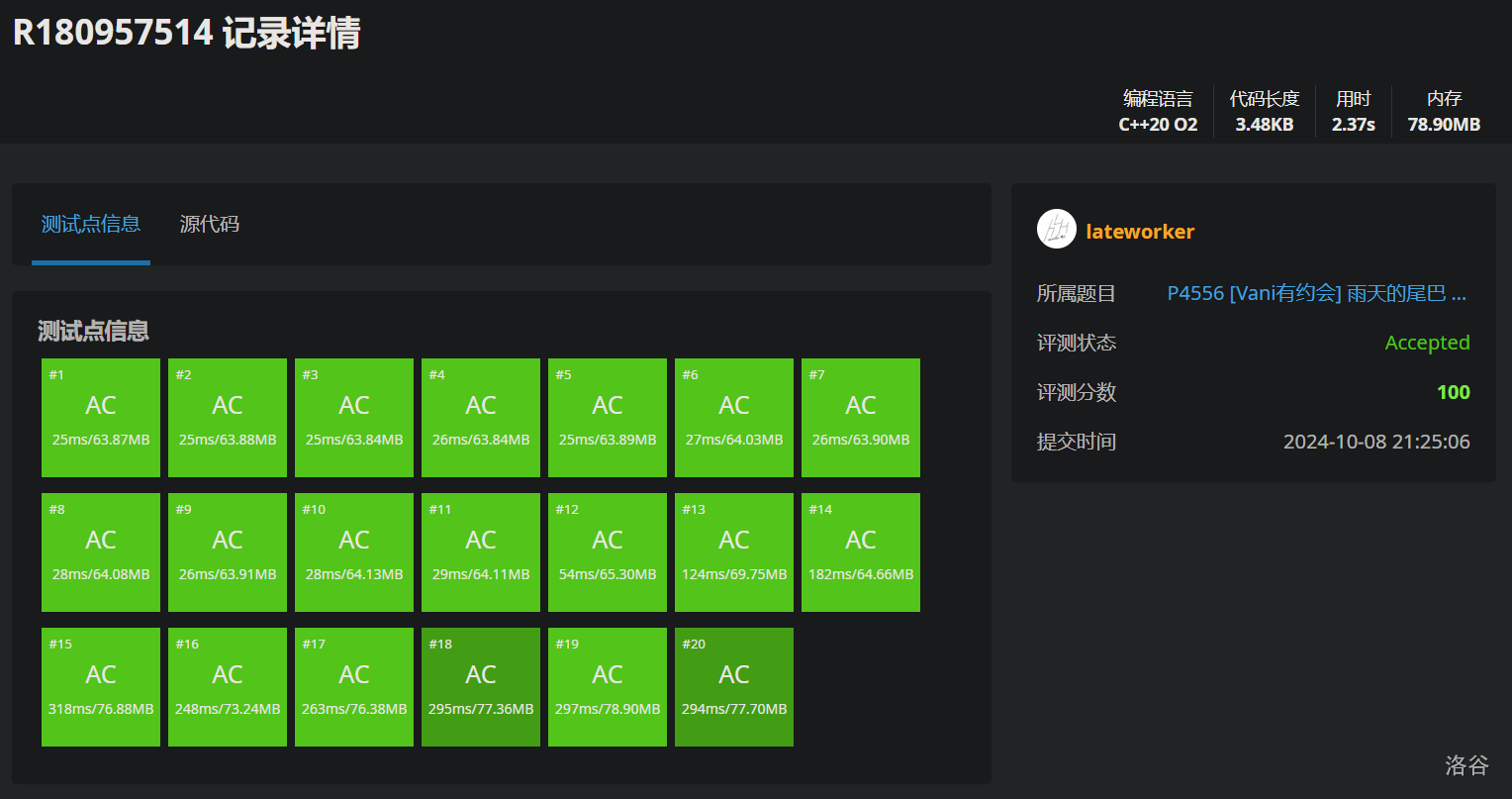
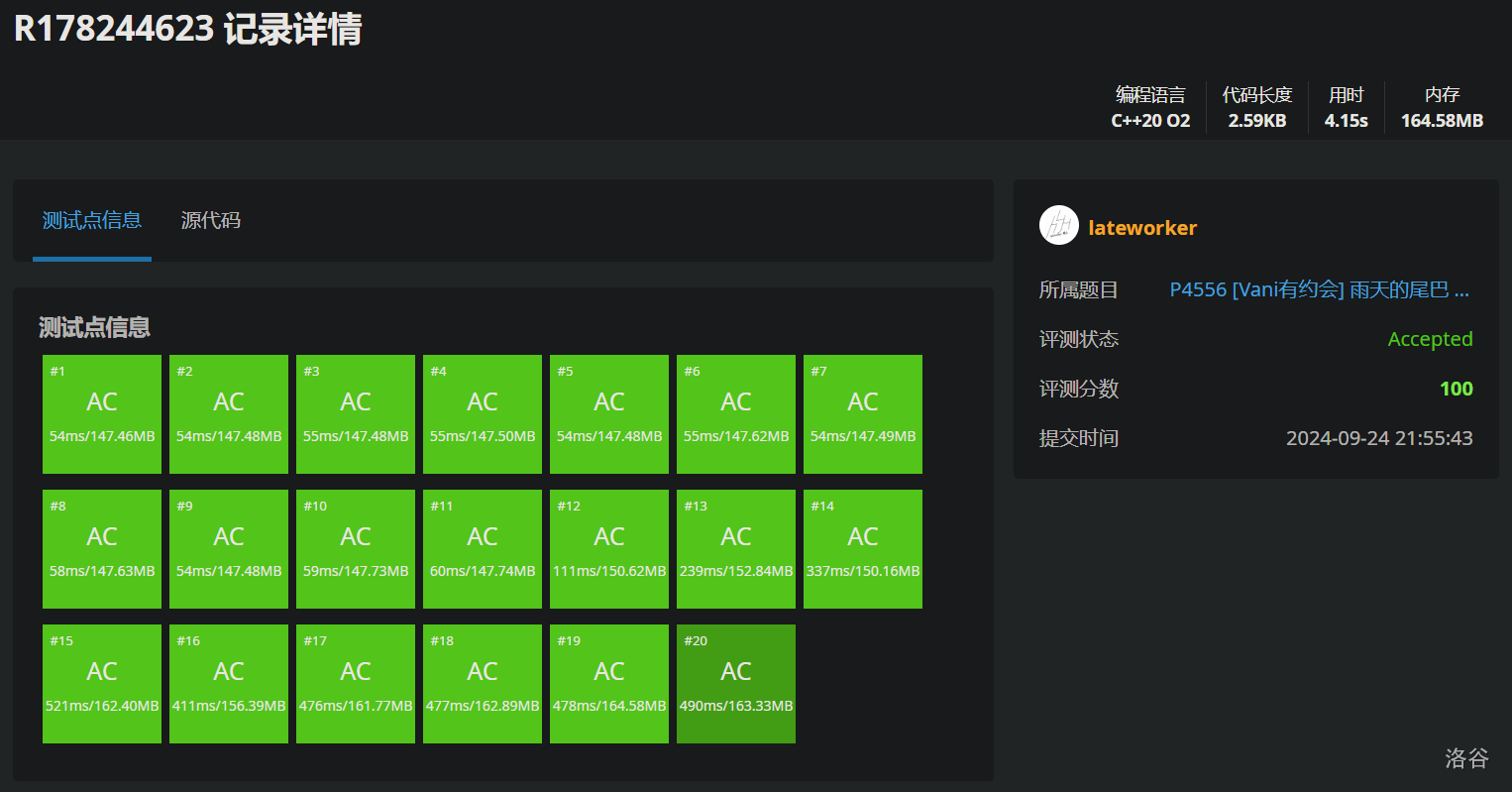
常数

显然比普通树更小。直接看对比图（线段树合并模板）：

压缩树

原树

结语

实际上，如果你的算法功底足够深厚，就会发现，压缩树其实就是原树的，一棵不严格的虚树。只不过，用虚树的方法，维护严格的虚树过于麻烦，使用扩展树高的技巧，实现起来会简单一些。如果你对严格的虚树优化感兴趣，不妨自行阅读这篇文章：浅谈维护叶子节点及其所构成的虚树的一类线段树

综上，压缩过树高的线段树，相比一般的动态开点线段树，无论在时间或空间，复杂度或常数方面，都更加优秀。并且，相比于严格的虚树实现，“扩展树”的实现显然码量更小，更容易记忆理解。我个人认为，这是一种十分普信的数据结构（优化），并且完全可以应用于实战中。

此外，本人经过几天搜索，未找到类似的文章。故单方面把这种优化后的线段树，命名为“Dest 树”（Dynamic Extension Segment Tree）。若已存在其它名字，请诸位及时告知我，以撤销本命名。

后记

分析时间复杂度时，才发现会被卡时间（空间不会）。难受了。但是，被卡总比不优化好，也算是咱研究了好几天的成果啊。最终决定，还是要写本文，将其公之于众。

标签：le,浅谈,val,DEST,Segt,线段,int,null,ri
From： https://www.cnblogs.com/lateworker/p/18459326

浅谈一类动态开点线段树优化 - DEST树

前言