A
题意:将一个圆等分为 \(K\) 分,给出其中 \(n\) 个等分点的编号,\(x_i < x_{i + 1}\)。
有向边 \(i \to j\) 存在,当且仅当 \(j\) 是距离 \(i\) 最大的点(不唯一),且与图中其他边无交点(端点不算)。
求图中最多有多少条边。\(3 \le K \le 10^9, 3 \le n \le \min(K, 10^5)\)。
引理:不存在 \(A \to B,\ C \to D\),其中 \(A, B, C, D\) 互不相同。
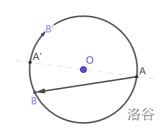
作过 \(A\) 的直径 \(AA^\prime\),作 \(B\) 关于 \(AA^\prime\) 的对称点 \(B^\prime\)
- 如果 \(C\) 或 \(D\) 在 \(\overset{\LARGE\frown}{BB^\prime}\) 上,由于大弧对大角 \(AC(D) > AB\),\(A \to B\) 的边不能存在,矛盾。
- 如果 \(\overset{\LARGE\frown}{CD}\) 包含于 \(\overset{\LARGE\frown}{AB}\),\(CB > CD\),矛盾。
- 如果 \(C\) 在 \(\overset{\LARGE\frown}{AB}\),\(D\) 在 \(\overset{\LARGE\frown}{AB^\prime}\),两边相交,不合法。
因此合法的状态只有两种:以某个点为中心的菊花状图;三条边首尾相连形成的等腰三角形。
注意两点的距离可以由对应弧长表示,也可以表示为跨过了多少整段:\(\min(\vert x_i - x_j\vert,\ K - \vert x_i - x_j\vert)\),这是个凸函数,可以二分找分界点。
求出离每个 \(i\) 距离最大的点集(最多两个),时间复杂度 \(O(n\log n)\)。(双指针能做到线性)
B
题意:给出字符串 \(s, t\),文本串 \(T\) 的权值定义为 \(s\) 作为子序列在 \(T\) 出现的次数乘上 \(t\) 作为子序列在 \(T\) 出现的此次数。
给定 \(S\),求 \(S\) 所有子串的权值和。\(\vert S\vert \le 10^5,\ \vert s\vert, \vert t\vert \le 20\)。
考虑没对子序列 \((s_1, s_2)\) 对答案的贡献(被多少区间包含),显然是第一个出现的位置乘上从最后位置开始的一个后缀长度。
设 \(f(i, j, k)\) 表示前 \(i\) 个字符,匹配到 \(s_1\) 的第 \(j\) 位,\(s_2\) 的第 \(k\) 位的开头位置和。
- \(f(i, j, k) \gets [T_i = s_{1, j} = {s_{2, k}}]\times f(i -1, j - 1, k - 1)\)。
- \(f(i, j, k) \gets [T_i = s_{1, j}]\times f(i -1, j - 1, k)\)。
- \(f(i, j, k) \gets [T_i = s_{2, k}]\times f(i -1, j, k - 1)\)。
- \(f(i, 0, 1) \gets [T_i = s_{1, 1}] \times f(i - 1, 0, 0),\ f(i, 1, 0) \gets [T_i = s_{2, 1}] \times f(i - 1, 0, 0),\ f(i, 1, 1) \gets [T_i = s_{1, 1}= s_{2, 1}] \times f(i - 1, 0, 0)\)。
- \(f(i, j, k) \gets f(i -1, j, k)\)。
考虑以 \(i\) 结尾的贡献,不能由第四种转移过来(因为对应方案 \(i\) 不是结尾),前四种转移过后的 \(f(i, \vert s_1\vert, \vert s_2\vert)\) 乘上 \(\vert T\vert - i + 1\)。
C
定义函数:
\[f(u, x, y) = \begin{cases} u - y & x = 1\\ u& 1 < x \le y,\ x \perp y\\ -x \times y& x \ne 1,\ x \mid y\\ 0 & \text{otherwise} \end{cases} \]给定长度为 \(n\) 的数组 \(a\),定义一段区间 \([l, r]\) 的优美度等于:
\[\sum_{i = 1}^{10^6}\sum_{j = l}^{r} f(u, i, a_j) \]\(q\) 次询问,每次给出 \(l\) 和参数 \(u\),求 \(r \ge l\) 的最大优美度,以及对应最小的 \(r\)。
数据范围:\(n, q \le 5 \times 10^5,\ 1 \le a_i \le 10^6,\ 1 \le u_i \le 1.8 \times 10^7\)。
交换一下求和号:
\[\sum_{j = l}^{r}\sum_{i = 1}^{10^6} f(u, i, a_j) \] 标签:prime,10,le,vert,30,CSP2024,times,gets From: https://www.cnblogs.com/Luxinze/p/18442974