「Wdoi-(-1)」恋弹者们的黑集市
魔理沙有两种方法移动这个骰子:将骰子向下一列翻转,或者向下一行翻转。值得注意的是,翻转骰子后,骰子每面上的数字就会随着翻滚而改变。现在魔理沙需要将骰子滚动至第 \(n\) 行第 \(m\) 列。
魔理沙的分数被定义为,所有时刻,骰子与棋盘上的数字接触的那一面的数字,乘上棋盘上该数字,再累加起来的和。只有魔理沙最大化这个和,她才能获取她所需要的卡片。
你能帮帮魔理沙吗?
简要题意
有一个 \(n\times m\) 大小的棋盘,第 \(i\) 行第 \(j\) 列写有数字 \(a_{i-1,j-1}\)。
现在有一个骰子,六个面按照前、后、左、右、上、下的顺序,依次写有数字 \(w_0,w_1,w_2,w_3,w_4,w_5\)。现在骰子摆放在 \((0,0)\) 位置,需要将它滚动至 \((n-1,m-1)\)。

骰子只有两种方式滚动:向下一行翻滚、向下一列翻滚。我们记一种方案的权值为,整个过程中(包括骰子在起点和终点时),骰子最底面上写着的数字,与此时骰子所在格子上写着的数字的乘积之和。
思路
\(dp\),我们很自然的会想到使用 \(dp_{i,j}\) 来表示骰子到达 \((i,j)\) 点的可以获得的最大权值,但是我们无法确定到达这一点时魔方的“方向”,这也就提示我们要把“魔方的状态”这个东西设计进转移方程式里面。
我们发现,我们只需要两个从正方体中心出发的两条垂直的有向射线就可以确定这个骰子的六个面了。
于是我们更改一下状态的设计,用 \(dp_{i,j,k,h}\) 表示骰子到了 \((i,j)\) 点,编号为 \(k\) 的面朝下,编号 \(h\) 的面朝前所能得到的最大权值。
我们知道 \(dp_{i,j}\) 会从 \(dp_{i - 1,j}\) 和 \(dp_{i,j - 1}\) 转移过来,也就是说骰子会从右边翻过来或者从上面翻下来。
图示:
点 \((i,j)\):
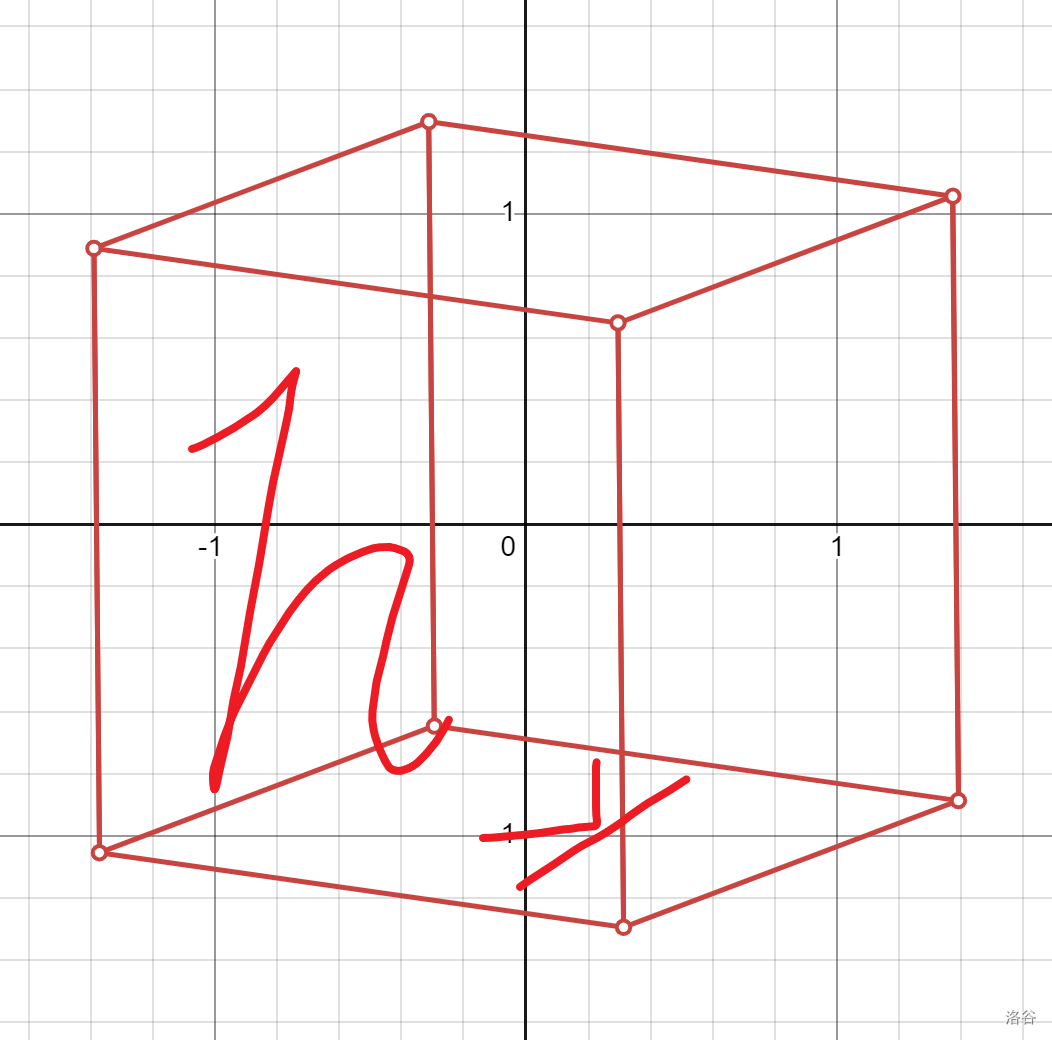
从 \((i - 1,j)\) 翻下来:
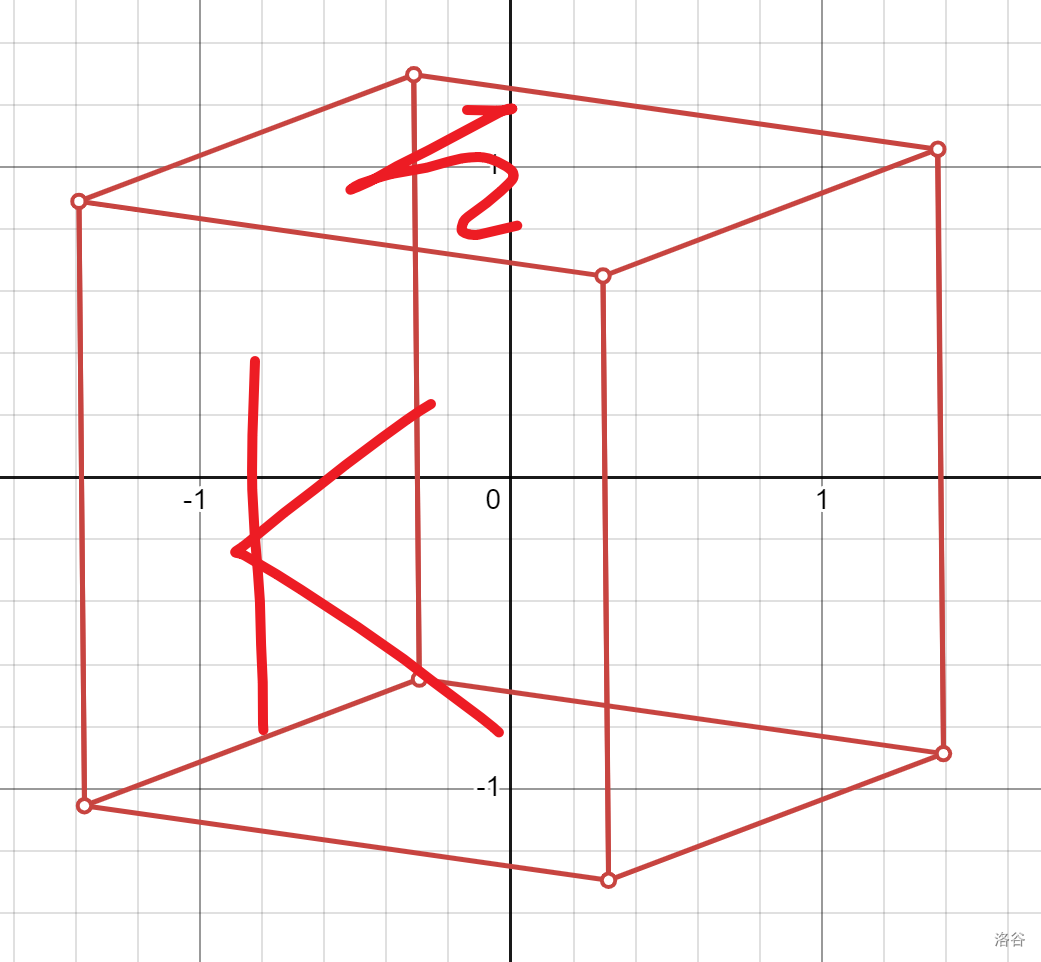
从 \((i,j - 1)\) 翻到右边:
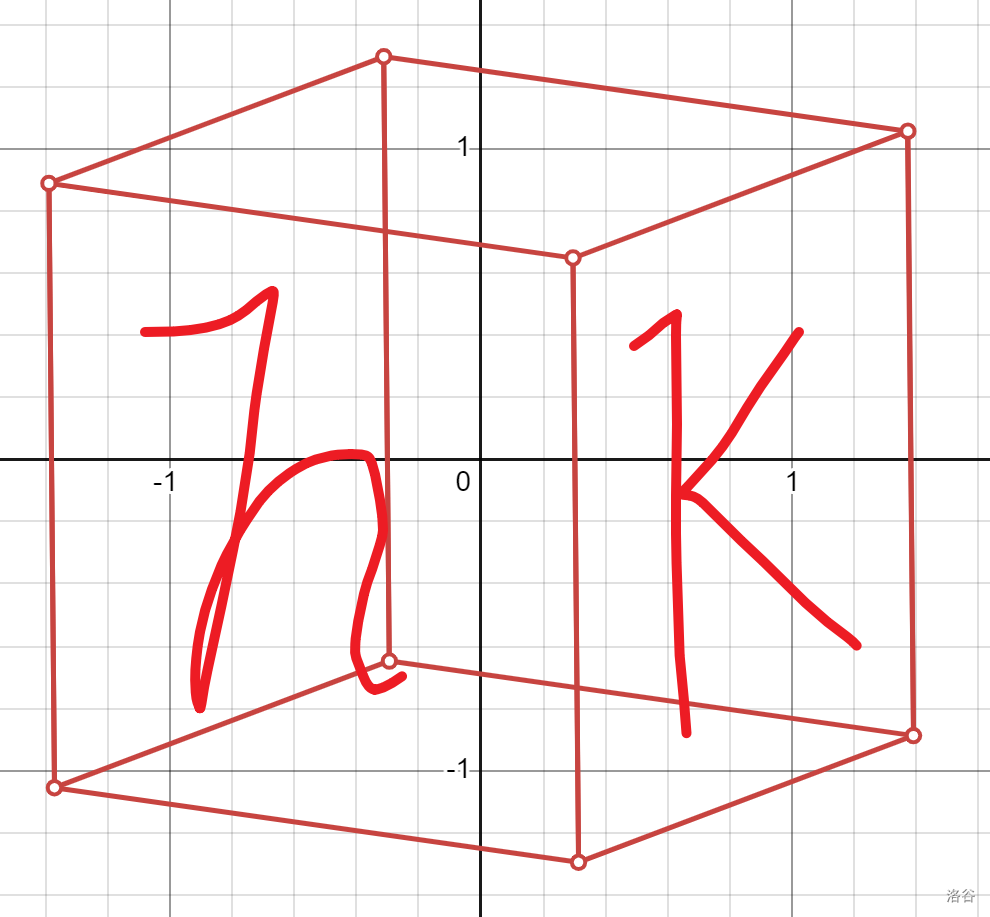
其中图 \(2\) 的状态是 \(dp_{i - 1,j,f(h),k}\),而图三的状态可以表示为 \(dp_{i.j - 1,g(h,k),h}\) 。
其中 \(f(h)\) 表示 \(h\) 面的对面,而 \(g(h,k)\) 表示以 \(h\) 面作为前面,\(k\) 面作为右边,这个状态立方体的下面。
而 \(f(h)\),\(g(h,k)\) 都可以提前预处理出来。
所以可以得到状态转移式:
\[dp_{i,j,k,h} = \max(dp_{i,j,k,h} , \max(dp_{i - 1,j,f(h),k},dp_{i,j - 1,g(h,k),h}) + w_k \times val_{i,j}) \]此题完结,注意初始状态是第一张图的状态。
\(code\)
#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN = 1e3 + 7;
const long long INF = -2e9;
const int rd[6] = {1,0,3,2,5,4};
const int cd[6][6] = {
{-1 ,-1 ,4 ,5 ,3 ,2},
{-1 ,-1 ,5 ,4 ,2 ,3},
{5 ,4 ,-1 ,-1 ,0 ,1},
{4 ,5 ,-1 ,-1 ,1 ,0},
{2 ,3 ,1 ,0 ,-1 ,-1},
{3 ,2 ,0 ,1 ,-1 ,-1},
};
int n,m;
int val[MAXN][MAXN];
int dp[MAXN][MAXN][6][6];
int w[MAXN];
int f(int x){ return rd[x]; }
int g(int h,int k){ return cd[h][k]; }
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>m;
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
cin>>val[i][j];
}
}
for(int i = 0;i <= 5;i++){
cin>>w[i];
}
for(int i = 0;i <= n;i++){
for(int j = 0;j <= m;j++){
for(int k = 0;k <= 5;k++){
for(int h = 0;h <= 5;h++){
dp[i][j][k][h] = INF;
}
}
}
}
dp[1][1][5][0] = w[5] * val[1][1];
for(int i = 1;i <= n;i++){
for(int j = 1;j <= m;j++){
if(i == j && i == 1) continue;
for(int k = 0;k <= 5;k++){
for(int h = 0;h <= 5;h++){
if(g(h,k) == -1) continue;
dp[i][j][k][h] = max(dp[i][j][k][h] , max(dp[i - 1][j][f(h)][k],dp[i][j - 1][g(h,k)][h]) + w[k] * val[i][j]);
}
}
}
}
int ans = INF;
for(int i = 0;i <= 5;i++){
for(int j = 0;j <= 5;j++){
ans = max(ans,dp[n][m][i][j]);
}
}
cout<<ans;
return 0;
}