2A
题意:给定长度为 \(n\) 的非负整数数组 \(a\),求最小的 \(r−l+1\) 满足 \(l≤r,\sum_{i = l}^ra_i\) 是合数。
考虑全是正数的情况,答案一定 \(\le 4\),考虑一下每个数的奇偶性即可。
那么就把所有正数及其位置存下来,使得 \(b_i = a_{p_i}\),暴力检查 \(b\) 中长度为 2/3 的段,和 \(p_{i + 3} - p_i + 1\) 取 min。submission
A
题意:给定数组 \(a, b\),设 \(f_i(x)= \max(x + a_i, b_ix)\)。每次给出 \(l, r, x\),求 \(f_r(f_{r - 1}(\cdots f_l(x)\cdots)) \bmod p\)。
如果 \(b_i = 1\),肯定选 \(x + a_i\);否则需要决策哪个更大,注意到当 \(x > p\) 时一定是 \(b_ix\) 更大。
因此暴力跳 \(\log p\) 次 \(b_i > 1\) 的位置, 然后线段树维护一次函数复合得到剩余部分。submission
B
题意:给出 \(n\),\(q\) 次询问。求边长为有理数且四个顶点均为两个坐标均在 \([1,n]\) 内的整点且其中一个坐标为 \((x,y)\) 的正方形个数。
边长不是整数就是无理数。考虑边与坐标轴不平行的情况。
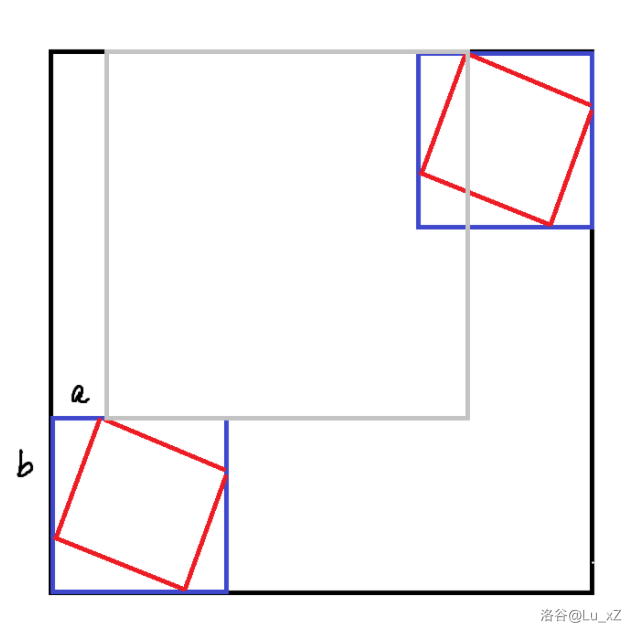
补全下图红色正方形,四角是全等的勾股三角形。当 \((x, y)\) 作为该正方形最上面的角时,\((a, b)\) 回到一个矩形区域有 \(1\) 的贡献(灰色)。
其他三个角同理。如果 \(a + b < n\) 的勾股数对数足够小,那么直接枚举,做若干矩形覆盖,这是经典的二维数点问题。
考虑勾股数 \(a^2 + b^2 = c^2\),设 \(x = c + b,\ y = c - b\)。
\[a = \sqrt{xy},\ b = \dfrac{x - y}{2},\ c = \dfrac{x + y}{2} \]枚举所有正整数 \(x, y\) 可以生成所有勾股数。
设 \(n = \sqrt{\dfrac{x}{2}},\ m = \sqrt{\dfrac{y}{2}}\):
\[a = 2nm,\ b = n^2 - m^2,\ c = n^2 + m^2 \]枚举所有正实数 \(n, m\) 可以生成所有勾股数。
考虑本源勾股数 \((a, b, c)\),满足 \(a, b, c\) 两两互质,其他勾股数都能用 \((ka, kb, kc)\) 表示。
其中,一定有 \(a, b\) 一奇一偶:都是偶数,有公因子;两奇,则 \(c\) 是偶数,\(a^2 + b^2 \not\equiv c^2\pmod 4\),矛盾。
如果 \(a\) 偶 \(b\) 奇,则 \(x, y\) 都是偶数,又因为 \(b, c\) 互质,所以 \(\dfrac{x}{2}, \dfrac{y}{2}\) 互质。又由于 \(nm\) 是整数,\(n, m\) 只能都是整数。
如果 \(a\) 奇 \(b\) 偶,\(x, y\) 都是奇数,\(n, m\) 不可能是整数。
枚举正整数 \(n, m\),可以生成所有本源勾股数 \((a, b, c)\) 恰好一次。
\(c = \sqrt{a^2 + b^2} < a + b < N\)。\(n^2 + m^2 = c \le \sqrt N \implies n, m \le \sqrt N\),只有 \(O(N)\) 对。
对于 \((ka, kb, kc)\) 必须满足 \(k \le \frac{N}{a + b}\),\(a + b\) 相同的本源勾股数应该只有 \(O(1)\) 对,最后会生成 \(O(N\log N)\) 对勾股数。
C
题意: