P11037 【MX-X3-T4】「RiOI-4」上课
本文主要解释不断 \(+1\) 的过程如何快速实现的具体流程。
题意
给定正整数 \(n,q\) 和 \(n\) 个区间 \([l_i,r_i]\)。
有 \(q\) 组询问,每次询问给定一个整数 \(x\)。在每个区间内选择一个整数 \(a_i\)(\(l_i\leq a_i\leq r_i\)),使得所选整数的总和等于 \(x\),并使得选出的 \(a\) 序列的方差最小。输出方差最小值,对 \(998\,244\,353\) 取模。保证存在至少一种合法的选取方案。
输入格式
第一行两个正整数 \(n,q\)。
接下来的 \(n\) 行,每行两个自然数 \(l_i,r_i\)。
最后 \(q\) 行,每行一个整数 \(x\),表示一次询问。保证存在至少一种合法的选取方案。
输出格式
\(q\) 行,每行一个整数,表示最小方差对 \(998\,244\,353\) 取模的值。
样例 #1
样例输入 #1
3 3
1 3
2 3
3 5
6
9
11
样例输出 #1
665496236
0
554580197
样例 #2
样例输入 #2
4 3
1 4
11 12
3 9
6 10
21
29
26
样例输出 #2
811073551
811073543
748683272
提示
【样例解释 #1】
询问一方差最小的选择方案为 \({1,2,3}\),最小方差为 \(\frac{2}{3}\),有 \(665\,496\,236\times3\equiv 2\pmod{998\,244\,353}\),故输出 \(665\,496\,236\)。
询问二方差最小的选择方案为 \({3,3,3}\),最小方差为 \(0\),有 \(0\times1\equiv 0\pmod {998\,244\,353}\),故输出 \(0\)。
询问三方差最小的选择方案为 \({3,3,5}\),最小方差为 \(\frac{8}{9}\),有 \(554\,580\,197\times9\equiv 8\pmod{998\,244\,353}\),故输出 \(554\,580\,197\)。
【数据范围】
本题开启捆绑测试。
| 子任务 | 分数 | \(n\) | \(q\) | 特殊性质 |
|---|---|---|---|---|
| \(1\) | \(9\) | \(\le5\) | \(\le5\) | \(r_i\le5\) |
| \(2\) | \(13\) | \(\le2\times10^3\) | \(\le2\times10^3\) | \(r_i\le2\times10^3\) |
| \(3\) | \(16\) | \(\le10^6\) | \(=1\) | |
| \(4\) | \(25\) | \(\le10^5\) | \(\le10^5\) | \(r_i\le10^5\) |
| \(5\) | \(37\) | \(\le10^6\) | \(\le10^6\) |
对于所有数据,满足 \(1\leq n,q\leq 10^6\),\(0\leq l_i\leq r_i\leq 10^{6}\),对于每个 \(x\) 保证存在一种合法的方案。
核心
最重要的一个式子,有点类似于高中时学回归方程的时候学过的 \(\frac{\Sigma(x_i-\overline{x_i})^2}{\Sigma(y^2_i-\overline{y_i})^2}\),其中 \({\Sigma(x_i-\overline{x})^2}=\Sigma{x_i^2}-2\Sigma x_i\cdot{\overline x}+n\cdot \overline{x}^2=\Sigma{x_i^2}-2n\cdot \overline{x}^2+n\cdot \overline{x}^2\),也就是 \(\Sigma{x_i^2}-n\cdot \overline{x}^2\) 。
所以本题中的方差可以变成 \(\frac{\Sigma x_i^2}{n}-\overline x^2\) ,对于每一个询问的 \(\overline x^2\) 是固定的,所以要最小化的就是平方和 \(\Sigma x_i^2\) ,为了达到这个目的很显然的一个贪心就是让所有 \(a_i\) 取最小值 \(l_i\) ,设此时他们的和为 \(S_0\) ,那么我们还剩下 \(x-S_0\) 的数值要分配给这些 \(a_i\) ,那么只用把 \(x-S_0\) 依次分配给最小的 \(a_i\) 即可。
注意这里可能有理解上的偏差,并不能在排序过后按照 \(l_1,l_2...l_n\) 的顺序依次将他们变成 \(r_1,r_2...r_n\) ,直到不能操作为止,因为每次 \(+1\) 之后最小值都有可能变化;而是取出每次给最小值 \(a_{min}\) 加上 \(1\) 之后的序列中的最小值 \(a'_{min}\) 循环地动态进行该操作,否则你就只能在 \(subtask1\) 上 AC 两个点。
按照该过程手玩一下样例就会发现这实际上类似于一个倒水的过程,拿样例一举个例子的话(红线为初始值),可以具象为如下模型:
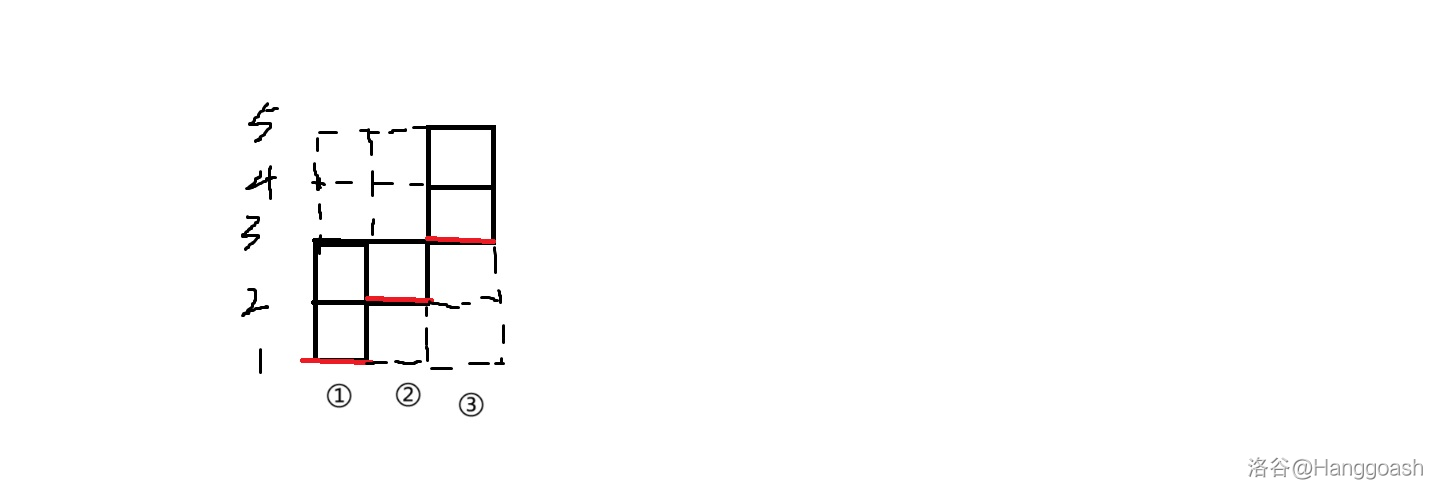
现在如果倒水进去,把最高液面的高度变为 \(4\) ,也就相当于对 \(a_i\) 们进行若干次操作后使得 \(\max a_i=4\),就会变成这样 :
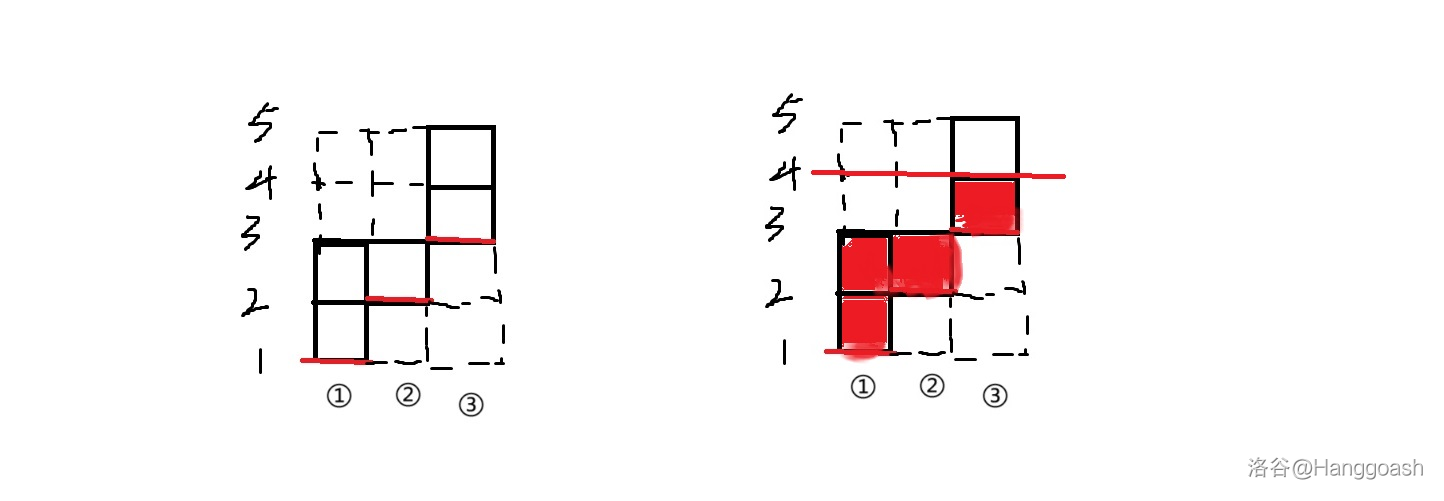
其中我们花费的代价为 \(4\) ,也就是 \(4\) 个红格子。
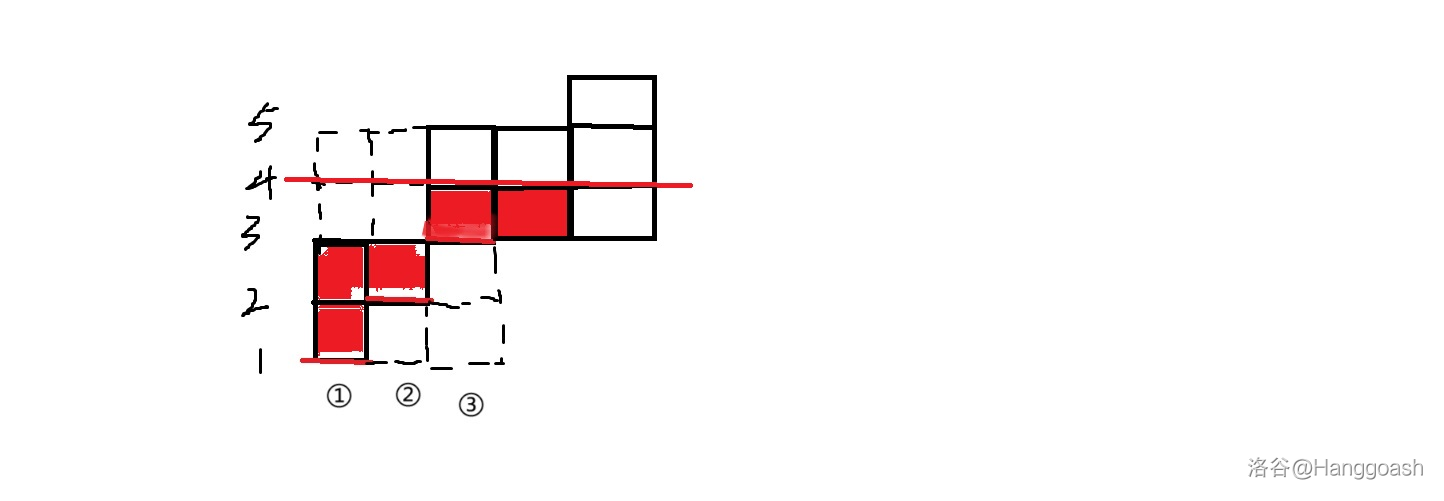
那在这个问题中,我们一共需要花费的代价是 \(x-S_0\) ,很显然的是这个最后的最高高度是具有单调性的,也就是说总是存在一个 \(h\) ,使得在花费完 \(x-S_0\) 的代价后,最高液面 (最大的 \(a_i\) )能够达到 \(h\) ,但无法达到 \(h+1\) 。(注意最高一层的液面不一定都能恰好取到最大值,因为“液面”高度是用整数而不是小数来衡量的,比如下图这种 \(x-S_0=5\) 的情况) ,所以可以采取二分。
至于在二分内部的判断方式,我们可以定义一个 \(sum[h]\) 数组,表示将所有 \(l_i\) 提高到 \(\min{(h,r_i)}\) 的代价,可以想到维护 \(sum[h]\) 数组的方式就是根据 \([l_i,r_i]\) 依次在 \(sum[h]\) 内进行区间内每个数 \(+1\) 的操作 ,最后算出每个位置对应的值,再前缀和即可,可以在读入的时候就维护差分数组,再做两次前缀和的方式实现,不会的话请移步 P2367 。
统计答案
显然是不能够暴力枚举的,思考一下发现,如果我们现在算出了最大高度为 \(h\) :
对于 \(r_i<h\) 的所有(显而易见,不可取等)区间 :其对应的 \(a_i\) 必取 \(r_i\) ,对答案的贡献为 \(r_i^2\) 。
对于 \(h\le l_i\) 的所有(显而易见,可以取等)区间:其对应的 \(a_i\) 必取 \(l_i\) ,贡献为 \(l_i^2\) 。
对于其他的所有区间:
其 \(a_i\) 的可能取值为 \(h\) 或 \(h-1\) ,有 \(sum[h]-(x-S_0)\) 个 \(h-1\) , \((x-S_0)-sum[h-1]\) 个 \(h\),可以 \(O(1)\) 地统计。
前两种情况可以定义 \(Rans[h]\) 为高度为 \(h\) 时,\(\Sigma_i^{r_i<h} r_i^2\) ; \(Lans[h]\) 亦是如此。
由于一个 \(r_i\) 可以对所有比它大的高度产生贡献,符合区间加的特性,所以同样可以用差分的方式预处理求出。
小细节
涉及到逆元的最好开个 \(longlong\) ,尤其是在模数比较大的情况下,任何可能会爆的地方最好都取个模。
然后由于 \(sum,Lans,Rans\) 的下标都对应的是高度而不是编号 ,所以枚举的时候应该是从 \(L_{min}\) 到 \(R_{max}\)
Code
代码仅供参考,有些小地方的实现可能不同,不过不影响。
#include<bits/stdc++.h>
#define int long long
#define rr register
using namespace std;
const int MOD=998244353;
template<typename T>inline void re(T &x)
{
x=0;
int f=1;char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
x*=f;
}
template<typename T>inline void wr(T x)
{
if(x>9)wr(x/10);
putchar(x%10^48);
}
inline int power(int a,int b)
{
int ans=1;
while(b)
{
if(b&1)ans=ans*a%MOD;
a=a*a%MOD;
b/=2;
}
return ans%MOD;
}
const int N=1e6+10;
pair<int,int> q[N];
int sum[N],lsum[N],rsum[N],lcnt[N],rcnt[N];
int L=1e6+10,R=-1;
int n,tn,Q,S;
inline void add(int l,int r)
{
sum[l]++,sum[r]--;
}
inline void pre()
{
re(n),re(Q);
//sum
for(rr int i=1;i<=n;++i)
re(q[i].first),re(q[i].second),add(q[i].first,q[i].second),L=min(L,q[i].first),R=max(R,q[i].second),S+=q[i].first;
for(rr int i=L;i<=R;++i)sum[i]=sum[i-1]+sum[i];
for(rr int i=L;i<=R;++i)sum[i]=sum[i-1]+sum[i];
//cnt&sum_ans
int l,r,tmp;
for(rr int i=1;i<=n;++i)
{
l=q[i].first,r=q[i].second;
rcnt[r+1]++,rcnt[R+1]--;
lcnt[L]++,lcnt[l+1]--;
tmp=l*l%MOD,lsum[L]=(lsum[L]+tmp)%MOD,lsum[l+1]=(lsum[l+1]-tmp+MOD)%MOD;
tmp=r*r%MOD,rsum[r+1]=(rsum[r+1]+tmp)%MOD,rsum[R+1]=(rsum[R+1]-tmp+MOD)%MOD;
}
for(rr int i=L;i<=R;++i)
{
lcnt[i]+=lcnt[i-1],rcnt[i]+=rcnt[i-1];
lsum[i]+=lsum[i-1],lsum[i]%=MOD;
rsum[i]+=rsum[i-1],rsum[i]%=MOD;
}
//n^(-1)
tn=power(n,MOD-2);
}
//第一个大于等于
inline int find(int x,int l,int r)
{
if(l>=r)return l;
int mid=(l+r)/2;
if(sum[mid-1]>=x)return find(x,l,mid);
else return find(x,mid+1,r);
}
inline int solve(int x)
{
int ans1,ans2;
int h=find(x-S,L,R);
int res=n-rcnt[h]-lcnt[h],cnt=sum[h-1]-x+S;
ans1=(rsum[h]+lsum[h])%MOD,ans1+=(h-1)*(h-1)%MOD*cnt%MOD+h*h%MOD*(res-cnt)%MOD,ans1=ans1%MOD*tn%MOD;
ans2=(MOD-power(x%MOD,2)*power(tn,2)%MOD)%MOD;
return (ans1+ans2)%MOD;
}
signed main()
{
pre();
int x;
while(Q--)
{
re(x);
wr(solve(x)),putchar('\n');
}
return 0;
}