See through Gradients. Image Batch Recovery via GradInversion
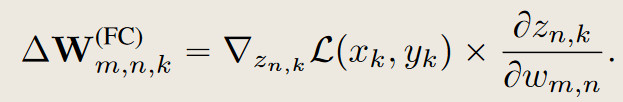
\(W^{FC} \in \mathbb{R}^{M \times N}\),其输入为一个M维向量\(v \in \mathbb{R} ^M\),\(\Delta W^{FC}_{m,n,k}\)是损失函数对全连接层\(W\)的导数。
对于一个特定的类别\(n\),(\(z\)为全连接层输出的logits),其输出\(z_n=v \cdot W[:,n]=\sum_{i=1}^M v_iw_{i,n}\),那么有\(\frac{\partial{z_{n,k}}}{\partial{w_{m,n}}}=\frac{\partial{\sum_{i=1}^M v_iw_{i,n}}}{\partial{w_{m,n}}}=v_m\),
\(v_m\)也就是\(o_m,k\),即全连接层的第\(m\)个输入。这里的m和n其实是W参数的索引。
设全连接层输入是\([v1,v2,v3]\),参数为\(\begin{bmatrix}
w_{11} \cdots w_{1N} \\
w_{21} \cdots w_{2N} \\
\cdots \\
w_{M_1} \cdots w_{MN}
\end{bmatrix}\),设样本的类别是\(n\),则与\(n\)对应的等式为\(\partial\{v_1w_{1n}+v_2w_{2n}+v3w_{3n}\}/\partial\{w_{m,n}\}=v_m\),其中n是固定的。
其实这就是idlg的另一种写法,只不过更细了。
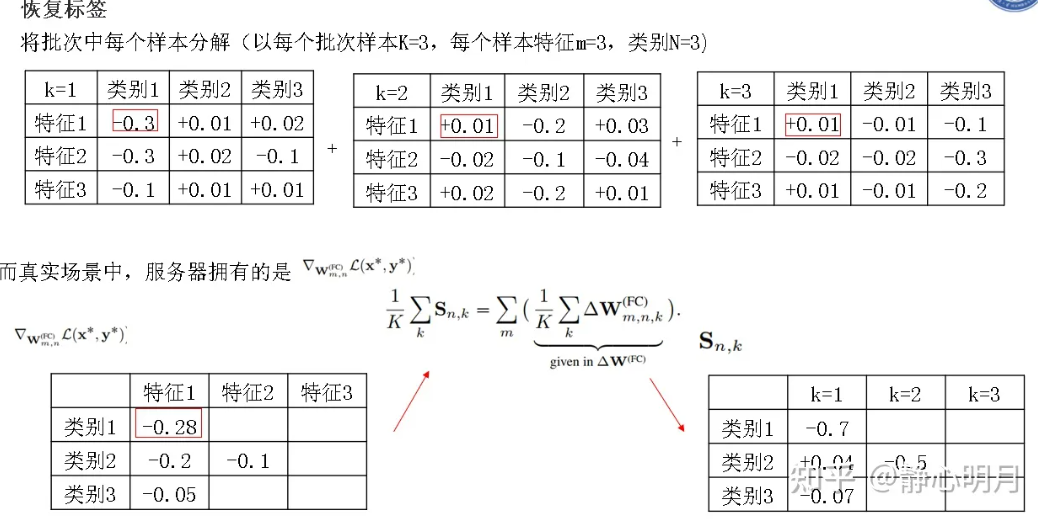

我的理解:\(S_{n,k}\)是一个数,是由\(x_k\)这个数据的损失在logits \(n\)上的梯度导数相加而来(按照特征维度\(m\)),当\(n=n_k^*(groud-truth)\)时,加数都是负数,那么\(S_{n,k}<0\),对应着真实标签;
非\(n_k^*\)标签时对应的\(S_{n,k}>0\),\(S=\{S_{n,k}\}\)就是一个\(N \times K\)矩阵,每一列对应一个数据\(x_k\)对不同logits的梯度,每一列中只有一个负数对应着\(x_k\)的真实类别。
关键:从上面图片中看到,\(\triangle \mathbf{W}^{FC}\)是\(K\)个样本的平均梯度,单个样本的梯度中有一列都是负数,根据观察\(|S_{n_k^*,k}|>>|S_{n\neq n_k^*,k}|\),根据原文"This leaves a negative sign mostly intact when the summation brings in positive values from other images.",当求和从其他图像中引入正值时,会留下大部分完整的负号,也就是说在真实的梯度\(\triangle \mathbf{W}^{FC} \in \mathbb{R}^{M \times N}\)中,真实标签对应的列会保留大量的负号,也就是说,多个样本的梯度聚合之后,负的部分仍然是负的,可显示出原始标签的信息。
为了使得这种负号的标志更鲁棒,文章使用了逐列的最小值,而不是按照特征维度进行求和
取每一列中最小值后的向量具有\(N\)维,从小到大排序,\(argsort\)记录对应的列号,直接返回前\(K\)个值,也就对应着\(K\)个样本的类别
注意返回的是batch中\(K\)个样本的类别,并不能一一对应,因为只给定了平均梯度。而且有个假设就是一个批次中不能有重复的标签数据。
真实性正则化
文中加入了一个正则化项(R_{fidelity}(\cdot)),来驱使生成的(\hat{x})尽可能保持真实,具体形式为:
[ R_{fidelity}(\hat{x}) = \alpha_{tv}R_{TV}(\hat{x}) + \alpha_{l_2}R_{l_2}(\hat{x}) + \alpha_{BN}R_{BN}(\hat{x})]
其中(R_{TV})和(R_{l_2})分别惩罚图像的方差和(L2)范数,属于标准的图像先验。
DeepInversion中关键的部分就是使用了BN的先验来进行约束
[ R_{BN}(\hat{x}) = \sum_l||\mu_l(\hat{x}) - BN(mean)||_2 + \sum_l||\sigma^2_l(\hat{x}) - BN(variance)||_2]
其中(\mu_l(x))和(\sigma^2_l(x))是第(l)层卷积的,对于一个批数据的均值和方差的估计,这种真实性的正则化能够使图片变得更加真实。
组一致性正则化
在训练数据恢复的时候,有一个挑战就是物体实际位置的确定,如

在实验中,作者使用了不同的随机种子进行图像的还原,结果产生不同程度上的偏移,但这些样本其实语义上都是一致的。
基于这个观察,作者提出了一种组一致性的正则化方法,也就是用不同的随机种子生成,然后对这些结果进行融合。
其正则化形式为:
\[\mathcal{R}_{group}(\hat{x},\hat{x}_{g\in G})=\alpha_{group}\|\hat{x}-\mathbb{E}(\hat{x}_{g\in G})\|_2 \]其中,需要计算这个期望\(\mathbb{E}(\hat{x}_{g\in G})\),其实就是平均期望。
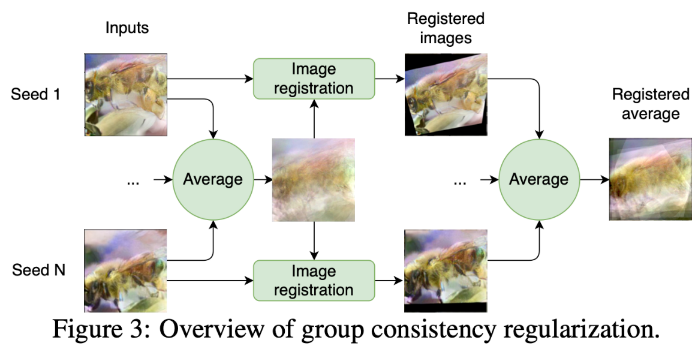
如上图所示,首先按像素进行平均,得到一张平均图像,然后所有图像根据这个平均图像进行对齐,之后再取一次平均,得到最后的对齐后的平均图像。
\[\mathbb{E}(\hat{x}_{g\in G})=\frac{1}{|G|}\sum_{g}F_{\hat{x}_g\rightarrow\frac{1}{|G|}\sum_g\hat{x}_g}(\hat{x}_g). \]Final Update
文中使用的是一种基于能量的模型,受 Langevin 的启发,具体形式为
\(\begin{aligned}
&\Delta_{\hat{x}^{(t)}} \gets -\nabla_{\hat{x}}(\mathcal{L}_{grad}(\hat{x}^{(t-1)},\nabla W)+\mathcal{R}_{aux}(\hat{x}^{(t-1)})) \\
&\eta \leftarrow \mathcal{N}(0,I) \\
&\hat{x}^{(t)} \gets \hat{x}^{(t-1)} + \lambda(t)\Delta_{\hat{x}^{(t)}} + \lambda(t)\alpha_n\eta
\end{aligned}\)
其中η是采样噪声,用于进行搜索;λ(t)是学习率;αn是缩放因子。
LPIPS(Learned Perceptual Image Patch Similarity是一种用于评估图像之间感知相似度的指标。它基于深度学习模型,特别是卷积神经网络(CNN)来模拟人类视觉系统对图像差异的感知。LPIPS旨在解决传统像素级相似度指标(如L2距离或结构相似性指数(SSIM))在评估图像质量时可能与人眼感知不一致的问题。
LPIPS通过训练一个网络来学习图像块的相似性,这个网络被训练来预测两个图像块之间的感知差异。训练数据通常包括成对的图像块,其中一些是经过轻微扰动的,而另一些则是完全不同的。网络的目标是学会区分这些差异,即使它们在像素级别上的差异可能很微小。
LPIPS的一个流行实现是使用AlexNet或VGG网络的特征提取层来计算图像块的嵌入,然后比较这些嵌入之间的距离。这种距离度量可以提供一种更接近人类视觉感知的图像相似度评估。
LPIPS在图像处理和计算机视觉领域有很多应用,例如:
- 图像超分辨率:评估重建图像与原始图像的相似度。
- 图像风格转换:评估转换后的图像是否保留了原始内容的感知特性。
- 图像去噪和修复:评估处理后图像与干净图像的接近程度。
LPIPS提供了一个更加灵活和敏感的工具,用于评估图像处理算法的质量,特别是在需要考虑人类视觉感知的情况下。
图像的峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)是衡量图像质量的一个客观标准。它常用于评估压缩算法(如JPEG、PNG)重建图像的质量,或者评估图像在传输过程中损失的情况。PSNR 以分贝(dB)为单位来度量,计算公式如下:
[ \text{PSNR} = 10 \cdot \log_{10} \left( \frac{\text{MAX}_I^2}{MSE} \right) ]
其中:
- (\text{MAX}_I) 是图像中可能的最大像素值。对于 8 位图像,这个值通常是 255。
- (MSE) 是均方误差(Mean Square Error),它是原图像 (I) 和重建图像 (K) 之间差的平方的平均值:
[ MSE = \frac{1}{M \times N} \sum_{i=0}^{M-1} \sum_{j=0}^{N-1} [I(i,j) - K(i,j)]^2 ]
这里 (M \times N) 是图像的尺寸,(I(i,j)) 和 (K(i,j)) 分别是原图像和重建图像在位置 ( (i,j) ) 的像素值。
PSNR 值越大,表示重建图像的质量越好,失真越小。通常情况下,PSNR 在 30 dB 以上,人眼就很难察觉到图像的失真;而低于 20 dB,失真就很明显了。
需要注意的是,PSNR 只能反映图像的失真程度,并不能完全代表图像的主观质量。有时候即使 PSNR 值很高,人眼仍然可能感觉到图像质量的下降,因为 PSNR 并不考虑人眼的视觉特性。因此,在评估图像质量时,通常会结合主观评价和客观指标一起来综合判断。