在看 wqs 二分前建议先去看另一篇博客——斜率优化，对凸包等知识点有所了解。

介绍

wqs 二分最初由王钦石在他的 2012 年国家集训队论文中提出，也叫"带权二分"，或者"dp凸优化"，而从 IOI 2016 的 Aliens 题目开始，这种方法开始逐步在竞赛圈中有了一定的地位。在国内我们一般称为「wqs 二分」，而在国外一般称为「Alien Trick」。

适用题型

wqs 二分的题目一般有以下特点:

• 题目内容形式为:有 \(n\) 个物品，从中选出 \(m\) 个，每个要求最后的权值最小/最大。
• 直接 dp 设 \(f[i][j]\) 表示前 \(i\) 个选出 \(j\) 个物品的话，转移是 \(f[i][j]=min_k(f[k][j-1] + Val(k,i))\),其中\(Val(k,i)\) 表示这次转移带来的权值。时间复杂度无论如何都是 \(O(n^2)\) 及以上的。
• 如果没有选 \(m\) 这个限制，那可以优化到更低复杂度,并且可以算出此时最优方案选的数的个数。
• 选的个数越多，最终权值越小/越大，即如果设 \(g(x)\),表示选 \(x\) 可以得到的最小/最大圈子，那么 \(g(x)\) 的图像构成一个凸包。

当然 wqs 二分不止应用于 DP 题，具体看例题。

解法

假设 \(g(x)\) 的图像为上凸包，要求的是最大值，不妨画一下 \(g(x)\) 的大致图像(当然其实我们是一个点都求不出来的)：

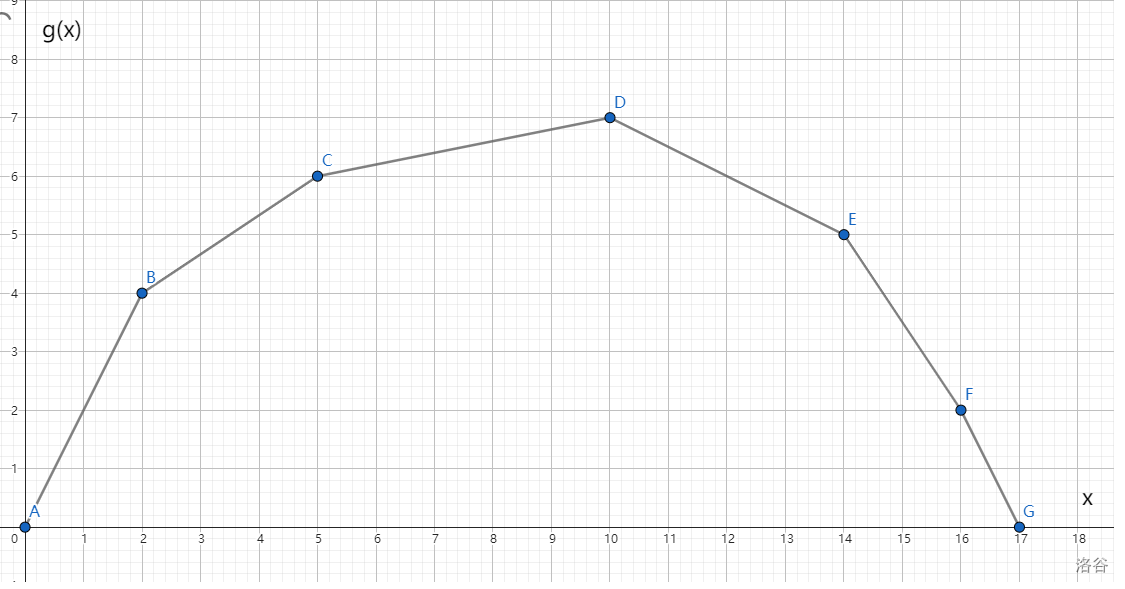
假设我们现在用一条直线 \(y=Kx+b\) 去切一个点 \((x,g(x))\)，那么可以得到 \(g(x)=Kx+b\)，即这个点的坐标也可以表示成 \((x,Kx+b)\)。
又因为上凸包有个性质，一条斜率为 \(K\) 的直线在他与这个凸包的切点处截距最大，也就是说如果我们能求出这个最大截距，并知道此时的横坐标，就能知道那个切点的具体坐标了。
因为凸包的斜率是单调的，所以随着 \(K\) 的减小，切到的 \(x\) 也越大，所以可以二分这个 \(K\),我们可以根据切点的坐标去调整 \(K\) 直到切到 \((m,g(m))\) 为止，。

现在的问题就是怎么求最大截距，因为我们压根不知道这个凸包长什么样子。
会发现 \(b = g(x)-Kx\),定义 \(h(x) = g(x)-Kx\)，如果我们能以较低的复杂度求出最大的 \(h(x)\) 以及此时的 \(x\),也就求出了我们要的东西。
考虑给 \(h(x)\) 定义一个合理的意义，不难发现他其实就是给每个物品多加了一个 \(-K\) 的权值(所以叫代权二分)，选了这个数就要 \(-K\)。
而我们要求 \(h(x)\) 的最大值是没有限制要选多少个的，所以 dp 时直接 \(f_i = max_j(f_j + Val(j,i) - K)\) 即可，比一开始那个少了一维，会更好求,具体的优化方法/求法因题目而异，在例题中会讲。
注意最后的求 \(g(x)\) 时，要记得把 \(Kx\) 加上。

关于wqs二分的实现细节也在例题中。

例题

忘情

把式子变成 $((\sum_{i=1}^n x_i)+1)^2 $,设 \(S\) 为前缀和，那么朴素的 dp 是:
设 \(f[i][j]\) 表示前 \(i\) 个数划分成 \(j\) 段的最小值，转移为 \(f[i][j]=\min_{0<=k<i}(f[k][j-1] + (S_i - S_j + 1)^2)\)。
容易证明 \((a+b+1)^2 > (a+1)^2 + (b+1)^2\),也就是说分的段数越多答案越小，即按照上面的定义 \(g(x)\) 表示分 \(x\) 段的最小值，那么 \(g(x)\) 的图像应该是一个下凸壳:

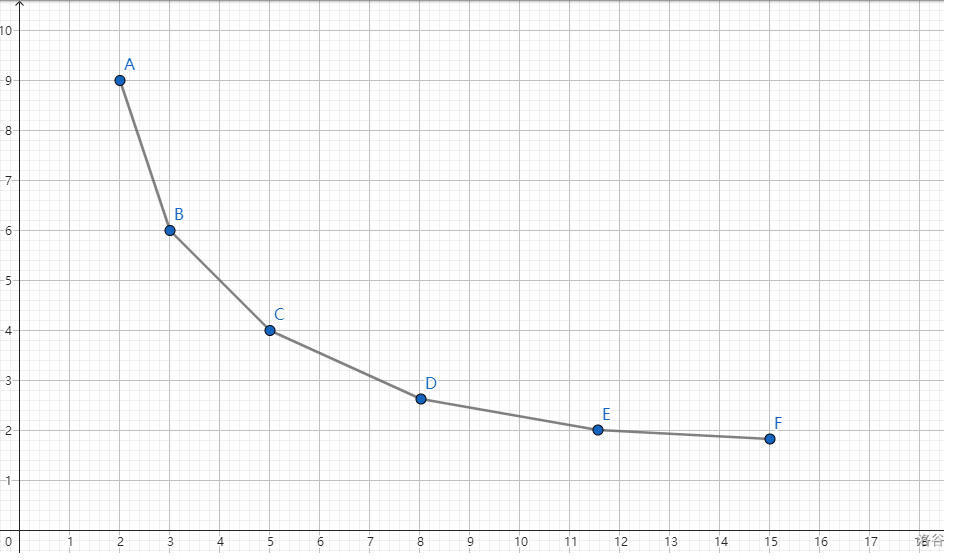
二分一个斜率 \(K\),用斜率 \(K\) 的直线去切这个凸包，那么截距 \(b=h(x)=g(x)-Kx\),因为是下凸包，所以我们要求最小截距，即把一段的权值定义成 \(((\sum xi)+1)^2 - K\),然后去掉段数限制，求最小答案。
考虑对这个新的问题 \(dp\),设 \(dp[i]\) 表示前 \(i\) 个数的最小值,\(dp[i]=\min_{0<=j<i}(dp[j] + (S[i]-S[j]+1)^2 - K)\),因为还要求此时的横坐标 \(x\)，所以还要额外记一个dp数组，转移也是显然的。
这是经典的斜率优化形式，可以用单调队列优化到 \(O(n)\),不会斜率优化的戳这里。
总时间复杂度 \(O(n \log n)\)。

wqs 二分一些实现的细节：

1. 这里因为是下凸包，所以斜率 \(K\) 是负的，但是为了方便二分时我们把他变成正的，所以 check 里 dp 变成 \(dp[i]=\min_{0<=j<i}(dp[j] + (S[i]-S[j]+1)^2 + K)\) , 原来二分要把斜率调大的就调小。
2. 注意最后凸包可能会有一段斜率为 \(0\) 的线段，即可能 \(g(m-1)=g(m)\)，那如果我们在 \(check\) 里的斜率优化dp,在 \(g\) 值相同时取的是靠左的点，那么二分写的就是: 如果返回的那个 \(x\) <=m,那就更新答案并把斜率调大(这里还认为斜率是负的，不进行 1. 的转换) ; 相反，如果我们在 \(check\) 里的斜率优化dp,在 \(g\) 值相同时取的是靠右的点，那么二分写的就是: 如果返回的那个 \(x\) >=m,那就更新答案并把斜率调小。看取的是靠左还是靠右只要看斜率优化维护凸包时写的是 >= 还是 >,> 就是取靠左的，>=就是取靠右的。

code

变量名稍有不同。

#include<bits/stdc++.h>
#define int long long 
using namespace std;
const int N=1e5+5,inf=1e18;
inline int read(){
    int w = 1, s = 0;
    char c = getchar();
    for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
    for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
    return s * w;
}

int n,m,a[N]; 
int dp[N],g[N];  //dp[i]表示前 i 个数分成若干段的最小值，g[i] 表示取到最小值分的段树 
int dq[N],l,r;
int calc(int j){  //求纵坐标 
	return dp[j]+a[j]*a[j]-2ll*a[j];
} 
void check(int mid){
	l=1,r=0;
	dp[0]=0,g[0]=0;   
	dq[++r]=0;  //放 0 不是 1，因为可以自成 1 段。 
	for(int i=1;i<=n;i++){
		while(l<r && ( calc(dq[l+1]) - calc(dq[l]) ) < (2ll * a[i] * (a[dq[l+1]] - a[dq[l]]))) l++;  //把开头斜率小于当前斜率的线段 pop 掉
		int j=dq[l];
		dp[i]=dp[j]+(a[i]-a[j]+1ll)*(a[i]-a[j]+1ll)+mid;
		g[i]=g[j]+1ll;
		while(l<r && ( calc(i) - calc(dq[r]) ) * ( a[dq[r]] - a[dq[r-1]]) < ( calc(dq[r]) - calc(dq[r-1] ) ) * ( a[i] - a[dq[r]] )) r--;  //维护凸壳
		dq[++r]=i; 
	}
}
signed main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++) a[i]=read(),a[i]+=a[i-1];
	int l=0,r=inf,mid,ans=0;   //实际上斜率是负的，但是移项之后:b=f(x)-kx,所以就干脆把 k 取成正的，这样在check里是每一段+mid,而不是-mid 
	while(l<=r){
		mid=(l+r)>>1;
		check(mid);
		if(g[n]<=m) r=mid-1,ans=mid;
		else l=mid+1; 
	}
	check(ans);
	printf("%lld\n",dp[n]-ans*m);  //这里要减掉 mid(也就是最后的 ans) 带来的贡献 
	return 0;
}