引言
在学数据结构优化dp,单调队列优化dp时都很快就懂了,四边形不等式优化dp看一看也懂了,只有斜率优化理解了一个月还不懂,最后在其他大佬和资料的帮助下成功学懂了,于是争取这篇题解在以后又不会的时候一遍就懂。
前置数学知识
1.一次函数
初中数学知识,见八年级数学课本。
2.凸包(凸壳)
- 定义:
意思是点集的边界,是一组连接相邻两点的线段斜率单调的一组点集,其中斜率单调递增的叫下凸壳,单调递减的叫上凸壳(摘自<<算法竞赛进阶指南>>)。
注意:对于正的斜率是越陡越大,对于负的斜率是越平越大
下面的是两个上凸壳:
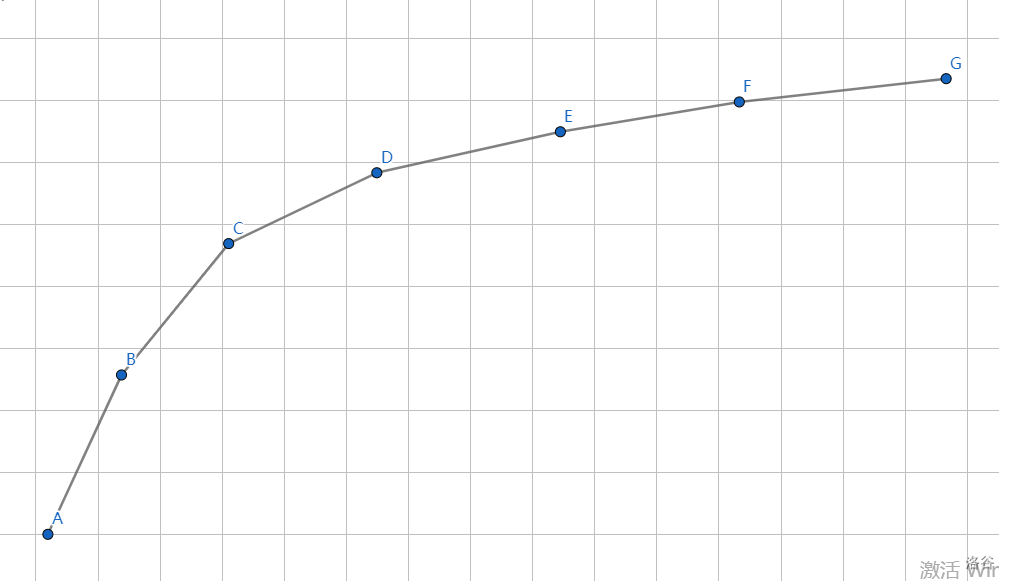
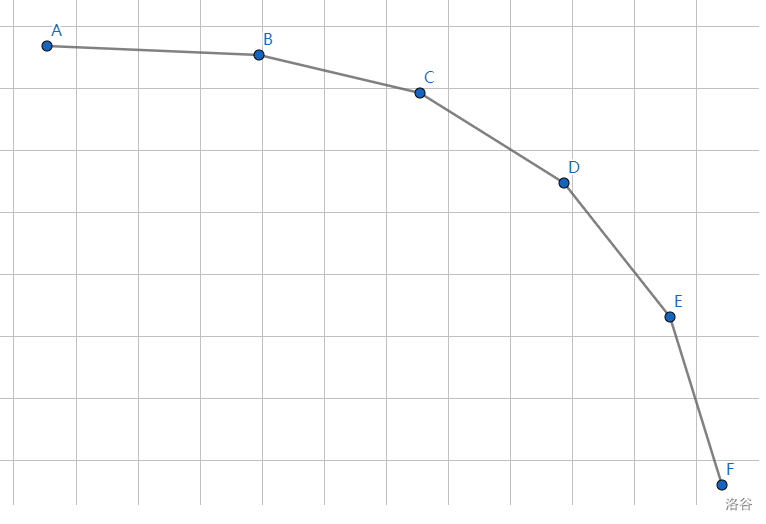
同理,下面是两个下凸壳:
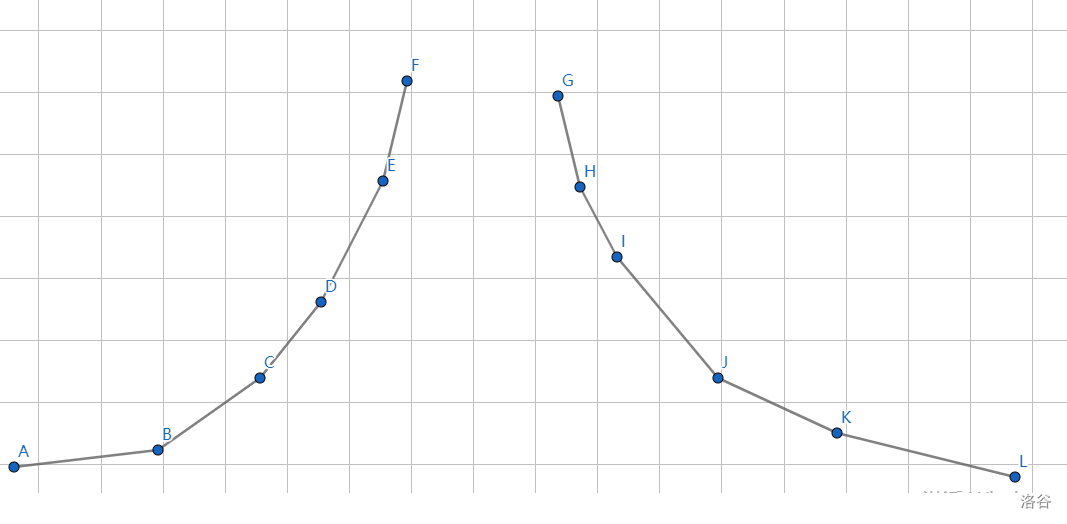
其实上凸壳还是下凸壳直接看形状就可以了。 - 性质:
我们以上凸壳为例,尝试用一条斜率固定为 \(k\) 的直线去切凸壳点集中的那些点,会得到这么多条平行线:
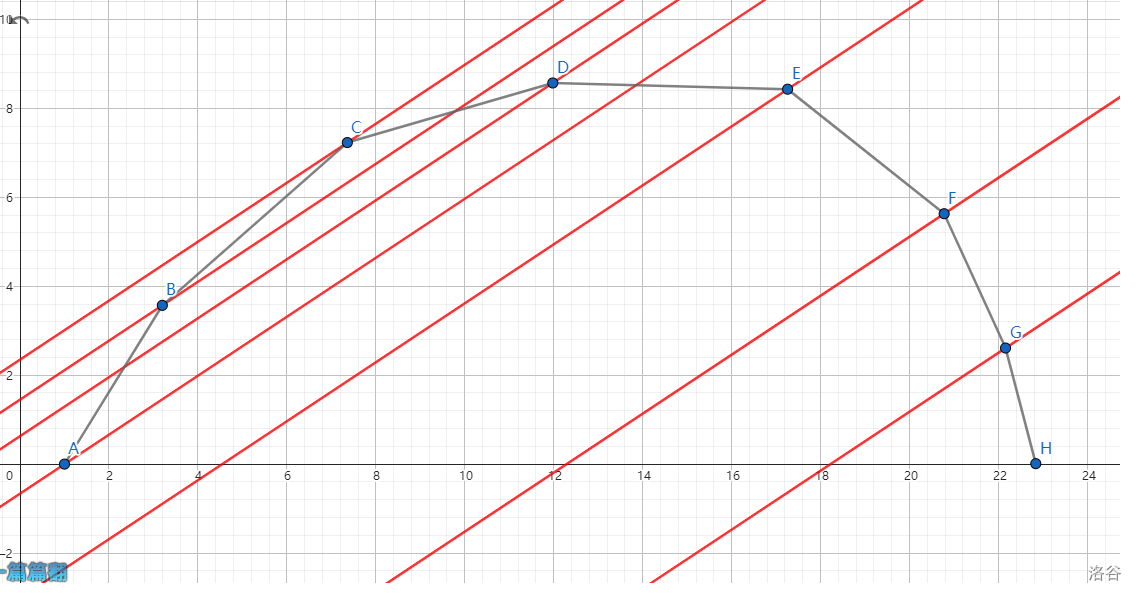
这个也是上凸壳哦。
会发现有且仅有过 \(C\) 点的那条直线与这个凸壳相切,我们称这个 \(C\) 点为斜率为 \(k\) 的直线与这个上凸壳的切点。
切点的性质是:他所确定的直线(众所周知一点和斜率可以确定一条直线)是所有直线中截距最大的。
下凸壳我们也有类似的结论,把截距最大改成最小即可。
适用场景
斜率优化用于解决dp转移方程中涉及到 \(i,j\) 的乘积项的转移,先讲它的一般形式以及解决方法再放例题。
假设我们现在有这么一个转移方程:
\[dp[i]=min_{L(i)\le j\le R(j)}(dp[j] + F1(j) + F2(i) + F3(i)\times F4(j) + A) \]其中,\(L,R,F1,F2,F3,F4\)是一些函数,\(A\) 是一个常量。
\(L,R\)的实际意义是对于每个 \(i\) 能转移到他的 \(j\) 是一段随着 \(i\) 变化而变化的区间。
\(F1,F2,F3,F4\) 则是一些关于 \(i,j\) 的表达式,因题目而异,注意 \(F1(j),F4(j)\) 只跟 \(j\) 有关,\(F2(i),F3(i)\) 只跟 \(i\) 有关。
我们可以先把与 \(j\) 无关的拉出来,放到 min 外面。
\[dp[i]=min_{L(i)\le j\le R(j)}(dp[j] + F1(j) + F3(i)\times F4(j) ) + F2(i) + A \]会变得更加美观,这样下面我们就不去管后面那一坨东西了。
然后就是斜率优化的精髓,对于一个决策点 \(j\),当用他去转移 \(i\) 时,我们可以把 min 去掉,会得到:
\[dp[i]=dp[j] + F1(j) + F3(i)\times F4(j) \]移项:
\[- F3(i)\times F4(j) + dp[i]=dp[j] + F1(j) \]我们把 \(-F3(i)\) 当作直线的斜率 \(k\),把 \(dp[i]\) 当作直线的截距 \(b\),把 \((F4(j),dp[j] + F1(j))\) 当作直角坐标系的一个点,那相当于这条直线 \(y=kx+b\) 要经过这个点。
因为我们要求的是 \(dp[i]\),也就是 \(b\), 移项得到 \(b = y - kx\),所以我们如果知道斜率和这条直线经过的点就可以知道截距了。
所以问题变成平面上有若干形如 \((F4(j),dp[j] + F1(j))\) 的点,现在要去用一条斜率为 \(k=-F3(i)\) 的直线去切这些点,求最小的截距。
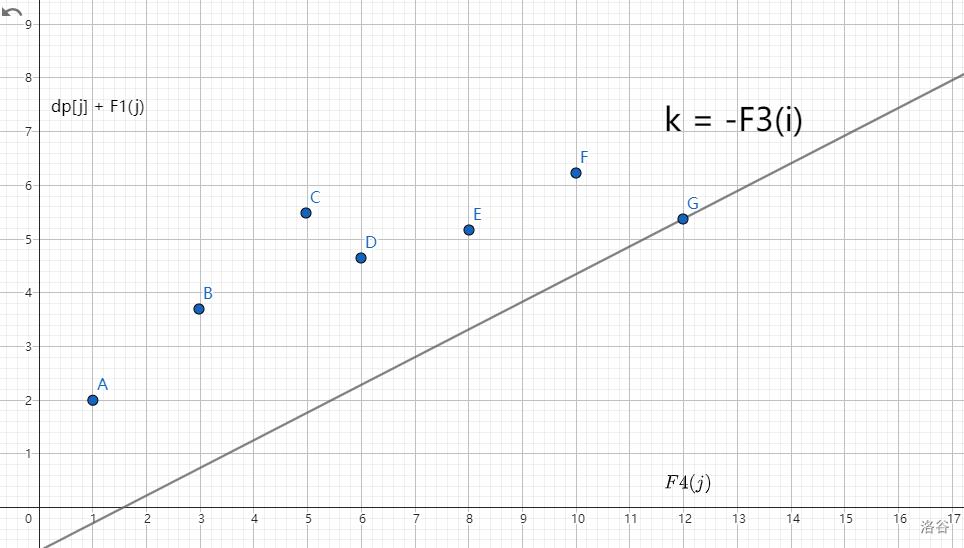
也就是需要将这条直线从下往上平移,第一个切到的点就是我们要的点,比如上图中是 \(G\) 点。
那怎么快速求出第一个切到的点呢,我们来看上图中 \(B,C,D\) 这三个点:
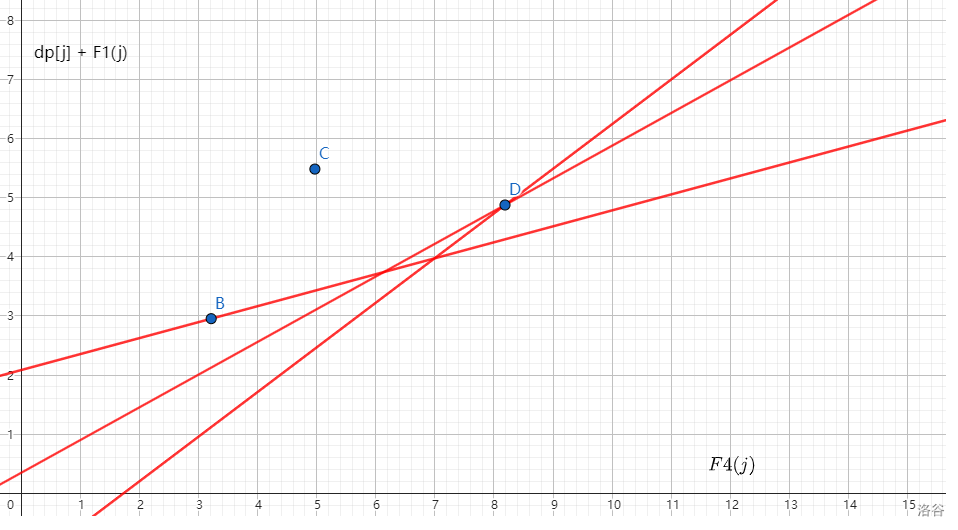
会发现不管斜率是多少,都切不到 \(C\) 点,所以这种上凸的形状中间的点是没用的,也就是说一个点 \(j_2\) 要成为决策点,假设他前面和后面的点是 \(j_1,j_3\),他的必要不充分条件是:
这个判断条件如果想简便可以直接用 long double 存,也可以十字相乘,这样可以避免精度损失带来的误判,因为斜率优化的题基本都会满足 \(j\) 的横坐标的函数 \(F4(j)\) 是单调的(不然点出现的顺序就不是按照 \(j\) 从小到大了),所以不用担心分母出现负数的情况。
也就是说我们要维护的是一个下凸壳,这可以单调栈来维护,也就是每次加入一个点就判断一下栈顶的两个点和新加的这个点是否满足上述式子(新加的点是 \(j_3\) ),不满足就不断弹栈,直到满足为止。
那维护了下凸壳之后怎么求那个切点呢?
进一步发现性质,如果一个点满足他之前线段的斜率都小于 \(k=-F3(i)\),后面线段的斜率都大于 \(k=-F3(i)\),那么这个点就是切点,如下图:
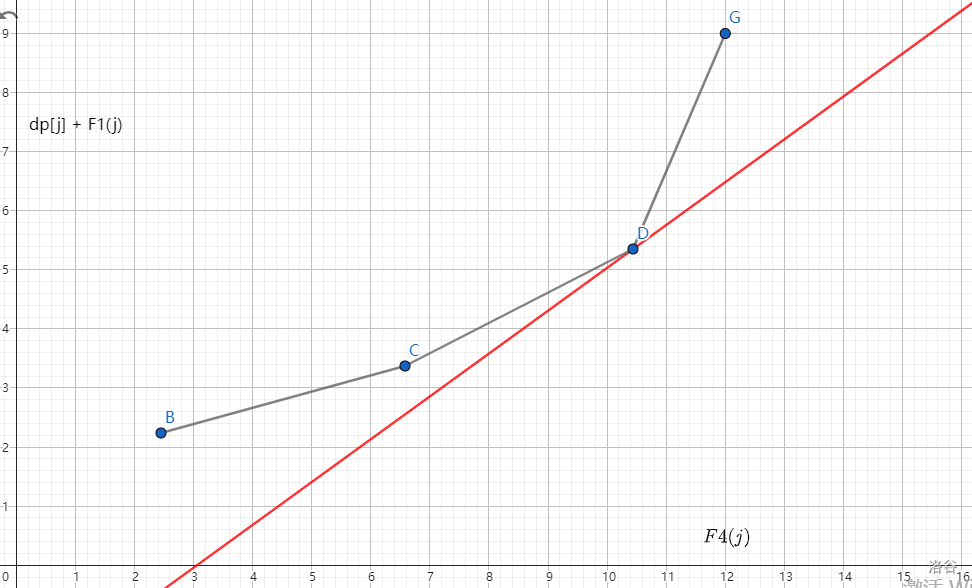
因为下凸壳的点之间的线段的斜率满足单调性,所以这显然是可以二分的(这也就意味着你的栈要手写,因为要查询栈中元素)。这是最普遍的解法,时间复杂度 \(O(n \log n)\)。
那有些时候不能带 \(log\) 怎么办呢?下面的例题会有不带 \(log\) 的解法(\(O(n)\) 解法并不是每种斜率优化的题都适用的)。
当然对于 dp 转移方程里是 max 的,维护上凸壳即可,结论类似。
例题
所有初学斜率优化的应该都是从"任务安排" 这道题开始的吧。
任务安排
弱化版是不用斜率优化的。
设 \(f[i][j]\) 表示前 \(i\) 个任务分成 \(j\) 段的最小花费。
\(f[i][j]=min_{0\le j \le i-1}(f[k][j-1] + s + (S1[i]+s\times j)\times (S2[i]-S2[k]))\)。
\(S1\) 是 \(t\) 的前缀和,\(S2\) 是 \(F\) 的前缀和。
这样是 \(O(n^3)\) 的。
回顾"我的动态规划题单2"中"关路灯"那题,
考虑将 \(s\) 的费用提前计算,只考虑当前这批任务对后面的影响,这样就可以不去记录段数 \(j\) 了。
\(f[i]=min_{0\le j \le i-1}(f[j] + S1[i]\times(S2[i]-S2[j]) + s\times (S2[n]-S2[j]))\)。
时间复杂度\(O(n^2)\)。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,s,t[N],F[N],f[N],S1[N],S2[N];
signed main(){
n=read(),s=read();
for(int i=1;i<=n;i++){
t[i]=read(),F[i]=read();
S1[i]=S1[i-1]+t[i];
S2[i]=S2[i-1]+F[i];
}
memset(f,0x3f,sizeof f);
f[0]=0;
for(int i=1;i<=n;i++){
for(int j=0;j<i;j++){
f[i]=min(f[i],f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]));
}
}
printf("%lld\n",f[n]);
return 0;
}
任务安排2
\(f[i]=min_{0\le j \le i-1}(f[j] + S1[i]\times(S2[i]-S2[j]) + s\times (S2[n]-S2[j]))\)。
按照上述所说的套路,把式子改写一下,只跟 \(j\) 有关和只跟 \(i\) 有关的拎出来:
\(f[i]=min_{0\le j \le i-1}(f[j] - (s+S1[i])\times S2[j]) + s\times S2[n] + S1[i]\times S2[i]\)。
不管后面那一坨,去掉 \(min\) 写成 \(y=kx+b\) 的形式:
\((s+S1[i])\times S2[j] + f[i] = f[j]\)。
所以就用一条斜率为 \((s+S1[i])\) 的直线去切这些形如 \((S2[j] , f[j])\) 的点。
维护出下凸壳之后,注意到因为 \(t_i\) 都是正数,所以斜率 \((s+S1[i])\) 随着 \(i\) 的增大而增大,那根据切点的判定条件,切点也是一定右移的,所以只保留斜率大于 \((s+S1[i])\) 的部分即可。
而且注意到这里的 \(L(i)\) 函数始终是 \(0\),所以就有了一下 O(n) 的做法:
- 用单调队列替换掉单调栈。
- 对于 \(i\),把队头那些斜率 \(\le (s+S1[i])\) 的线段 pop 掉,这样队头的点就是要求的切点。
- 取出队头转移。
- 加入 \(i\),并维护下凸壳。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,s,t[N],c[N],f[N],S1[N],S2[N];
int dq[N],l,r; //单调队列
int x(int j){return S2[j];} //横坐标
int y(int j){return f[j];} //纵坐标
signed main(){
n=read(),s=read();
for(int i=1;i<=n;i++){
t[i]=read(),c[i]=read();
S1[i]=S1[i-1]+t[i];
S2[i]=S2[i-1]+c[i];
}
memset(f,0x3f,sizeof f);
f[0]=0;
l=1,r=0; //初始化空的单调队列
dq[++r]=0;
for(int i=1;i<=n;i++){
while( l<r && ( y(dq[l+1]) - y(dq[l]) ) <= (s + S1[i]) * ( x(dq[l+1]) - x(dq[l]) ) ) l++; //注意是 l<r 而不是 l<=r,因为起码要有两个点才是线段
int j=dq[l];
f[i]=f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]); //这里就用原来的式子就好了,新的那个太大便了
while( l<r && ( y(dq[r]) - y(dq[r-1]) ) * ( x(i) - x(dq[r]) ) >= ( y(i) - y(dq[r]) ) * ( x(dq[r]) - x(dq[r-1]) ) ) r--; //维护凸壳
dq[++r]=i;
}
printf("%lld\n",f[n]);
return 0;
}
[SDOI2012] 任务安排
题面都是一样的。
这里 \(t_i\) 可能是负数,所以 \((s+S1[i])\) 不一定单调。
所以求切点要二分,这里还是用的单调队列,其实单调栈也可以。
时间复杂度 O(n log n)。
要注意的是,这里 \(c_i\) 可以等于 \(0\),也就是说也就是会出现横坐标相同的两个点,那么有可能出现原先的斜率是 \(inf\)(即与 \(x\) 轴垂直,但是后面那个在前面那个上面),加进来一个后变成 \(-inf\)(加进来的在原来队尾的下面),但它们的斜率在比较时是一样,如果不把前面那个弹掉,就不满足斜率单调递增了,所以在维护下凸壳时,\(=\) 的情况也要把队尾弹掉(代码中也有注释)。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=3e5+5;
inline int read(){
int w = 1, s = 0;
char c = getchar();
for (; c < '0' || c > '9'; w *= (c == '-') ? -1 : 1, c = getchar());
for (; c >= '0' && c <= '9'; s = 10 * s + (c - '0'), c = getchar());
return s * w;
}
int n,s,t[N],c[N],f[N],S1[N],S2[N];
int dq[N],l,r; //单调队列
int x(int j){return S2[j];} //横坐标
int y(int j){return f[j];} //纵坐标
int Binary_search(int K){
int L=l,R=r,mid,res=r; //二分找第一个满足它后面的线段的斜率比 s+S1[i] 大的点y
while(L<=R){
mid=(L+R)>>1;
if(mid<r && y(dq[mid+1]) - y(dq[mid]) > K * ( x(dq[mid+1]) - x(dq[mid]) )) R=mid-1,res=mid;
else L=mid+1;
}
return dq[res];
}
signed main(){
n=read(),s=read();
for(int i=1;i<=n;i++){
t[i]=read(),c[i]=read();
S1[i]=S1[i-1]+t[i];
S2[i]=S2[i-1]+c[i];
}
memset(f,0x3f,sizeof f);
f[0]=0;
l=1,r=0; //初始化空的单调队列
dq[++r]=0;
for(int i=1;i<=n;i++){
int j=Binary_search(s+S1[i]);
f[i]=f[j] + S1[i]*(S2[i]-S2[j]) + s*(S2[n]-S2[j]);
while( l<r && ( y(dq[r]) - y(dq[r-1]) ) * ( x(i) - x(dq[r]) ) >= ( y(i) - y(dq[r]) ) * ( x(dq[r]) - x(dq[r-1]) ) ) r--; //维护凸壳
/*
这边取等号是因为 ti 可以=0,也就是会出现横坐标相同的两个点,那么有可能出现原先的斜率是 inf(即与 x 轴垂直,但是后面那个在前面那个上面),
加进来一个后变成 -inf,但它们的斜率表示出来是一样,如果不把前面那个弹掉,就不满足斜率单调递增了。
*/
dq[++r]=i;
}
printf("%lld\n",f[n]);
return 0;
}
拓展
如果对于任务安排这题,\(Ti,Ci\) 都可能是负数怎么办?
这个时候就要更高级的李超树或者平衡树了,这里还不会,就先挖个坑。