首页 > 其他分享 >题解：P7952 [✗✓OI R1] 天动万象

题解：P7952 [✗✓OI R1] 天动万象

时间：2024-08-25 21:06:26浏览次数：8  
标签：siz P7952 R1 1v 题解 tr uint32 权值 节点

提供一种和第一篇题解不同的理解思路。

题目分析

看到操作 \(1\)：拿 dfs 序水水就行了。

看到操作 \(2\)：？？？

特殊情况

我们考虑一下特殊情况下操作 \(2\) 怎么处理。

假如这棵树是一条链。

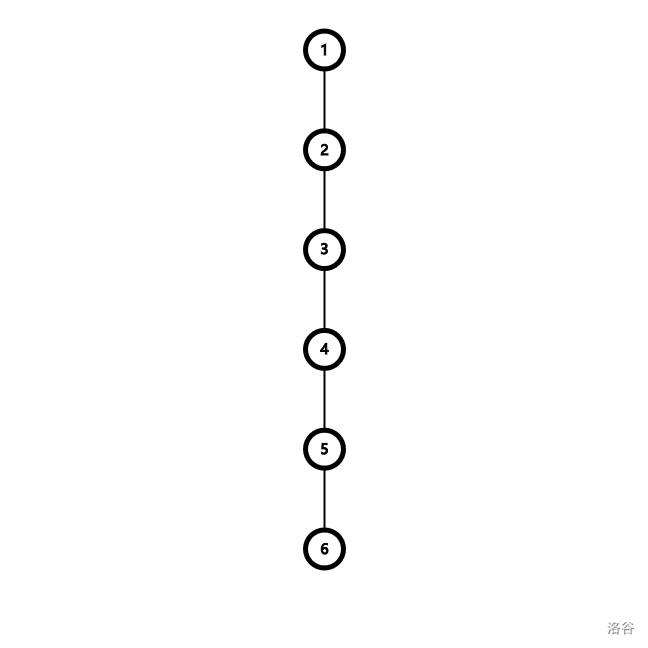
设从根到叶节点权值如下：（随便赋的）

节点编号 1 2 3 4 5 6
权值 1 2 3 4 5 6

如果我们对 \(2\) 号节点执行操作 \(2\)，权值就变成这样：

节点编号 1 2 3 4 5 6
权值 1 3 4 5 6 0

再对 \(1\) 号节点执行操作 \(2\)，权值就变成这样：

节点编号 1 2 3 4 5 6
权值 3 4 5 6 0 0

发现在链的情况下，直接将 \([p,p+\textrm{size}(p)-1]\) 的区间向左平移一位，首位舍弃，末位补零即可。

这样打一棵 FHQ Treap 维护区间最大值就行了。

一般情况

序列处理

那要是它不是一条链呢？

感觉刚刚的做法比较好用，尝试往树上套。

例如这棵树：

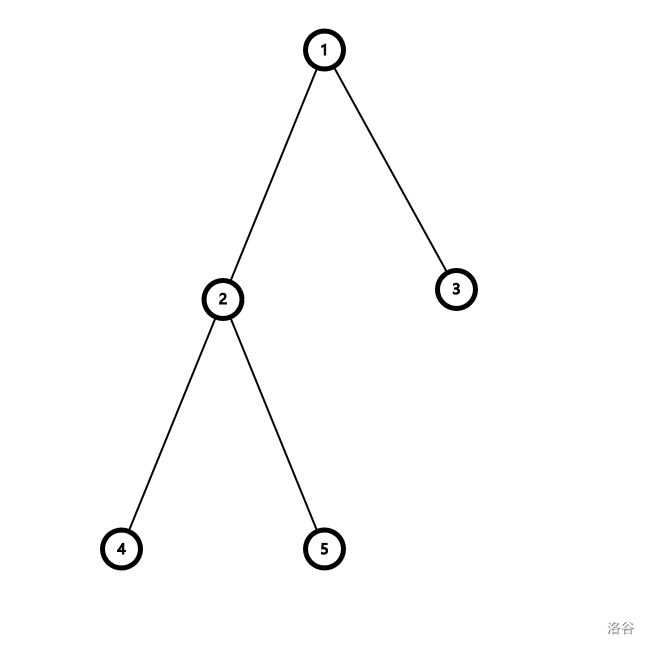
设从根到叶节点权值如下：

节点编号 1 2 3 4 5
权值 1 2 3 4 5

发现此时单纯的平移无法满足条件。

考虑给有多个儿子的节点开几个虚拟节点。

保证对于任意非根非虚拟节点，在序列上它的前一位是它的父亲。

同时保证一个子树中的节点在序列上是连续的。（和树链剖分一样）

所以就变成这样：（v 表示虚拟节点，r 表示普通节点）

1r 2r 4r 2v 5r 1v 3r
1 2 4 0 5 0 3

发现这就是在回溯时不记录该节点的欧拉序。

如果我们对 \(1\) 号节点执行操作 \(2\)，权值就变成这样：

1r 2r 4r 2v 5r 1v 3r
2 4 0 5 0 3 0

发现满足了题意，只要每次将虚拟节点上的权值转移回根节点即可。

权值转移

考虑朴素转移，记录每个节点的所有虚拟节点，每次枚举子树内的非叶节点，暴力加。

发现一次操作时间复杂度为 \(O(n)\)。（链的情况）

评价是不如暴力。

我们很容易发现，对于任意子树，虚拟节点的个数就是叶节点个数减 \(1\)。

考虑从叶节点更新虚拟节点。

我们为每个节点分配一个它负责更新的节点。

1r 2r 4r 2v 5r 1v 3r
- - - - 2v - 1v

每次修改的时候枚举叶节点，将其对应的虚拟节点的权值更新到普通节点上即可。

为了保证时间复杂度，每次更新后应动态维护叶节点，删去原本的。

现在要解决两个问题：

  1. 如何为每个节点分配它负责更新的节点？
  2. 如何动态维护叶节点集合？

对于第一个问题，首先我们知道，对于一条链上的节点，它们负责更新的节点应该是同一个。

比如下图：

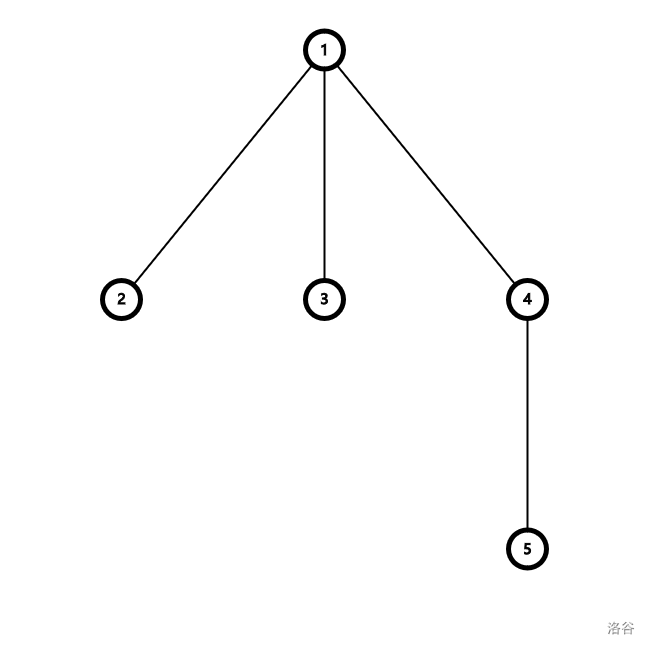
1r 2r 1v-1 3r 1v-2 4r 5r
- - - 1v-1 - 1v-2 1v-2

4r 节点和 5r 节点应维护同一信息，否则在操作后删去 5r 后会导致没有节点更新 1v-2 节点。

这一部分可以利用链剖分的方式进行。

出于一些神奇的原因，我的代码只有重链剖分能过，望各位大佬告诉我原因。

再考虑如何维护叶节点集合。

注意：这里的叶节点包括所有用于更新节点的点，有的点可能不是叶子。

考虑开一棵平衡树来维护，其中存储叶节点在序列上的编号。

每次枚举 \([\textrm{begin}(p),\textrm{end}(p)]\) 间的叶节点。

  • 该节点是真正的叶节点，那么更新完后删除自己，尝试将父节点加入。
  • 该节点不是真正的叶节点，那么更新完就不用管了。

父节点加入集合有两种情况：

  • 该节点和父节点在同一条链上，为了保证正常更新，所以将父节点加入。
  • 删去该节点后父节点成了叶子。

结束。

Code

这份代码为了卡常整体十分丑陋。

我把指针 FHQ 换成了数组版的，并且把结构体给丢了，换成命名空间。

还有极为混乱的宏定义。

我在卡的时候只要能过编译就行。

#include<bits/stdc++.h>
using namespace std;
#define maxn 1000006
mt19937 rnd(time(0));

namespace s_tr
{
    struct node
    {
        uint64_t v=0;
        uint32_t id=0;
        int siz=1;
        uint32_t lc=0, rc=0;
        uint64_t mx=0;
        node(uint64_t va, uint32_t d): v(va), id(d) {mx=v;}
        node() {}
    }tr[maxn<<1];

    #define siz(x) (x?tr[x].siz:0)

    int push_up(uint32_t x)
    {
        tr[x].siz=1+siz(tr[x].lc)+siz(tr[x].rc);
        tr[x].mx=max({tr[x].v, tr[tr[x].lc].mx, tr[tr[x].rc].mx});
        return x;
    }

    int rt=0, cnt=0;

    int new_node(uint64_t v) 
    {
        tr[++cnt]=node(v, rnd());
        return cnt;
    }

    void split(uint32_t x, int s, uint32_t &l, uint32_t &r)
    {
        if(!x) return l=r=0, void();
        if(siz(tr[x].lc)<s) l=x, split(tr[x].rc, s-siz(tr[x].lc)-1, tr[x].rc, r);
        else             r=x, split(tr[x].lc, s, l, tr[x].lc);
        push_up(x);
    }

    uint32_t merge(uint32_t x, uint32_t y)
    {
        if(!x||!y) return x?x:y;
        if(tr[x].id<tr[y].id)
        {
            tr[x].rc=merge(tr[x].rc, y);
            return push_up(x);
        }
        else
        {
            tr[y].lc=merge(x, tr[y].lc);
            return push_up(y);
        }
    }

    void push_back(int v) {rt=merge(rt, new_node(v));}

    uint64_t max_element(int l, int r)
    {
        uint32_t a, b, c;
        split(rt, l-1, a, b);
        split(b, r-l+1, b, c);
        uint64_t ret=tr[b].mx;
        rt=merge(a, merge(b, c));
        return ret;
    }

    void modify(int p, uint64_t v)
    {
        uint32_t a, b, c;
        split(rt, p-1, a, b);
        split(b, 1, b, c);
        tr[b].mx=tr[b].v=v;
        rt=merge(a, merge(b, c));
    }
    
    void accumulate(int p, uint64_t v)
    {
        uint32_t a, b, c;
        split(rt, p-1, a, b);
        split(b, 1, b, c);
        tr[b].mx=tr[b].v=v+tr[b].v;
        rt=merge(a, merge(b, c));
    }

    int64_t get(int k)
    {
        uint32_t p=rt;
        while(p)
        {
            uint32_t sz=siz(tr[p].lc);
            if(k<=sz) p=tr[p].lc;
            else if(k<=sz+1) return tr[p].v;
            else {k-=sz+1, p=tr[p].rc;}
        }
        return 0;
    }
}

int val[maxn];
vector<int> e[maxn];
int fa[maxn], vis[maxn<<1];

vector<int> ins;

namespace tr
{
    struct node
    {
        uint64_t v=0;
        uint32_t id=0;
        int siz=1;
        uint32_t lc=0, rc=0;
        node(uint64_t va, uint32_t d): v(va), id(d) {}
        node() {}
    }tr[maxn<<1];

    #define siz(x) (x?tr[x].siz:0)

    int push_up(uint32_t x)
    {
        tr[x].siz=1+siz(tr[x].lc)+siz(tr[x].rc);
        return x;
    }

    int rt=0, cnt=0;

    int new_node(uint64_t v) 
    {
        tr[++cnt]=node(v, rnd());
        return cnt;
    }

    void split(uint32_t x, int v, uint32_t &l, uint32_t &r)
    {
        if(!x) return l=r=0, void();
        if(tr[x].v<=v) l=x, split(tr[x].rc, v, tr[x].rc, r);
        else           r=x, split(tr[x].lc, v, l, tr[x].lc);
        push_up(x);
    }

    uint32_t merge(uint32_t x, uint32_t y)
    {
        if(!x||!y) return x?x:y;
        if(tr[x].id<tr[y].id)
        {
            tr[x].rc=merge(tr[x].rc, y);
            return push_up(x);
        }
        else
        {
            tr[y].lc=merge(x, tr[y].lc);
            return push_up(y);
        }
    }

    void insert(int v)
    {
        uint32_t x, y;
        split(rt, v, x, y);
        rt=merge(merge(x, new_node(v)), y);
    }

    void erase(int v)
    {
        uint32_t l, r, x, y;
        split(rt, v, l, r);
        split(l, v-1, x, y);
        l=merge(tr[y].lc, tr[y].rc);
        rt=merge(merge(x, l), r);
    }
}

int son[maxn], siz[maxn], deg[maxn];
int st[maxn], ed[maxn], top[maxn], dic[maxn<<1];

vector<uint32_t> con;
void work(uint32_t xp)
{
    if(!xp) return;
    work(tr::tr[xp].lc);
    con.emplace_back(tr::tr[xp].v);
    work(tr::tr[xp].rc);
}

void dfs1(int u)
{
    siz[u]=1;
    for(auto v:e[u])
    {
        dfs1(v);
        siz[u]+=siz[v];
        if(siz[v]>siz[son[u]])
            son[u]=v;
    }
}

void dfs2(int u, int tx)
{
    dic[st[u]=++*dic]=u;
    top[u]=tx;
    deg[u]=e[u].size();
    s_tr::push_back(val[u]);
    if(son[u]) dfs2(son[u], tx);
    for(auto v:e[u])
        if(v!=son[u])
        {
            s_tr::push_back(0);
            dic[++*dic]=u;
            dfs2(v, *dic);
        }
    ed[u]=*dic;
    if(!son[u]) 
        tr::insert(st[u]), 
        vis[st[u]]=1;
}

#undef siz
#define siz 100000000
char buf[siz],*p1=buf,*p2=buf,obuf[siz],*p3=obuf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,siz,stdin),p1==p2)?EOF:*p1++)
#define putchar(x) (p3-obuf<siz)?(*p3++=x):(fwrite(obuf,p3-obuf,1,stdout),p3=obuf,*p3++=x)
#define flush() fwrite(obuf,p3-obuf,1,stdout),p3=obuf
template<typename T>inline void read(T &x){char c=getchar();x=0;for(;!isdigit(c);c=getchar());for(;isdigit(c);c=getchar()) x=((x<<3)+(x<<1)+(c^48));}

int main()
{
    int n, q;
    read(n), read(q);
    for(int i=1;i<=n;i++) read(val[i]);
    for(int i=2;i<=n;i++) read(fa[i]), e[fa[i]].emplace_back(i);
    dfs1(1);
    dfs2(1, 1);
    while(q--)
    {
        int op, u;
        read(op), read(u);
        if(op==1) printf("%lld\n", s_tr::max_element(st[u], ed[u]));
        else
        {
            uint32_t a, b, c, d;
            s_tr::split(s_tr::rt, st[u]-1, a, b);
            s_tr::split(b, ed[u]-st[u]+1, b, d);
            if(!s_tr::tr[b].mx) 
            {
                s_tr::rt=s_tr::merge(a, s_tr::merge(b, d));
                continue;
            }
            s_tr::split(b, 1, b, c);
            s_tr::tr[b].v=s_tr::tr[b].mx=0;
            s_tr::rt=s_tr::merge(a, s_tr::merge(c, s_tr::merge(b, d)));
            tr::split(tr::rt, st[u]-1, a, b);
            tr::split(b, ed[u], b, c);
            con.clear();
            work(b);
            for(auto xt:con)
            {
                int p=dic[xt];
                int t=top[p];
                if(t!=st[dic[t]])
                {
                    uint64_t x=s_tr::get(t);
                    if(x)
                    {
                        s_tr::modify(t, 0);
                        s_tr::accumulate(st[dic[t]], x);
                    }
                }
                if(!deg[p])
                {
                    if((!--deg[fa[p]]||top[fa[p]]==t)&&!vis[st[fa[p]]]) 
                        ins.emplace_back(st[fa[p]]), vis[st[fa[p]]]=1;
                }
                else ins.emplace_back(xt);
            }
            tr::rt=tr::merge(a, c);
            for(auto v:ins) tr::insert(v);
            ins.clear();
        }
    }
    flush();
}

标签：siz,P7952,R1,1v,题解,tr,uint32,权值,节点
From： https://www.cnblogs.com/redacted-area/p/18379555

相关文章

  • 题解：CF1995C Squaring
    题意给定序列\(a\)，每次操作可以使\(a_i\getsa_i^2\)，求使\(a\)不降的最少操作次数。分析因为\(1^k=1\)，所以无解的情况只有\(\exist\a_i=1\)且\(\exist\j\in[1,i),a_j>1\)。在有解的情况下，假设对\(a_{i-1}\)操作\({k_{i-1}}\)次，对\(a_i\)操作\({k_i}\)次。......
  • 题解：UVA1479 Graph and Queries
    分析先看删边操作。由于并不保证是森林，所以我们没有好的方法来在线维护删边相关的操作。所以，我们可以套路地把询问离线，然后倒着操作。删边变成加边。需要注意的是权值的修改，记录时要把当前权值和修改的权值反过来。然后我们发现这个操作很经典，维护方式和[HNOI2012]永无乡......
  • 题解：P7475 「C.E.L.U-02」简易输入法
    题意给定词典\(\text{U}\)，每次询问读入一个字符串\(s\)，以及一个整数\(x\)对于这个字符串有以下几种情形：设\(s_i\in\text{U}\)且\(s\)为\(s_i\)的前缀的个数为\(a\)。当\(a\gex\)时，请输出按照以输出次数从大到小为第一关键字，以字典序为第二关键字排序后的第\(x......
  • 题解：P7401 [COCI2020-2021#5] Planine
    题意现有一座上下起伏的山。它可以抽象为一个包含\(n\)（\(n\)为奇数）个点\((x_i,y_i)\)以及\((x_1,-\inf)\)与\((x_n,-\inf)\)的多边形。对于所有满足\(i\neq1\)，\(i\neqn\)，\(i\bmod2=1\)的整数\(i\)，\((x_i,y_i)\)都是山谷。现要放置若干个高度为\(h\)的点光......
  • 题解：SP1182 SORTBIT - Sorted bit squence
    题意将区间\([m,n]\)的所有整数按照其二进制位表示的数中\(1\)的数量从小到大排序。如果\(1\)的数量相同，则按照数的大小排序。求序列中第\(k\)个数。其中，负数使用补码来表示：一个负数的二进制数与其相反数的二进制数之和恰好等于\(2^{32}\)。分析考虑用uint32_t存......
  • 题解：P3266 [JLOI2015] 骗我呢
    题意有一个\(n\timesm\)的数组\(x_{i,j}(1\lei\len,1\lej\lem)\)，满足：\(x_{i,j}\in[0,m]\)\(\foralli\in[1,n],\forallj\in[1,m),x_{i,j}<x_{i,j+1}\)\(\foralli\in(1,n],\forallj\in[1,m),x_{i,j}<x_{i-1,j+1}\)......
  • 题解：CF70D Professor's task
    题意实现以下两种操作:往点集\(S\)中添加一个点\((x,y)\)。询问点\((x,y)\)是否在点集\(S\)的凸包中。分析动态凸包板子。建议先完成P2521[HAOI2011]防线修建。上题维护的是上半个凸包，本题维护上下两个。将凸包中的点按\(x\)排序，通过\((x,y)\)前驱......
  • 题解：P2521 [HAOI2011] 防线修建
    题意给定若干个点，实现下列操作：删除一个点。查询上凸包的周长。分析建议先完成【模板】二维凸包。对于这个删除操作，我们没有好的方法去在线维护它。考虑离线询问。这样删除操作就变成了插入操作。插入一个新点有如下两种情况：新点在凸包内。新点在凸包外。我们回忆......
  • 题解：CF235C Cyclical Quest
    题意给定一个主串\(S\)和\(n\)个询问串，求每个询问串的所有循环同构在主串中出现的次数总和。分析后缀自动机好题。循环同构的过程可以看作从该串的头部删除一个字符，并在尾部加入一个字符。在后缀自动机上，跳parent树的过程就相当于删除头部的若干个字符。所以我们可......
  • 7z解压crc错误_7-Zip - 常见问题解答
    7z解压crc错误_7-Zip-常见问题解答7z解压crc错误_7-Zip-常见问题解答1.引言1.17-Zip简介1.2CRC错误概述2.7z文件和CRC错误2.1什么是7z文件2.2CRC错误的定义2.3CRC错误对文件的影响3.常见原因分析3.1文件传输过程中的错误3.2存储介质的损坏3.3不兼容的压......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99