题意

现有一座上下起伏的山。它可以抽象为一个包含 \(n\)（\(n\) 为奇数）个点 \((x_i,y_i)\) 以及 \((x_1,-\inf)\) 与 \((x_n,-\inf)\) 的多边形。

对于所有满足 \(i \neq 1\)，\(i \neq n\)，\(i \bmod 2=1\) 的整数 \(i\)，\((x_i,y_i)\) 都是山谷。

现要放置若干个高度为 \(h\) 的点光源，使得所有的山谷都被照亮，即点光源与山谷的连线不经过山的内部。

求所需点光源的最少数量。

分析

考虑对每个山谷处理出能照亮它的点集。

比如对于如下山谷：

处理出第 \(2\) 个山谷能照亮它的点集，显然是一条在直线 \(y=h\) 上的线段：

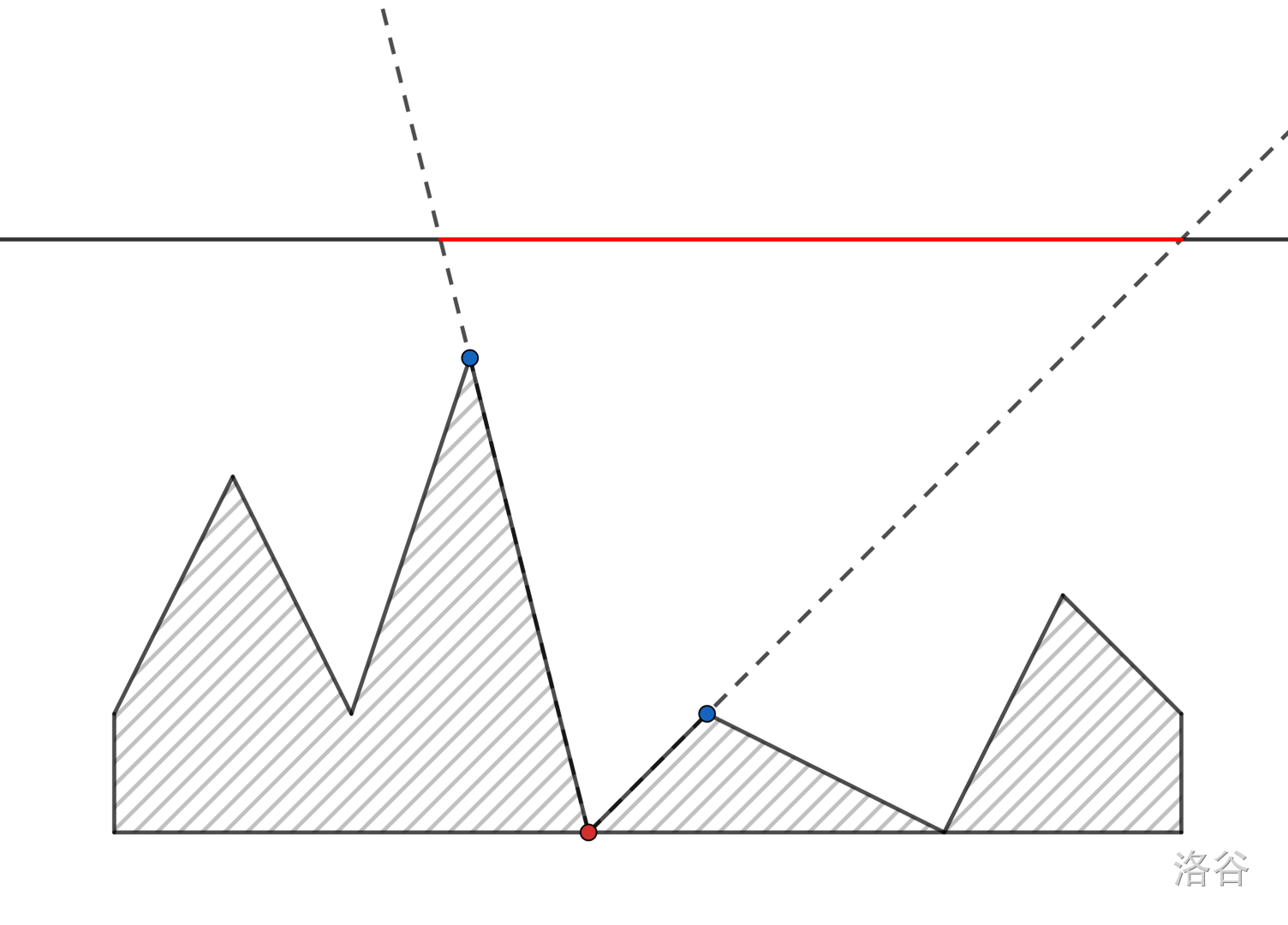
对于第 \(2\) 个山谷而言，能照亮它的点集只受前后紧邻点的限制。

但是第 \(3\) 个山谷就有点区别了：

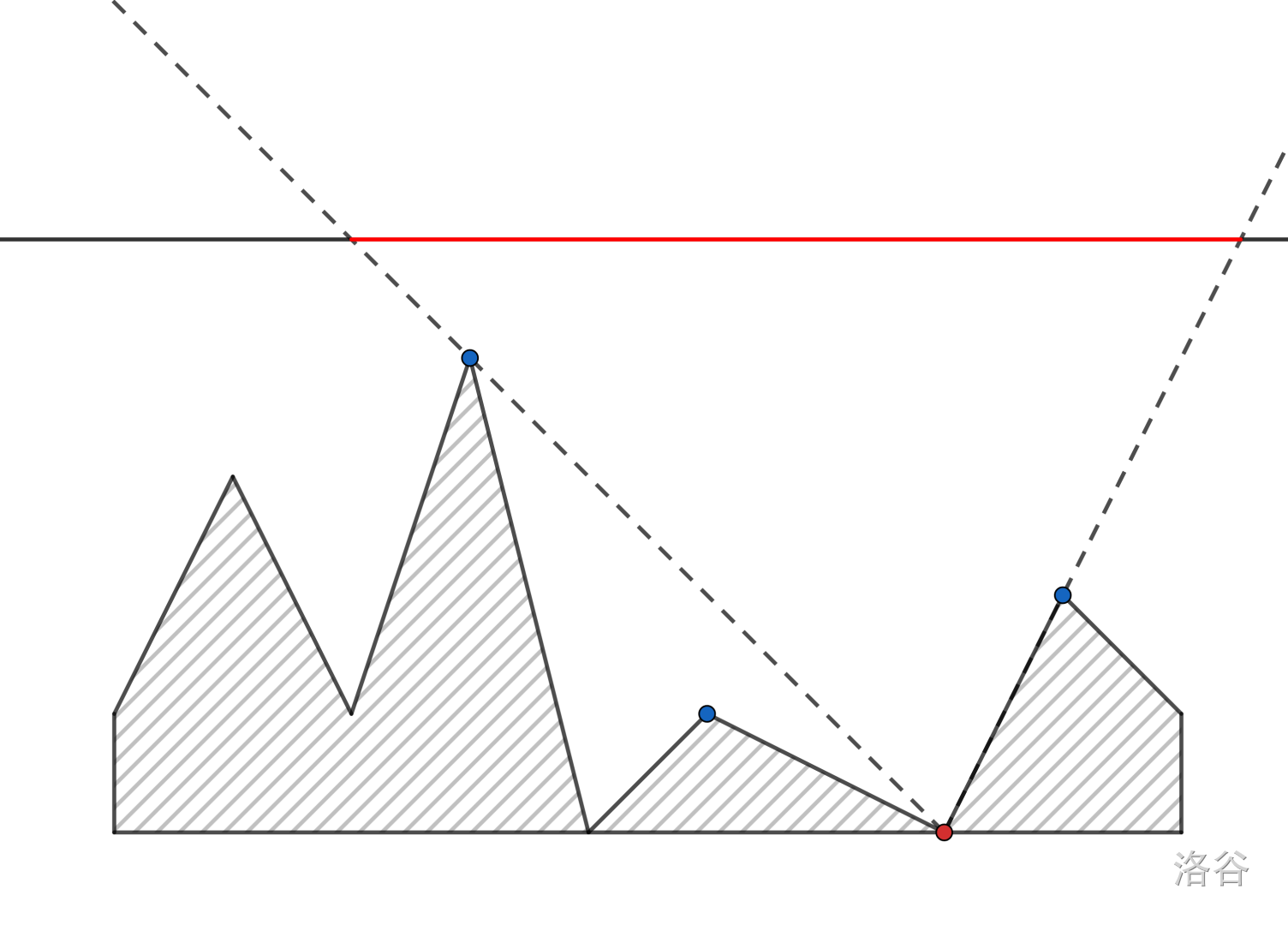
我们发现它还受另外的点的限制。

考虑维护一个凸包，如下图：

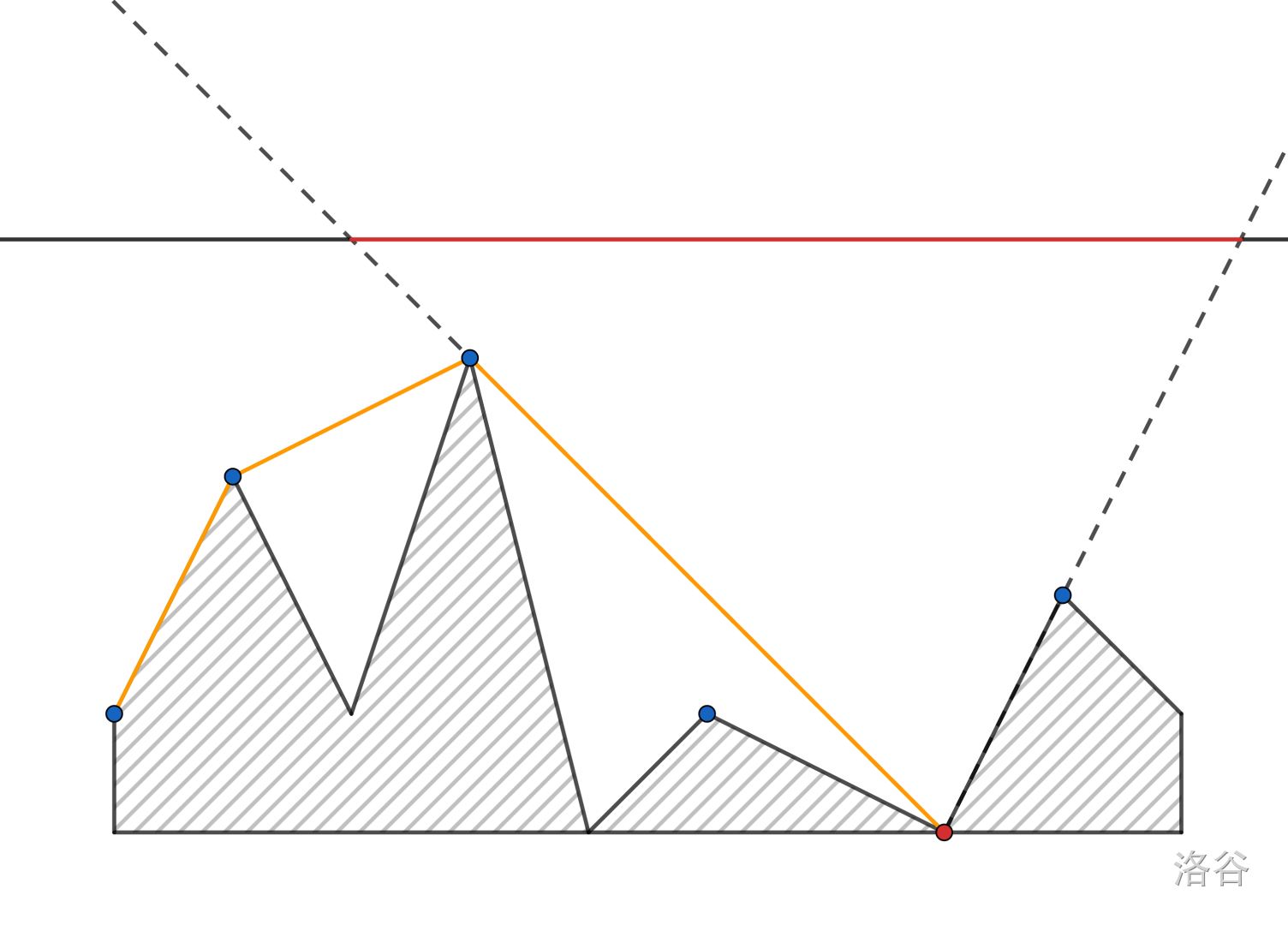
点集所受的限制就是凸包中最后一条边。

所以我们正向扫一遍，维护一个凸包，再反向扫一遍，维护另一个凸包即可。

时间复杂度 \(O(n)\)。

现在我们得到了若干个区间，我们需要选取若干个点，使得每个区间内至少存在一个点，并最小化点的个数。

这是一个比较经典的贪心问题。

考虑按右端点从小到大排序，每次选取右端点最小的区间，并去除所有与该区间相交的区间。

答案即为选取的次数。

正确性显然。

Code

#include<bits/stdc++.h>
using namespace std;
#define maxn 1000006
typedef long double f64_t;

struct dot{int x, y;}ds[maxn];
f64_t slope(dot a, dot b) {return (f64_t)(a.y-b.y)/(a.x-b.x);}

struct segement
{
    f64_t l, r;
    segement(f64_t x=0, f64_t y=0): l(x), r(y) {}
    friend bool operator<(segement a, segement b) {return a.r<b.r; }
}seg[maxn];

vector<int> s;
#define chk(x) ((x)!=1&&(x)!=n&&((x)&1))
f64_t back() {return slope(ds[*s.rbegin()], ds[*(s.rbegin()+1)]);}

int main()
{
    int n, h;
    cin>>n>>h;
    for(int i=1;i<=n;i++) cin>>ds[i].x>>ds[i].y;
    for(int i=1;i<=n;i++)
    {
        while(s.size()>1&&back()<=slope(ds[s.back()], ds[i])) 
            s.pop_back();
        s.emplace_back(i);
        if(chk(i)) 
        {
            f64_t k=back();
            f64_t b=ds[i].y-k*ds[i].x;
            seg[i].l=(h-b)/k;
        }
    }
    s.clear();
    for(int i=n;i;i--)
    {
        while(s.size()>1&&back()>=slope(ds[s.back()], ds[i])) 
            s.pop_back();
        s.emplace_back(i);
        if(chk(i)) 
        {
            f64_t k=back();
            f64_t b=ds[i].y-k*ds[i].x;
            seg[i].r=(h-b)/k;
        }
    }
    vector<segement> vc;
    for(int i=3;i<n;i+=2) 
        vc.emplace_back(seg[i]);
    sort(vc.begin(), vc.end());
    f64_t mxr=-1e18;
    int ans=0;
    for(auto [l, r]:vc) 
        if(l-1e-8>mxr) mxr=r, ans++;
    cout<<ans;
}