1 Miller-Rabin 算法

1.1 引入

Miller-Rabin 的主要作用就是判断一个较大的数是不是质数。

那么根据基础数论中提到过的试除法，我们知道朴素去判断一个数是否是质数的复杂度是 \(O(\sqrt n)\) 的，在 \(n\ge 10^{18}\) 的时候就十分不优了。

而 Miller-Rabin 则是基于费马小定理进行的素性测试，所以首先我们需要知道费马小定理是什么：

当 \(p\) 为质数时，对于任意整数 \(a\)，会有 \(a^{p-1}\equiv 1\pmod p\)。

那么如果对于所有的 \(a\)，都有 \(a^{p-1}\equiv 1\pmod p\)，是否说明 \(p\) 一定是质数呢？事实上不一定，但是其正确率仍然是有的。那我们如果可以利用这种随机性，把正确率不断提高逼近 \(100\%\)，是否说明这样的做法也有一定的可取性？

事实上本文介绍的两个算法看上去都是基于随机的，但是都有很高的正确率。

1.2 算法实现

在了解 Miller-Rabin 的实现过程之前，需要了解二次探测定理。

1.2.1 二次探测定理

二次探测定理：若 \(p\) 为素数，且 \(a^2\equiv 1\pmod p\)，那么一定有 \(a\equiv \pm1\pmod p\)。

证明：

\(\because a^2\equiv 1\pmod p\)

\(\therefore a^2-1\equiv 0\pmod p\)。

\(\therefore (a+1)(a-1)\equiv 0\pmod p\)。

\(\therefore\) \(a+1\equiv 0\pmod p\) 或 \(a-1\equiv 0\pmod p\)。

1.2.2 算法流程

加入我们当前要判断的数是 \(p\)，我们考虑将 \(p-1\) 分解为 \(2^{k}\times t\) 的形式（显然一定可以分解出来）。当 \(p\) 是质数时，一定有 \(a^{2^{k}\times t}\equiv 1\pmod p\)。

那么我们就算出 \(a^t\) 的值，然后不断自乘去累加前面的 \(2^k\) 这一部分的指数。在自乘过程中利用二次探测定理进行判断，如果这一次自乘的数 \(\bmod p=1\)，但是上一次的数 \(\bmod p\ne \pm 1\)，那么这个数就是合数。同时最后自乘完还要利用费马小定理再判断一次。

那么现在的问题就只在于 \(a\) 的选择，事实上 \(a\) 可以取随机数，也可以取一些较小的质数，但是测试的轮数需要足够，一般取到 \(10\) 左右。

代码如下：

int prim[15] = {0, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41};

bool Miller_Rabin(int x) {
	if(x == 2) return 1;
	int t = x - 1, k = 0;
	while(!(t & 1)) t >>= 1, k++;
	for(int i = 1; i <= 13; i++) {
		if(x == prim[i]) return 1;
		int a = qpow(prim[i] % x, t, x), nxt;
		for(int j = 1; j <= k; j++) {
			nxt = a * a % x;
			if(nxt == 1 && a != 1 && a != x - 1) return 0;
			a = nxt;
		}
		if(a != 1) return 0;
	}
	return 1;
}

2 Pollard-Rho 算法

2.1 引入

首先考虑这样一个问题：给定一个正整数 \(N\)，找出它的一个非平凡因子（除 \(1\) 和 \(N\) 以外的因子）。

我们在基础数论中提到过可以利用试除法来求解，只需要枚举所有 \([1,\sqrt N]\) 中的数即可，复杂度是 \(O(\sqrt N)\) 的。但是如果 \(N\ge 10^{18}\)，这个复杂度无疑是十分差劲的，那么有没有更快的算法呢？

这个时候考虑我们的玄学方法，也就是随机化。我们在 \([1,\sqrt N]\) 里面随便猜一个数，显然其效率是 \(O(1)\) 的，不过正确率就降到了 \(10^{-18}\)​。那么有没有方式提高猜测的正确率呢？

事实上有，而这就是 Pollard-Rho 的基本思想。

2.2 生日悖论

首先我们需要引入一个东西叫做生日悖论。

我们考虑这样一个问题：假如一个房间中有 \(k\) 个人，那么当 \(k\) 达到多少时，其中两个人生日相同（不考虑闰年）的概率可以达到 \(50\%\)？

我们考虑正难则反，显然 \(k\) 个人生日互不相同的概率是 \(P=\dfrac{365}{365}\times\dfrac{364}{365}\times\dfrac{363}{365}\times\cdots\times\dfrac{365-k+1}{365}\)。也就是说生日有重复的概率 \(P'=1-\prod\limits_{i=1}^{k}\dfrac{365-i+1}{365}\)。实际上，当我们令 \(P'\ge \dfrac 12\) 时，可以解得 \(k\) 大概只要取到 \(23\) 以上即可。而当 \(k\) 取到 \(60\) 时，这个概率将会上升至 \(P'\approx 0.9999\)。实际上，假如一年中有 \(n\) 天，只需要 \(\sqrt{n}\) 级别的人数就可以满足要求。

上述数学模型与我们的实际经验严重不符，因此被称作生日悖论。

这个东西给了我们什么启发？考虑生日悖论的实质，实际上就是利用了 “组合随机采样” 的方法，满足答案的组合比单个个体要多，以此来提高正确率。那么怎么将这种思想运用到上面的分解因数中呢？

2.3 算法实现

2.3.1 随机算法的优化

我们利用 “组合随机采样” 的思想，考虑怎样进行组合。显然 \(n\) 与某个数的最大公约数一定是 \(n\) 的因数，也就是 \(\gcd(k,n)\mid n\)。那么我们只要选出一些 \(k\)，使得 \(1<\gcd(k,n)<n\)，那么就可以求出一个 \(n\) 的非平凡因子了。满足条件的 \(k\) 不少，\(n\) 的任意一个质因子的倍数都是可行的。

那么 Pollard-Rho 算法使用了一个随机函数生成一个序列 \(\{x_i\}\)。我们设 \(f(x)=(x^2+c)\bmod n\)，其中 \(c\) 是随机的一个常数。接下来随机选取一个 \(x_1\)，然后令 \(x_i=f(x_{i-1})\)。

如果你注意力较高，会发现一件事：由于 \(f\) 函数的取值只有 \(n\) 种，所以总会有一个时刻 \(x\) 数列的生成进入循环，得到相同的结果，如下图所示：

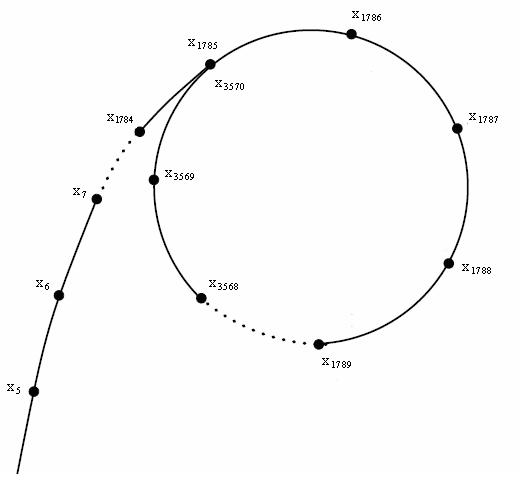
（发现它长得很像一个字母 \(\rho\)​，所以这个算法的名字叫做 Pollard-Rho）

根据生日悖论可知，这个数列中不同值的数量约为 \(O(\sqrt n)\) 个。这个时候我们设 \(m\) 是 \(n\) 的最小质因子，再生成一个数列 \(\{y_i\}\) 满足 \(y_i=x_i\bmod m\)。此时再根据生日悖论可知不同元素的个数约为 \(O(\sqrt m)\le O(n^{\frac 14})\)。于是我们可以在期望 \(O(n^{\frac 14})\) 的时间复杂度之内找出两个值 \(x_i,x_j\)，使得 \(x_i \ne x_j\) 且 \(y_i=y_j\)，这就说明 \(n \nmid |x_i-x_j|\) 且 \(m\mid |y_i-y_j|\)，即 \(\gcd(n,|x_i-x_j|)>1\)。

下面介绍 Pollard-Rho 算法的两种实现方式。

2.3.2 具体流程

2.3.2.1 Floyd 判环

考虑经典的小学奥数：两个人在同一个圆上跑，一快一慢，经过一段时间后两者必会相遇。那我们在 \(x\) 数列上模拟这个过程。设两个指针 \(a,b\)，一个以一倍速跑，一个以两倍速跑（即一个是 \(a\leftarrow f(a)\)，一个是 \(b\leftarrow f(f(b))\)），这样两者总会相遇，相遇时就出现了环。

然后我们每一次去记录两个 \(a,b\) 对应的 \(\gcd(|a-b|,n)\)，看是否符合条件。当出现环的时候，后面就不必再遍历了，此时如果没有找到因子就只能重新调整上述随机函数的参数然后重新分解。

代码如下：

int f(int x, int c, int n) {
	return (mul(x, x, n) + c) % n;
}

int Pollard_Rho(int n, int c) {
	int a, b;
	int x = rnd() % (n - 1) + 1;
	a = f(x, c, n), b = f(f(x, c, n), c, n);
	while(a != b) {
		int d = __gcd(abs(a - b), n);
		if(d > 1 && d < n) return d;
		a = f(a, c, n);
		b = f(f(b, c, n), c, n);
	}
	return n;
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0), cout.tie(0);
    //...
	int p = n;
	while(p >= n) {
		p = Pollard_Rho(n, rnd() % (n - 1) + 1);
	}
    //...
	return 0;
}

（实测证明，上述 Floyd 判环代码正确率较下面做法要低）

2.3.2.2 倍增优化

上述过程我们是在同时跑 \(a,b\)。在倍增优化中，我们每一次固定住 \(b\)，让 \(a\) 去跑一个固定的长度 \(k\)。每一次求出 \(\gcd(|a-b|,n)\) 并判断。当 \(a\) 跑完之后将 \(b\) 改为 \(a\)，同时 \(k\leftarrow 2\times k\)，然后不断重复上述过程直到 \(a,b\) 相遇。

代码如下：

int f(int x, int c, int n) {
	return (mul(x, x, n) + c) % n;
}

int Pollard_Rho(int n, int c) {
	int a, b, i = 1, k = 2;
	a = rnd() % (n - 1) + 1, b = a;
	while(1) {
		a = f(a, c, n);
		int d = __gcd(abs(a - b), n);
		if(d > 1 && d < n) return d;
		if(a == b) return n;
		if(++i == k) {
			k <<= 1;
			b = a;
		}
	}
	return n;
}