CF1503E 2-Coloring
cjx 组合强。
思路
观察一下题目,不难发现只有当黄色形成如下的单峰时才合法。
(染错色了,将就一下)
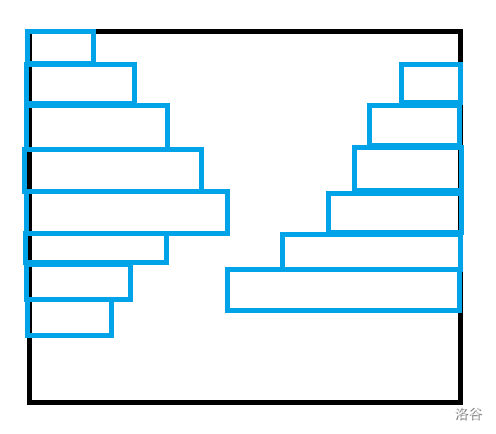
其中两座峰的峰顶高度相加等于 \(m\),为了方便统计,我们钦定右边的峰一定在左峰下方的行出现,最后答案乘以二就是最终方案。
发现对于每一边是两个最长不下降子序列拼在一起。
设 \(f[i][j]\) 为长度为 \(i\) 的最长不下降子序列,最高点高度为 \(j\) 的方案数。
再设 \(f'[i][j]\) 为长度为 \(i\) 的最长不下降子序列,仅有一个最高点为 \(j\) 的方案数。
答案就是
\[2\times \sum_{i=1}^n\sum_{j=i+1}^{n}\sum_{k=1}^{m-1} (f[i][k]\times f'[n-i+1][k])\times (f'[j][m-k]\times f[n-j+1][m-k]) \]相当于枚举第一个峰在行 \(i\),第二个峰在行 \(j\),第一个峰高度为 \(k\)。
变幻一下:
\[2\times \sum_{i=1}^n\sum_{k=1}^{m-1}(f[i][k]\times f'[n-i+1][k])\times \sum_{j=i+1}^{n} (f'[j][m-k]\times f[n-j+1][m-k]) \]这样给后一个和式做一个后缀和优化,即可把复杂度优化到 \(O(n^2)\) 级别。
当然有例外是这个样子。
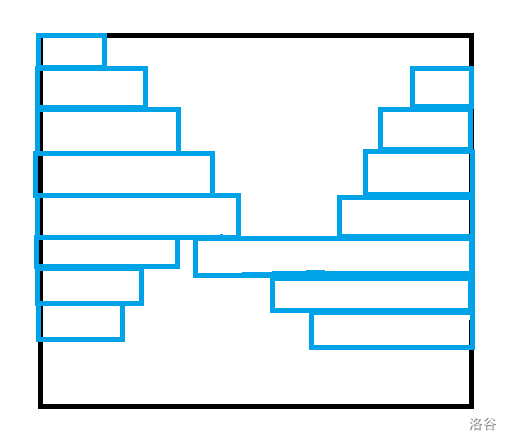
两峰交在一起(必须保证在连续的行且峰顶高度相加大于 \(m\)),也是一种方案。
\[2\times \sum_{i=1}^n\sum_{x=1}^{m-1}\sum_{y=1}^{m-1} (f[i][x]\times \sum_{k=1}^{y-1} f[n-i][k])\times (f[n-i][y]\times\sum_{k=1}^{x-1}f[i][k]) \]相当于枚举左边的峰顶在行 \(i\),左峰高度为 \(x\),右峰高度为 \(y\),同时求和了峰过后的一段不下降子序列的方案。
\[2\times \sum_{i=1}^n\sum_{x=1}^{m-1} (f[i][x]\times\sum_{k=1}^{x-1}f[i][k] )\sum_{y=1}^{m-1} (f[n-i][y]\times\sum_{k=1}^{y-1} f[n-i][k]) \]对于 \(\sum_{k=1}^{x-1}f[i][k]\) 和 \(\sum_{k=1}^{y-1} f[n-i][k]\) 前缀和优化。
然后预处理出所有的
\[f[n-i][y]\times\sum_{k=1}^{y-1} f[n-i][k] \]再次前缀和。
即可在 \(O(n^2)\) 的时间内求出上述和式。
对于 \(f\) 和 \(f'\) 的转移是容易的。
\[f[i][j]=\sum_{k=1}^j f[i-1][k] \]\[f'[i][j]=\sum_{k=1}^{j-1} f[i-1][k] \]初始值 \(f[0][0]=1\)。
其实你看到这里,已经可以使用 dp 做出本题了,但是如果你想进一步了解组合,请移步。
不难发现,我们每次的转移都相当于求一次前缀和,而 \(f[0][0]=1\)。
所以有可以构造这样的生成函数:
\[f[0]=1 \]观察 \(\sum_{i=0} x^i\) 的优雅性质,你会发现 \(1\times \sum_{i=0} x^i\) 相当于求一次前缀和。
而 \((\sum_{i=0} x^i)^2\) 相当于求两次前缀和(\(x^i\) 的系数是第 \(i\) 项的求前缀和后的值)。
由 \(f[0]\) 转移到 \(f[1]\) 的过程相当于乘以 \(\sum_{i=0} x^i\)(一次前缀和),所以有:
\[f[1][j]=[x^j](\sum_{k=0} x^k)^1 \]推广一下,每次 \(f[i]\) 向 \(f[i+1]\) 的转移都是乘以 \(\sum_{i=0} x^i\)(每转移一次求一次前缀和),所以有:
\[f[i][j]=[x^j](\sum_{k=0}x^k)^i \]对于 \(\sum_{i=0} x^i\),的封闭形式为 \((1-x)^{-1}\) 有很多种方法求,这里不再赘述。
所以有:
\[f[i][j]=[x^j](1-x)^{-i} \]使用广义二项式展开 \((1+(-x))^{-i}\),即可得到第 \(j\) 项的系数为:
\[\binom{-i}{j}=(-1)^j\binom{i+j-1}{j} \]关于牛顿二项式系数,已经有完备的公式,本处直接套公式即可,故不再展开讨论。
把系数乘上 \((-x)^j\),有
\[f[i][j]=\binom{i+j-1}{j} \]从比较简单的组合意义考虑,有 \(j\) 个球,有 \(i-1\) 个挡板,可以为空,两个挡板之间的球数相当于相邻两项的差。
那么有:
\[f[i][j]=\binom{i+j-1}{i-1}=\binom{i+j-1}{j} \]在观察一下 \(f'\) 求值的式子,你会发现 \(f'[i][j]=f[i][j-1]\)。
所以其实你也求出 \(f'\) 的组合意义了。
相当于有 \(j\) 个球,\(i-1\) 个挡板,最后一个挡板至少挡一个球,那么就可以投入 \(j-1\) 个球供所有挡板挡。
\[f'[i][j]=\binom{i+j-2}{j-1} \]如果考虑生成函数的话,\(f'[i][j]\) 相当于较 \(f[i][j]\) 向后平移了一个位置,那么可以写成:
\[f'[i][j]=[x^{j-1}](1-x)^{-i} \]或
\[f'[i][j]=[x^j](1-x)^{-i}x \]于是你就可以 愉快 的 AC 本题了。
CODE
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define N 5000
#define mod 998244353
const int maxn=5e3+5;
ll n,m,ans;
ll fac[maxn],inv[maxn],f[maxn];
inline ll ksm(ll x,ll y)
{
ll sum=1;
for(;y;y/=2,x=x*x%mod) if(y&1) sum=sum*x%mod;
return sum;
}
inline ll C(int n,int m)
{
if(n<m||m<0) return 0;
return 1ll*fac[n]*inv[m]%mod*inv[n-m]%mod;
}
int main()
{
freopen("magic.in","r",stdin);
freopen("magic.out","w",stdout);
for(int i=fac[0]=1;i<=N;i++) fac[i]=fac[i-1]*i%mod;
inv[N]=ksm(fac[N],mod-2);
for(int i=N-1;~i;i--) inv[i]=inv[i+1]*(i+1)%mod;
scanf("%lld%lld",&n,&m);
for(int h=1;h<n;h++)
{
for(int j=m;j>=2;j--)
{
f[j]=(1LL*f[j+1]+1LL*C(j+n-h-2,n-h-1)*C(m-j+n-h,n-h)%mod)%mod;
}
for(int i=m-1;i>=1;i--)
{
ans = (1LL*ans+1LL*C(i+h-1,h)*C(m-i+1+h-2,h-1)%mod*f[i+1]%mod)%mod;
}
}
memset(f,0,sizeof(f));
for(int x=1;x<=m;x++)
{
for(int j=n-1;j>=1;j--)
{
f[j]=(1LL*f[j+1]+1LL*C(m-x+n-j-1,n-j-1)*C(m-x+j-1,j)%mod)%mod;
}
for(int i=1;i<n;i++)
{
ans=(1LL*ans+1LL*C(x+i-1,i)*C(x+n-i-1,n-i-1)%mod*f[n-i+1]%mod)%mod;
}
}
printf("%lld\n",ans*2%mod);
}