等差幂线
\(AB\perp CD\iff AC^2-AD^2=BC^2-BD^2\)
圆幂
定义一个点关于 \(\odot O\) 的圆幂 \(\rho_o(A)=OA^2-R^2\) :
若 \(A\) 在圆外, \(APQ\) 是 \(\odot O\) 的割线,则 \(AP\cdot AQ=\rho_o(A)\)
若 \(A\) 在圆内, \(PAQ\) 是 \(\odot O\) 的弦,则 \(AP\cdot AQ=-\rho_o(A)\)
特别地,对于点圆的幂即 \(\rho_O(A)=OA^2\)
根轴
两圆的根轴定义为满足 \(\rho_{O_1}(A)=\rho_{O_2}(A)\) 的点 \(A\) 的集合,连心线垂直于根轴
特别地,当两圆相交,两圆交点连线在根轴上,并被连心线垂直平分

根心定理:三圆两两根轴要么平行,要么交于一点。(直接利用根轴的定义,等式的传递性)
逆定理:如图,若 \(MN\cap ST\) 在 \(\odot O_1,\odot O_2\) 的根轴上,那么这四点共圆。
例1
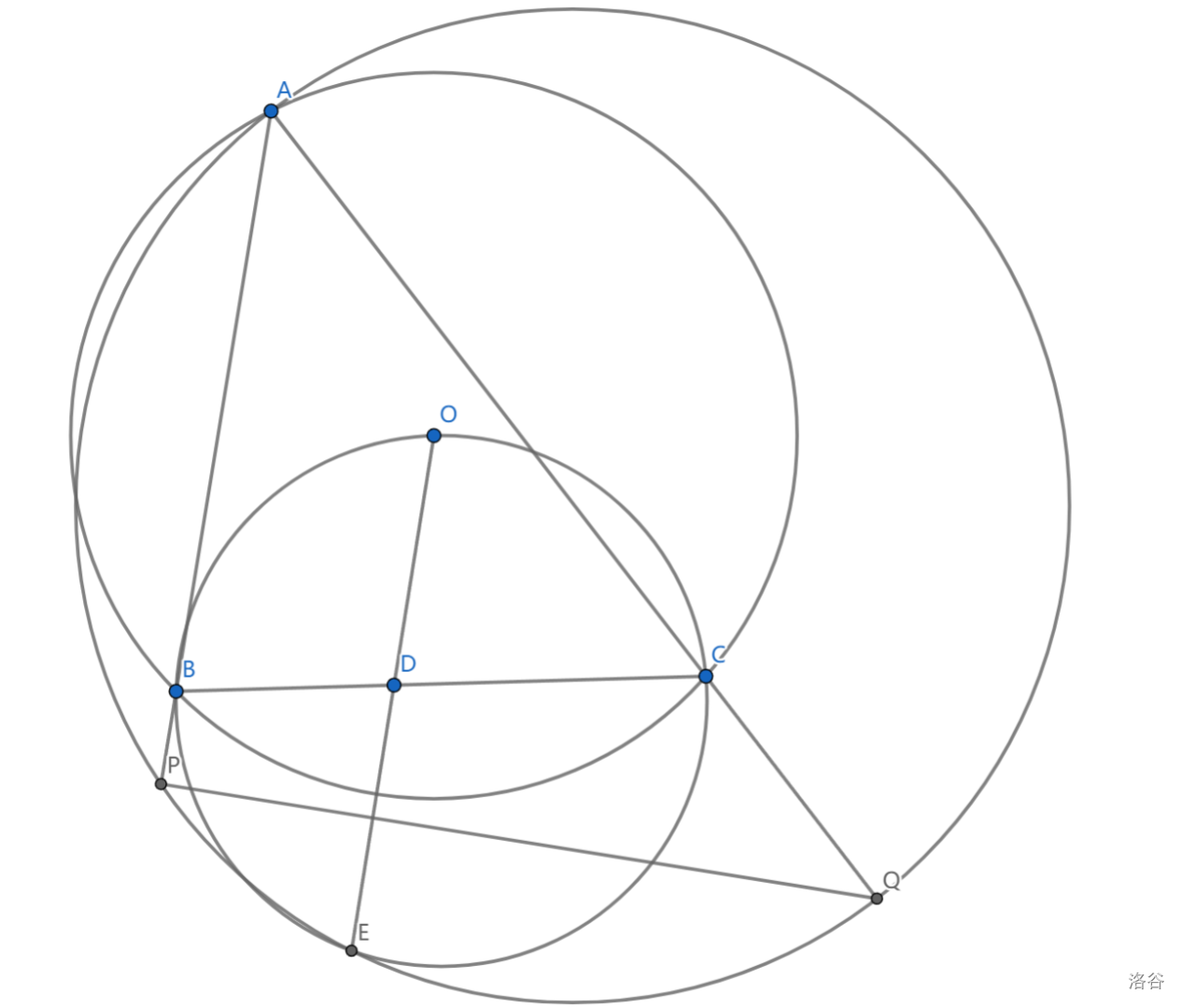
如图, \(\triangle ABC\) 内接于 \(\odot O\) , \(D\) 是 \(BC\) 上任一点, \(ODE\) 是 \(\odot (OBC)\) 一条弦,\(P,Q\) 是 \(DE\) 中垂线与 \(AB,AC\) 的交点,求证: \(APEQ\) 共圆
这里我们以圆幂,割线的视角来看这个问题
\(\rho_O(P)=PB\cdot PA=OP^2-OB^2\)
由于 \(PD=PE\) ,将 \(D,E\) 视作 \(\odot P\) 上的点,有 \(\rho_P(O)=OD\cdot OE=OP^2-PD^2\)
这里我们要注意一个弧中点( \(O\) 为 \(BC\) 中点)的常用结论:\(OD\cdot OE=OB^2\)
综上可以得到 \(PD^2=PB\cdot PA\) ,即 \(\triangle PDB\sim \triangle PAD\)
同理 \(\triangle QDC\sim\triangle QAD\)
\(\angle PDB+\angle QDC=\angle PAD+\angle QAD=\angle A\) ,从而 \(\pi-\angle A=\angle PED\) ,即证
例2
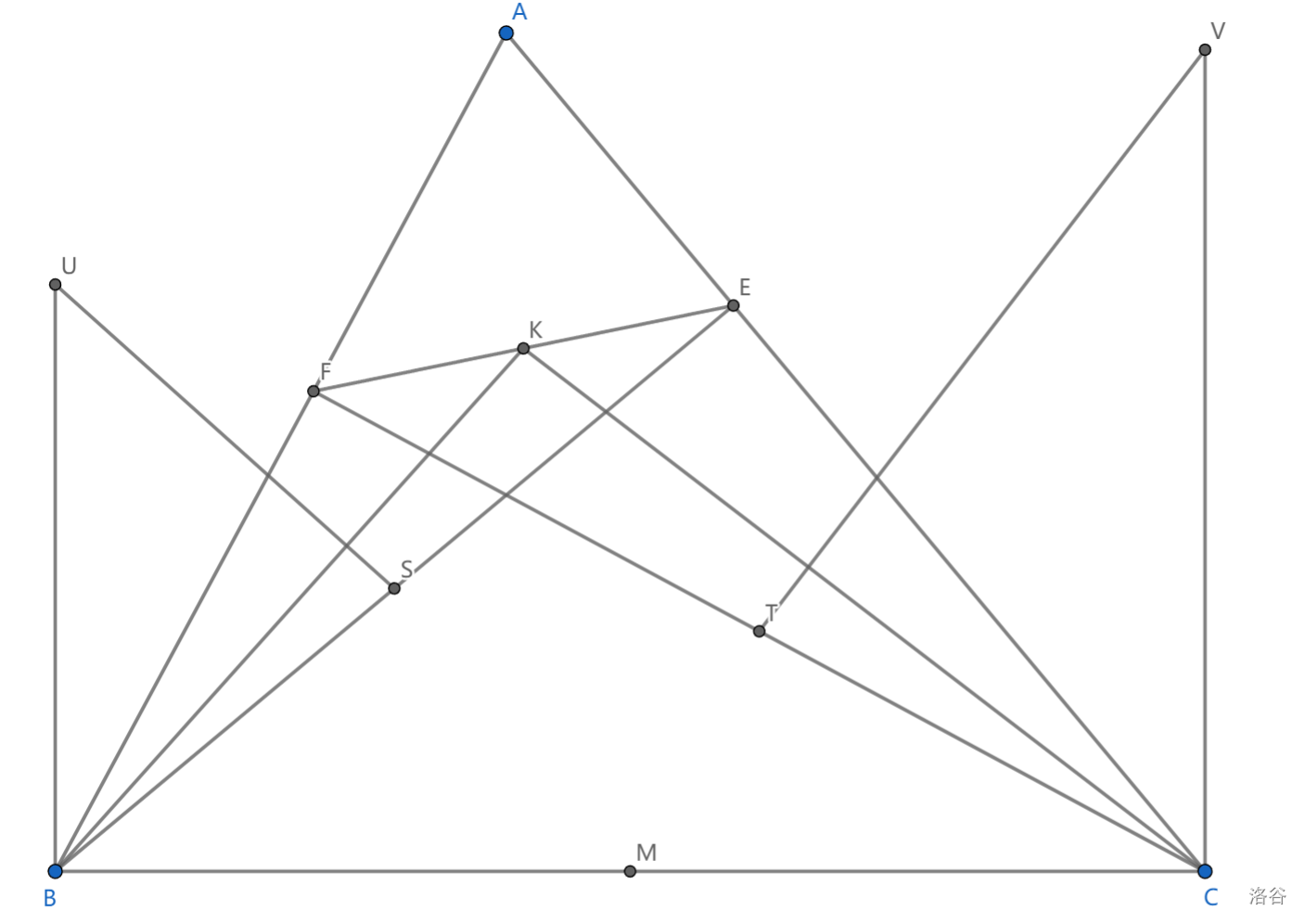
如图,锐角 \(\triangle ABC\) 中, \(BE,CF\) 是两条高, \(K,S,T\) 分别是 \(EF,BE,CF\) 的中点,过 \(S\) 作 \(BK\) 的垂线与过 \(B\) 垂直 \(BC\) 的直线交于点 \(U\) ,过 \(T\) 作 \(CK\) 的垂线与过 \(C\) 垂直于 \(BC\) 的垂线交于点 \(V\) ,求证: \(UV//EF\)
我们取 \(BC\) 中点 \(M\) ,则 \(MK\perp EF\) ,下证明 \(KM\perp UV\)
根据 \(US\perp BK\) ,有 \(BU^2-KU^2=BS^2-KS^2=\frac14 (BE^2-BF^2)\)
根据勾股定理,有 \(UM^2=\frac14BC^2+BU^2\)
两式结合可知 \(UM^2-UK^2=\frac14(BC^2+BE^2-BF^2)\)
同理 \(VM^2-VK^2=\frac14(BC^2+CF^2-CE^2)\)
显然 \(BE^2+CE^2=BF^2+CF^2\) ,即证
例3
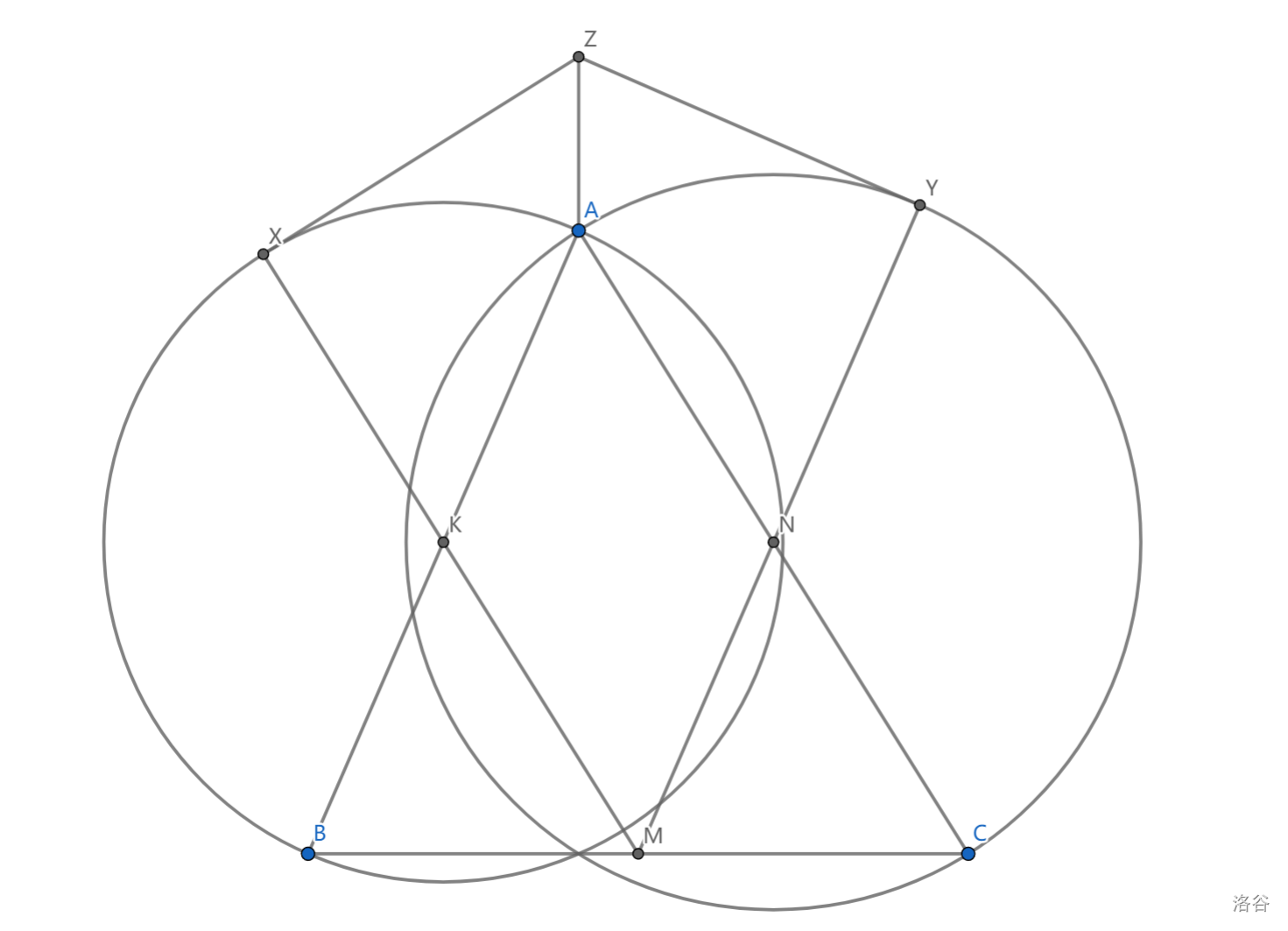
如图, \(\triangle ABC\) 三边中点分别为 \(M,N,K\) ,以 \(AB,AC\) 为直径的圆分别与 \(MK,MN\) 交于点 \(X,Y\) ,过 \(X,Y\) 分别作两圆切线交于 \(Z\) ,求证 \(AZ\perp BC\)
只需注意到两圆另一交点即 \(A\) 在 \(BC\) 上投影,只需证 \(Z\) 在根轴上
即证 \(ZX=ZY\) ,即证 \(MX=MY\) ,实际上 \(MX=MK+XK=\frac12 AC+\frac12 AB=NY+NM=MY\)
例4
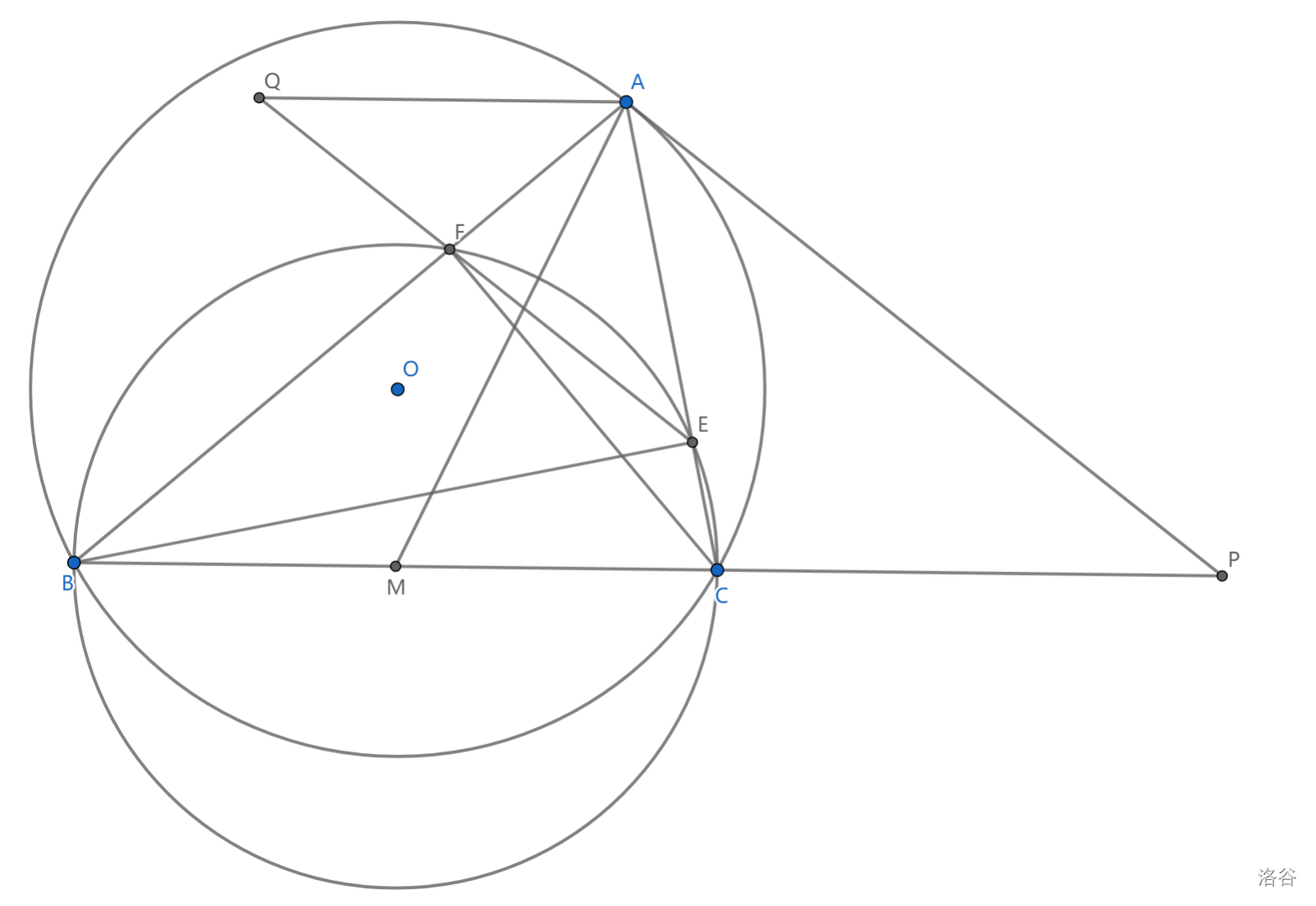
如图,锐角三角形 \(ABC\) 满足 \(AB>AC\) , \(BE,CF\) 是两条高,\(EF\) 与过 \(A\) 且平行于 \(BC\) 的直线交于 \(Q\) ,过 \(A\) 作 \(\triangle ABC\) 外接圆切线与 \(BC\) 延长线交于点 \(P\) ,\(M\) 为 \(BC\) 中点,求证 \(AM\perp PQ\)
这里注意到 \(PA^2=PC\cdot PB\) ,也就是说 \(P\) 到点圆 \(A\) 和 \(\odot (BCEF)\) 的圆幂是相等的,我们希望证明 \(Q\) 到两圆的圆幂也相等
\(\iff QA^2=QF\cdot QE\)
实际上由 \(AQ//BC\) 可知 \(\angle QAF=\angle ABC=\angle AEQ\) ,从而 \(\triangle AQF\sim \triangle EAQ\) ,即证
例5
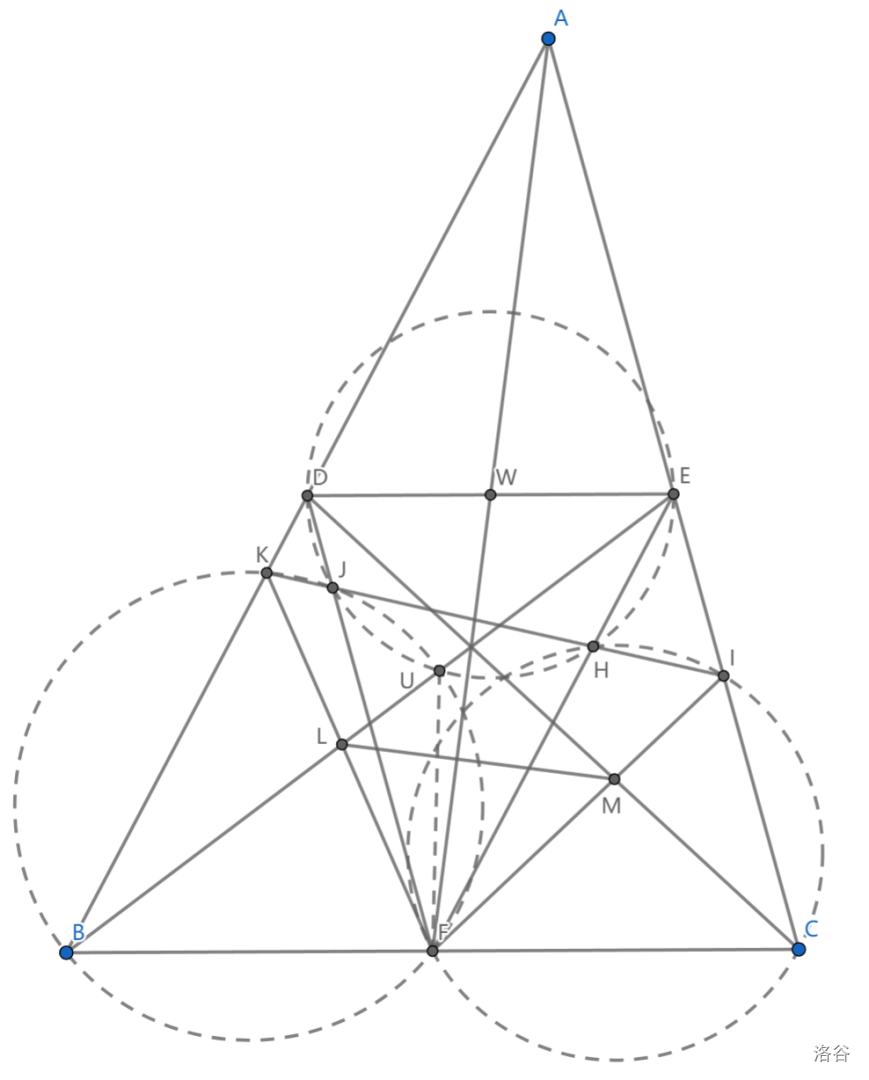
如图, \(\triangle DEF\) 是中点三角形, \(J,H\) 是 \(DF,EF\) 上的垂足, \(JH\) 与 \(AB,AC\) 交于 \(K,I\) , \(BE\cap KF=L,CD\cap FI=M\) ,求证: \(AF\perp LM\)
首先,由 \(\angle KJF=\angle DJH,\angle KBF=\angle DEF\) ,可知 \(\angle KJF+\angle KBF=\pi\) , \(KJFB\) 共圆
由 \(DE//BF,DF\) 过两圆交点 \(J\) ,可知两圆另一交点在 \(BE\) 上( \(Reim\) 引理 )
又 \(\angle LUF=\angle BUF=\angle BKF=\angle EFK=\angle EFL\) ,知 \(\triangle LUF\sim\triangle LEF\) ,即 \(LU\cdot LE=LF^2\) , \(L\) 关于点圆 \(F\) 及 \(\odot(DJHF)\) 的幂相等, 同理 \(M\) 相等,即证
下面我们将展示一些进阶的构型。

如图,若 \(l\) 是 \(\odot O_1,\odot O_2\) 的根轴, \(P\) 到 \(l\) 的投影是 \(H\) ,则有
\(\rho_{\odot O_1}(p)-\rho{\odot O_2}(p)=2\overline{PH}\cdot O_1O_2\)
这个引理非常容易计算证明,它给出了下面两个命题:
-
三圆 \(\odot O_1,\odot O_2,\odot O_3\) 共轴的充要条件是 \(\odot O_3\) 上两点 \(P,Q\) 满足 \(\rho_{\odot O_1}(P)/rho_{\odot O_2}(P)=\rho_{\odot O_1}(Q)/rho_{\odot O_2}(Q)\)
-
三点共线的充要条件是它们关于两圆幂的差是线性关系。
进一步地我们将介绍 \(Poncelet\) 共轴引理(它实际上是 \(Poncelet\) 闭合定理中用到的引理):

\(AB,XY\) 是圆 \(c_1\) 上的两条弦,与圆 \(c_2\) 切于点 \(M,N\) ,延长 \(MN\) 交 \(BX,AY\) 于 \(S,T\) ,则过 \(S,T\) 与 \(BX,AY\) 相切的圆与 \(c_1,c_2\) 共轴。
这是很容易证明的,只要说明 \(\frac{AT}{AM}=\frac{BS}{BM}\) ,用正弦定理,我们看到只要 \(\angle XST=\angle AST\) ,它们是相等的弦切角。

这里还有一个常见的构型,是基于第一个命题的,考虑图中的两个圆和它们的切点 \(X\) (点圆)是共轴的,从 \(BC\) 出发作计算,我们将看到
\(\frac{BX}{CX}=\sqrt\frac{BS\cdot BT}{CS\cdot CT}\)
这意味着,给定点 \(S,T,X\) ,这样的小圆是唯一确定的。
例1

如图,四边形 \(ABCD\) 内接于 \(\odot O\) , \(I,J\) 为 \(\triangle ABC,ABD\) 的内心,直线 \(IJ\) 分别交 \(AD,AC,BD,BC\) 于 \(P,M,N,Q\) ,过 \(M,N\) 作 \(AC,BD\) 的垂线交于 \(X\) ,过 \(P,Q\) 作 \(AD,BC\) 的垂线交于 \(Y\) ,求证: \(XYO\) 共线
这道题是 \(Poncelet\) 共轴引理的一个直接引用。我们先要给出 \(IJ\) 线的一些性质

如图,根据鸡爪定理,我们看到 \(SI=SC=SJ,TI=TB=TJ\) ,从而 \(ST\perp IJ\) ,而 \(\angle AKB\) 的平分线平行于 \(ST\) ,从而 \(\angle AKB\) 的平分线垂直 \(MN\) ,所以 \(KM=KN\) ,进而 \(XM=XN\)
并且 \(\angle DAC=\angle DBC\) ,则外角 \(\angle DPQ=\angle CQP\) ,进而 \(YP=YQ\) ,作两个圆,然后用 \(Poncelet\) 共轴引理。
例2
\(\triangle A_1B_1C_1,\triangle A_2B_2C_2\) 拥有相同的垂心与外接圆,垂心为 \(H\) ,外心为 \(O\) ,直线 \(A_1A_2,B_1B_2,C_1C_2\) 围成 \(\triangle PQR\) ,证明: \(\triangle PQR\) 的外心在直线 \(OH\) 上
这两个圆拥有相同的九点圆圆心,我们关于 \(O\) 反演,\(A_1C_1\) 中点变为了 \(A_1C_1\) 关于 \(\odot O\) 的极点(并不是看到九点圆就应当关于 \(H\) 反演的,至少这道题不行)

我们设出这些对应的极点构成了 \(\triangle X_1Y_1Z_1,\triangle X_2Y_2Z_2\) ,它们的内切圆与外接圆相同,我们要证的是三圆共轴(因为反演后九点圆圆心依旧在线 \(OH\) 上,尽管它不是大圆的圆心)
我们知道 \(X_1PX_2\) 共线(射影几何(1) 引理 \(9.3\) ),然后设出 \(X_1X_2,Y_1Y_2,Z_1Z_2\) 交出的三角形 \(UVW\) ,希望借助这个三角形完成我们的工作。
我们注意到 \(\angle URQ=\angle A_1RZ_1=\angle Y_1A_1A_2-\angle YZ_1Z_2=\angle Z_2A_2A_1-\angle Z_2Y_2Y_1=\angle UQR\) (用一些简单的弦切角),所以 \(UR=UQ\) ,其它也是同理
这实际上说明了 \(\triangle PQR\) 的外接圆内切于 \(\triangle UVW\)
现在我们准备好计算圆幂比值,我们看
\(\large (\frac{X_1B_1}{X_1P_1})^2=(\frac{\sin \angle X_1PB_1}{\sin \angle X_1B_1P})^2=(\frac{\sin Z_2RB_2}{\sin Z_2B_2R})^2=(\frac{Z_2B_2}{Z_2R})^2\)
这就完成了证明。
例3

如图, \(I\) 为 \(\triangle ABC\) 的内心,圆 \(c_1\) 与 \(AB,AC\) 切于点 \(P,Q\) ,圆 \(c_2\) 过点 \(B,C\) 并与 \(c_1\) 切于点 \(M\) ,证明: \(PBMI,QCMI\) 分别共圆
我们假设 \(\odot (CQI)\cap \odot(BPI)=M'\) ,我们看到 \(\angle PM'Q=\angle PM'I+\angle QM'I=\angle PBI+\angle QCI=\frac B2+\frac C2=\angle APQ\) ,所以 \(M'\in c_1\)
圆 \(c_2\) 并没什么用处,我们用上面提到的构型尝试消去,我们要证的是
\(\frac{BM'}{CM'}=\frac{BP}{CQ}\) (右边就是 \(B,C\) 到这个圆的幂)
我们设出了 \(M'\) 是两圆交点,对这个性质还没有利用完全。我们得找一些旋转相似(这里 \(Reim\) 不是很现实)已经知道了 \(M'\in c_1\) ,所以可以看到 \(\triangle BP'M\sin \triangle ISM'\)
类似构造点 \(T\) ,因为 \(P,Q\) 关于 \(AI\) 对称,所以 \(S,T\) 也会关于 \(AI\) 对称,从而 \(IS=IT\)
而两组相似给出了 \(\frac{BP}{BM'}=\frac{IS}{IM'},\frac{CP}{CM'}=\frac{IT}{IM'}\) ,这就证毕。
例4
