前言
题目链接:Hydro & bzoj。
题意简述
一棵 \(n\) 个结点的树上,每个点有点权,有 \(m\) 次操作:
- 修改 \(u\) 的点权;
- 查询以 \(u\) 为一端的简单路径的点权和最大值。
- 对于 \(20 \%\) 的数据:\(n, m \leq 10^3\);
- 对于另 \(30 \%\) 的数据:第 \(i\) 条边连接 \(i\) 和 \(i + 1\);
- 对于另 \(20 \%\) 的数据:除了 \(1\) 号点,\(i\) 和 \(\Big \lfloor \cfrac{i}{2} \Big \rfloor\) 连边;
- 对于另 \(10 \%\) 的数据:树的深度不超过 \(40\);
- 对于 \(100 \%\) 的数据:\(n, m \leq 10^5\)。
这是 NFLS 上的范围,原 bzoj 的数据太水了(没有最后一档满分),Hydro 上还有奇怪的压缩读入。
题目分析
\(20 \%\) 部分分
修改直接 \(\Theta(1)\) 改,查询的时候以 \(u\) 为起点搜一遍,记录最值即可。
时间复杂度 \(\Theta(nm)\)。
\(50 \%\) 部分分
是一条链的情况。
不妨假设终点 \(v\) 在 \(u\) 的左侧,另一侧同理。我们看看从 \(u\) 走到 \(v\) 的价值和为 \(\sum \limits _ {i = v} ^ u val_i\),不妨做个前缀和,即为 \(sum_u - sum_{v-1}\),对于 \(u\),\(sum_u\) 是不变的,而我们希望答案最大,所以希望找到 \(sum_{v-1}\) 的最小值。右侧同理,但是最大值。修改的时候,要把右侧的前缀和统统加上增量。想到线段树维护区间加、区间查询最值。
时间复杂度 \(\Theta(m \log n)\)。
\(70 \%\) 部分分
完全二叉树,深度很小,是 \(\Theta(\log n)\) 的,考虑从这里优化。
发现答案可以有以下部分构成:
- \(u\) 出发向子树里走;
- \(u\) 先向上走到 \(v\),再走到 \(v\) 的另一个儿子的子树里。
由于深度很小,后者暴力跳父亲是正确的。结合前者,我们希望快速求出,从一个点开始,走到子树里某一个点停下,这段路程的最大值。由于只会向下走,考虑上树上差分,即求 \(sum_v - sum_{\operatorname{fa}(u)}\) 的最大值。后者是定值,相当于在子树里找到 \(sum_v\) 的最大值。上一棵线段树就可以了,DFS 序加线段树维护即可。修改子树修改,查询同样子树查询。
时间复杂度:\(\Theta(m \log ^ 2 n)\)。
\(80 \%\) 部分分
与二叉树唯一不同的是,跳到一个节点 \(u\),他的兄弟可能不止一个。其实也很简单,用 \(\operatorname{fa}(u)\) 的 DFS 序表示的区间减去 \(u\) 的 DFS 序表示的区间即可。
时间复杂度:\(\Theta(m \log ^ 2 n)\)。
\(100 \%\) 部分分
好吧,其实就是满分。
如果树深度很深,有什么办法?把重心当根骗分?可以是可以,但是一分没骗到。想到点分树深度也是 \(\Theta(\log n)\) 级别的,以及树链剖分到根节点跳的次数是 \(\Theta(\log n)\) 的,产生了这题的两种解决方式。
点分树
从原树到点分树,虽然深度降低了,但是在某些程度上破坏了原树上点对之间的关系,会有哪些区别呢?
先来考虑询问,我们暴力跳点分树的父亲,我们希望求出当前分治中心除了跳上来的这个子树,其他子树里的每一个点到分治中心的最大值。类似地,想到可以每一个分治中心开一棵线段树,然后也跑一遍 dfs,记录 dfs 序,线段树查询最大值。
由于深度很小,我们记 \(L[u][d] \sim R[u][d]\) 表示 \(u\) 在点分树上深度为 \(d\) 时的 dfs 序区间,同时 \(rtdpt_u\) 表示 \(u\) 在点分树上的深度。
初始答案就是 \(val_u\) 和 \(u\) 这个分治中心的最大值之和。记上一次跳上来的分治中心是 \(lst\),当前所在分治中心为 \(v\)。我们处理的时候也要知道当前从 \(u\) 开始,已经得到的价值之和。注意到,由于点分树破坏了原树上点对之间的关系,所以不能直接把 \(lst\) 到 \(v\) 路径上的 \(\sum val\) 累加起来。这个解决方法也很简单,在 \(v\) 上直接查询 \(u\) 到它的价值之和即可,即查询 \(L[u][rtdpt_v] \sim L[u][rtdpt_v]\) 的最大值。
那么,我们在 \(v\) 整棵线段树上“扣掉”的区间就是 \(L[u][rtdpt_v] \sim R[u][rtdpt_v]\) 吗?并不是!时刻记住点分树会破坏原树结构。这里,可能会出现下图情况:
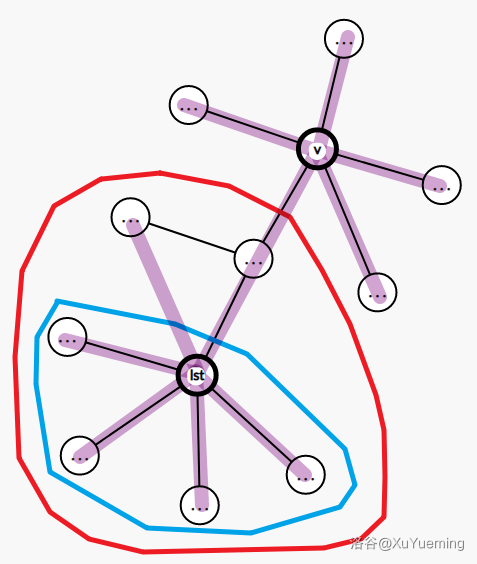
上图中,紫色的边是点分树的边。发现,如果直接用 dfs 序,扣掉了蓝色部分的区间,但是我们想要扣掉红色部分。解决方法不用想太复杂了,在点分治的时候,除了记录点分树上的父亲,再一个“关键点”,即从点分树父亲走向儿子在原树上的第一个结点。这样就没什么问题了。
接下来看看修改。由于我们线段树存的值不包括当前分治中心,所以 \(u\) 和它子树没什么要改的。考虑它点分树上一个祖先 \(v\),\(u\) 到 \(v\) 之间的值只有 \(u\) 发生了变化,那么我们不做赋值,把增量加上去就能完美解决。
时间复杂度:\(\Theta(n \log n + m \log ^ 2 n)\),空间复杂度:\(\Theta(n \log n)\)。
树链剖分
树链剖分想法类似。我们需要快速求出重链上的信息。考虑假设我们当前在 \(v\),其经过这条重链的答案总是可以被表示为 \(v \overset{\text{重链}}{\longrightarrow} x_1 \overset{\text{轻边}}{\longrightarrow} x_2 \ldots x_k\)。那么查询便是:\(x\) 到 \(v\) 的权值之和加上从 \(x\) 出发,往轻儿子里走的权值和最大值。那么我们线段树上结点需要维护 \((sum, lmx, rmx)\) 表示这段重链权值和,从顶出发和从底出发的答案。假设 \(p_x\) 表示从 \(x\) 出发往轻儿子走的最优答案,初值一个点的答案为 \((val_x, val_x + p_x, val_x + p_x)\)。合并操作很简单。
查询的时候,不断往上跳,并记录 \(sum\) 维护从 \(u\) 到当前 \(v\) 的价值和,同时统计答案。注意,如果当前在 \(v\),我们查询 \(\operatorname{top}(v) \sim \operatorname{fa}(v)\) 的 \(rmx\),即不能包含 \(v\),原因是我们不能把重新往来的这条边往下走的答案统计进去,另一边同理。那怎么计算走到 \(v\) 的另一个轻儿子的答案呢?只用记录一个次大值就行了。
至于修改,也是不断向上跳,尝试更新。如果当前整条重链的 \(lmx\) 发生变化,则需要更新 \(t = \operatorname{fa}(\operatorname{top}(v))\) 的信息,即在 \(p\) 中删除原先的 \(lmx + val_t\) 的贡献,再加入新的贡献。看到 \(p\) 要支持删除、查询最值和次最值,可以用 set 记录二元组 \((lmx + val_{\operatorname{fa}(\operatorname{top}(v))}, \operatorname{top}(v))\)。
时间复杂度:\(\Theta(n \log n + m \log ^ 2 n)\),空间复杂度:\(\Theta(n)\)。
代码
以下是全部详细部分分。
奇怪读入及基本框架
点击查看代码
/*
* Problem link: https://hydro.ac/d/bzoj/p/2158
* My Solution : https://www.cnblogs.com/XuYueming/p/18347278
**/
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <set>
using namespace std;
#define Hydro
#ifdef XuYueming
# define printf printf(">>>>>>>>> "), printf
#endif
const int N = 100010;
struct Question {
int op, u, x;
} qry[N];
struct Graph {
struct node {
int to, nxt;
} edge[N << 1];
int tot = 1, head[N];
void add(int u, int v) {
edge[++tot] = {v, head[u]};
head[u] = tot;
}
inline node & operator [] (const int x) {
return edge[x];
}
} xym;
int n, m, val[N], eu[N], ev[N];
void compressInput() {
int L, now, A, B, Q, tmp;
scanf("%d%d%d%d%d%d%d", &n, &m, &L, &now, &A, &B, &Q), --m;
for (int i = 1; i <= n; ++i) {
now = (now * A + B) % Q, tmp = now % 10000;
now = (now * A + B) % Q;
if (now * 2 < Q) tmp *= -1;
val[i] = tmp;
}
for (int i = 1; i < n; ++i) {
now = (now * A + B) % Q;
tmp = (i < L) ? i : L;
eu[i] = i - now % tmp, ev[i] = i + 1;
xym.add(eu[i], ev[i]), xym.add(ev[i], eu[i]);
}
for (int i = 1; i <= m; ++i) {
now = (now * A + B) % Q;
if (now * 3 < Q) {
now = (now * A + B) % Q;
qry[i].op = 1;
qry[i].u = now % n + 1;
} else {
qry[i].op = 2;
now = (now * A + B) % Q, tmp = now % 10000;
now = (now * A + B) % Q;
if (now * 2 < Q) tmp *= -1;
now = (now * A + B) % Q;
qry[i].u = now % n + 1, qry[i].x = tmp;
}
}
}
void commonInput() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &val[i]);
for (int i = 1; i <= n - 1; ++i) scanf("%d%d", &eu[i], &ev[i]), xym.add(eu[i], ev[i]), xym.add(ev[i], eu[i]);
while (true) {
static char op[10];
scanf("%s", op);
if (*op == 'D') break;
++m;
if (*op == 'Q') {
qry[m].op = 1, scanf("%d", &qry[m].u);
} else {
qry[m].op = 2, scanf("%d%d", &qry[m].u, &qry[m].x);
}
}
}
signed main() {
#ifdef Hydro
char _[2]; scanf("%s", _);
#ifdef XuYueming
commonInput();
#else
compressInput();
#endif
#else
#ifndef XuYueming
freopen("lycoris.in", "r", stdin);
freopen("lycoris.out", "w", stdout);
#endif
commonInput();
#endif
if (pts1::check()) return pts1::solve(), 0;
if (pts2::check()) return pts2::solve(), 0;
if (pts3::check()) return pts3::solve(), 0;
return n & 1 ? ACcode1::solve() : ACcode2::solve(), 0;
}
\(20 \%\) 部分分
点击查看代码
namespace pts1 {
inline bool check() {
return n <= 1000;
}
int mx;
void dfs(int now, int sum, int fa) {
mx = max(mx, sum);
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa) continue;
dfs(to, sum + val[to], now);
}
}
void solve() {
for (int i = 1; i <= m; ++i) {
if (qry[i].op == 2) {
val[qry[i].u] = qry[i].x;
} else {
mx = -0x3f3f3f3f, dfs(qry[i].u, val[qry[i].u], 0);
printf("%d\n", mx);
}
}
}
}
\(50 \%\) 部分分
点击查看代码
namespace pts2 {
inline bool check() {
for (int i = 1; i <= n - 1; ++i)
if (eu[i] != i || ev[i] != i + 1)
return false;
return true;
}
struct Segment_Tree {
#define lson (idx << 1 )
#define rson (idx << 1 | 1)
struct node {
int l, r;
int mx, mi;
int lazy;
} tree[N << 2];
void pushtag(int idx, int v) {
tree[idx].lazy += v;
tree[idx].mx += v;
tree[idx].mi += v;
}
void pushdown(int idx) {
if (tree[idx].lazy == 0) return;
pushtag(lson, tree[idx].lazy);
pushtag(rson, tree[idx].lazy);
tree[idx].lazy = 0;
}
inline void pushup(int idx) {
tree[idx].mx = max(tree[lson].mx, tree[rson].mx);
tree[idx].mi = min(tree[lson].mi, tree[rson].mi);
}
void build(int idx, int l, int r) {
tree[idx].l = l, tree[idx].r = r;
if (l == r) return pushtag(idx, val[l]);
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(idx);
}
void modify(int idx, int l, int r, int v) {
if (tree[idx].l > r || tree[idx].r < l) return;
if (l <= tree[idx].l && tree[idx].r <= r) return pushtag(idx, v);
pushdown(idx);
modify(lson, l, r, v);
modify(rson, l, r, v);
pushup(idx);
}
int querymi(int idx, int l, int r) {
if (tree[idx].l > r || tree[idx].r < l) return 0x3f3f3f3f;
if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].mi;
return pushdown(idx), min(querymi(lson, l, r), querymi(rson, l, r));
}
int querymx(int idx, int l, int r) {
if (tree[idx].l > r || tree[idx].r < l) return -0x3f3f3f3f;
if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].mx;
return pushdown(idx), max(querymx(lson, l, r), querymx(rson, l, r));
}
int query(int p) {
return querymi(1, p, p);
}
#undef lson
#undef rson
} yzh;
int tmp[N];
void solve() {
for (int i = 1; i <= n; ++i) tmp[i] = val[i], val[i] += val[i - 1];
yzh.build(1, 0, n);
for (int i = 1; i <= m; ++i) {
int u = qry[i].u, x = qry[i].x;
if (qry[i].op == 2) {
yzh.modify(1, u, n, x - tmp[u]);
tmp[u] = x;
} else {
int mx = -0x3f3f3f3f;
mx = max(mx, yzh.query(u) - yzh.querymi(1, 0, u - 1));
if (u + 1 <= n)
mx = max(mx, yzh.querymx(1, u + 1, n) - yzh.query(u - 1));
printf("%d\n", mx);
}
}
}
}
\(80 \%\) 部分分
\(70 \%\) 和 \(80 \%\) 的区别不大,只给出 \(80 \%\) 的代码。
点击查看代码
namespace pts3 {
int mxdpt;
void dfs(int now, int fa) {
static int dpt[N];
mxdpt = max(mxdpt, dpt[now]);
if (dpt[now] > 40) return;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa) continue;
dpt[to] = dpt[now] + 1, dfs(to, now);
if (mxdpt > 40) return;
}
}
inline bool check() {
return dfs(1, 0), mxdpt <= 40;
}
struct Segment_Tree {
#define lson (idx << 1 )
#define rson (idx << 1 | 1)
struct node {
int l, r;
int mx, lazy;
} tree[N << 2];
void pushtag(int idx, int v) {
tree[idx].lazy += v;
tree[idx].mx += v;
}
void pushdown(int idx) {
if (tree[idx].lazy == 0) return;
pushtag(lson, tree[idx].lazy);
pushtag(rson, tree[idx].lazy);
tree[idx].lazy = 0;
}
inline void pushup(int idx) {
tree[idx].mx = max(tree[lson].mx, tree[rson].mx);
}
void build(int idx, int l, int r) {
tree[idx].l = l, tree[idx].r = r;
if (l == r) return;
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(idx);
}
void modify(int idx, int l, int r, int v) {
if (tree[idx].l > r || tree[idx].r < l) return;
if (l <= tree[idx].l && tree[idx].r <= r) return pushtag(idx, v);
pushdown(idx);
modify(lson, l, r, v);
modify(rson, l, r, v);
pushup(idx);
}
int query(int idx, int l, int r) {
if (tree[idx].l > r || tree[idx].r < l) return -0x3f3f3f3f;
if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].mx;
return pushdown(idx), max(query(lson, l, r), query(rson, l, r));
}
int query(int p) {
return query(1, p, p);
}
#undef lson
#undef rson
} yzh;
int fa[N], L[N], R[N], timer;
void dfs(int now) {
L[now] = ++timer;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa[now]) continue;
fa[to] = now;
dfs(to);
}
R[now] = timer;
yzh.modify(1, L[now], R[now], val[now]);
}
int root, siz[N];
void findroot(int now, int fa) {
siz[now] = 1;
int mx = 0;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa) continue;
findroot(to, now);
siz[now] += siz[to];
mx = max(mx, siz[to]);
}
mx = max(mx, n - siz[now]);
if (mx <= n / 2) root = now;
}
void solve() {
yzh.build(1, 1, n), findroot(1, 0), dfs(root);
for (int i = 1; i <= m; ++i) {
int u = qry[i].u, x = qry[i].x;
if (qry[i].op == 2) {
yzh.modify(1, L[u], R[u], x - val[u]);
val[u] = x;
} else {
int su = yzh.query(L[u]);
int mx = val[u] + yzh.query(1, L[u], R[u]) - su;
for (int lst = u, v = fa[u]; v; lst = v, v = fa[v]) {
// L[v]~R[v] L[lst]~R[lst]
int res = -0x3f3f3f3f;
if (L[v] < L[lst]) res = max(res, yzh.query(1, L[v], L[lst] - 1));
if (R[v] > R[lst]) res = max(res, yzh.query(1, R[lst] + 1, R[v]));
mx = max(mx, res + su - 2 * yzh.query(L[v]) + val[v]);
}
printf("%d\n", mx);
}
}
}
}
\(100 \%\) 部分分
点分树
点击查看代码
namespace ACcode1 {
const int lgN = __lg(N) + 1;
int siz[N], tot, root;
int FA[N], L[N][lgN], R[N][lgN];
int rtdpt[N], key[N];
bool mark[N];
int dpt[N];
void dfs(int now, int fa) {
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa) continue;
dpt[to] = dpt[now] + 1;
dfs(to, now);
}
}
void findroot(int now, int fa) {
siz[now] = 1;
int mx = 0;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa || mark[to]) continue;
findroot(to, now);
siz[now] += siz[to];
mx = max(mx, siz[to]);
}
mx = max(mx, tot - siz[now]);
if (mx <= tot / 2) root = now;
}
void calc(int, int);
void solve(int now, int dpt) {
mark[now] = 1, findroot(now, 0), calc(now, dpt);
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (mark[to]) continue;
tot = siz[to], findroot(to, now);
FA[root] = now;
key[root] = to;
solve(root, dpt + 1);
}
}
int timer, tdfn[N], initdis[N];
struct Segment_Tree {
struct node {
int lson, rson;
int mx, lazy;
} tree[N * lgN * 20];
int tot, root[N];
#define lson tree[idx].lson
#define rson tree[idx].rson
void pushtag(int idx, int v) {
tree[idx].mx += v;
tree[idx].lazy += v;
}
void pushdown(int idx) {
if (tree[idx].lazy == 0) return;
pushtag(lson, tree[idx].lazy);
pushtag(rson, tree[idx].lazy);
tree[idx].lazy = 0;
}
void pushup(int idx) {
tree[idx].mx = max(tree[lson].mx, tree[rson].mx);
}
void build(int &idx, int trl, int trr, int cent) {
idx = ++tot;
if (trl == trr) return pushtag(idx, initdis[tdfn[trl]]);
int mid = (trl + trr) >> 1;
build(lson, trl, mid, cent);
build(rson, mid + 1, trr, cent);
pushup(idx);
}
void modify(int idx, int trl, int trr, int l, int r, int val) {
if (trl > r || trr < l) return;
if (l <= trl && trr <= r) return pushtag(idx, val);
int mid = (trl + trr) >> 1;
pushdown(idx);
modify(lson, trl, mid, l, r, val);
modify(rson, mid + 1, trr, l, r, val);
pushup(idx);
}
int query(int idx, int trl, int trr, int l, int r) {
if (trl > r || trr < l) return -0x3f3f3f3f;
if (l <= trl && trr <= r) return tree[idx].mx;
int mid = (trl + trr) >> 1;
pushdown(idx);
return max(query(lson, trl, mid, l, r), query(rson, mid + 1, trr, l, r));
}
void output(int idx, int trl, int trr) {
if (trl == trr) {
cout << tree[idx].mx << ' ';
return;
}
int mid = (trl + trr) >> 1;
pushdown(idx);
output(lson, trl, mid);
output(rson, mid + 1, trr);
}
#undef lson
#undef rson
} yzh;
void dfs(int now, int fa, int dpt) {
L[now][dpt] = ++timer;
tdfn[timer] = now;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (mark[to] || to == fa) continue;
initdis[to] = initdis[now] + val[to];
dfs(to, now, dpt);
}
R[now][dpt] = timer;
}
void calc(int now, int dpt) {
timer = 0;
L[now][dpt] = ++timer;
tdfn[timer] = now;
initdis[now] = 0;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (mark[to]) continue;
initdis[to] = initdis[now] + val[to];
dfs(to, now, dpt);
}
R[now][dpt] = timer;
rtdpt[now] = dpt;
yzh.build(yzh.root[now], 1, timer, now);
}
void update(int u, int w) {
for (int v = FA[u]; v; v = FA[v]) {
int d = rtdpt[v];
yzh.modify(yzh.root[v], 1, R[v][d], L[u][d], R[u][d], w);
}
}
int query(int u) {
int ans = yzh.query(yzh.root[u], 1, R[u][rtdpt[u]], 1, R[u][rtdpt[u]]) + val[u];
for (int v = FA[u], lst = u; v; lst = v, v = FA[v]) {
int d = rtdpt[v];
int res = 0;
if (L[key[lst]][d] > L[v][d]) res = max(res, yzh.query(yzh.root[v], 1, R[v][d], L[v][d], L[key[lst]][d] - 1));
if (R[key[lst]][d] < R[v][d]) res = max(res, yzh.query(yzh.root[v], 1, R[v][d], R[key[lst]][d] + 1, R[v][d]));
res += val[v] + yzh.query(yzh.root[v], 1, R[v][d], L[u][d], L[u][d]);
ans = max(ans, res);
}
return ans;
}
void solve() {
dfs(1, 0);
tot = n, findroot(1, 0), solve(root, 1);
for (int i = 1; i <= m; ++i) {
int u = qry[i].u, x = qry[i].x;
if (qry[i].op == 1) printf("%d\n", query(u));
else update(u, x - val[u]), val[u] = x;
}
}
}
树链剖分
点击查看代码
namespace ACcode2 {
using pii = pair<int, int>;
set<pii, greater<pii>> st[N];
int L[N], R[N], dfn[N], timer;
int siz[N], top[N], son[N], tail[N], fa[N], dpt[N];
struct Segment_Tree {
#define lson (idx << 1 )
#define rson (idx << 1 | 1)
struct Info {
int lmx, rmx, sum;
inline friend Info operator + (const Info &a, const Info &b) {
return {max(a.lmx, a.sum + b.lmx), max(b.rmx, b.sum + a.rmx), a.sum + b.sum};
}
};
struct node {
int l, r;
Info info;
} tree[N << 2];
inline void pushup(int idx) {
tree[idx].info = tree[lson].info + tree[rson].info;
}
void build(int idx, int l, int r) {
tree[idx].l = l, tree[idx].r = r;
if (l == r) return;
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(idx);
}
void update(int idx, int p) {
if (tree[idx].l > p || tree[idx].r < p) return;
if (tree[idx].l == tree[idx].r) {
tree[idx].info.sum = val[dfn[p]];
tree[idx].info.lmx = tree[idx].info.rmx =
val[dfn[p]] + st[dfn[p]].begin() -> first;
return;
}
update(lson, p), update(rson, p), pushup(idx);
}
Info query(int idx, int l, int r) {
if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].info;
if (r <= tree[lson].r) return query(lson, l, r);
if (l >= tree[rson].l) return query(rson, l, r);
return query(lson, l, r) + query(rson, l, r);
}
#undef lson
#undef rson
} yzh;
using Info = Segment_Tree::Info;
void dfs(int now) {
siz[now] = 1;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa[now]) continue;
fa[to] = now, dpt[to] = dpt[now] + 1;
dfs(to), siz[now] += siz[to];
if (siz[to] > siz[son[now]]) son[now] = to;
}
}
void redfs(int now, int tp) {
st[now].insert({0, now});
dfn[L[now] = ++timer] = now;
tail[top[now] = tp] = now;
if (son[now]) redfs(son[now], tp);
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa[now] || to == son[now]) continue;
redfs(to, to);
Info res = yzh.query(1, L[to], L[tail[to]]);
st[now].insert({res.lmx, to});
}
R[now] = timer;
yzh.update(1, L[now]);
}
inline int query(int u) {
int ans = st[u].begin() -> first + val[u];
for (int sum = val[u]; ; ) {
if (u != tail[top[u]]) {
Info res = yzh.query(1, L[u] + 1, L[tail[top[u]]]);
ans = max(ans, res.lmx + sum);
}
if (u != top[u]) {
Info res = yzh.query(1, L[top[u]], L[u] - 1);
ans = max(ans, res.rmx + sum);
sum += res.sum;
}
if (top[u] == 1) break;
int v = fa[top[u]];
sum += val[v];
auto it = st[v].begin();
if (it -> second == top[u]) it = next(it);
ans = max(ans, sum + it -> first);
u = v;
}
return ans;
}
inline void update(int u, int x) {
val[u] = x;
while (true) {
int v = top[u];
Info lst = yzh.query(1, L[v], L[tail[v]]);
yzh.update(1, L[u]);
Info cur = yzh.query(1, L[v], L[tail[v]]);
if (lst.lmx == cur.lmx || v == 1) break;
st[fa[v]].erase({lst.lmx, v});
st[fa[v]].insert({cur.lmx, v});
u = fa[v];
}
}
void solve() {
dfs(1), yzh.build(1, 1, n), redfs(1, 1);
for (int i = 1; i <= m; ++i) {
int u = qry[i].u, x = qry[i].x;
if (qry[i].op == 1) printf("%d\n", query(u));
else update(u, x);
}
}
}
完整代码
点击查看代码
/*
* Problem link: https://hydro.ac/d/bzoj/p/2158
* My Solution : https://www.cnblogs.com/XuYueming/p/18347278
**/
#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <set>
using namespace std;
#define Hydro
#ifdef XuYueming
# define printf printf(">>>>>>>>> "), printf
#endif
const int N = 100010;
struct Question {
int op, u, x;
} qry[N];
struct Graph {
struct node {
int to, nxt;
} edge[N << 1];
int tot = 1, head[N];
void add(int u, int v) {
edge[++tot] = {v, head[u]};
head[u] = tot;
}
inline node & operator [] (const int x) {
return edge[x];
}
} xym;
int n, m, val[N], eu[N], ev[N];
namespace pts1 {
inline bool check() {
return n <= 1000;
}
int mx;
void dfs(int now, int sum, int fa) {
mx = max(mx, sum);
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa) continue;
dfs(to, sum + val[to], now);
}
}
void solve() {
for (int i = 1; i <= m; ++i) {
if (qry[i].op == 2) {
val[qry[i].u] = qry[i].x;
} else {
mx = -0x3f3f3f3f, dfs(qry[i].u, val[qry[i].u], 0);
printf("%d\n", mx);
}
}
}
}
namespace pts2 {
inline bool check() {
for (int i = 1; i <= n - 1; ++i)
if (eu[i] != i || ev[i] != i + 1)
return false;
return true;
}
struct Segment_Tree {
#define lson (idx << 1 )
#define rson (idx << 1 | 1)
struct node {
int l, r;
int mx, mi;
int lazy;
} tree[N << 2];
void pushtag(int idx, int v) {
tree[idx].lazy += v;
tree[idx].mx += v;
tree[idx].mi += v;
}
void pushdown(int idx) {
if (tree[idx].lazy == 0) return;
pushtag(lson, tree[idx].lazy);
pushtag(rson, tree[idx].lazy);
tree[idx].lazy = 0;
}
inline void pushup(int idx) {
tree[idx].mx = max(tree[lson].mx, tree[rson].mx);
tree[idx].mi = min(tree[lson].mi, tree[rson].mi);
}
void build(int idx, int l, int r) {
tree[idx].l = l, tree[idx].r = r;
if (l == r) return pushtag(idx, val[l]);
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(idx);
}
void modify(int idx, int l, int r, int v) {
if (tree[idx].l > r || tree[idx].r < l) return;
if (l <= tree[idx].l && tree[idx].r <= r) return pushtag(idx, v);
pushdown(idx);
modify(lson, l, r, v);
modify(rson, l, r, v);
pushup(idx);
}
int querymi(int idx, int l, int r) {
if (tree[idx].l > r || tree[idx].r < l) return 0x3f3f3f3f;
if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].mi;
return pushdown(idx), min(querymi(lson, l, r), querymi(rson, l, r));
}
int querymx(int idx, int l, int r) {
if (tree[idx].l > r || tree[idx].r < l) return -0x3f3f3f3f;
if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].mx;
return pushdown(idx), max(querymx(lson, l, r), querymx(rson, l, r));
}
int query(int p) {
return querymi(1, p, p);
}
#undef lson
#undef rson
} yzh;
int tmp[N];
void solve() {
for (int i = 1; i <= n; ++i) tmp[i] = val[i], val[i] += val[i - 1];
yzh.build(1, 0, n);
for (int i = 1; i <= m; ++i) {
int u = qry[i].u, x = qry[i].x;
if (qry[i].op == 2) {
yzh.modify(1, u, n, x - tmp[u]);
tmp[u] = x;
} else {
int mx = -0x3f3f3f3f;
mx = max(mx, yzh.query(u) - yzh.querymi(1, 0, u - 1));
if (u + 1 <= n)
mx = max(mx, yzh.querymx(1, u + 1, n) - yzh.query(u - 1));
printf("%d\n", mx);
}
}
}
}
namespace pts3 {
int mxdpt;
void dfs(int now, int fa) {
static int dpt[N];
mxdpt = max(mxdpt, dpt[now]);
if (dpt[now] > 40) return;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa) continue;
dpt[to] = dpt[now] + 1, dfs(to, now);
if (mxdpt > 40) return;
}
}
inline bool check() {
return dfs(1, 0), mxdpt <= 40;
}
struct Segment_Tree {
#define lson (idx << 1 )
#define rson (idx << 1 | 1)
struct node {
int l, r;
int mx, lazy;
} tree[N << 2];
void pushtag(int idx, int v) {
tree[idx].lazy += v;
tree[idx].mx += v;
}
void pushdown(int idx) {
if (tree[idx].lazy == 0) return;
pushtag(lson, tree[idx].lazy);
pushtag(rson, tree[idx].lazy);
tree[idx].lazy = 0;
}
inline void pushup(int idx) {
tree[idx].mx = max(tree[lson].mx, tree[rson].mx);
}
void build(int idx, int l, int r) {
tree[idx].l = l, tree[idx].r = r;
if (l == r) return;
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(idx);
}
void modify(int idx, int l, int r, int v) {
if (tree[idx].l > r || tree[idx].r < l) return;
if (l <= tree[idx].l && tree[idx].r <= r) return pushtag(idx, v);
pushdown(idx);
modify(lson, l, r, v);
modify(rson, l, r, v);
pushup(idx);
}
int query(int idx, int l, int r) {
if (tree[idx].l > r || tree[idx].r < l) return -0x3f3f3f3f;
if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].mx;
return pushdown(idx), max(query(lson, l, r), query(rson, l, r));
}
int query(int p) {
return query(1, p, p);
}
#undef lson
#undef rson
} yzh;
int fa[N], L[N], R[N], timer;
void dfs(int now) {
L[now] = ++timer;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa[now]) continue;
fa[to] = now;
dfs(to);
}
R[now] = timer;
yzh.modify(1, L[now], R[now], val[now]);
}
int root, siz[N];
void findroot(int now, int fa) {
siz[now] = 1;
int mx = 0;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa) continue;
findroot(to, now);
siz[now] += siz[to];
mx = max(mx, siz[to]);
}
mx = max(mx, n - siz[now]);
if (mx <= n / 2) root = now;
}
void solve() {
yzh.build(1, 1, n), findroot(1, 0), dfs(root);
for (int i = 1; i <= m; ++i) {
int u = qry[i].u, x = qry[i].x;
if (qry[i].op == 2) {
yzh.modify(1, L[u], R[u], x - val[u]);
val[u] = x;
} else {
int su = yzh.query(L[u]);
int mx = val[u] + yzh.query(1, L[u], R[u]) - su;
for (int lst = u, v = fa[u]; v; lst = v, v = fa[v]) {
// L[v]~R[v] L[lst]~R[lst]
int res = -0x3f3f3f3f;
if (L[v] < L[lst]) res = max(res, yzh.query(1, L[v], L[lst] - 1));
if (R[v] > R[lst]) res = max(res, yzh.query(1, R[lst] + 1, R[v]));
mx = max(mx, res + su - 2 * yzh.query(L[v]) + val[v]);
}
printf("%d\n", mx);
}
}
}
}
namespace ACcode1 {
const int lgN = __lg(N) + 1;
int siz[N], tot, root;
int FA[N], L[N][lgN], R[N][lgN];
int rtdpt[N], key[N];
bool mark[N];
int dpt[N];
void dfs(int now, int fa) {
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa) continue;
dpt[to] = dpt[now] + 1;
dfs(to, now);
}
}
void findroot(int now, int fa) {
siz[now] = 1;
int mx = 0;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa || mark[to]) continue;
findroot(to, now);
siz[now] += siz[to];
mx = max(mx, siz[to]);
}
mx = max(mx, tot - siz[now]);
if (mx <= tot / 2) root = now;
}
void calc(int, int);
void solve(int now, int dpt) {
mark[now] = 1, findroot(now, 0), calc(now, dpt);
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (mark[to]) continue;
tot = siz[to], findroot(to, now);
FA[root] = now;
key[root] = to;
solve(root, dpt + 1);
}
}
int timer, tdfn[N], initdis[N];
struct Segment_Tree {
struct node {
int lson, rson;
int mx, lazy;
} tree[N * lgN * 20];
int tot, root[N];
#define lson tree[idx].lson
#define rson tree[idx].rson
void pushtag(int idx, int v) {
tree[idx].mx += v;
tree[idx].lazy += v;
}
void pushdown(int idx) {
if (tree[idx].lazy == 0) return;
pushtag(lson, tree[idx].lazy);
pushtag(rson, tree[idx].lazy);
tree[idx].lazy = 0;
}
void pushup(int idx) {
tree[idx].mx = max(tree[lson].mx, tree[rson].mx);
}
void build(int &idx, int trl, int trr, int cent) {
idx = ++tot;
if (trl == trr) return pushtag(idx, initdis[tdfn[trl]]);
int mid = (trl + trr) >> 1;
build(lson, trl, mid, cent);
build(rson, mid + 1, trr, cent);
pushup(idx);
}
void modify(int idx, int trl, int trr, int l, int r, int val) {
if (trl > r || trr < l) return;
if (l <= trl && trr <= r) return pushtag(idx, val);
int mid = (trl + trr) >> 1;
pushdown(idx);
modify(lson, trl, mid, l, r, val);
modify(rson, mid + 1, trr, l, r, val);
pushup(idx);
}
int query(int idx, int trl, int trr, int l, int r) {
if (trl > r || trr < l) return -0x3f3f3f3f;
if (l <= trl && trr <= r) return tree[idx].mx;
int mid = (trl + trr) >> 1;
pushdown(idx);
return max(query(lson, trl, mid, l, r), query(rson, mid + 1, trr, l, r));
}
void output(int idx, int trl, int trr) {
if (trl == trr) {
cout << tree[idx].mx << ' ';
return;
}
int mid = (trl + trr) >> 1;
pushdown(idx);
output(lson, trl, mid);
output(rson, mid + 1, trr);
}
#undef lson
#undef rson
} yzh;
void dfs(int now, int fa, int dpt) {
L[now][dpt] = ++timer;
tdfn[timer] = now;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (mark[to] || to == fa) continue;
initdis[to] = initdis[now] + val[to];
dfs(to, now, dpt);
}
R[now][dpt] = timer;
}
void calc(int now, int dpt) {
timer = 0;
L[now][dpt] = ++timer;
tdfn[timer] = now;
initdis[now] = 0;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (mark[to]) continue;
initdis[to] = initdis[now] + val[to];
dfs(to, now, dpt);
}
R[now][dpt] = timer;
rtdpt[now] = dpt;
yzh.build(yzh.root[now], 1, timer, now);
}
void update(int u, int w) {
for (int v = FA[u]; v; v = FA[v]) {
int d = rtdpt[v];
yzh.modify(yzh.root[v], 1, R[v][d], L[u][d], R[u][d], w);
}
}
int query(int u) {
int ans = yzh.query(yzh.root[u], 1, R[u][rtdpt[u]], 1, R[u][rtdpt[u]]) + val[u];
for (int v = FA[u], lst = u; v; lst = v, v = FA[v]) {
int d = rtdpt[v];
int res = 0;
if (L[key[lst]][d] > L[v][d]) res = max(res, yzh.query(yzh.root[v], 1, R[v][d], L[v][d], L[key[lst]][d] - 1));
if (R[key[lst]][d] < R[v][d]) res = max(res, yzh.query(yzh.root[v], 1, R[v][d], R[key[lst]][d] + 1, R[v][d]));
res += val[v] + yzh.query(yzh.root[v], 1, R[v][d], L[u][d], L[u][d]);
ans = max(ans, res);
}
return ans;
}
void solve() {
dfs(1, 0);
tot = n, findroot(1, 0), solve(root, 1);
for (int i = 1; i <= m; ++i) {
int u = qry[i].u, x = qry[i].x;
if (qry[i].op == 1) printf("%d\n", query(u));
else update(u, x - val[u]), val[u] = x;
}
}
}
namespace ACcode2 {
using pii = pair<int, int>;
set<pii, greater<pii>> st[N];
int L[N], R[N], dfn[N], timer;
int siz[N], top[N], son[N], tail[N], fa[N], dpt[N];
struct Segment_Tree {
#define lson (idx << 1 )
#define rson (idx << 1 | 1)
struct Info {
int lmx, rmx, sum;
inline friend Info operator + (const Info &a, const Info &b) {
return {max(a.lmx, a.sum + b.lmx), max(b.rmx, b.sum + a.rmx), a.sum + b.sum};
}
};
struct node {
int l, r;
Info info;
} tree[N << 2];
inline void pushup(int idx) {
tree[idx].info = tree[lson].info + tree[rson].info;
}
void build(int idx, int l, int r) {
tree[idx].l = l, tree[idx].r = r;
if (l == r) return;
int mid = (l + r) >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(idx);
}
void update(int idx, int p) {
if (tree[idx].l > p || tree[idx].r < p) return;
if (tree[idx].l == tree[idx].r) {
tree[idx].info.sum = val[dfn[p]];
tree[idx].info.lmx = tree[idx].info.rmx =
val[dfn[p]] + st[dfn[p]].begin() -> first;
return;
}
update(lson, p), update(rson, p), pushup(idx);
}
Info query(int idx, int l, int r) {
if (l <= tree[idx].l && tree[idx].r <= r) return tree[idx].info;
if (r <= tree[lson].r) return query(lson, l, r);
if (l >= tree[rson].l) return query(rson, l, r);
return query(lson, l, r) + query(rson, l, r);
}
#undef lson
#undef rson
} yzh;
using Info = Segment_Tree::Info;
void dfs(int now) {
siz[now] = 1;
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa[now]) continue;
fa[to] = now, dpt[to] = dpt[now] + 1;
dfs(to), siz[now] += siz[to];
if (siz[to] > siz[son[now]]) son[now] = to;
}
}
void redfs(int now, int tp) {
st[now].insert({0, now});
dfn[L[now] = ++timer] = now;
tail[top[now] = tp] = now;
if (son[now]) redfs(son[now], tp);
for (int i = xym.head[now]; i; i = xym[i].nxt) {
int to = xym[i].to;
if (to == fa[now] || to == son[now]) continue;
redfs(to, to);
Info res = yzh.query(1, L[to], L[tail[to]]);
st[now].insert({res.lmx, to});
}
R[now] = timer;
yzh.update(1, L[now]);
}
inline int query(int u) {
int ans = st[u].begin() -> first + val[u];
for (int sum = val[u]; ; ) {
if (u != tail[top[u]]) {
Info res = yzh.query(1, L[u] + 1, L[tail[top[u]]]);
ans = max(ans, res.lmx + sum);
}
if (u != top[u]) {
Info res = yzh.query(1, L[top[u]], L[u] - 1);
ans = max(ans, res.rmx + sum);
sum += res.sum;
}
if (top[u] == 1) break;
int v = fa[top[u]];
sum += val[v];
auto it = st[v].begin();
if (it -> second == top[u]) it = next(it);
ans = max(ans, sum + it -> first);
u = v;
}
return ans;
}
inline void update(int u, int x) {
val[u] = x;
while (true) {
int v = top[u];
Info lst = yzh.query(1, L[v], L[tail[v]]);
yzh.update(1, L[u]);
Info cur = yzh.query(1, L[v], L[tail[v]]);
if (lst.lmx == cur.lmx || v == 1) break;
st[fa[v]].erase({lst.lmx, v});
st[fa[v]].insert({cur.lmx, v});
u = fa[v];
}
}
void solve() {
dfs(1), yzh.build(1, 1, n), redfs(1, 1);
for (int i = 1; i <= m; ++i) {
int u = qry[i].u, x = qry[i].x;
if (qry[i].op == 1) printf("%d\n", query(u));
else update(u, x);
}
}
}
void compressInput() {
int L, now, A, B, Q, tmp;
scanf("%d%d%d%d%d%d%d", &n, &m, &L, &now, &A, &B, &Q), --m;
for (int i = 1; i <= n; ++i) {
now = (now * A + B) % Q, tmp = now % 10000;
now = (now * A + B) % Q;
if (now * 2 < Q) tmp *= -1;
val[i] = tmp;
}
for (int i = 1; i < n; ++i) {
now = (now * A + B) % Q;
tmp = (i < L) ? i : L;
eu[i] = i - now % tmp, ev[i] = i + 1;
xym.add(eu[i], ev[i]), xym.add(ev[i], eu[i]);
}
for (int i = 1; i <= m; ++i) {
now = (now * A + B) % Q;
if (now * 3 < Q) {
now = (now * A + B) % Q;
qry[i].op = 1;
qry[i].u = now % n + 1;
} else {
qry[i].op = 2;
now = (now * A + B) % Q, tmp = now % 10000;
now = (now * A + B) % Q;
if (now * 2 < Q) tmp *= -1;
now = (now * A + B) % Q;
qry[i].u = now % n + 1, qry[i].x = tmp;
}
}
}
void commonInput() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &val[i]);
for (int i = 1; i <= n - 1; ++i) scanf("%d%d", &eu[i], &ev[i]), xym.add(eu[i], ev[i]), xym.add(ev[i], eu[i]);
while (true) {
static char op[10];
scanf("%s", op);
if (*op == 'D') break;
++m;
if (*op == 'Q') {
qry[m].op = 1, scanf("%d", &qry[m].u);
} else {
qry[m].op = 2, scanf("%d%d", &qry[m].u, &qry[m].x);
}
}
}
signed main() {
#ifdef Hydro
char _[2]; scanf("%s", _);
#ifdef XuYueming
commonInput();
#else
compressInput();
#endif
#else
#ifndef XuYueming
freopen("lycoris.in", "r", stdin);
freopen("lycoris.out", "w", stdout);
#endif
commonInput();
#endif
if (pts1::check()) return pts1::solve(), 0;
if (pts2::check()) return pts2::solve(), 0;
if (pts3::check()) return pts3::solve(), 0;
return n & 1 ? ACcode1::solve() : ACcode2::solve(), 0;
}
后记
调点分树调了好久……附上数据生成器以及拍出来的几组数据和图。
数据生成器
#ifdef Hydro
cout << "O" << ' ';
#endif
int n = 10, m = 10, V = 100;
cout << n << endl;
for (int i = 1; i <= n; ++i) cout << rand(-V, V) << ' ';
cout << endl;
for (int i = 2; i <= n; ++i) cout << i << ' ' << rand(1, i - 1) << endl;
while (m--) {
int op = rand(1, 2);
if (op == 1) {
cout << "Change" << ' ' << rand(1, n) << ' ' << rand(-V, V) << endl;
} else {
cout << "Query" << ' ' << rand(1, n) << endl;
}
}
cout << "Done" << endl;
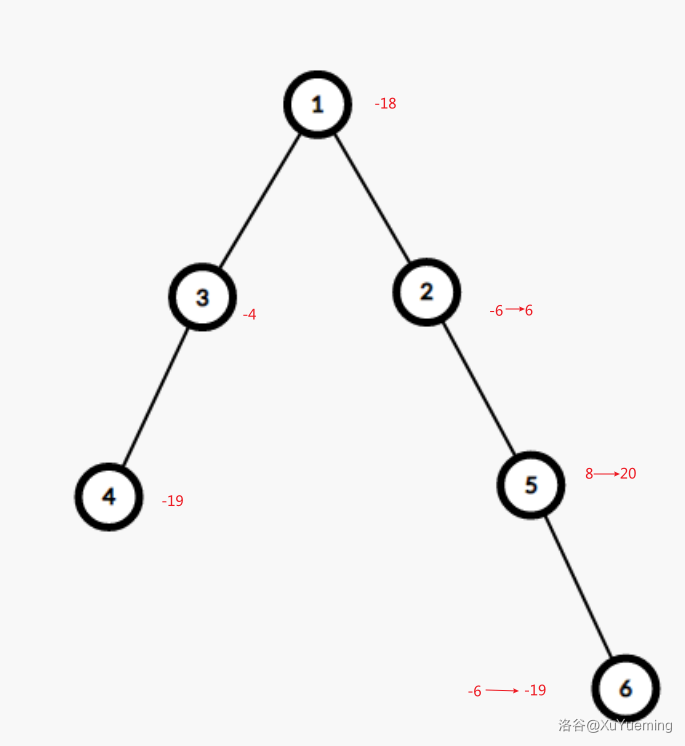
数据 \(1\)
O 6
-18 -6 -4 -19 8 -6
2 1
3 1
4 3
5 2
6 5
Change 6 -19
Change 5 20
Change 2 6
Query 6
Done
数据 \(2\)
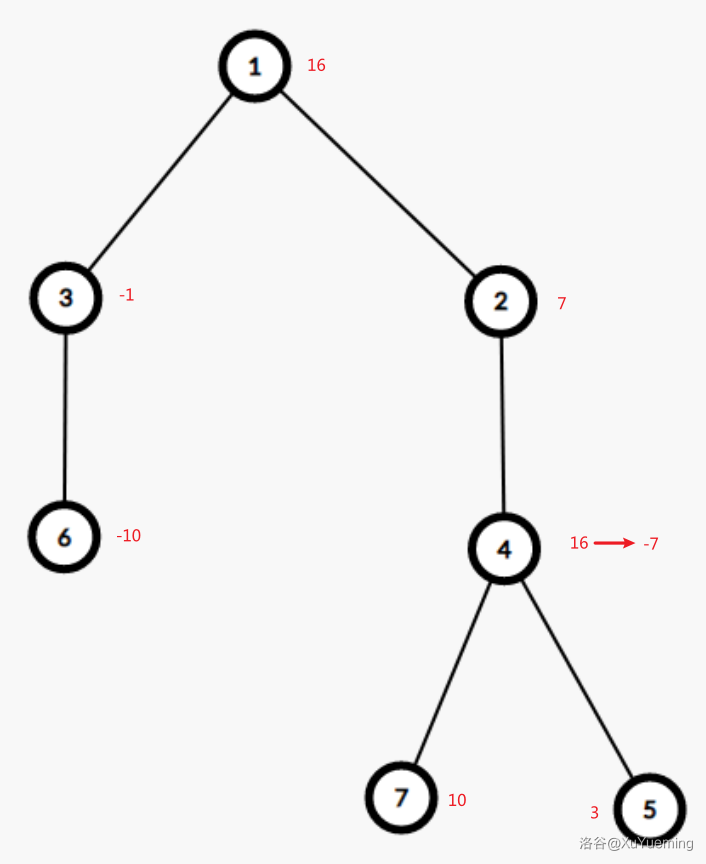
O 7
16 7 -1 16 3 -10 10
2 1
3 1
4 2
5 4
6 3
7 4
Change 4 -7
Query 1
Done
数据 \(3\)
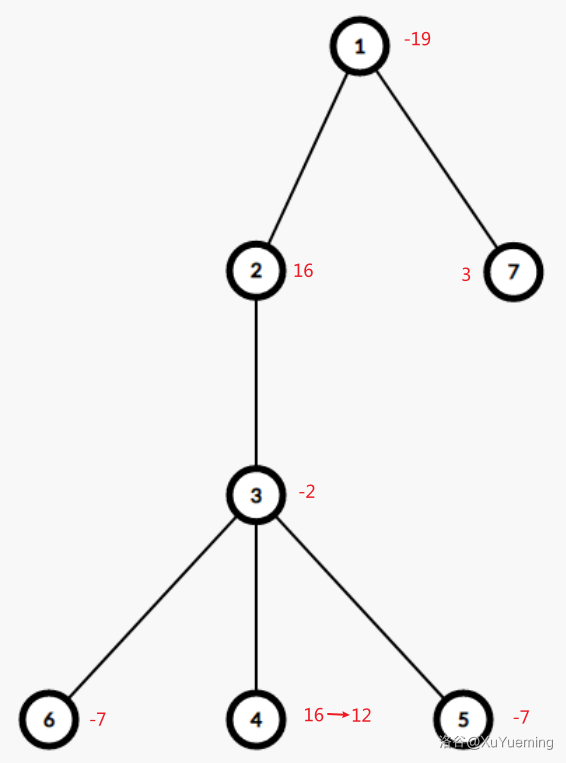
O 7
-19 16 -2 16 -7 -7 3
2 1
3 2
4 3
5 3
6 3
7 1
Change 4 12
Query 2
Done
数据 \(4\)
O 7
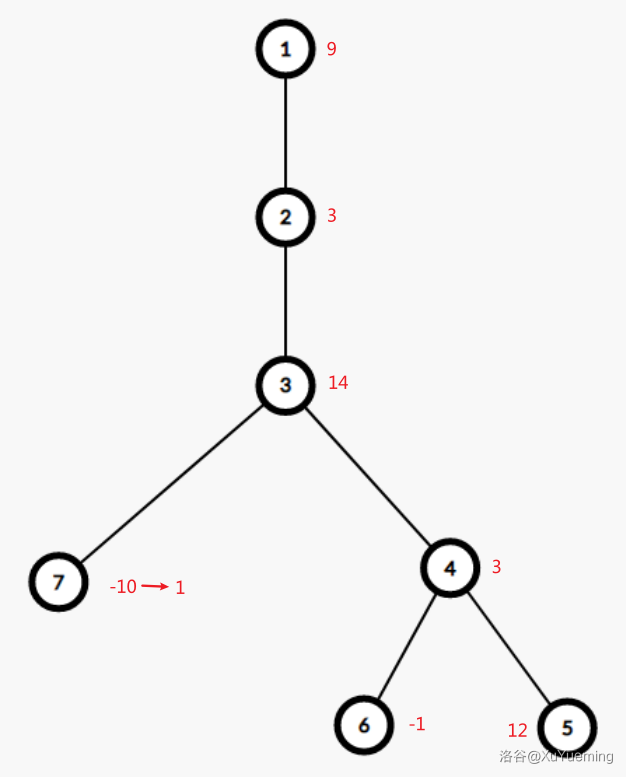
9 3 14 3 12 -1 -10
2 1
3 2
4 3
5 4
6 4
7 3
Change 7 1
Query 1
Done
数据 \(5\)
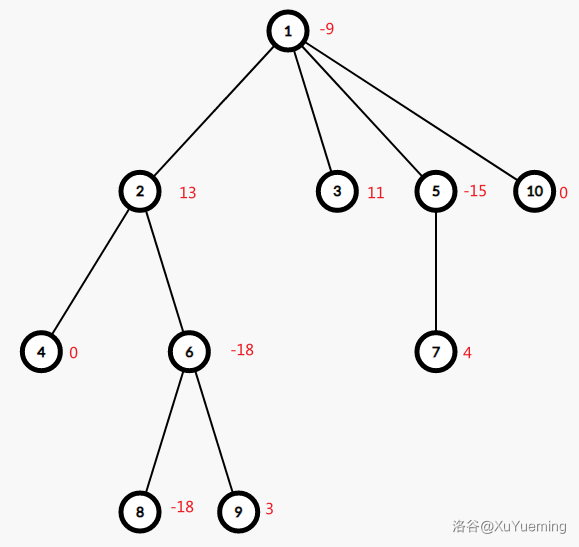
O 10
-9 13 11 0 -15 -18 4 -18 3 0
2 1
3 1
4 2
5 1
6 2
7 5
8 6
9 6
10 1
Query 6
Done
结束了吗?结束了……
标签:Crash,idx,int,题解,彼岸花,yzh,query,now,xym From: https://www.cnblogs.com/XuYueming/p/18347278