标签：right 曼哈顿比雪夫距离理解简单 aligned left

一个蒟蒻对简单距离的简单理解:

呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃呃,写的简单粗暴,如有不对的,欢迎纠正

神马是距离?

在数学中，距离是泛函分析中最基本的概念之一。它所定义的距离空间连接了拓扑空间与赋范线性空间等其他空间，是学习泛函分析首先接触的概念。距离，是指任意二点之间的直线长短。

其实就是一个数学概念

正文

1.简单方面

1-1.欧式距离

1-1-1.介绍

欧式距离是我们在直角坐标系中最常用的距离量算方法

欧氏距离，一般也称作欧几里得距离。在平面直角坐标系中，设点 $A,\ B$ 的坐标分别为 $A(x_1,y_1),B(x_2,y_2)$ ，则两点间的欧氏距离为：

$$
\left | AB \right | = \sqrt{\left ( x_2 - x_1 \right )^2 + \left ( y_2 - y_1 \right )^2}
$$

1-1-2.解释

举个例子，若在平面直角坐标系中，有两点 $A(6,5),B(2,2)$，通过公式，我们很容易得到 $A,B$ 两点间的欧氏距离：

$$
\left | AB \right | = \sqrt{\left ( 2 - 6 \right )^2 + \left ( 2 - 5 \right )^2} = \sqrt{4²⁺³2} = 5
$$

除此之外， P(x,y) 到原点的欧氏距离可以用公式表示为：
$$
|P| = \sqrt{x^2+y2}
$$

1-1-3.例题:

例题有很多,我找了几个:

1-2.曼哈顿距离

1-2-1.公式

观察下图：

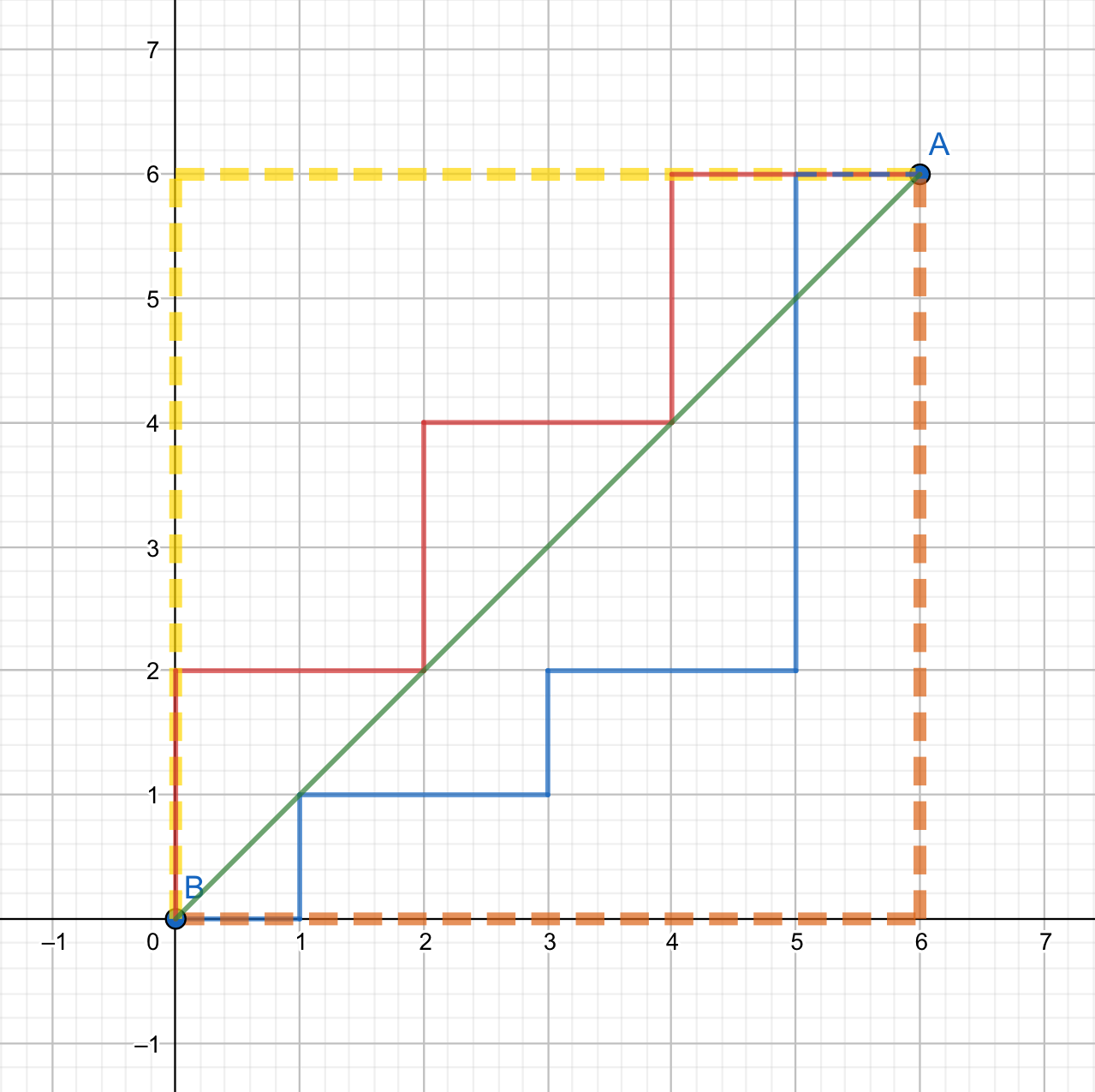
manhattan-dis-diff

在 A,B 间，黄线、橙线都表示曼哈顿距离，而红线、蓝线表示等价的曼哈顿距离，绿线表示欧氏距离。

同样的例子，在下图中 A,B 的坐标分别为 A(25,20),B(10,10) 。

manhattan-dis

通过公式，我们很容易得到 A,B 两点间的曼哈顿距离：
$$
d(A,B) = |20 - 10| + |25 - 10| = 10 + 15 = 25
$$

经过推导，我们得到维空间的曼哈顿距离公式为：
$$
\begin{aligned} d(A,B) &= |x_1 - y_1| + |x_2 - y_2| + \cdot \cdot \cdot + |x_n - y_n|\ &= \sum_{i = 1}^{n}|x_i - y_i| \end{aligned}
$$

除了公式之外，曼哈顿距离还具有以下数学性质：

非负性

曼哈顿距离是一个非负数。
$$
d(i,j)\geq 0
$$
统一性

点到自身的曼哈顿距离为 $0$。
$$
d(i,i) = 0
$$
对称性

$A$ 到 $B$ 与 $B$ 到 $A$ 的曼哈顿距离相等，且是对称函数。
$$
d(i,j) = d(j,i)
$$
三角不等式

从点 $i$ 到 $j$ 的直接距离不会大于途经的任何其它点 $k$ 的距离。
$$
d(i,j)\leq d(i,k)+d(k,j)
$$

1-2-3例题:

P5098「USACO04OPEN」Cave Cows 3

2.中等

2-1.欧式距离(但是是三维)

那么，三维空间中两点的欧氏距离公式呢？我们来观察下图。

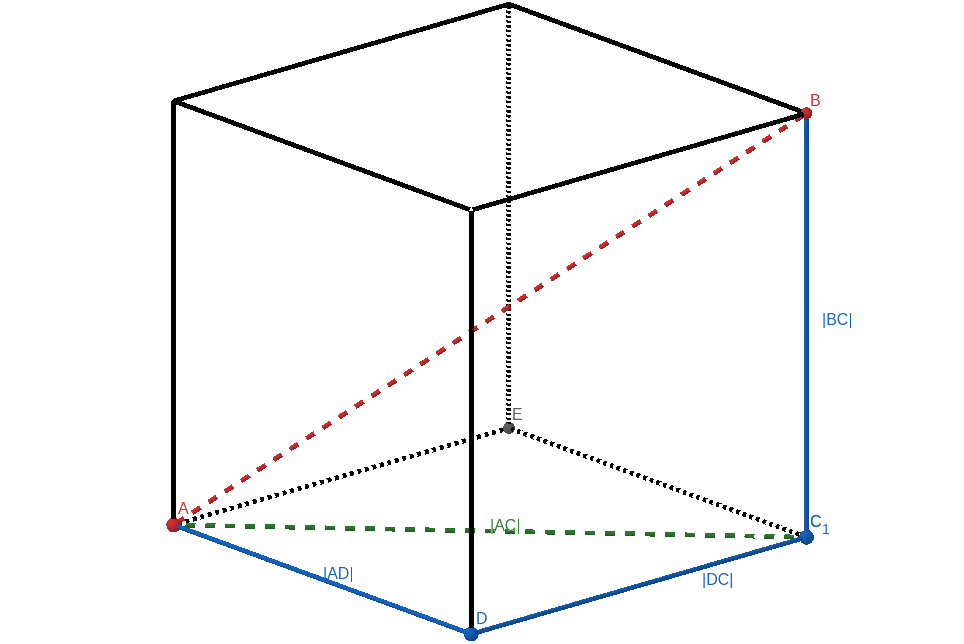
dis-3-dimensional

我们很容易发现，在 $\triangle ADC$ 中，$\angle ADC = 90^\circ$；在 $\triangle ACB$ 中，$\angle ACB = 90^\circ$ 。
$$
\begin{aligned} \therefore ~ |AB| &= \sqrt{|AC|^2+|BC|2} \ &= \sqrt{|AD|^2+|CD|2+|BC|^2} \end{aligned}
$$

2-1-1.定义

由此可得，三维空间中欧氏距离的距离公式为：

$$
\begin{gathered} \left | AB \right | = \sqrt{\left ( x_2 - x_1 \right )^2 + \left ( y_2 - y_1 \right )^2 + \left ( z_2 - z_1 \right )^2} \ |P| = \sqrt{x^2+y2+z^2} \end{gathered}
$$

2-1-2.例题:

NOIP2017 提高组奶酪

2-2.切比雪夫距离

2-2-1.定义

切比雪夫距离（Chebyshev distance）是向量空间中的一种度量，二个点之间的距离定义为其各坐标数值差的最大值。

在二维空间内，两个点之间的切比雪夫距离为它们横坐标之差的绝对值与纵坐标之差的绝对值的最大值。设点 $A(x_1,y_1),B(x_2,y_2)$，则 $A,B$ 之间的切比雪夫距离用公式可以表示为：

$$
d(A,B) = \max(|x_1 - x_2|, |y_1 - y_2|)
$$

$n$ 维空间中切比雪夫距离的距离公式可以表示为：

$$
\begin{aligned} d(x,y) &= \max\begin{Bmatrix} |x_1 - y_1|,|x_2 - y_2|,\cdot \cdot \cdot,|x_n - y_n|\end{Bmatrix} \ &= \max\begin{Bmatrix} |x_i - y_i|\end{Bmatrix}(i \in [1, n])\end{aligned}
$$

2-2-2.解释

仍然是这个例子，下图中 $A,B$ 的坐标分别为 $A(25,20),B(10,10)$

Chebyshev-dis

$$
d(A,B) = \max(|20 - 10|, |25 - 10|) = \max(10, 15) = 15
$$

3.难(nan!)

3-1曼哈顿距离与切比雪夫距离的相互转化

3-1-1过程

首先，我们考虑画出平面直角坐标系上所有到原点的曼哈顿距离为 $1$ 的点。

通过公式，我们很容易得到方程 $|x| + |y| = 1$。

将绝对值展开，得到 $4$ 个一次函数，分别是：
$$
\begin{aligned} &y = -x + 1 &(x \geq 0, y \geq 0) \ &y = x + 1 &(x \leq 0, y \geq 0) \ &y = x - 1 &(x \geq 0, y \leq 0) \ &y = -x - 1 &(x \leq 0, y \leq 0) \ \end{aligned}
$$

将这 $4$ 个函数画到平面直角坐标系上，得到一个边长为 $\sqrt{2}$ 的正方形，如下图所示：

dis-diff-square-1

正方形边界上所有的点到原点的曼哈顿距离都是 $1$。

同理，我们再考虑画出平面直角坐标系上所有到原点的切比雪夫距离为 $1$ 的点。

通过公式，我们知道 $\max(|x|,|y|)=1$。

我们将式子展开，也同样可以得到可以得到 $4$ 条线段，分别是：
$$
\begin{aligned} &y = 1&(-1\leq x \leq 1) \ &y = -1&(-1\leq x \leq 1) \ &x = 1,&(-1\leq y \leq 1) \ &x = -1,&(-1\leq y \leq 1) \ \end{aligned}
$$

画到平面直角坐标系上，可以得到一个边长为 $2$ 的正方形，如下图所示：

dis-diff-square-2

正方形边界上所有的点到原点的切比雪夫距离都是 $1$。

将这两幅图对比，我们会神奇地发现：

这 $2$ 个正方形是相似图形。

3-1-2证明

所以，曼哈顿距离与切比雪夫距离之间会不会有联系呢？

接下来我们简略证明一下：

假设 $A(x_1,y_1),B(x_2,y_2)$，

我们把曼哈顿距离中的绝对值拆开，能够得到四个值，这四个值中的最大值是两个非负数之和，即曼哈顿距离。则 $A,B$ 两点的曼哈顿距离为：
$$
\begin{aligned} d(A,B)&=|x_1 - x_2| + |y_1 - y_2|\ &=\max\begin{Bmatrix} x_1 - x_2 + y_1 - y_2, x_1 - x_2 + y_2 - y_1,x_2 - x_1 + y_1 - y_2, x_2 - x_1 + y_2 - y_1\end{Bmatrix}\ &= \max(|(x_1 + y_1) - (x_2 + y_2)|, |(x_1 - y_1) - (x_2 - y_2)|) \end{aligned}
$$

我们很容易发现，这就是 $(x_1 + y_1,x_1 - y_1), (x_2 + y_2,x_2 - y_2)$ 两点之间的切比雪夫距离。

所以将每一个点 $(x,y)$ 转化为 $(x + y, x - y)$，新坐标系下的切比雪夫距离即为原坐标系下的曼哈顿距离。

同理，$A,B$ 两点的切比雪夫距离为：
$$
\begin{aligned} d(A,B)&=\max\begin{Bmatrix} |x_1 - x_2|,|y_1 - y_2|\end{Bmatrix}\ &=\max\begin{Bmatrix} \left|\dfrac{x_1 + y_1}{2}-\dfrac{x_2 + y_2}{2}\right|+\left|\dfrac{x_1 - y_1}{2}-\dfrac{x_2 - y_2}{2}\right|\end{Bmatrix} \end{aligned}
$$

而这就是 $(\dfrac{x_1 + y_1}{2},\dfrac{x_1 - y_1}{2}), (\dfrac{x_2 + y_2}{2},\dfrac{x_2 - y_2}{2})$ 两点之间的曼哈顿距离。

所以将每一个点 $(x,y)$ 转化为 $(\dfrac{x + y}{2},\dfrac{x - y}{2})$，新坐标系下的曼哈顿距离即为原坐标系下的切比雪夫距离。

3-1-3结论

曼哈顿坐标系是通过切比雪夫坐标系旋转 $45^\circ$ 后，再缩小到原来的一半得到的。
将一个点 $(x,y)$ 的坐标变为 $(x + y, x - y)$ 后，原坐标系中的曼哈顿距离等于新坐标系中的切比雪夫距离。
将一个点 $(x,y)$ 的坐标变为 $(\dfrac{x + y}{2},\dfrac{x - y}{2})$ 后，原坐标系中的切比雪夫距离等于新坐标系中的曼哈顿距离。

碰到求切比雪夫距离或曼哈顿距离的题目时，我们往往可以相互转化来求解。两种距离在不同的题目中有不同的优缺点，应该灵活运用。

3-1-4例题

P4648「IOI2007」pairs 动物对数（曼哈顿距离转切比雪夫距离）

P3964「TJOI2013」松鼠聚会（切比雪夫距离转曼哈顿距离）

4.暂未评定

4-1闵可夫斯基距离

我们定义 $n$ 维空间中两点 $X(x_1, x_2, \dots, x_n)$，$Y(y_1, y_2, \dots, y_n)$ 之间的闵可夫斯基距离为：
$$
D(X, Y) = \left(\sum_{i=1}^n \left\vert x_i - y_i \right\vert ^p\right){p}}.
$$

特别的：

当 $p=1$ 时，$D(X, Y) = \sum_{i=1}^n \left\vert x_i - y_i \right\vert$ 即为曼哈顿距离；
当 $p=2$ 时，$D(X, Y) = \left(\sum_{i=1}^n (x_i - y_i)^2\right)$ 即为欧几里得距离；
当 $p \to \infty$ 时，$D(X, Y) = \lim_{p \to \infty}\left(\sum_{i=1}^n \left\vert x_i - y_i \right\vert ^p\right) ^{1/p} = \max\limits_{i=1}^n \left\vert x_i - y_i \right\vert$ 即为切比雪夫距离。

注意：当 $p \ge 1$ 时，闵可夫斯基距离才是度量，具体证明参见 Minkowski distance - Wikipedia。

4-2汉明距离

汉明距离是两个字符串之间的距离，它表示两个长度相同的字符串对应位字符不同的数量

我们可以简单的认为对两个串进行异或运算，结果为 $1$ 的数量就是两个串的汉明距离。

The End

鸣谢:

OI Wiki
百度

距离大全

标签：right,曼哈顿,比雪夫,距离,理解,简单,aligned,left
From： https://www.cnblogs.com/zzy-hhh/p/18346103

一个蒟蒻对简单距离的简单理解