题目传送门
看到这道题很多人用单调栈,其实用笛卡尔树本质差不多,但是思维难度更小。
简单说来,笛卡尔树的一个子树可以代表一个区间,且左子树上点的下标小于根节点,右子树上点的坐标大于根节点。
这道题要求所有子区间的 \(\texttt{min}\) 值之和,其实就是看哪些子区间的最小值是同一个数,然后计算贡献,所以可以转换成一个树上问题。
我们先根据原序列建出一棵小根堆性质的笛卡尔树(注意树中存的是原序列的下标),这样根节点对应到原序列的值就是子树中的最小值了。
又由于上述性质,设当前根节点为 \(u\),左子树大小为 \(size_l\),右子树大小为 \(size_r\),问题其实变成了:求树上每个节点的 \(a[u]\times (size_l + 1)\times (size_r + 1)\) 之和。
为什么是这样呢?举个例子。
序列 \(\{4,1,3,5,2\}\) 建出来的笛卡尔树长这样:
(为了方便观察,这里直接呈现的是对应到序列中的值。)
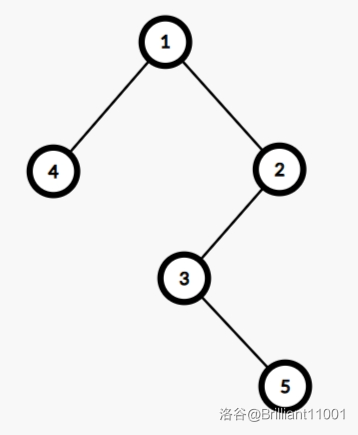
先考虑节点 \(1\),要看有多少个子区间的最小值是它,相当于是看多少对节点的 LCA 是它,根据乘法原理,\(1\) 的贡献就为 \(1\times (1 + 1)\times (3 + 1) = 8\)。事实上确实有 \(8\) 个子区间的最小值是它。
这里 \(+1\) 是因为区间长度可以为 \(1\),也就是只有它自己。
同理,\(4\) 的贡献为 \(4\),\(2\) 的贡献为 \(6\),\(3\) 的贡献为 \(6\),\(5\) 的贡献为 \(5\),加起来总共为 \(29\)。
\(\texttt{Code:}\)
#include <iostream>
using namespace std;
const int N = 200010;
typedef long long ll;
int n;
int a[N];
struct node{
int ls, rs;
}tr[N];
int root;
int stk[N], top;
ll res;
int sz[N];
void build() {
for(int i = 1; i <= n; i++) {
int las = 0;
while(top > 0 && a[stk[top]] >= a[i]) las = stk[top--]; //单调栈优化 O(n) 建树
if(!top) root = i;
if(top) tr[stk[top]].rs = i;
tr[i].ls = las;
stk[++top] = i;
}
}
void dfs(int u) {
sz[u] = 1;
if(tr[u].ls) dfs(tr[u].ls);
if(tr[u].rs) dfs(tr[u].rs);
sz[u] += sz[tr[u].ls] + sz[tr[u].rs];
res += 1ll * a[u] * (sz[tr[u].ls] + 1) * (sz[tr[u].rs] + 1);
}
int main() {
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
build(); //建树
dfs(root); //算贡献
printf("%lld", res);
return 0;
}