进制转换
一个 \(m\) 进制的数字 \(\overline{a_0a_1\cdots a_k}\) 实际上是 \(a_0m^k+a_1m^{k-1}+\cdots+a_k\)。
\(10\) 进制转 \(m\) 进制:每次除以 \(m\) 并取出余数。
\(m\) 进制转 \(10\) 进制:计算 \(a_0m^k+a_1m^{k-}+\cdots+a_k\)。
问题简述:将 \(n\) 进制数转换成 \(m\) 进制数
思路:先转换成 \(10\) 进制,再转换成 \(m\) 进制
std:
#include <iostream>
#include <string>
using namespace std;
int n; //转化前为n进制
int m; //转化后为m进制
int num_10 = 0; //转化成的10进制
string num_n; //转化前的n进制
string num_m; //转化后的m进制
int main(void)
{
cin >> n;
cin >> num_n;
cin >> m;
//n进制转为10进制
int len_n = num_n.length();
for(int i = 0; i < len_n; i++)
{
num_10 *= n;
num_10 += (num_n[i] >= 'A' && num_n[i] <= 'F') ? (num_n[i] - 'A' + 10) : (num_n[i] - '0');
}
while(num_10)
{
num_m = (char)((num_10 % m >= 10) ? (num_10 % m - 10 + 'A') : (num_10 % m + '0')) + num_m;
num_10 /= m;
}
cout << num_m;
return 0;
}
高精度表示
\(\text{int}, \text{long long}\) 分别只能表示 \([−2^31,2^31 ),[−2^63,2^63 )\) 内的数字,超过这个范围就不能用基础数据类型直接表示。
我们可以用一个数组来表示一个高精度数。
例如数组 \([3,2,1]\) 表示十进制下的 \(123\) ,\([3,2,5,1,1]\) 表示 \(11523\) 。(相当于是将数翻转,再拆位)
高精度加减法
与列竖式一样,从低位向高位依次考虑。
做加法时,如果进位,此位 \(−=10\),更高一位 \(+=1\)。
做减法时,如果借位,此位 \(+=10\),更高一位 \(−=1\)。
代码实现:
#include <bits/stdc++.h>
using namespace std;
char a[1005], b[1005];//a,b 两数
int c[1005], d[1005], e[1005];//c是整数形式的a d是整数>形式的b e是和
int main()
{
cin>>a>>b;
int la = strlen(a);//a的长度
int lb = strlen(b);//b的长度
//转整数:
for(int i = 1; i <= la; i++)
{
c[i] = a[i-1] - '0';
}
for(int i = 1; i <= lb; i++)
{
d[i] = b[i-1] - '0';
}
//倒序存放:
reverse(c+1, c+la+1);
reverse(d+1, d+lb+1);
int j = la;
if(j < lb) j = lb;//最大长度
//相加并判断是否进位:
for(int i = 1; i <= j; i++)
{
e[i] += c[i] + d[i];
if(e[i] >= 10)
{
e[i+1]++;
e[i] = e[i] - 10;
}
}
//如果进了一位,说明位数多了一位,j++(位数加一):
if(e[j+1] == 1){
j++;
}
//倒序输出:
for(int i=j;i>=1;i--){
cout<<e[i];
}
return 0;
}
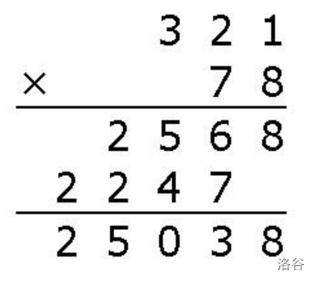
高精度乘法
还是与列竖式类似,逐个数位相乘,最后化简。
如果是 \(A\) 的第 \(i\) 位乘以 \(B\) 的第 \(j\) 位,则实际上指的是 \((A[i]×10^i )×(B[j]×10^j )\),贡献给结果的第 \(i+j\) 位。
复杂度为 \(O(l_A l_B )\)。
代码实现:
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
int c[5005],d[5005],e[10010];
char a[5005],b[5005];
int main(){
scanf("%s%s",a,b);
int la=strlen(a),lb=strlen(b);
for(int i=1;i<=la;i++){
c[i]=a[i-1]-'0';
}
for(int i=1;i<=lb;i++){
d[i]=b[i-1]-'0';
}
reverse(c+1,c+la+1);
reverse(d+1,d+lb+1);
for(int i=1;i<=la;i++){
int x=0;
for(int j=1;j<=lb;j++){
e[i+j-1]=c[i]*d[j]+x+e[i+j-1];
x=e[i+j-1]/10;
e[i+j-1]%=10;
}
e[i+lb]=x;
}
int lc=la+lb;
while(e[lc]==0&&lc>1){
lc--;
}
reverse(e+1,e+lc+1);
for(int i=1;i<=lc;i++)cout<<e[i];
return 0;
}
高精度除以低精度
与竖式除法类似,从高位向低位考虑。
竖式除法每次“带下去”的那个数实际上是目前的余数,这个余数在考虑下一位时位权会 \(×10\)。

pair<vector<int>,int> div(vector<int> A, int B){
vector<int> quotient(A.size());
int remainder =0;
for(int i=A.size()-1;i>=0;i--){
quotient[i]=(A[i]+remainder*10)/ B,
remainder=(A[i]+remainder *10)%B;
while(quotient.back()== 0){
quotient.pop_back();
}
}
return {quotient,remainder};
}
高精度压位
实际上数组每个位置不仅仅可以装一个数位。
例如我们可以让 \([12,34,567]\) 表示 \(7654321\)。
可以限制每个位置装载 \([0,10^9 )\) 的数字。这样两个数字相加不会溢出,但乘法会溢出,需要转为 \(\text{long long}\) 计算。
问题简述:
用高精度计算出 \(S = 1! + 2! + 3! + \cdots + n!\)(\(n \le 50\))。
其中 ! 表示阶乘,定义为 \(n!=n\times (n-1)\times (n-2)\times \cdots \times 1\)。例如,\(5! = 5 \times 4 \times 3 \times 2 \times 1=120\)。
思路:用高精度乘上低精度,每次拿出 \(a_{i-1}\times i\) 即可
std:
#include<iostream>
#include<cstring>
using namespace std;
int n,a[90],b[90],c[90],f[90],d=0,len_a,len_b=1,len_c=1,len_ans,m=1;
string s;
int main(){
cin>>n;
b[0]=1;
for(int i=1;i<=n;i++){
len_a=0;
int p=i;
while(p>0){
a[len_a++]=p%10;
p/=10;
}
for(int j=0;j<len_a;j++)
for(int k=0;k<=len_b;k++)
c[j+k]+=a[j]*b[k];
for(int j=0;j<len_c;j++)
if(c[j]>9) c[j+1]+=c[j]/10,c[j]%=10;
if(c[len_c]) len_c++;
len_ans=len_b,len_b=len_c,m=max(m,len_c);
for(int k=len_c-1;k>=0;k--) b[k]=c[k];
len_c=len_a+len_ans;
memset(c,0,sizeof(c));
for(int j=0;j<m;j++){
f[j]+=b[j];
if(f[j]>9) f[j+1]+=f[j]/10,f[j]%=10;
}
}
while(!f[m]&&m>0) m--;
for(int i=m;i>=0;i--) cout<<f[i];
return 0;
}
组合数学基础
加法原理:做完一件事有 \(n\) 类方法,每类方法有 \(a_i\) 个方法,那么做完这件事有 \(a_1+a_2+…+a_n\) 个方法。
乘法原理:做完一件事有 \(n\) 个步骤,每个步骤有 \(a_i\) 个方法,那么做完这件事有 \(a_1×a_2×…×a_n\) 个方法。
排列数
从 \(n\) 个不同的元素中任取 \(m\) 个元素,按照一定顺序排成一列,其方案数称为 \(A_n^m\)。
\[A_n^m=n(n-1)(n-2)\cdots (n-m+1) = \frac{n!}{(n-m)!} \]第一个位置有 \(n\) 种取法,第二个位置有 \(n−1\) 种取法,第 \(i\) 个位置有 \(n−i+1\) 种取法。
全排列(即 \(m=n\))时,\(A_n^n=n!\)
\[A_n^m=A_{n-1}^m+mA_{n-1}^{m-1} \]考虑第 \(n\) 号元素是否选取。
如果不选取,则需要在前 \(n−1\) 个元素中选取 \(m\) 个排成一列,方案数为 \(A_(n−1)^m\)。
如果选取,则首先需要给 \(n\) 号元素指定一个位置(\(m\) 种可能),然后从前 \(n−1\) 个元素中选取 \(m−1\) 个排成一列。
组合数
从 \(n\) 个不同的元素中任取 \(m\) 个元素,组成一个集合,其方案数称为 \(C_n^m\)。
\(C_n^m\) 与 \(A_n^m\) 的区别在于其不关注选出元素的顺序,只关注选取哪些元素。
每一个大小为 \(m\) 的集合都对应着 \(m!\) 个排列。所以 \(A_n^m=m!C_n^m\)。
所以有
\[C_n^m=\frac{n!}{m!(n-m)!} \]组合数 \(C_n^m\) 又常写作 \(\binom{n}{m}\)。注意 \(n\) 和 \(m\) 上下颠倒了。
\[C_n^m=C_{n-1}^m+C_{n-1}^{m-1} \]同样考虑第 \(n\) 号元素是否选取。
如果不选取,则需要在前 \(n−1\) 个元素中选取 \(m\) 个组成集合,方案数为 \(C_{n-1}^m\)。
如果选取,则需要在前 \(n−1\) 个元素中选取 \(m−1\) 个组成集合。方案数为 \(C_{n-1}^{m-1}\) 。这里我们不需要给第 \(n\) 号元素指定位置。
思路:
用递推式 \(C_n^m=C_{n-1}^m+C_{n-1}^{m-1}\) 计算每个\(C_n^m\mod k\) 的值。
然后使用二维前缀和预处理 \(
标签:24,10,进制,int,day3,len,num,include,集训 From: https://www.cnblogs.com/yantaiyzy2024/p/18340812