如果您是搜索引擎搜进来的。
很抱歉,没有您需要搜索的题目的题解。
典题
\(n\) 个物品的背包,重量在 \(1 \sim 4\) 之间,价值在 \(1 \sim 10^9\) 之间。\(n \leq 10^5\)。
Minkowski 和会遇到不连续的问题。不妨按照 \(i\bmod 12\) 划分 dp 数组,每个剩余系都是凸的。
-
枚举拿了 \(cnt_1\bmod 12\) 个 \(1\),\(cnt_2\bmod 6\) 个 \(2\)……。然后将 \(12\) 个 \(1\),\(6\) 个 \(2\)……绑在一起,贪心。
-
或者分治,一个分治区间维护 \(12\) 个凸函数,逐个合并。
[CF1787H] Codeforces Scoreboard
按照 \(k\) 从大到小排序。如果没有 \(a_i\),则直接按 \(k\) 从大到小做就最优。不妨设 \(dp_{i, j}\) 表示前 \(i\) 题中有 \(j\) 个题不是选的 \(a_i\),有:
\[dp_{i, j}=\max(dp_{i-1, j-1}+b_i-k_ij, dp_{i-1, j}+a_i) \]说可以平衡树维护关于 \(j\) 的凸包。
[ABC305Ex] Shojin
计算区间的代价:先扔掉对答案贡献 \(b_i\) 的 \(a_i=1\) 的函数,那么剩下的函数复合起来增长超快,区间长度必然不会很大。进一步地,可以发现是按照 \(b_i/(a_i-1)\) 从小到大排序。
dp:由上述可知区间长度很小,可以暴力转移;还可以决策单调性,有一个 cdq 将分治决策单调性改到在线的做法,能使用莫队技巧计算区间权值。
还是可以 wqs 二分。有个共线问题,不一定能刚好切到中间。不过可以发现共线部分是一个等差数列,从两边分别逼近就能知道等差数列的两端。
[PA 2022] Nawiasowe podziały
题解 LGP9266【[PA 2022] Nawiasowe podziały】/ SS240121A【Bracket】 - caijianhong - 博客园 (cnblogs.com)
[CF1842I] Tenzing and Necklace
放弃了
DP的决策单调性优化总结 - 洛谷专栏 (luogu.com)
[GYM102268J] Jealous Split
放弃了
[JOISC 2023 Day3] 合唱
洛谷题解写得好啊
GYM102331J
Minkowski 和。然后树剖,对重链分治,或者全局平衡二叉树。
GYM102331H
单次询问又是 Minkowski 和。多次询问在线段树上 \(O(\log n)\) 个区间上 wqs 二分。
好像不是啊
GYM103860I
将题目改完要求最长的形如 \(01010101\cdots\) 的形式,\(k\) 个 \(01\) 可以 \(k\) 次 reverse 计入答案。当然指的都是 \(0/1\) 连续段。Minkowski 和。
LOJ6289 花朵
用动态 DP 的方法大力分治 FFT?
「JOISC 2022 Day1」京都观光
考虑给一个矩形,考察走左下边界和右上边界哪个更好。大概这样:

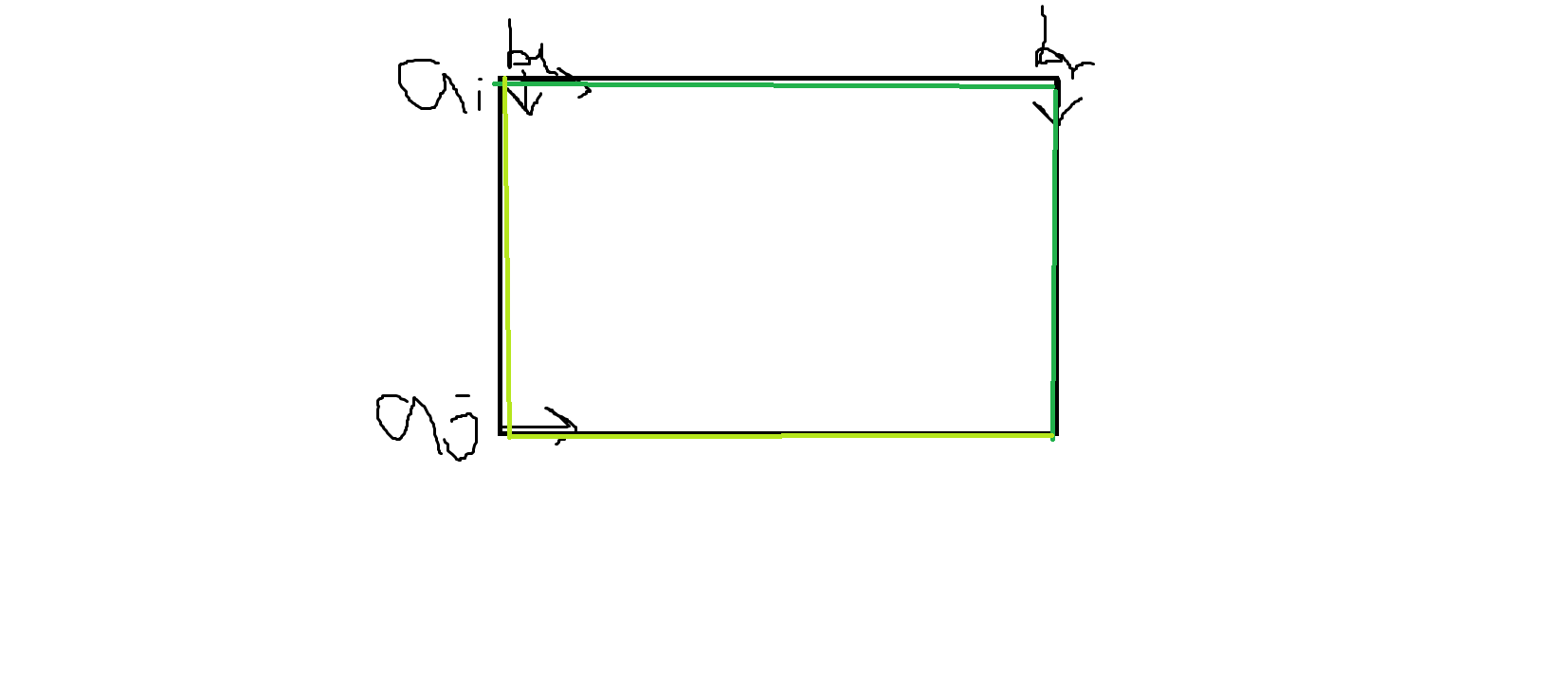
左下优于右上当且仅当:
\[a_j(r-l)+b_l(j-i)<a_i(r-l)+b_r(j-i) \]即
\[\frac{a_j-a_i}{j-i}<\frac{b_r-b_l}{r-l} \]考虑折线情况:

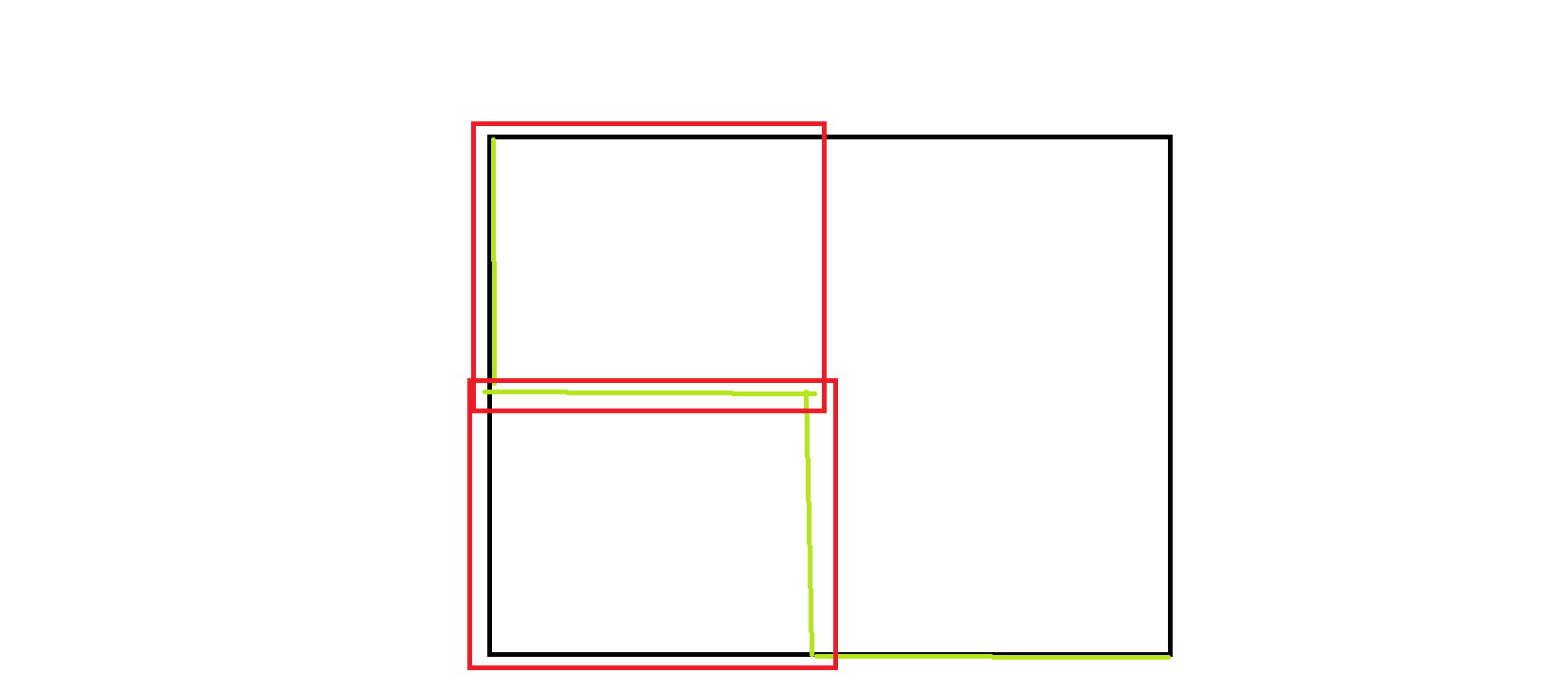
下面一行是 \(k\) 则有:
\[\frac{a_j-a_i}{j-i}<\frac{b_r-b_l}{r-l}\land \frac{a_k-a_j}{k-j}>\frac{b_r-b_l}{r-l} \]\[\frac{a_j-a_i}{j-i}<\frac{a_k-a_j}{k-j} \]看成 \((i, a_i)\) 的点,对两维分别求凸包,然后发现按照斜率顺序走,就是对两个维度的凸包求 Minkowski 和的意思。
「2021 集训队互测」蜘蛛爬树
\[ans=dis(u, v)+a_x\cdot\text{版本号之差}+dis(x, \text{u到v的路径}) \]树剖,对重链分治,维护轻子树构成的凸包,还是做 Minkowski 和。这个只是大致的思路,意思是正确的解法和这个差很多。
[CF1534G] A New Beginning
转曼哈顿。Annie 可以走右上或右下,走到土豆的横坐标上时,曼哈顿距离必然最小(到达前单调不增)。
可以写出 dp 方程了。
Slope trick。
标签:选讲,frac,2024.8,Minkowski,分治,区间,12,大赏,dp From: https://www.cnblogs.com/caijianhong/p/18340704