下午
内容:STL 差分前缀和倍增
1. STL
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <vector>
#include <cstring>
#include <cstdio>
#include <set>
#include <map>
#include <unordered_map>
#include <bitset>
using namespace std;
void text(){
vector<int>v;
vector<int>A(5);
vector<int>B(5,3);
vector<int>C={1,2,3};
for(vector<int>::iterator it=A.begin();it!=A.end();it++)cout<<*it<<" ";
puts("");
for(auto it:B)cout<<it<<" ";
puts("");
for(int i=0;i<(int)C.size();i++)cout<<C[i]<<" ";
puts("");
int n;
cin >> n;
v.resize(100);
cout<<(int)v.size()<<"\n";//unsigned
cout<<(int)v.capacity()<<"\n";
for(int i=1;i<=n;i++)
v.push_back(i);
cout<<(int)v.size()<<"\n";//unsigned
cout<<(int)v.capacity()<<"\n";
v.shrink_to_fit();
cout<<(int)v.capacity()<<"\n";
v.push_back(2);
cout<<(int)v.size()<<"\n";
cout<<(int)v.capacity()<<"\n";
v.clear();
cout<<(int)v.capacity()<<"\n";
vector<int>().swap(v);
cout<<(int)v.capacity()<<"\n";
}
namespace basic
{
basic_string<int>v;
void test()
{
int n;
cin >> n;
v.resize(100);
cout<<(int)v.size()<<"\n";//unsigned
cout<<(int)v.capacity()<<"\n";
for(int i=1;i<=n;i++)
v.push_back(i);
cout<<(int)v.size()<<"\n";//unsigned
cout<<(int)v.capacity()<<"\n";
v.shrink_to_fit();
cout<<(int)v.capacity()<<"\n";
v.push_back(2);
cout<<(int)v.size()<<"\n";
cout<<(int)v.capacity()<<"\n";
v.clear();
cout<<(int)v.capacity()<<"\n";
basic_string<int>().swap(v);
cout<<(int)v.capacity()<<"\n";
basic_string<int>A={2,3,4};
basic_string<int>B={2,3,4};
for(auto it:A)cout<<it<<" ";
puts("");
A=A+B;
for(auto it:A)cout<<it<<" ";
puts("");
//string
cout<<A.find({4,2})<<"\n";
}
}
namespace se
{
set<int>A;
multiset<int>B;//set如果插入重复的元素会自动销毁 , 而multiset不会
void test()
{
for(int i=1;i<=3;i++)
{
A.insert(i);//pair <bool,iterator>
A.insert(i);
B.insert(i);//指针 iterator
B.insert(i);
}
for(auto it:A)cout<<it<<" ";
puts("");
for(auto it:B)cout<<it<<" ";
puts("");
multiset<int>::iterator x=B.lower_bound(0);
multiset<int>::iterator y=B.find(2);
B.erase(x);
for(auto it:B)cout<<it<<" ";
puts("");
B.erase(3);
for(auto it:B)cout<<it<<" ";
puts("");
cout<<(int)B.size()<<"\n";
cout<<(int)B.count(2)<<"\n";
A.clear(),B.clear();
//不能数组下标访问。
}
}
namespace ma
{
map<int,int>A;
unordered_map<int,int>B;
void test()
{
for(int i=1;i<=3;i++)A[i]=i-1,B[i]=i-1;
for(auto it:A)cout<<it.first<<" "<<it.second<<"\n";
puts("");
auto it=A.find(2);//key
cout<<A[4]<<"\n";
A.clear(),B.clear();
}
}
namespace bit
{
bitset<10>bit,bb;
void test()
{
bit[5]=1;
cout<<bit<<"\n";
bit.flip();
bit<<=3;
cout<<bit<<"\n";
bb[1]=1;
bb[4]=1;
cout<<bb<<"\n";
bit^=bb;
cout<<bit<<"\n";
int A=bit._Find_first();
cout<<A<<"\n";
cout<<bit._Find_next(A)<<"\n";
}
}
int main(){
vector<int> a = {1,2,3};
for(auto it:a){
cout << it << " ";
}
text();
basic::test();
basic_string<int>aa = {1, 2, 3};//头文件在iostream
for(auto it:aa){
cout << it << " ";
}
return 0;
}
2. 差分前缀和
不难,可以解决区间问题
std:
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <vector>
#include <cstring>
#include <cstdio>
#include <set>
#include <map>
#include <unordered_map>
#include <bitset>
using namespace std;
const int MAXX = 1e5 + 10;
int a[MAXX], n;
int main(){
cin >> n;
for(int i = 1;i <= n;i++){
int x;
cin >> x;
a[i] = x + a[i - 1];
}
int q;
cin >> q;
while(q--){
int l, r;
cin >> l >> r;
cout << a[r] - a[l - 1] << '\n';
}
return 0;
}
差分
实现:对于每个区间 \([l, r]\),让 \(a_l\) 加上 \(v\),\(a_r+1\) 减去 \(v\)。
最大加权矩形
给定一个 \(n \cdot n\) 的矩形,询问这个矩形内部和最大的一个子子矩形,这个子矩形的和是多少?
\(n ≤ 120\)
std:
const int xx=1005;
int n,q;
ll a[xx][xx];
int main(){
n=read();
for(int i=l;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=read();
ll ma=0;
for(int x=1;x<=n;x++)
for(int y=1;y<=n;y++)
for(int i=x;i<=n;i++)
for(int j=y;j<=n;j++)
ma=max(ma,a[i][j]+a[x-1][y-1]-a[i][y-1]-a[x-1][j]);
cout<<ma<<"\n";
return 0;
}
二维数组前缀和
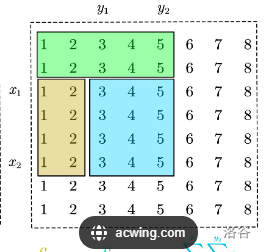
问题简述:
在 \(n\times n\) 的格子上有 \(m\) 个地毯。
给出这些地毯的信息,问每个点被多少个地毯覆盖。
std:
#include <iostream>
#define maxn 1005
int n,m,a[maxn][maxn];
int main(){
std::cin.tie(0)->sync_with_stdio(0);
std::cin >> n >> m;
for (int i = 1;i <= m;i++){
int x1,y1,x2,y2;
std::cin >> x1 >> y1 >> x2 >> y2;
for (int j = x1;j <= x2;j++)
for (int k = y1;k <= y2;k++)
a[j][k]++;
}
for (int i = 1;i <= n;i++){
for (int j = 1;j <= n;j++)
std::cout << a[i][j] << ' ';
std::cout << '\n';
}
return 0;
}
倍增(ST 表)
可解决的问题:区间极值
问题简述:给定一个长度为 \(N\) 的数列,和 $ M $ 次询问,求出每一次询问的区间内数字的最大值。
std:
#include <iostream>
#include <queue>
#include <cmath>
#include <algorithm>
#include <vector>
#include <cstring>
#include <cstdio>
#include <set>
#include <map>
#include <unordered_map>
#include <bitset>
using namespace std;
inline int read(){
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
return x*f;
}
const int MAXN = 100005;
int n, m;
int a[MAXN], f[MAXN][21];
int main(){
n = read(), m = read();
for(int i = 1;i <= n;i++){
a[i] = read();
f[i][0] = a[i];
}
for(int j = 1;j <= 20;j++){
for(int i = 1;i <= n;i++){
if(i + (1 << j) - 1 <= n){
f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}
}
}
while(m--){
int l = read(), r = read();
int k = __lg(r - l + 1);
cout << max(f[l][k], f[r - (1 << k) + 1][k]) << '\n';
}
return 0;
}